Введение
При проведении экологической экспертизы уровня загрязнения окружающей среды, а также для установления степени опасности биологически токсичных веществ важное место занимает биотестирование (англ. bioassay). В то же время, результаты токсикологических испытаний не всегда имеют однозначный характер, поскольку какое-либо вещество, или их смесь, может привести к возникновению специфических реакций у тест-объектов, особенно на клеточном или тканевом уровнях организации. Нередко при исследовании одной и той же пробы в батарее биотестов получаются различные отклики, экспериментальную ценность которых и приемлемость для заключения о токсичности необходимо подтверждать корректными статистическими расчетами (Yakimenko, Terekhova, 2011).
Целью представленной работы было оценить в статистической программе R статистическую значимость и корреляцию значений разных тест-функций в результате проведенных токсикологических экспериментов с одной тест-культурой.
Материалы
Данными служили результаты экспериментов по оценке токсичности образца высокоминерализованных отходов промышленного производства согласно методике ФР.1.39.2009.06596, ПНД Ф Т 16.3.15-09 (Жмур, 2009). Водный экстракт отхода готовили при 7 часовой экстракции в соотношении по массе 1:10 (отход: вода). В эксперименте проанализированы три варианта проб: водный экстракт образца отхода с добавлением питательной среды Гольберга для роста водорослей (исходная проба) и водные разведения исходной пробы – 1 к 50 и 1 к 100. Каждое разведение пробы было представлено в трехкратной повторности. Контролем служила питательная среда Гольдберга. Оценивали две тест-функции: изменение прироста численности клеток и уровня флуоресценции хлорофилла лабораторной культуры морских диатомовых водорослей Phaeodactylum tricornutum за установленный методикой период экспозиции (72 ч).
Численность клеток микроводорослей Ph. tricornutum учитывали при прямом микроскопировании суспензии в камере Горяева. Эксперимент с учетом численности клеток повторяли дважды. Уровень флуоресценции проб измеряли с помощью анализатора Флюорат-02-5М (Lumex, РФ) при возбуждении флуоресценции хлорофилла в диапазоне 400–500 нм и регистрации флуоресценции хлорофилла в диапазоне 650–750 нм. Эксперимент по оценке динамики уровня флуоресценции повторяли трижды.
Традиционные методы исследований
Согласно используемой методике (Жмур, 2009), за результат принимают среднее арифметическое результатов трех параллельных измерений при выполнении условия приемлемости. А именно: диапазон (xmax - xmin) результатов измерений сопоставляют с критическим диапазоном СR0.95(n), рассчитанным для соответствующего значения n по формулам и таблицам, приведенным в ГОСТ Р ИСО 5725-6-2002. Если диапазон результатов не превышает критический, то среднее арифметическое значение результатов всех n измерений принимают за окончательный результат. Подобная схема обработки и оценки результатов применяется и в других методиках биотестирования (Жмур, 2007 и др.). Значения СR0.95, согласно используемой методике по уровню флуоресценции хлорофилла, равен – 23%, по численности клеток – 36%. Критерием острой токсичности признается снижение уровня флуоресценции водорослей или снижение численности клеток водорослей на 50 % и более по сравнению с контролем.
Такой способ оценки острой токсичности по результатам биотестирования сложно признать полностью корректным, так как конкретный вывод, по крайней мере, не основывается на статистической проверке различий и не отражает особенностей шкалы измерения и «статистической эластичности» тест-функции. В частности, для показателей с низким базовым значением и высокой вариабельностью отклонение от нормы в несколько раз может не быть свидетельством токсичности, тогда как для иных тест-функций сдвиг показателя на 10–20% по сравнению с контролем является выраженным сигналом опасного воздействия (Трахтенберг и др., 1991). И хотя в используемой нами методике при указании значений СR0,95 учтена различная вариабельность двух тест-функций, в критерии острой токсичности она не принимается во внимание. Оценка, действительно ли имеет место токсическое действие, должна основываться на общепринятых принципах проверки статистических гипотез.
Оригинальные методы исследований
Необходимым условием современного статистического анализа данных является применение различных компьютерных программ, от функциональной полноты и алгоритмической продуманности которых зависит итоговая интерпретация результатов исследования и правильность выводов. По результатам анализа публикаций биологического профиля нам удалось найти информацию об использовании более 60 прикладных программ, ориентированных на статистическую обработку. Зарубежные авторы чаще всего пользуются Microsoft Excel, SAS и Statview 4.0 (например, Benjamin, Preston, 2002), Statgraphics Centurion (Stefanowicz et al., 2008), SIRIUS (Frostegåd et al., 1993), GenStat, Stata и R (Jennifer et al., 2009). Российские исследователи, как правило, работают с программой Statistica (Timofeyev, Shatilina, 2007), стоимость одной лицензии которой составляет более 85 тыс. руб. В сети Интернет можно найти достаточно полный перечень коммерческих (Comparison…) и бесплатных (Free Statistical…) статистических программ с оценками их аналитических и графических возможностей.
Свободно распространяемая статистическая среда R является одновременно языком программирования высокого уровня и прикладной программой для вычислительной и графической обработки данных (http://www.r-project.org/). Программа позволяет одной строкой реализовать различные операции с объектами, векторами, матрицами, списками и т.д.; содержит большой набор функций обработки данных, собранных в отдельные пакеты (package), и развитую систему поддержки (Venables, Smith, 2014). «Сегодня R является безусловным лидером среди свободно распространяемых систем статистического анализа…» (Маcтицкий, Шитиков, 2015, с.5-6). К недостаткам программы можно отнести ограниченное количество литературы на русском языке, отсутствие системы рассылки об обновлениях и привычного графического интерфейса.
Далее рассматривается расширенная процедура токсикологической оценки образцов высокоминерализованных отходов производства по изменению значений двух тест-функций (численность клеток и интенсивность флуоресценции хлорофилла) с использованием следующих статистических методов:
- проверка статистической значимости токсического воздействия с помощью однофакторного дисперсионного анализа (ANOVA);
- оценка достоверности различий между различными вариантами опыта в ходе множественных сравнений;
- анализ линейной связи между обеими тест-функциями с расчетом коэффициентов корреляции Пирсона и Спирмена.
Все расчеты выполнены в статистической программе R с применением алгоритмов из опубликованных работ (Заряднов, 2010; Шитиков, Мастицкий, 2015; Шипунов, 2014). Перечень всех скриптов, необходимых для расчетов, приведен в Приложении.
Обсуждение
После запуска программы R с консоли вводили данные по численности клеток и уровню флуоресценции водорослей Ph. tricornutum (рис. 1; блок 1 в Приложении).
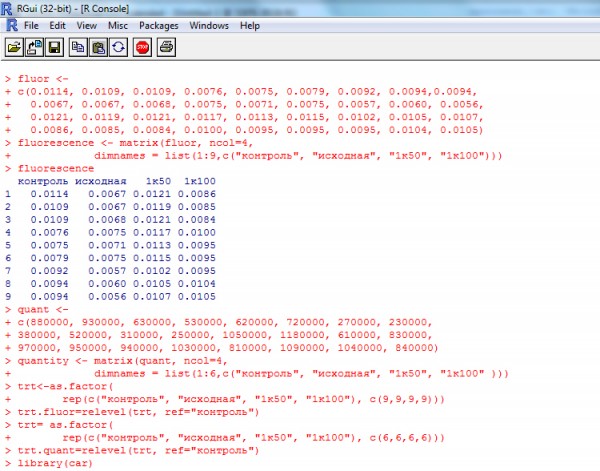
Рис. 1. Иллюстрация расчетов в программе R
Fig.1. Illustration of the calculations in the statistical program R
Затем рассчитывали выборочные параметры описательной статистики (блок 2 в Приложении). Для этого определили собственную процедуру расчета необходимых показателей с использованием функции apply. Средние значения уровня флуоресценции в контрольной, исходной пробах и разведениях 1/50 и 1/100 соответственно равны (усл.ед): 0.0094 ± 0.0005; 0.0066 ± 0.0003; 0.0113 ± 0.0002; 0.0094 ± 0.0003. Средние значения численности водорослей для этих же проб следующие (кол-во клеток/куб.см): 718333.3 ± 64260.8; 326666.7 ± 44322.1; 931666.7 ± 79850.6; 958333.3 ± 46720.2. Альтернативным вариантом расчета параметров описательной статистики является использование функции stat.desc() из пакета pastecs, вычисляющей обширный набор выборочных характеристик, позволяющих получить достаточно полное представление об анализируемых данных.
Результаты экспериментов оценивали согласно критерию острой токсичности, т.е. величина тест-функции в условиях воздействия должно составлять менее 50% от контрольного значения (блок 3 в Приложении).
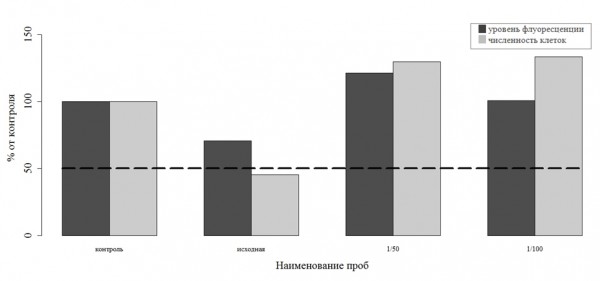
Рис. 2. Сравнение значений изменений численности клеток и интенсивности флуоресценции хлорофилла микроводорослей Ph. tricornutum в эксперименте с разведением проб отхода (% к контролю)
Fig. 2. Comparison of the population changes of cells and intensity of chlorophyll fluorescence of microalgae Ph. tricornutum in the experiment with dilution of waste samples (% to control)
Основываясь на численности клеток водорослей, можно заключить, что проба в исходном состоянии обладает острой токсичностью (45.5% от контроля). В то же время, судя по изменению уровня флуоресценции, такой вывод сделать нельзя (подавление флуоресценции не превысило 50 %-ного уровня) (рис. 2). Для того чтобы сопоставить уровни значимости полученных значений тест-функций, был проведен однофакторный дисперсионный анализ (блок 4 в Приложении). Предварительно проверили, отвечают ли полученные нами данные необходимым условиям анализа, а именно: зависимая переменная Y в каждом варианте опыта распределена нормально (а), дисперсия значений Y одинакова для всех анализируемых групп (б).
При помощи формального теста Шапиро (Shapiro-Wilk normality test) проверили нулевую гипотезу (а): происходит ли анализируемая выборка из генеральной совокупности, имеющей нормальное распределение. Установлено, что р-значения во всех тестах Шапиро превышают критический уровень значимости 0.05 (табл.1), что свидетельствует о соответствии выборок в каждой группе эксперимента нормально распределенным совокупностям.
Таблица 1. Результаты теста на нормальность распределения; приведены величины статистики Шапиро-Уилка W и соответствующие им р-значения
| Уровень флуоресценции | Численность клеток | |||
| Параметры | W | p-value | W | p-value |
| Контроль | 0.8986 | 0.2442 | 0.9228 | 0.5259 |
| Исходная проба | 0.9092 | 0.3102 | 0.8704 | 0.2278 |
| Проба в разведении 1/50 | 0.906 | 0.2887 | 0.9667 | 0.8696 |
| Проба в разведении 1/100 | 0.9 | 0.2518 | 0.9101 | 0.4367 |
Оценку однородности дисперсий (б) проводили с помощью теста Левина (Levene's Test for Homogeneity of Variance). Значение теста Левина для данных по уровню флуоресценции равно 2.5437 при Pr(>F) 0.07358; для данных по численности клеток водорослей – 0.6644 при Pr(>F) 0.5836. Превышение уровня значимости 0.05 в обоих случаях свидетельствует об однородности дисперсий тест-функций для всех условий эксперимента.
Поскольку два формальных условия были выполнены, то был проведен однофакторный дисперсионный анализ ANOVA при помощи базовых функций aov() и lm(). Результаты анализа для данных по численности клеток водорослей выглядят следующим образом (рис. 3).
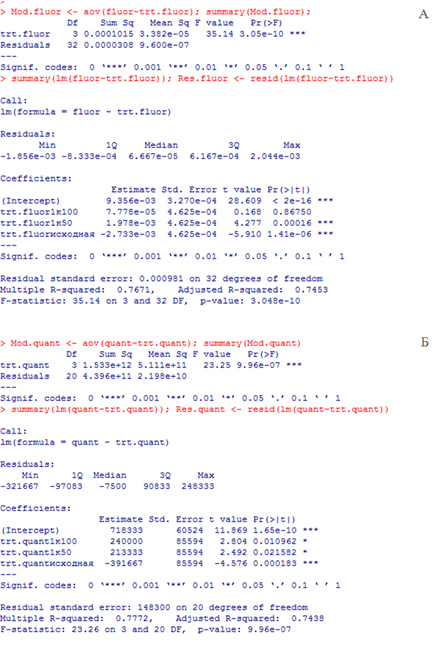
Рис. 3 Результаты однофакторного дисперсионного анализа (ANOVA) данных биотестирования образцов отходов: А) по изменению флуоресценции хлорофилла и Б) прироста численности клеток водорослей
Fig. 3 Results of еру one-way analysis of variance (ANOVA) for the data of biotesting of the waste samples: A) by the change of chlorophyll fluorescence and B) by the increase in the algae cell number
Можно отметить высокие значения коэффициента детерминации R2 = 0.77 и дисперсионного отношения Фишера F = 23.26. что свидетельствует об адекватности построенной модели ANOVA в целом и статистической значимости (р<0.05) предположения о воздействии токсических отходов на изменения численности и флуоресценции водорослей. Анализ коэффициентов линейной модели позволяет проследить эту изменчивость в зависимости от концентрации токсиканта: для контрольных проб средняя численность равна свободному члену модели, т.е. 718333 ед., а в условиях образцов без разведения это значение уменьшается на 391667 ед. Напротив, в условиях больших разведений численность клеток увеличивается по сравнению с контролем на 213333 ед. (1 к 50) и 213333 ед. (1 к 100). Это вполне соответствует современным научным представлениям о возможном увеличении продуктивности популяций в условиях слабого воздействия токсических веществ.
Для данных по уровню флуоресценции хлорофилла F-статистика равна 35.14, а Pr(>F) гораздо меньше критического уровня значимости 0.05. что также свидетельствует о достоверном влиянии концентрации токсичных веществ на изменение этого показателя.
Возвращаясь к исходным предпосылкам дисперсионного анализа (а и б), отметим, что согласно современным представлениям (Grace-Martin, URL) проверка нормальности распределения зависимой переменной Y в группах, выполненная нами в табл. 1, считается необязательной, трудоемкой и недостаточно мощной процедурой. Если рассматривать ANOVA с позиций общей линейной модели, то вместо (а) основным условием корректного анализа является проверка нормальности распределения остатков (т.е. ошибок предсказания). Такая процедура выполняется один раз на всем множестве данных и приводит к однозначному выводу.
Анализ распределения остатков проводили с использованием формальных критериев и графическими методами. Тест Шапиро не отклонил нулевую гипотезу о нормальности распределения ошибок моделей в отношении обеих тест-функций: уровня флуоресценции (W = 0.9767, p = 0.6347) и численности клеток (W = 0.9816. p = 0.924). В качестве графического способа проверки характера распределения использовали построение графика квантилей (quantile-quantile plots). На рис. 4а показаны квантили двух распределений – эмпирического (т.е. построенного по остаткам модели ANOVA) и теоретического (т.е. стандартного нормального распределения). Другим графическим методом является использование функции sm.density() из пакета sm. На графике рис. 4б представлена кривая ядерной плотности для остатков модели и доверительная полоса, построенная методом имитации, что позволяет оценить, насколько правдоподобно предположение о нормальности.
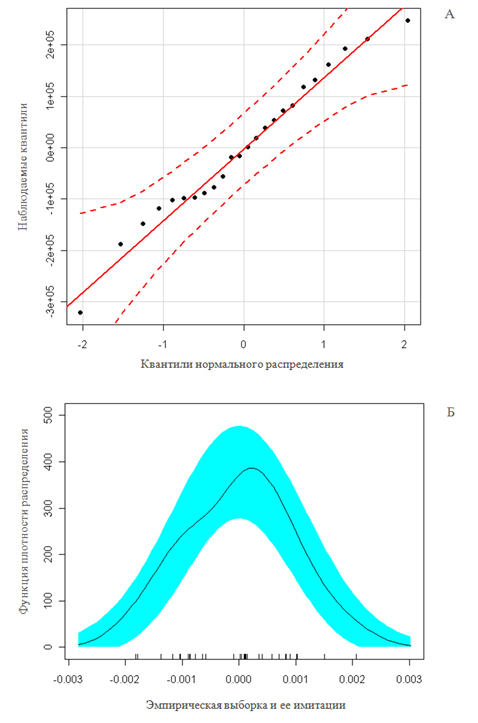
Рис. 4. Анализ характера распределения графическими методами: А) квантильный график ошибок модели для численности клеток, Б) ядерная функция остатков модели для уровня флуоресценции и 95%-ная доверительная полоса, построенная имитационными методами
Fig. 4. Analysis of the distribution by the graphical methods: a) quantile graph of model errors for a cell number, B) nuclear function of model remnants for the fluorescence level and 95% confidence band constructed by simulation methods
Для того чтобы определить, какие именно варианты опыта значимо различаются между собой, выполняли множественные сравнения с использованием алгоритма оценки достоверно значимой разности HSD Тьюки (Tukey multiple comparisons of means - блок 5 в Приложении). Выяснилось, что между контролем и исходной пробой имеются высоко значимые различия как по интенсивности флуоресценции (р = 0.0000081), так и при подсчете численности клеток (p = 0.00097) – см. рис. 5. Столь же значимыми оказались различия между исходной пробой и обоими вариантами с разведением токсических веществ в соотношении 1 к 50 и 1 к 100. Различия между контролем и вариантами с разведением либо отсутствовали, либо проявлялись на уровне значимости, близком к критическому. Можно также отметить, что тест-функция, основанная на подсчете численности клеток, более консервативна к выявлению различий, чем уровень флуоресценции хролофилла.
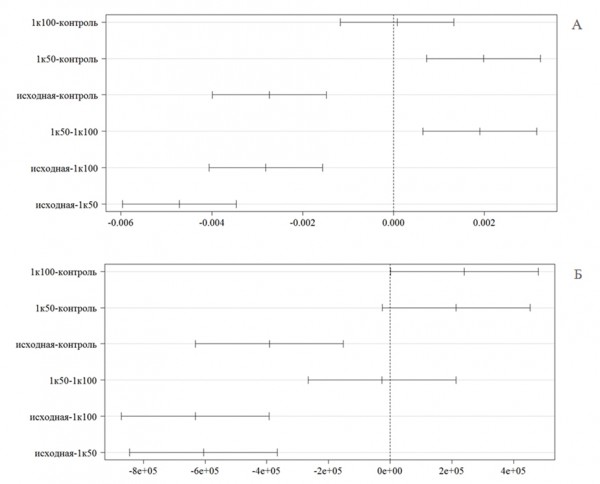
Рис. 5. Графики с 95%-ми доверительными интервалами Тьюки для данных: А) флуоресценции хлорофилла, Б) численности клеток водорослей
(здесь и на рис. 5 по оси абсцисс приведены скорректированные разности средних при парном сравнении различных вариантов эксперимента)
Fig. 5. Graphs for the data (95% confidence intervals for the Tukey test): A) fluorescence of chlorophyll, B) the algae cell number
(here and in Fig. 6 the abscissa axis shows the adjusted difference in mean values while comparing different experiment options in paires)
Существенно более широкие возможности для реализации множественных сравнений предоставляет пакет multcomp, где заложена возможность гибкого управления комбинациями условий межгрупповых сравнений, известных также как простые контрасты. Например, с использованием матрицы контрастов Тьюки можно получить результаты, аналогичные приведенным на рис. 6. Однако часто нам нет необходимости выполнять сравнения для всех возможных парных комбинаций групп с использованием эквивалентных весов, а требуется только осуществить сопоставление контрольного эксперимента с имеющимися вариантами опыта. Для этого нами использовалась матрица контрастов Даннета (Dannet multiple comparisons of means - блок 5 в Приложении). На рис. 5 представлены доверительные интервалы разности средних значений тест-функций между контролем и тремя различными вариантами опыта. Как и в предыдущем случае выявляются статистически значимые различия между контролем и исходной пробой: p = 0.001 при значениях критерия Стьюдента t = -5.910 и t = -4.576 для уровня флуоресценции и численности клеток, соответственно. Здесь важным преимуществом использования пакета multcomp является оценка р-значений рандомизационными методами, что не предъявляет жестких требований к однородности дисперсий. Сравнение контроля с разбавленными образцами показало незначительное превышение значений тест-функций в условиях малых концентраций токсических веществ. Отметим также несколько большую чувствительность теста по интенсивности флуоресценции по сравнению с подсчетом численности клеток.
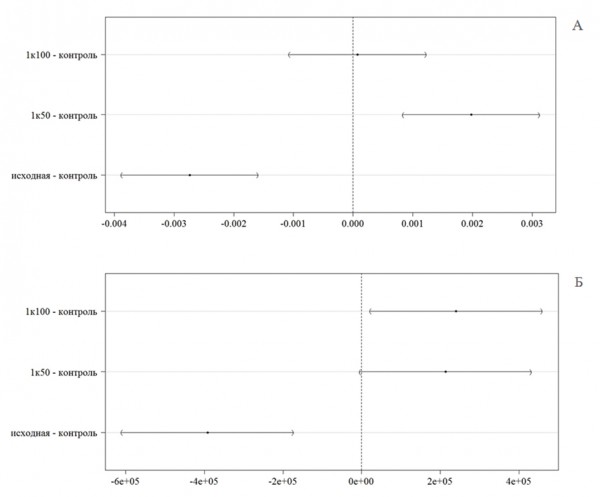
Рис. 6. Графики с 95%-ми доверительными интервалами Даннета для данных: А) флуоресценции хлорофилла, Б) численности клеток водорослей
Fig. 6. Graphs (95% confidence intervals of the Dunnett test) for the data: A) fluorescence of chlorophyll, B) the algal cell number
Представляет методический интерес оценка статистической связи обеих используемых тест-функций. Если между ними наблюдается достаточно тесная зависимость, то это позволит выполнять токсикологический экспресс-анализ, например, по уровню флуоресценции хлорофилла, не прибегая к трудоемкому параллельному подсчету численности клеток водорослей. Для этого по полученным экспериментальным данным рассчитывали коэффициент корреляции Пирсона (Pearson correlation coefficient) и, чтобы не принимать во внимание условие нормальности распределения обеих переменных, дополнительно коэффициент ранговой корреляции Спирмена (Spearman correlation coefficients) (блок 6 в Приложении). Проведенный тест в обоих случаях показал достаточно высокие для биологического эксперимента значения коэффициентов корреляции, которые статистически значимо отличались от нуля: по Пирсону r = 0.715 (p = 0.00915) и несколько ниже по Спирмену r = 0.636 (p = 0.0301).
Для того, чтобы убедиться в линейном характере связи между анализируемыми переменными, построим точечный график линейной зависимости уровня флуоресценции хлорофилла от численности клеток водорослей (рис. 7). Качество аппроксимации линейной моделью хорошо прослеживается в левой части оси абсцисс при численности клеток до 800 тыс. в мл (т. е. в области воздействия токсикантов), тогда как при разведении эта зависимость становится не столь адекватной. Это легко проследить по положению экспериментальных точек относительно 95%-го доверительного интервала. В то же время, если ориентироваться по кривой, сглаживающей конфигурацию точек (smooth curve), закономерной нелинейной зависимости анализируемых переменных не обнаруживается.
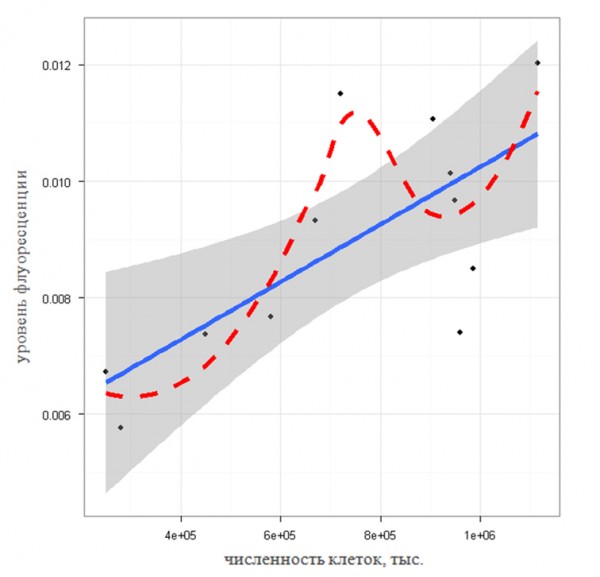
Рис.7. График линейной зависимости уровня флуоресценции хлорофилла от численности клеток водорослей; серым цветом показана 95%-я доверительная область регрессии, красным пунктиром – кривая сглаживания аддитивной моделью GAM
Fig. 7. Graph of linear dependence of the level of chlorophyll fluorescence on algal cell number; the shading shows the 95% confidence region of regression, red dashed line – the curve of smoothing by additive model GAM
Заключение или выводы
Предлагаемые в ряде методик биотестирования способы оценки острой токсичности основаны на частных эвристических предположениях и не могут быть использованы в общем случае для широкого круга тест-функций. Различные тест-функции отличаются друг от друга «статистической эластичностью» и особенностями шкалы измерений, от которых зависит вывод о наличии/отсутствии токсичности. Оценка, действительно ли имеет место токсическое действие, должна основываться на общепринятых принципах проверки статистических гипотез.
Согласно построенной модели однофакторного дисперсионного анализа и проведенных множественных сравнений откликов биотест-системы на основе микроводорослей Ph. tricornutum в результате проведенного нами исследования можно заключить, что имеется статистически значимый эффект воздействия образцов отходов. Эффект обнаруживается по обеим тест-функциям: изменению численности клеток и уровня флуоресценции хлорофилла, - несмотря на то, что во втором случае, согласно методике (Жмур, 2009), исходная проба острой токсичностью не обладает (снижение по сравнению с контролем только на 30%).
Показана статистически значимая корреляция выборочных данных по численности клеток водорослей и уровню флуоресценции хлорофилла. Это позволяет выполнить калибровку их значений и перейти на сокращенный инструментальный анализ результатов биотестирования.
Приведенный в работе скрипт, реализующий все необходимые вычисления в статистической среде R, может быть рекомендован для выполнения расчетов и построения заключений о токсичности анализируемых проб в других биотест-системах.
Библиография
Anderson J.A.H., Hooper M.J., Zak J.C., Cox S.B. Characterization of the structural and functional diversity of indigenous soil microbial communities in smelter-impacted and nonimpacted soils // Environmental Toxicology and Chemistry. V. 28. N 3. 2009. Р. 534–541.
Benjamin I. P. Spatial patterns in benthic biodiversity of Chesapeake bay, USA (1984–1999): association with water quality and sediment toxicity // Environmental Toxicology and Chemistry. V. 21. N 1. 2002. Р. 151–162.
Comparison of statistical packages. URL: http://en.wikipedia.org/wiki/Comparison_of_statistical_packages (дата обращения 16.08.2015)
Free Statistical Software, data and resources. URL: http://freestatistics.altervista.org/?p=stat (дата обращения 16.08.2015)
Frostegåd Å., Tunlid A. and Bååth E. Phospholipid fatty acid composition, biomass, and activity of microbial communities from two soil types experimentally exposed to different heavy metals // Appl. Environ. Microbiol. V. 59. N 11. 1993. P. 3605–3617.
Grace-Martin K. Checking the Normality Assumption for an ANOVA Model. URL: www.theanalysisfactor.com/checking-normality-anova-model (дата обращения 16.08.2015)
R Development Core Team. R: A language and environment for statistical computing. Austria: Vienna, 2013. URL:http://www.R-project.org/ (дата обращения 24.04.2015)
Stefanowicz A.M., Niklin´ska M., Laskowski R. Metals affect soil bacterial and fungal functional diversity differently // Environmental Toxicology and Chemistry. V. 27. N 3. P. 591–598.
Timofeyev M., Shatilina Zh. Different preference reactions of three lake Baikal endemic amphipods to temperature and oxygen are correlated with symbiotic life // Crustaceana. V. 80. N 2. 2007. P. 129–138.
Venables W.N., Smith D.M. An Introduction to R. R Development Core Team, 2014. 105 p. (Рус. пер.: Венэбльз У.Н., Смит Д.М. Введение в R: Заметки по R: среда программирования для анализа данных и графики: пер. с англ. Вер. 3.1.0. Москва, 2014. 109 с.) Yakimenko O., Terekhova V. Humic preparations and the assessment of their biological activity for certification purposes // Eurasian Soil Science. V. 44. N 11. 2011. P. 1222–1230.
ГОСТ Р ИСО 5725-6-2002: Точность (правильность и прецизионность) методов и результатов измерений
Жмур Н.С. Методика определения токсичности водных вытяжек из галитовых отходов и глинисто-солевых шламов, образующихся при производстве калийных удобрений, по снижению темпа роста (снижению численности клеток) и снижению уровня флуоресценции хлорофилла морских водорослей Phaeodactylum tricornutum . М.: АКВАРОС, 2009. 36 с.
Жмур Н.С. Методика определения токсичности воды и водных вытяжек из почв, осадков сточных вод, отходов по смертности и изменению плодовитости цериодафний . М.: АКВАРОС, 2007. 56 с.
Заряднов И.С. Введение в статистический пакет R: типы переменных, структуры данных, чтение и запись информации, графика . М.: Изд-во Российского университета дружбы народов, 2010. 207 с.
Кабаков Р.И. R в действии: Анализ и визуализация данных в программе R / пер. с англ. П.А. Волкова. Москва: ДМК Пресс, 2014. 580 с.
Колеников С.О. Прикладной эконометрический анализ в статистическом пакете Stata : в 2 ч. Москва: РЭШ, 2001. 112 с.
Мастицкий С.Э., Шитиков В.К. Статистический анализ и визуализация данных с помощью R . Москва: ДМК Пресс, 2015. 496 с. URL: http://r-analytics.blogspot.com (дата обращения 16.08.2015)
Трахтенберг И.М., Сова Р.Е., Шефтель В.О., Оникиенко Ф.А. Проблемы нормы в токсикологии . М.: Медицина, 1991. 208 с.
Шипунов А.Б. и др. Наглядная статистика. Используем R! Москва: ДМК Пресс, 2014. 298 с.






 © 2011 - 2026
© 2011 - 2026