Введение
Современная методология оценки техногенной нагрузки и обоснования экологического риска основывается на натурных исследованиях природных экосистем, находящихся в градиенте воздействия. При этом оценка вероятности возникновения отрицательных изменений в окружающей среде (или отдалённых неблагоприятных последствий этих изменений) заключается в выявлении критических точек зависимости доза-эффект, которые интерпретируются «как начало наиболее быстрой трансформации экосистемы, либо как точка, после которой начинается выпадение основных компонентов биоценоза или разрушение системных связей» (Воробейчик и др., 1994).
Важным отличием моделей “доза-эффект” от остальных регрессионных моделей является учет объективной закономерности реакции экосистем на внешнее возмущение, которая имеет, как правило, форму S-образной кривой с наличием резко выраженного перехода между двумя уровнями. При этом в литературных источниках (Finney, 1979; Seber, Wild, 1989; Moore, Caux, 1997; Slob, 2002) представлен обширный набор различных версий таких моделей, которые в частных случаях демонстрируют большую гибкость аппроксимации эмпирических данных и обеспечивают адекватную надежность в области низких уровней эффекта, где неопределенность регрессии традиционно велика, а величина оцениваемого критического значения весьма чувствительна к выбору спецификации модели.
Здесь уместно уточнить терминологию. Под “дозой” мы понимаем любое (химическое, физическое, термическое, биологическое, радиационное) воздействие на экосистему, измеряемое в непрерывной шкале и выражаемое количественно в произвольных единицах измерения. “Эффект” или отклик (англ. response) – реакция экосистемы на воздействие определенного уровня, также выраженная количественно.
При этом различают модели, рассматривающие в качестве эффекта как непрерывные или счетные исходные данные, так и квантованный результат измерений с конечным числом возможных состояний (quantal response). Для непрерывных и счетных данных модель регрессии оценивает натуральную величину эффекта как функцию дозы, тогда как для квантованных данных она предсказывает вероятность того, что при заданной дозе наступит прогнозируемый исход (например, гибель особей). Это различие может быть важным для интерпретации полученных параметров, таких, как пороговая доза, но не является принципиальным обстоятельством при разработке средств моделирования статистической тенденции в эмпирических данных.
Мы в своей публикации преследуем две цели. Одна из них является методической и заключается в рассмотрении некоторых существующих подходов к построению моделей зависимости “доза-эффект”, способам их подгонки и сравнения, а также особенностям интерпретации. Другая цель состоит в рассмотрении применимости этих моделей для оценки экологического риска радиационного загрязнения почвы в ходе карьерной добычи урансодержащих рудных ископаемых.
Материалы
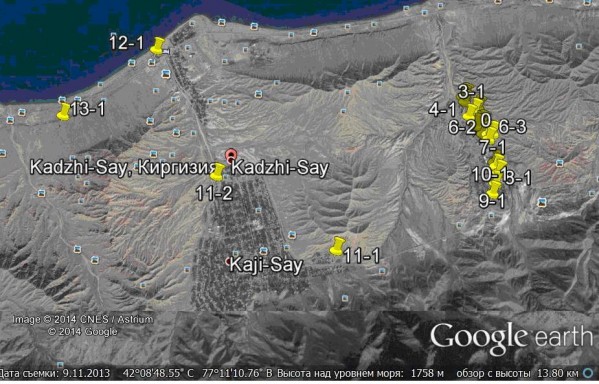
Изучалась территория (рис.1) в районе пос. Каджи-Сай (Кыргызстан), где, начиная с 1947 г., велась разработка урансодержащих месторождений одновременно с добычей лигнита. Содержание урана в породе оказалось крайне низким и в 60-х годах разработку закрывают, но в том же месте стали добывать уголь, которого оказалось довольно много.
Образцы верхних слоев почвы до 25 см отбирались с 22 пробных площадок, находящихся как на территории отвалов урановых шахт, так и в относительно чистых районах (на склонах прилегающего горного массива, по берегу оз. Иссык-Куль и в Боомском ущелье).
Рис 1. Общий план точек отбора проб почвы
Fig. 1. General view of soil sampling points
Почвы исследуемых участков характеризуются как светло-коричневые, типичные для горных долин. Текстура главным образом глинистая, содержащая значительную фракцию каменистых частиц. Содержание гумуса составляет 0.5-1.5 %, общего азота - 0.1-0.2 %, рН имеет отчетливую щелочную реакцию. Растительный покров представлен двумя формированиями: на возвышенностях – травянистый с преобладанием эстрагона (Artemisia dracunculus), а в северной части - доминирующая над травой полынь Федченко (Artemisia fedtschenkoana).
Степень техногенного воздействия на территорию (которая в дальнейшем будет интерпретироваться как “доза”) оценивалась в рамках настоящей публикации по одному из измеренных показателей – объемной активности поверхностного слоя почвы, Бк/кг, за счет распада ядер трех радионуклидов (U-238, Ra-226 и Pb-210). Для измерения активности радионуклидов в отобранных образцах использовался гамма-спектрометр «Canberra» Model GX4019.
Для оценки отклика экосистемы (“эффекта”) использовались данные биологического анализа почвенных образцов, отобранных с изучаемых пробных площадок. Эти биодиагностические данные включали две группы взаимодополняющих показателей: экологические - результаты биоиндикационных исследований сообществ почвенных микроорганизмов и токсикологические – результаты лабораторного фитотестирования (Terekhova, 2011; Terekhova et al., 2014).
Биотестирование с использованием высших растений Sinapis alba проводилось в пластиковых планшетах по показателю средней длины корня проростков семян горчицы белой, выращенных в стандартных условиях на исследуемых образцах почвы (Терехова и др., 2014) .
Биоиндикация сообществ почвенных микроорганизмов проводилась по численности колониеобразующих единиц (КОЕ). Учитывалась общая численность разных структурно-функциональных групп культивируемых микроорганизмов и численность колоний некоторых таксонов (родов) после посева аликвоты водной суспензии из серийного разведения почвенных образцов (1:100) на чашках Петри с питательными средами разного состава (Методы ..., 1991). Инкубация культур осуществлялась в течение 10-14 сут. в термостате при 24 оС (микромицеты) и 28 оС (бактерии и актиномицеты). Статистической обработке подвергали данные из 9 повторностей каждого опытного и контрольного варианта.
Для построения моделей “доза-эффект” использовались показатели численности КОЕ (в 1 грамме воздушно-сухой почвы) микроорганизмов следующих таксономических групп:
- бактерий (млн. КОЕ/г почвы) всего и отдельно по группам, выделенным по отношению к различным формам утилизируемого азота, которые выращивались с использованием трех питательных сред – MPA (мясо-пептонный агар), KAA (крахмало-аммиачный агар) и бульона Чапека;
- актиномицетов (тыс. КОЕ/ г почвы);
- микроскопических грибов (тыс. КОЕ/ г почвы) всего и отдельно по композициям видов родов Penicillium и Aspergillus.
Методы
Статистическая (т.е. основанная на средней тенденции) зависимость φ величины эффекта от уровня воздействия x описывалась моделями, которые в общем виде могут быть представлены как
φ (x; b, c, d, e,...) = с + (d - c) ψ (x; b, e,...),
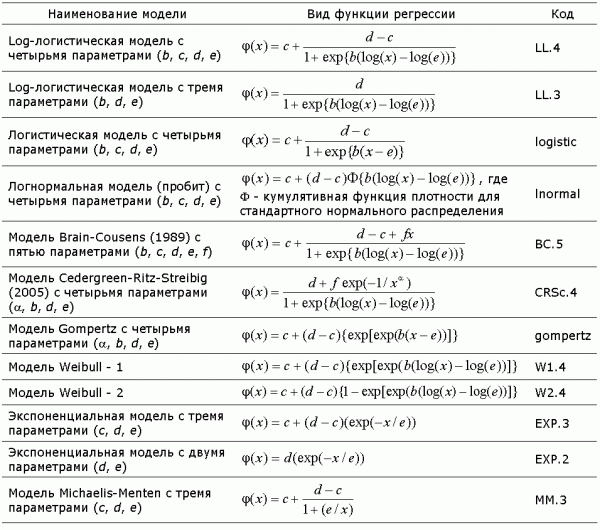
где параметры c и d являются нижним и верхним пределами отклика, а ψ - некоторая задаваемая нелинейная функция с параметрами b и e. Список моделей, протестированных в работе, приведен в табл. 1, в которой использованы наименования и формульная нотация из статьи (Ritz , 2010), претендующей на определенное тематическое обобщение.
Таблица 1. Математические формулы функций нелинейных моделей регрессии, используемых для аппроксимации зависимостей доза-эффект; код соответствует спецификации моделей в пакете drc среды R
Оцениваемые параметры моделей имеют вполне определенный физический смысл. В частности, для лог-логистической модели LL.4 параметры c и d определяют нижнюю и верхнюю горизонтальные асимптоты сигмоидной кривой, e соответствует положению точки перегиба, а d – коэффициенту угла наклона в области переходного состояния. Подгонка (fitting) параметров моделей к анализируемым эмпирическим данным осуществлялась с использованием обобщенного метода минимизации отрицательного логарифма функции правдоподобия. Для отклика, измеренного в непрерывной шкале, минимизировалась сумма квадратов отклонений модельных прогнозов от наблюдаемых значений с учетом специально подбираемых весовых коэффициентов.
Статистический анализ оцениваемых параметров проводился с использованием t-критерия Cтьюдента, с помощью которого проверялась гипотеза о равенстве каждого коэффициента нулю и рассчитывались р-значения, определяющие достигнутый уровень значимости. Проверка статистической значимости модели в целом осуществлялась путем ее сравнения с простой регрессией, имеющей нулевой коэффициент наклона (горизонтальная линия регрессии соответствует отсутствию зависимости доза-эффект). При этом в качестве тестовой статистики для сравнения двух отношений максимального правдоподобия использовался критерий χ2 (Wood, 2006).
Выбор конкретной функции φ из множества представленных в таб. 1 может быть основан на некоторых эмпирических или теоретических предположениях, или, в отсутствии таковых, осуществляться с использованием общепринятых статистических критериев. Нами использовалось стандартное отклонение для остатков Se, а при сравнении двух моделей с разным числом параметров - информационный критерий Акаике AIC, устанавливающий штраф за увеличение размерности модели (Шитиков, Розенберг, 2014).
Важнейшим для биотестирования является построение шкалы изоэффективных доз. Например, если в результате воздействия происходит угнетение жизнедеятельности биологического компонента, то мы можем полагать, что эффективная доза ED10, составляющая 10 % от общего эффекта, представляет собой критический экологический риск. Естественно, если мы анализируем динамику внесения гербицида, то мы должны ориентироваться на дозу внесения ED90, которая вызовет уничтожение 90 % сорняков. Важным опорным параметром является доза ED50, соответствующая 50 %-му сокращению биомассы сорняков или гибели в результате интоксикации половины подопытных животных.
Разность (d - c) параметров модели зависимости отклика от дозы определяет, собственно, величину максимально достижимого эффекта и тогда легко найти любую дозу EDy, которая приводит к (100 - y) % доле от (d - c). Например, для той же модели LL.4 любая изоэффективная доза выражается через параметры b и e :
EDy = e (y / (100 − y))1/b.
Поскольку для всей области определения модели могут быть оценены предикторные доверительные интервалы регрессии, то, тем самым, можно легко обосновать ошибку показателя EDy и другие характеристики его надежности. Заметим, что при использовании исходных данных с откликом, состоящим из квантованных значений 0 и 1, мы имеем (d - c) = (1 – 0) и тогда EDy имеет вероятностный смысл, т.е. дозы, вызывающей регистрируемый эффект у y % особей, взятых в эксперимент.
Расчеты выполнялись с использованием пакета drc статистической среды R (Ritz, Streibig, 2005).
Результаты
В ходе статистической обработки было проанализировано 27 зависимостей девяти различных показателей отклика от трех воздействующих переменных. При этом в каждом случае осуществлялся перебор целого ряда возможных моделей-претендентов из числа представленных в табл. 1. В рамках настоящей статьи мы не имеем возможности привести даже минимальную информацию обо всех построенных моделях, поэтому остановимся далее на некоторых, наиболее характерных из них для каждой группы объектов, используемых в биодиагностике. Поэтому далее акцент будет сделан на использованные методики статистического анализа моделей и особенности их интерпретации.
Актиномицеты. Модели зависимости численности КОЕ культивируемых актиномицетов от активности радионуклида Ra-226 в образцах почвы представлены кривыми характерной сигмоидной формы с четко выраженной областью перегиба (рис. 2).
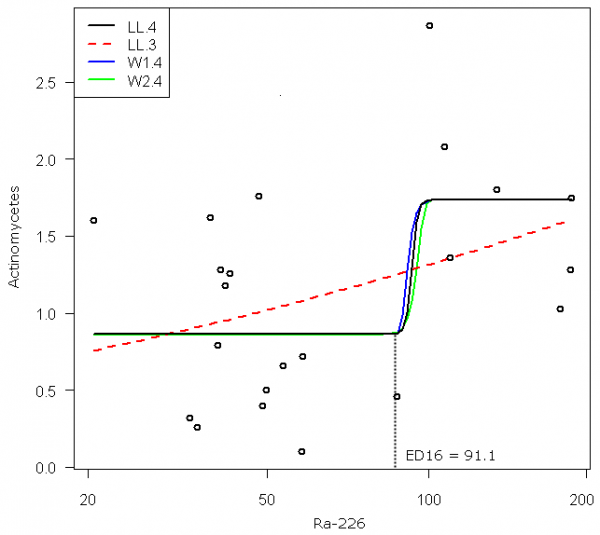
Рис 2. Кривые зависимости численности актиномицетов (тыс. КОЕ/г) от активности радионуклида Ra-226 в образцах почвы (Бк/кг), полученные с использованием четырех различных моделей; здесь и далее ось абсцисс представлена в логарифмическом масштабе
Fig. 2. Dose–response curves for describing the dependences of the number of actinomycete colony-forming units (ths. CFU/g) on the activity of radionuclide Ra-226 in the samples of soil (Bk/kg), using four different models; hereinafter the axis of abscises is presented in the logarithmic scale
Лог-логистическая модель LL.4 является симметричной относительно центральной точки, и ее параметр e численно равен показателю «половинного эффекта» ED50. Статистический анализ значимости оцениваемых параметров по t-критерию приводит к следующим величинам р-значений:
| Параметры | Оценка | Ст.ошибка | t-критерий | р-значение |
| c : Нижний предел | 0.86 | 0.154 | 5.57 | ≈ 0.0 |
| d : Верхний предел | 1.74 | 0.226 | 7.68 | ≈ 0.0 |
| b : Наклон области перегиба | -78.37 | 123.5 | -0.634 | 0.53 |
| e : ED50 | 93.07 | 10.39 | 8.95 | ≈ 0.0 |
Здесь статистически неадекватной является только оценка угла наклона b кривой, что не имеет принципиального значения для обоснования экологического риска. Величина информационного критерия Акаике (AIC = 45.38) для этой модели была минимальной в ряду остальных моделей-претендентов. Набор изоэффективных значений активности Ra-226, оцениваемых по модели LL.4 для последовательности y = {5, 10, 16, 50 и 84%}, представлен в табл. 2.
Модели Вейбулла W1.4 (AIC = 45.41) и W2.4 (AIC = 45.42) с четырьмя параметрами дали в рассматриваемом примере весьма близкие результаты по сравнению с LL.4. Смысл их практического использования в иных случаях связан с асимметрией: кривая Weibull-1 медленнее убывает в области верхнего предела, но быстрее приближается к более низкому пределу, что позволяет точнее отследить зависимость в области низких уровней воздействия (с кривой Weibull-2 имеет место обратный результат).
Имеет смысл задаться важным вопросом: имеет ли какие-либо преимущества нелинейная модель по сравнению с простой линейной моделью? В рассматриваемом случае модель φ(x; d, b) = -0.55 + 0.406 log(х) существенно уступала описанным выше моделям по степени приближения к эмпирическим данным (AIC = 48.45). Уменьшение числа параметров лог-логистической модели до 3 (т.е. нижний предел c = 0) разрушает «сигмоидность» кривой и LL.3 практически сводится к той же линейной зависимости, уступая ей по AIC-критерию (50.28) за счет штрафа за дополнительный параметр.
В последние десятилетия рядом исследований было показано, что при умеренных нагрузках показатели обилия и видового разнообразия некоторых популяций организмов (и почвенных микромицетов, в частности) могут увеличиваться при усилении химического или радиационного воздействия. Поскольку для всех моделей обилие Actinomycetes возрастает при увеличении активности Ra-226 в исследуемых образцах, то очевидно, что в рамках настоящего исследования эта группа почвенных микроорганизмов является достаточно информативным индикатором техногенного загрязнения.
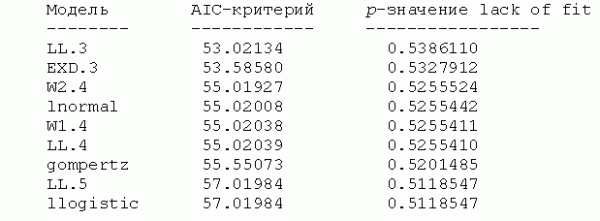
Бактерии. Выполним селекцию моделей для зависимости численности бактерий, утилизирующих минеральные формы азота и выращенных на крахмало-аммиачном агаре (КАА), от активности радионуклида U-238 в образцах почвы:
Представленный список отсортирован по возрастанию AIC-критерия или убыванию математической адекватности, оцениваемой как p-значение для F-критерия в тесте на потерю соответствия (lack of fit - Ritz, Martinussen, 2011). Здесь можно выделить три группы моделей, отличающихся числом параметров (3, 4 и 5) и, в меньшей степени, ошибкой аппроксимации. Однако не всегда разумно руководствоваться при выборе только формальными критериями (тем более, что разность AIC-критериев часто весьма ничтожна) и не принимать во внимание "предметную полезность" модели. В рассматриваемом случае можно отдать предпочтение экспоненциальной модели EXP.3 с тремя параметрами, имеющей лаконичный вид и в явном виде оценивающей величину эффекта (d - c):
φ (x; c, d, e,...) = -8.14 + (2.614 + 8.14)(exp (- x/9971)).
На рис 3 кривая для этой модели сравнивается с моделью LL.4, которая представляет здесь уже не всю сигмоидную кривую целиком, а только ее верхнюю ветвь. Стандартная ошибка экспоненциальной регрессии численно ниже (0.733 против 0.744 для модели LL.4), но если рассчитать отношение Фишера F для средних квадратов остатков, то можно предположить, что отличие качества аппроксимации этими двумя моделями статистически незначимо и, вероятно, обусловлено случайными причинами.
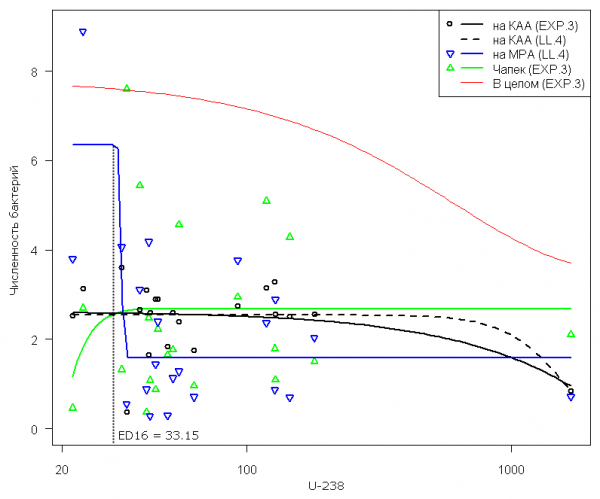
Рис 3. Кривые зависимости численности бактерий (млн. КОЕ/г почвы), выращенных с использованием трех различных питательных сред, от активности радионуклида U-238 в образцах почвы (Бк/кг); здесь и далее в легенде графика в скобках указан тип использованной модели по табл. 1
Fig. 3. Dose–response curves for describing the dependences of the number of bacterial colony-forming units (mln. CFU/g soil) grown using three different nutrient media, on the activity of radionuclide U-238 in the samples of soil (Bk/kg); hereinafter in the legend the type of the used model in the table 1 is indicated n brackets
По аналогичным соображениям можно предпочесть экспоненциальную функцию EXP.3 модели Михаэлиса-Ментен MM.3 для численности сапротрофных бактерий, выращенных на питательной среде Чапека. В отличие от других вариантов выращивания бактерий, их численность в этом случае монотонно возрастает при увеличении радиоактивности U-238. Однако оценки важных параметров обоих экспоненциальных моделей оказались статистически незначимыми (кроме верхнего предела d), поэтому положение аппроксимирующих кривых в области малых значений отклика следует считать достаточно неопределенным.
В противоположность этому, модель LL.4 для численности бактерий, утилизирующих органические формы азота и выращенных на мясо-пептонном агаре (МРА), имеет на графике характерную сигмоидную форму кривой, значимые оценки параметров и обоснованно может использоваться для оценки экологического риска. Набор изоэффективных значений активности U-238, оцененных по этой модели для последовательности y = {5, 10, 16, 50 и 84%}, представлен в табл. 2. Там же для сравнения приведены аналогичные результаты по модели, построенной для суммарной численности бактерий, выращенных на всех трех питательных средах (МРА + КАА + Чапек). Поскольку направленность и скорость развития эффекта для бактерий, выращенных на трех разных средах, различна, то область перегиба совокупной кривой существенно размыта (кривая «В целом» на рис. 3), а ошибка изоэффективных активностей, рассчитанных по суммарной численности, недопустимо велика.
Микроскопические грибы. Анализ зависимости численности (КОЕ/г почвы) культивируемых микроскопических грибов от активности радионуклида U-238 в образцах почвы не привел к построению достаточно работоспособных моделей оценки экологического риска.
Для зависимости численности колоний грибов рода Penicillium выполнять проверку адекватности моделей вообще не требуется, поскольку их тренд практически совпадает со средним значением численности (рис. 4). Например, при построении EXP.2:
φ(x; d, e) = 2.886×exp( - x / 3.2×108) ≈ 2.886.
Также оказалась статистически незначимой модель для суммарной численности микроскопических грибов без разделения на роды Penicillium + Aspergillus + Cladosporium (кривая «В целом» на рис. 4).
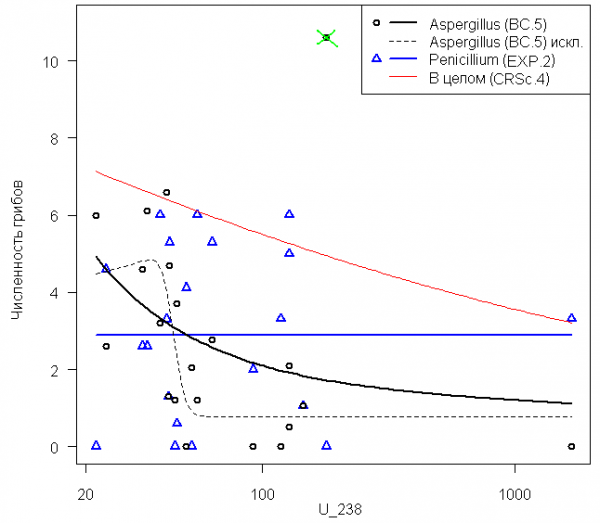
Рис 4. Кривые зависимости численности двух родов микроскопических грибов (тыс. КОЕ/г почвы) от активности радионуклида U-238 в образцах почвы, Бк/кг
Fig. 4. Dose–response curves for describing the dependens of the number of colony-forming units of two genera of microscopic fungi (ths. CFU/g) on the activity of radionuclide U-238 in the samples of soil (Bk/kg)
Тем не менее, обратим внимание на особый смысл использованных здесь моделей Brain-Cousens и Cedergreen-Ritz-Streibig, которые способны учитывать гормезис-эффект (т.е. стимулирующее действие невысоких доз токсикантов; от греч. hórmēsis ). Такие модели могут приводить к кривым с верхним или нижним промежуточным оптимумом. Очевидный пример этому явлению – любые зависимости от воздействия рН, где оптимум обычно располагается в районе рН = 7.
Модель BC.5, построенная для грибов рода Aspergillus, не показывает наличия гормезиса и имеет вид U-образной кривой, плавно стремящейся к 0 при увеличении радиоактивности (рис. 4). Выполним оценку адекватности модели в целом, т.е. проверим требование того, чтобы сумма квадратов отклонений относительно средней численности колоний Aspergillus значимо превышала остаточную сумму квадратов. Этот тест на наличие эффекта дал отрицательный результат: критерий χ2 = 1.47 и р = 0.68. Ошибка и доверительные интервалы такой регрессии оказались слишком велики, что не могло не сказаться на степени достоверности значений изоэффективных доз (см. табл. 2).
Однако легко убедиться, что максимальное значение численности р. Aspergillus, равное 10.6 и отмеченное на рис. 4, может быть квалифицированно как "слишком большое" (outlier). Это подтверждает тест Граббса, который отклонил нулевую гипотезу о том, что это значение не является выбросом: G = 2.85, p = 0.016. Если исключить это аномальное (с точки зрения статистики) наблюдение и вновь построить модель BC.5, то проявляется возможный гормезис-эффект, а функция регрессии становится адекватной в целом: критерий χ2 = 17.6 и р = 0.0015.
Биотестирование с использованием высших растений. Выполним сравнительный анализ моделей LL.4 для аппроксимации зависимости длины корней проростков горчицы белой от активности всех трех радионуклидов (U-238, Ra-226 и Pb-210) – рис. 5. Отметим резкое снижение величины отклика при активности изотопа радия около 30 Бк, что дает возможность принять эту величину в качестве норматива техногенного воздействия – см. табл. 2. Активность иных изотопов также вызывает уменьшение длины корней ростков, однако эта зависимость носит более умеренный и монотонный характер, поэтому локализация их пороговых значений связана со значительной неопределенностью.
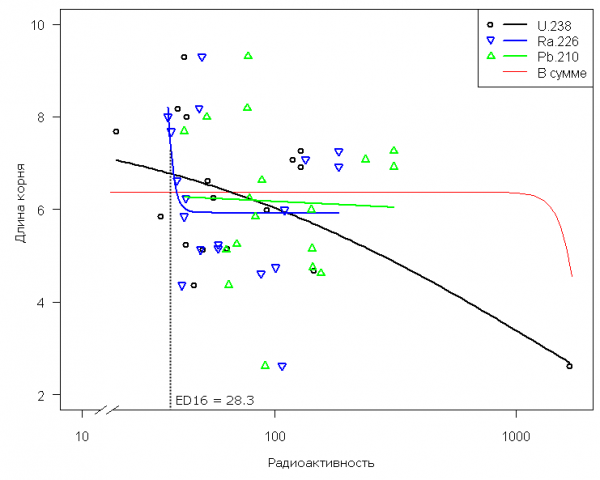
Рис 5. Кривые зависимости средней длины корней проростков горчицы белой (см) от активности трех различных радионуклидов в образцах почвы (Бк/кг) с использованием лог-логистической модели LL.4
Fig. 5. Dose–response curves for describing the dependences of average root length of white mustard (cm) on the activity of three various radionuclides in the samples of soil (Bk/kg) with the use of log-logistical model
Рассмотрим для полноты картины возможность оценки экологического риска с использованием общей радиоактивности почвенных образцов, для чего просуммируем вклады всех трех радионуклидов А = U-238 + Ra-226 + Pb-210. Эта попытка (кривая «В сумме» на рис 5) привела к ожидаемой неудаче, т.к. объединение факторов с различным характером тренда в области малых воздействий приводит к их статистическому нивелированию и последующим некорректным выводам.
Таблица 2. Изоэффективные воздействия радиоактивности нуклидов, полученные в ходе биотестирования для различных уровней проявления эффекта y
| Радионук-лид | Использо-ванный отклик | Эф-фект y % | Оценка воздей-ствия, Бк | Стандартная ошибка | Доверительные границы | |
| нижняя | верхняя | |||||
| U-238 | Уменьшение численности бактерий, выращенных на МРА | 5 | 32.79 | 1.41 | 29.8 | 35.7 |
| 10 | 33.0 | 1.09 | 30.7 | 35.3 | ||
| 16 | 33.15 | 0.87 | 31.3 | 34.9 | ||
| 50 | 33.6 | 0.37 | 32.83 | 34.3 | ||
| 84 | 34.08 | 0.84 | 32.3 | 35.86 | ||
| U-238 | Уменьшение численности бактерий, выращенных на всех средах | 5 | 30.9 | 98.6 | -175 | 237 |
| 10 | 63.5 | 202. | -360 | 487 | ||
| 16 | 105 | 335 | -596 | 806 | ||
| 50 | 417 | 1332 | -2371 | 3207 | ||
| 84 | 1104 | 3523 | -6270 | 8479 | ||
| U-238 | Уменьшение численности грибов рода Aspergillus | 5 | 21.3 | 135 | -262 | 304 |
| 10 | 43.8 | 278 | -538 | 626 | ||
| 16 | 72.6 | 460 | -890 | 1036 | ||
| 50 | 288 | 1829 | -3541 | 4118 | ||
| 84 | 763 | 4838 | -9363 | 10889 | ||
| Ra-226 | Увеличение численности класса Actinomycetes | 5 | 89. | 11.7 | 64.9 | 114 |
| 10 | 90.5 | 11.2 | 66.9 | 114 | ||
| 16 | 91.1 | 10.8 | 68.2 | 114 | ||
| 50 | 93.1 | 10.3 | 71.2 | 115 | ||
| 84 | 95.1 | 10.7 | 72.4 | 117 | ||
| Ra-226 | Уменьшение длины корня проростков горчицы белой Sinapis alba | 5 | 26.5 | 3.4 | 19.21 | 33.79 |
| 10 | 27.5 | 8.7 | 8.84 | 46.16 | ||
| 16 | 28.3 | 13.61 | -0.90 | 57.50 | ||
| 50 | 30.6 | 22.6 | -17.88 | 79.08 | ||
| 84 | 33.2 | 35.9 | -43.82 | 110.22 | ||
Обсуждение
Многие исследователи (Воробейчик и др., 1994; Мотузова, 2000; Shcheglov et al., 2001) отмечают большую пространственную неоднородность техногенного загрязнения почвы. Нередки случаи, когда в центре аномалии есть точки с фоновым содержанием, а на периферии – с содержанием, характерным для центра. Здесь большое влияние оказывают перераспределение концентраций под влиянием осадков в пределах микрорельефа, относительная высота площадок, точечная локализация загрязнений, вариабельность “ассимиляционной емкости” и биологической активности почвы и т.д. Такая неоднородность полей концентрации поллютантов, установленная по результатам анализа проб почвы, заставляет с большой осторожностью относиться к различного рода экстраполяциям точечных наблюдений. В нашем случае разброс эмпирических точек относительно моделируемых кривых также был весьма высок, что не могло не сказаться на статистических критериях значимости оценок.
Поскольку биотические показатели наличия загрязнений обладают большим диапазоном чувствительности к различным поллютантам, то возникает и вторая проблема – поиск “слабого звена” экосистемы и выявление достоверных биоиндикаторов негативного воздействия применительно к конкретным условиям. К сожалению, приходится констатировать, что многие работы биоиндикационного плана, составляющие основу для экологического нормирования, выполняют регистрацию показателей отклика у узкой индикаторной группы, в которой специализируются сами исследователи, вне зависимости от степени ее информативности.
Вряд ли достаточно корректным можно считать вариант свертывания информации с ориентацией на средние показатели или «интегральные индексы», когда объединяются частные факторы и/или отклики на них, имеющие различный (а иногда и противоположный) характер тренда. Например, по результатам настоящей работы, ориентация на суммарные (или относительные средние) численности почвенных микроорганизмов, включая бактерии, актиномицеты и грибы, только усложняет выделение наиболее чувствительных реципиентов среды и является неадекватной целям экологического нормирования.
Использованный нами метод моделирования зависимостей “доза-эффект” для различных комбинаций частных индивидуальных показателей основывается на теоретически глубоко проработанной концепции регрессионного анализа. Оценки параметров моделей и характеристик их адекватности могут быть выполнены с использованием современных статистических методик, таких как бутстреп, байесовские статистики, оценка максимального правдоподобия и т.д. (Шитиков, Розенберг, 2014).
Важнейший результат использования представленных регрессионных моделей заключается в оценке количественных значений переменных x, приводящих к определенной величине эффекта негативного действия (например, значениям концентраций, при которых в ходе биотестирования погибло 5, 16, 50, 86 или 95% тест-организмов). Использование полученной шкалы изоэффективных воздействий позволяет в явном виде обосновать экологический риск ER в виде вероятности (или доле) возможной негативной реакции по наиболее чувствительным биотическим показателям. Как вариант его количественного выражения - отношение шансов, вычисляемое как ER = y(EC) / y(DC) , где y(EC) – доля от максимального эффекта, к которому приводит действующая концентрация токсиканта EC, y(DC) – значение y, принятое при установлении экологической нормы DC (Process…, 2001; Species…, 2002).
Неоднозначным является мнение о том, какую долю от максимального эффекта следует назначать пороговой при обосновании экологического риска. В любом случае, повсеместное использование "магического числа" y = 0.05 многие исследователи считают анахронизмом (хотя бы даже потому, что здесь не ведется проверка нулевой гипотезы). Величина y должна учитывать как статистическую "эластичность" оцениваемых показателей, так и уровень ответственности исследователя за вывод. Принимая во внимание большой размах вариации показателей радиоактивности, мы из экспертных соображений использовали в качестве критического значения ED16 (а также, в некоторой степени, по аналогии с принятой в токсикологии минимальной смертельной дозой ДЛ16, вызывающей гибель 16 % животных).
Результаты моделирования зависимости доза-эффект могут быть использованы для повышения объективности "триадного подхода", все чаще применяемого на практике экологических исследований в качестве комплексной методики обобщения всего массива исследуемых разнородных параметров (Chapman, 2002; Dagnino et al., 2008; Terekhova et al., 2014). При этом формирование локальных индексов биологического, экотоксикологического и химического состояния почвы и выбор весовых коэффициентов для их пересчета в “вероятностную” шкалу будут зависеть уже не от субъективных факторов (например, компетентности экспертов), а основываться на данных статистического анализа.
Заключение
- Проанализирована зависимость динамики биотических параметров (численности почвенных микроорганизмов и ростовых характеристик высших растений) от активности радионуклидов в образцах почвы в зоне разработки урансодержащих месторождений в районе пос. Каджи-Сай (Киргизия). Наиболее информативными индикаторными показателями признаны группы видов актиномицетов и бактерий, утилизирующих органический азот, а также длина корней проростков семян горчицы белой, использовавшейся в качестве тест-культуры.
- Показана эффективность моделирования зависимости отклика от уровня логарифма радиоактивности с использованием логистической регрессии.
- Предлагается принять в качестве экологически допустимой радиоактивности следующие значения воздействия, приводящие к 16% от величины негативного эффекта по наиболее чувствительному биокомпоненту: для активности U-238 – 33.15 Бк/г почвы и Ra-226 - 28.3 Бк/г почвы.
Библиография
Воpобейчик Е.Л., Садыков О.Ф., Фарафонтов М.Г. Экологическое нормирование техногенных загрязнений наземных экосистем (локальный уровень) . Екатеринбург: Наука, 1994. 280 с.
Методы почвенной микробиологии и биохимии . Под.ред. Звягинцева Д.Г. М.: Изд-во Моск. Ун-та, 1991. 303 с.
Мотузова Г.В. Загрязнение почв и сопредельных сред . М.: Изд-во МГУ, 2000. 71 с.
Терехова В.А., Якименко О.С., Воронина Л.П., Кыдралиева К.А. Методика измерений биологической активности гуминовых веществ методом фитотестирования "Фитоскан" . М.: Доброе слово, 2014. 24 с.
Шитиков В.К., Розенберг Г.С. Рандомизация и бутстреп: статистический анализ в биологии и экологии с использованием R . Тольятти: Кассандра, 2014. 314 с. URL: http://www.ievbras.ru/ecostat/Kiril (дата обращения 16.05.2015).
Brain P., Cousens R. An equation to describe dose responses where there is stimulation of growth at low doses // Weed Research. 1989. V. 29. P. 93–96.
Cedergreen N., Ritz C., Streibig J.C. Improved empirical models describing hormesis // Environ. Toxicol. Chem. 2005. V. 24. P. 3166–3172.
Chapman P.A. Decision making framework for sediment assessment developed for theGreat Lakes// Human and Ecological Risk Assessment. 2002. V. 8. № 7. P. 1641–1655.
Dagnino A., Sforzini S., Dondero F. et al. "Weight-of-Evidence" approach for the integration of environmental ‘‘Triad’’ data to assess ecological risk and biological vulnerability // Integr. Environ. Assess. Manage. 2008. № 4. Р. 314–326
Finney D.J. Bioassay and the Practise of Statistical Inference // Int. Statist. Rev. 1979. V. 47. P. 1–12.
Moore D.R., Caux P.Y. Estimating low toxic effects // Environ. Toxicol. Chem. 1997. V. 16. P. 794-801.
Process for Conducting Probabilistic Risk Assessment // Risk Assessment Guidance for Superfund (RAGS). 2001. Vol. III. Part A. 385 p.
Ritz C. Towards a unified approach to dose-response modeling in ecotoxicology // Environ. Toxicol. Chem. 2010. V. 29. P. 220–229.
Ritz C., Martinussen T. Lack-of-fit tests for assessing mean structures for continuous dose-response data // Environmental and Ecological Statistics, 2011. V. 18. P. 349–366.
Ritz C., Streibig J.C. Bioassay analysis using R // J. Stat. Soft. 2005. V. 12. P. 1-22.
Seber G.A., Wild C.J. Nonlinear Regression.New York: John Wiley, 1989. 768 р.
Shcheglov F.I., Tsvetnova O.B., Klyashtorin A.L. Biogeochemical migration of technogenic radionuclides in forest ecosystems. M.: Nauka, 2001. 235 p.
Slob W. Dose-response modeling of continuous endpoints // Toxicol Sci. 2002. V. 66. P. 298–312.
Species sensitivity distributions in ecotoxicology / Ed. by Posthuma L., Suter G., Traas T. Boca Raton: Lewis Publishers, 2002. 587 p.
Terekhova V.A. Soil Bioassay: Problems and Approaches //Eurasian Soil Science. 2011. V.44, no 2. P. 173–179.
Terekhova V., Pukalchik M., Yakovlev A. The triad approach to ecological assessment of urban soils // Eurasian Soil Science. 2014. V. 47, no. 9. P. 952–958.
Wood S.N. Generalized Additive Models: An Introduction with R. Chapman, Hall/CRC, 2006. 410 p.
Благодарности
Работа поддержана грантом МНТЦ (KR-2092).






 © 2011 - 2026
© 2011 - 2026