Введение
Одним из эффективных методов выявления механизмов функционирования популяции в ходе ее адаптации к новым условиям обитания является моделирование процессов пополнения, роста и убыли (Drury et al., 2007). Закономерности формирования популяционной структуры вида могут быть выражены количественно через параметры взаимодействия этих популяционных процессов. Несмотря на интенсивную двадцатилетнюю историю исследований камчатского краба Баренцева моря, многие аспекты оценки его популяционных параметров, в том числе и важные для промысла, остаются малоизученными. Моделирование индивидуального и группового роста ракообразных, в отличие, например, от рыб, сопряжено с трудностью определения точного возраста. Камчатский краб растет в течение короткого периода после линьки, т. е. индивидуальный рост особей имеет сложный прерывистый характер. Частота линьки зависит от пола, возраста и условий обитания краба. Традиционные модели с использованием численности поколений становятся трудноприменимыми (Smith, Addison, 2003). Кроме того, камчатский краб для Баренцева моря – инвазийный вид, интродукция которого была осуществлена в 60-е годы прошлого столетия. При взрывном характере численности, который часто наблюдается у акклиматизированных животных, моделирование динамики численности и оценка экологической емкости среды для интродуцента имеет существенные неопределенности и затрудняет принятие допущения о динамическом равновесии популяции, необходимом в традиционном моделировании системы «окружающая среда – запас – промысел». В период открытия коммерческого промысла камчатского краба (2004–2007 гг.) одной из главных проблем в определении продуктивности баренцевоморской популяции камчатского краба являлся его незаконный промысел, который не поддавался точной оценке. По экспертным оценкам российских исследователей, незаконный экспорт, нелегальный вылов и браконьерство, наряду с несовершенной системой контроля промысла, не позволяли оценить реальные объемы добычи краба и, соответственно, затрудняли определение уровня эксплуатации и продуктивности популяции. В процессе разработки модельных подходов к динамике численности камчатского краба в Баренцевом море был выработан алгоритм аналитической оценки, который учитывает все вышеизложенные аспекты, однако сами подходы по сей день подвергаются изменениям. Причины таких изменений связаны, прежде всего, не со стремлением усовершенствовать математический аппарат процедуры, а с необходимостью учитывать меняющееся качество и объем исходных данных, получаемых в ходе ежегодных исследований. Сокращение объемов финансирования исследований и, как следствие, изменения в методике проведения исследовательских съемок стали причиной пересмотра существующих процедур оценок в последние годы. В условиях плохой информационной обеспеченности исследований величины параметров зачастую находят, используя алгоритмы на основе формулы Байеса, когда в качестве исходной информации берутся не только данные наблюдений, но и априорное (предварительное) знание о параметрах модели (Bayes, 1763). История применения подходов на основе теоремы Байеса в популяционной биологии насчитывает порядка 20 лет (Burgner, 1991; Angel et al., 1994; Schnute, 1994; Punt, Butterworth, 1996; Kinas, 1996; Meyer, Millar, 1999; Patterson, 1999). В настоящее время такие подходы широко используются для описания состояния и прогнозирования динамики запасов морских млекопитающих, рыб и беспозвоночных. Модели, использующие теорему Байеса, были успешно адаптированы для оценки запасов северной креветки, синего краба, канадского лосося, южноафриканского анчоуса, усатых китов, тихоокеанских тунцов, палтуса и сельди (Butterworth, Punt, 1995; Schnute et al., 1998; Meyer, Millar, 1999; Millar, Meyer, 2000). Оценки состояния запасов и прогнозы, выполненные при помощи таких моделей, используются в различных международных организациях, участвующих в формировании рекомендаций по эксплуатации гидробионтов: ФАО, АНТКОМ, НАФО, ИКЕС, НЕАФК (Annala, 1993; Adkison and Peterman, 1996; McAllister and Kirkwood, 1998; Punt, Hilborn, 2001; Hvingel and Kingsley, 2006; ICES, 2008). В настоящей работе описан опыт моделирования динамики популяции камчатского краба в Баренцевом море на основе байесовского подхода. Дается краткий обзор методов когортного и продукционного анализа популяционных параметров с учетом экологических особенностей этого ракообразного и методов сбора информации. Рассматривается методика применения байесовского подхода на примере оценки параметров продукционной модели.
Аналитический обзор
Модели популяционной динамики
Для оценки биологических показателей популяции камчатского краба в Баренцевом море в 2003 г. была осуществлена первая попытка моделирования динамики его численности. Модель описывала элементарные биологические процессы и базировалась на традиционных биостатистических методах, разработанных для оценки эксплуатируемых популяций рыб. Рассматривая динамику численности одного поколения, профессор Ф. И. Баранов вывел в 1918 г. соотношение, на которое опирается в настоящее время большинство биостатистических моделей (Баранов, 1918):
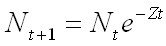 , [1]
, [1]
где Nt – численность поколения в начальный момент времени t, Nt+1 – численность в момент времени t + 1, e – основание натуральных логарифмов. Показатель степени Z называется коэффициентом мгновенной общей смертности (Рикер, 1979; Шибаев, 2007). Смысл коэффициента: за элементарный (очень маленький) промежуток времени dt численность животных уменьшается на величину dN, равную Z-й части от фактической численности N или dN / dt = –ZN. Для эксплуатируемых популяций гидробионтов Z определяется изъятием животных промыслом (коэффициентом мгновенной промысловой смертности, F) и всеми остальными причинами, кроме промысла (то есть коэффициентом мгновенной естественной смертности, M) : Z = F + M.
Спустя 40 лет J. A. Gulland (1964) и G. I. Murphy (1965) предложили метод анализа структуры уловов эксплуатируемых популяций рыб на основе подхода Ф. И. Баранова. Использовались два уравнения. Первое отражает взаимосвязь численностей смежных возрастных групп:
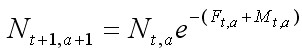 , [2]
, [2]
Второе уравнение позволяет рассчитать величину улова в поштучном выражении, получаемого от каждой возрастной группы:
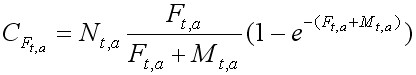 , [3]
, [3]
где Nt, a , Nt+1, a+1 – начальная численность возрастной группы a в году t и в следующем t + 1 году, когда возраст рыбы увеличится на единицу; CF – улов возрастной группы a в году t; Ft,a, Mt,a – коэффициенты мгновенной промысловой и естественной смертности возрастной группы a в году t. Они могут быть зависимыми или независимыми от возраста, а величина F может изменяться по годам в связи с изменениями интенсивности промысла. Уравнения служат базовыми для группы методов, широко используемых в настоящее время в промысловой ихтиологии, которая называется виртуально-популяционным анализом ( Murphy, 1965; Pope, 1972; Jones, 1974; Рикер, 1979).
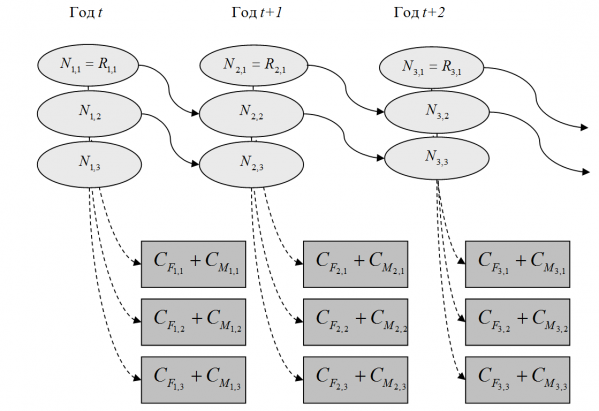
При виртуально-популяционном анализе, как правило, начальная численность Nt,1 определяется величиной пополнения Rt,1, то есть количеством особей, пополнивших в году t промысловый запас (Рикер, 1979). Обозначим количество животных, погибших по естественным причинам, символом Ct,a, тогда схему эксплуатируемой популяции рыб, согласно уравнениям [2] и [3], можно представить графически (рис. 1).
Рис. 1. Блок-схема моделирования динамики численности эксплуатируемой популяции (сплошные стрелки – переход выживших особей в следующую возрастную группу, пунктирные стрелки – убыль животных от промысловой и естественной смертности)
Fig.1. Block diagram of modeling the dynamics of the size of an exploited population (solid arrows – the transition of survivors into the next age group, the dashed arrows – the loss of animals from fishing and natural mortality)
Виртуально-популяционный анализ динамики численности промысловых ракообразных на основе возрастных когорт не получил широкого применения в силу сложности определения точного возраста животного (ICES, 2001a; ICES, 2001б). Однако с начала 90-х годов прошлого столетия, основные принципы изменения численности поколений, разработанные Ф. И. Барановым, стали с успехом применяться в моделировании динамики численности крабов и креветок (Collie, 1991; Kruse and Collie, 1991; Zheng et al., 1995; Quinn et al., 1998; Cadrin, 2000). Модели этого типа базировались на изменениях численности не поколений, а размерных групп (LBA, length-based analysis) и учитывали линьку и стохастический рост животных.
Для популяции камчатского краба Баренцева моря модель LBA была реализована в 2003 году и стала использоваться с 2006 года, когда временной ряд наблюдений составил 13 лет (Баканев, 2006). Рассмотрим принцип моделирования динамики численности эксплуатируемой популяции камчатского краба на основе модели LBA, описанной в работе J. Zheng и др. (1995). Численность краба моделировалась раздельно по размерным группам l = 1, 2, 3, … i и по полу. Каждая размерная группа l в году t состояла из особей с новым (Nl,t) и старым (Ol,t) карапаксом. В течение года t крабы как с новым, так и старым панцирем могут линять с вероятностью ml,t или с вероятностью 1 – ml,t, не линяя, оставаться в этой же размерной группе.
Вероятность линьки для краба ml,t была представлена логистической функцией (Balsiger, 1974):
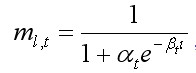 , [4]
, [4]
где at и bt – параметры, l – средняя длина размерной группы l.
Нелиняющие крабы Nl,t и Ol,t в году t + 1 становились Ol,t+1 в таком соотношении:
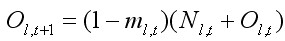 , [5]
, [5]
Линяющие крабы в t году – ml,t( Nl,t + Ol,t), в году t +1 в зависимости от длины прироста попадают в последующие размерные группы и становятся крабами с новым карапаксом, принадлежащими размерным группам 1, 2, 3, …, L. Вероятность перехода в определенную группу зависит от параметров прироста краба за одну линьку. Рост на индивидуальном уровне характеризуется длиной прироста особи. Длина прироста особи на групповом уровне варьирует как внутри размерной группы, так и между группами. Средний прирост особи камчатского краба для размерной группы l (Gl,) обычно выражали линейной функцией от средней длины (l) размерной группы l перед линькой краба (Weber, Miahara, 1962):
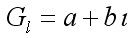 , [6]
, [6]
где a и b – параметры линейной функции.
Отклонения прироста особей размерной группы l за линьку от уравнения регрессии описывали через вероятностное распределение. Плотность вероятности величины прироста выражали через гамма-распределение, форма которого, в зависимости от значений параметров, охватывает все возможное многообразие изменений в распределении прироста (Sullivan et al., 1990):
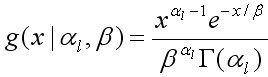 , [7]
, [7]
где x – величина прироста во время линьки, al и b – параметры. Средняя x задавалась произведением al · b и равна G. Так al = G / b, тогда прирост выражался посредством двух параметров G и b. Ожидаемая пропорция крабов размерной группы l, переходящих после линьки в последующую группу l', равна интегралу функции гамма-распределения на интервале группы l':
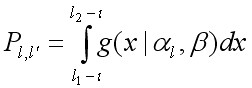 , [8]
, [8]
где l – средняя длина группы l, l1 – начало интервала группы l', l2 – конец интервала группы l'. Для последней размерной группы L, PLL = 1.
Пополнение (R) моделируемой популяции камчатского краба американские исследователи описали с помощью двух параметров: 1) количество молодых крабов, пополняющих популяцию в году t, Rt и 2) параметр Ul, определяющий стохастическое изменение процесса пополнения (Sullivan et al., 1990; Zheng et al., 1995). Пополнение каждой размерной группы Rl,t выражалось через уравнение:
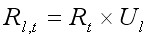 , [9]
, [9]
где Ul описывалось гамма-распределением, таким же как в уравнениях [7] и [8] с параметрами ar и br и. Средний размер пополнения задавался произведением ar · br, поэтому требовалось оценить только параметр br, при условии, что был известен средний размер пополнения.
Учитывая описанные выше вероятностные процессы в динамике численности камчатского краба, моделируемую популяцию удобно представить в каждый момент времени вектором, состоящим из численности размерных групп:
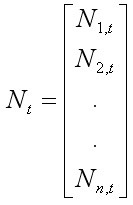 , [10]
, [10]
где Nt – вектор L размерных групп, показывающий общее количество животных с новым карапаксом в году t. Расчет Nt+1 обеспечивает матрица переходов (transition matrix), содержащая параметры стохастического роста (m, P) и пополнения (R):
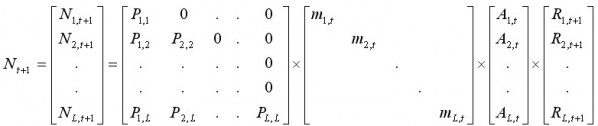 , [11]
, [11]
где Al,t – временная переменная, показывающая остаточную численность краба с новым и старым карапаксом в размерной группе l с учетом вылова, и равная:
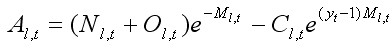 , [12]
, [12]
где Nl,t и Ol,t – численности крабов с новым и старым карапаксом в размерной группе l в году t соответственно; Cl,t – вылов крабов (экз.) размерной группы l в году t; Ml,t – коэффициент мгновенной естественной смертности для крабов размерной группы l в году t и yt – временнáя задержка от момента съемки до средней даты периода промысла. Расчет переменной Al,t основывается на подходе Ф. И. Баранова, описанном уравнениями [2] и [3]. Он также схематично представлен на рисунке 1.
Основная сложность реализации методов, основанных на когортном анализе, заключается в том, что для исходных систем уравнений трудно получить однозначное решение, особенно в случае низкого качества входных данных (Бабаян, 2000). Так, для баренцевоморской популяции камчатского краба короткий ряд наблюдений, относительно низкие уловы крабов в ходе ежегодных съемок, недооценки численности вследствие активных миграций акклиматизанта, неопределенности в оценке общего вылова, а также методические ошибки в ходе становления нового ряда наблюдений вносили существенные помехи в оценку параметров запаса и затрудняли выявление закономерностей его динамики.
Характер изменений в численности, значительные выбросы в оценках и тренды в остатках свидетельствовали о низкой надежности полученных оценок по модели LBA. Большое количество параметров делали модель излишне сложной, что не могло быть оправдано качеством входных данных, допущений и теорий, которые поддерживали такие допущения.
В настоящее время расчеты не показали хороших перспектив для использования стохастической версии модели LBA как инструмента оценки динамики запаса и ориентиров управления для баренцевоморского запаса камчатского краба. Учитывая негативные тенденции в ежегодных исследованиях и сокращении объемов ежегодно собираемой информации, в настоящее время стало целесообразно использовать более простые модели, основанных на меньшем количестве когорт.
На основе модели LBA в 90-е годы прошлого столетия был разработан целый ряд моделей, успешно использующих возможности анализа размерных рядов (Collie, 1991; Kruse and Collie, 1991; Zheng et al., 1995; Quinn et al., 1998; Cadrin, 2000). Одна из них, CSA (catch survey analysis), является частным случаем LBA, когда численность популяции мала для получения качественных данных по размерному составу. Модель была разработана Зенгом и др. (Zheng et al., 1997) для небольших запасов краба с относительно низкими уловами в ходе ежегодных съемок. Обе модели принципиально сходны. Отличие состоит лишь в том, что в модели CSA используются более укрупненные размерные группы, а в расчетах приемлемо использовать данные по размерному составу лишь половозрелых самцов. В модели CSA деление на размерные группы, как правило, основывается на особенностях биологии и промысла дальневосточных крабов семейства Lithodidae, в которое входит и камчатский краб. Промысловая часть популяции в году t, состоящая из крупных самцов, делится на две группы: рекруты (REt) и пострекруты (POt). REt – это численность крабов с новым карапаксом, пополнивших промысловый запас в году t. Рекруты принадлежат размерной группе, начало которой равно минимальному промысловому размеру, а длина интервала размерной группы соответствует средней длине прироста рекрута за одну линьку. POt– численность крабов, пополнивших промысловый запас в году t – 1 и ранее. Пострекруты это все промысловые крабы со старым карапаксом, а также особи с новым панцирем, имеющие размеры большие, чем рекруты. Пополнением промыслового запаса считаются пререкруты (PRt) – особи, которые в следующем году станут рекрутами. Пререкруты принадлежат размерной группе, конец интервала которой граничит с минимальным промысловым размером, а длина интервала соответствует средней длине прироста пререкрута за одну линьку. Динамику моделируемой популяции можно представить в виде уравнений:
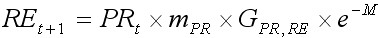 , [13]
, [13]
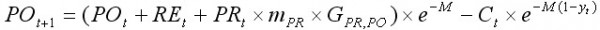 , [14]
, [14]
где mPR – вероятность линьки для пререкрутов; GPR,RE, GPR,RO – параметры роста, соответствующие доле крабов, которые переходят из группы PRt в группу REt+1 и из группы PRt в группу POt+1; M – коэффициент естественной смертности; Ct – вылов крабов в году t; yt – временнáя задержка от момента съемки до средней даты периода промысла.
Адаптация опыта американских ученых и результаты наших исследований показали хорошие перспективы для использования стохастической версии модели CSA как инструмента для оценки динамики запаса, отслеживания реакции популяции на промысел, оценки ОДУ и ориентиров управления для баренцевоморского запаса камчатского краба (Баканев, 2003, 2008). Результаты оценок популяционной динамики камчатского краба в Баренцевом море по модели CSA показали лучшую согласованность исходных индексов численности и модельных значений по сравнению с результатами использования модели LBA. Кроме того, относительная простота и меньшее количество параметров модели CSA делают ее менее чувствительной к качеству исходной информации.
Описанные ранее модели LBA и CSA, основанные на динамике численности размерно-возрастных групп, требуют как минимум наличия исходных данных о размерно-возрастной структуре популяции на протяжении достаточно продолжительного временного ряда. Такая исходная информация об эксплуатируемой популяции, как правило, собирается в результате ежегодного мониторинга промысла и выполнения научно-исследовательских съемок. Нарушение методик выполнения съемок в последние годы привело к поиску альтернативных методов оценок динамики численности популяции камчатского краба. При дефиците биологической и промысловой информации моделируемая численность может быть выражена упрощенно через изменение производительности промысла и величине вылова (Бабаян, 2000; Баканев, 2009).
В практике управления запасами водных биологических ресурсов широко применяются продукционные модели и так называемые модели истощения, основанные на изменении производительности промысла как показателя состояния всей популяции или ее части, на которой ведется промысел (Haddon, 2001).
Для баренцевоморской популяции камчатского краба продукционная модель была адаптирована в 2006 году с открытием полномасштабного коммерческого промысла краба. Дискретная форма записи модели при отсутствии промысла имеет вид (Schaefer, 1957):
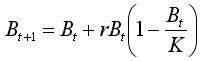 , [15]
, [15]
где Bt – биомасса животных в году t, K – максимальная возможная биомасса при отсутствии промысла (емкость среды), r – коэффициент мгновенного популяционного роста (внутренняя скорость роста) в отсутствие плотностной регуляции. Согласно свойству этого логистического уравнения максимальные продукционные способности запаса наблюдаются при биомассе, равной K / 2.
Однако продукционный подход к динамике искусственно созданной популяции показал весьма ненадежные результаты. Для растущей популяции, постоянно увеличивающей свой ареал, определение емкости среды связано с большой степенью риска получить искаженную истинную картину. Очевидно, что роль оценки запаса не заключается в угадывании наилучшего значения K. В большей степени она должна обеспечивать помощь системе управления промыслом, чтобы можно было реагировать на различные типы природных флуктуаций. Роль оценки запасов состоит не в определении статичных величин оптимальных промысловых усилий и уравновешенных выловов, а в оценке реакций промысловых популяций и рыбаков на управляющие решения и другие воздействия.
Тем не менее, несмотря на высокую неопределенность, стохастический вариант модели обеспечивает в настоящее время аналитическую альтернативу существующим методам оценки численности камчатского краба. Комплексный подход учитывает ошибки наблюдений и позволяет связывать уравнение динамики популяции с наблюдаемыми промысловыми показателями. Вероятностные оценки также позволяют рассчитывать риск превышения того или иного ориентира управления, что делает модель привлекательной для использования в принятии управленческих решений. При продолжении ряда наблюдений, устранении неопределенности в оценке ежегодного вылова и полной натурализации интродуцированного запаса степень надежности оценки параметров продукционной модели должна значительно возрасти.
Другой альтернативой размерно-возрастным моделям в настоящее время становится модель истощения Лесли (Leslie depletion model; Haddon, 2001). Модель основана на динамике снижения производительности промысла в течение промыслового сезона и используется для оценки численности на начало промыслового сезона с учетом темпов снижения.
Учитывая относительно короткий период промысла (2–3 месяца), делается допущение, что величина естественной смертности за период промысла незначительна, и ей можно пренебречь. Тогда уравнение динамики численности на акватории промысла будет выглядеть так: Nt+1 = Nt + Ct. Численность на начало промыслового сезона (Nt+1) при этом будет равна сумме численности на конец сезона (Nt) и кумулятивному вылову (Ct) между временем 1 и t. При этом N может быть выражен через улов на усилие или производительность (U) и коэффициент улавливаемости: U = qN, где U – улов на усилие, q – коэффициент улавливаемости. С учетом коэффициента улавливаемости, уравнение динамики численности на акватории промысла будет выглядеть так: Ut+1 = Ut + qCt. Уравнение имеет вид линейной регрессии, с помощью которого может быть вычислен q и, соответственно, N. Для оценки численности камчатского краба в начале промыслового сезона в Баренцевом море используются данные промысловой статистики 2007–2012 гг., с учетом того, что в этот период промысел был локализирован в одних и тех же районах, а степень неучтенного вылова значительно снизилась. Характер снижения производительности с учетом возрастающего вылова к концу промыслового сезона используется для расчета численности запаса на акватории промысла в период этого промыслового сезона.
Методы оценки параметров
Процесс оценки параметров эксплуатируемой популяции можно представить в виде двух взаимосвязанных основных этапов:
1) построение модели исследуемого явления;
2) оценка основных характеристик (параметров) модели по данным наблюдения.
Основы первого этапа, описанные в предыдущей главе, заложены к середине прошлого века и не претерпели существенных изменений (Рикер, 1979, Одум, 1986). Второй этап опирается на методы математической статистики, которые в настоящее время продолжают активно развиваться (Punt and Hilborn, 1997; Schnute et al., 1998).
Стохастическая природа оцениваемых параметров может быть описана с использованием различных алгоритмов идентификации, наиболее распространенным из которых является метод максимального правдоподобия (Hilborn and Walters, 1992). Точность получаемых оценок параметров зависит от полноты и качества исходной информации. Фрагментарность данных, ошибки измерений, шум природных процессов в совокупности с короткими рядами наблюдений могут значительно исказить результаты оценок и, соответственно, понимание реальных биологических явлений (Васильев, 2001).
В условиях плохой информационной обеспеченности оценки параметров зачастую находят, используя алгоритмы на основе формулы Байеса, когда в качестве исходной информации берутся не только данные наблюдений, но и априорное (предварительное) знание о параметрах модели (Bayes, 1763). Подход основан на попытке начать статистический вывод с некоторых исходных предположений (догадок) о вероятностном распределении неизвестных параметров. Значения модельных параметров можно установить априорно на основе оценок, полученных, например, для одних и тех же видов, но из разных районов, или для схожих видов из одного района. Используя теорему Байеса, окончательные (апостериорные) значения параметров оцениваются с учетом как данных наблюдений, так и предварительно заданных значений параметров:
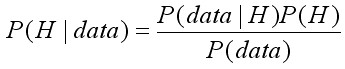 , [16]
, [16]
Здесь распределение P(H) называется априорным распределением вероятностей возможных значений параметра или параметров H (это распределение принимается прежде, чем получены статистические данные); data – статистические данные, полученные в ходе эксперимента (наблюдений, опытов), которые используются в модели; P(H | data) – условная апостериорная вероятность, количественно оценивает насколько модель соответствует гипотезе H в условиях, характеризуемых данными наблюдений (data); P(data | H) – функция правдоподобия, используемая в традиционном статистическом оценивании параметров, которая определяет вероятность того, что полученные данные в ходе эксперимента соответствуют гипотезе H .
В рамках байесовского подхода, гипотезы (параметры) трактуются как случайные величины и описываются с использованием вектора непрерывных значений параметров вместо набора дискретных значений. Вероятности в этом случае будут выражаться через плотности вероятностей, а знаменатель P(data) в уравнении [16] согласно формуле полной вероятности будет равен
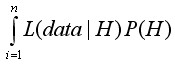 .
.
Функцию Байеса можно представить иначе, в виде трех составляющих:
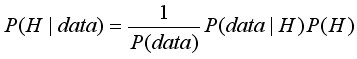 , [17]
, [17]
где 1/P(data) некая постоянная величина по отношению к гипотезе. Поэтому апостериорное распределение пропорционально произведению функции правдоподобия на априорное распределение или:
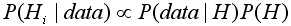 , [18]
, [18]
где символ µ означает пропорциональность.
В терминах статистики байесовский подход базируется на следующих четырех компонентах. Априорная (предварительная) информация (PRIORS) и данные (DATA), полученные в ходе эксперимента, объединяются с помощью некоего метода (method) для получения апостериорного (POSTERIORS) знания. Эти компоненты могут быть представлены в виде:
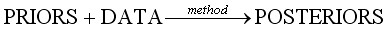 , [19]
, [19]
Входной компонент DATA представляет собой индексы численности краба, оцененные по съемкам, и вылов. В качестве компоненты PRIORS берется предварительное (приблизительное) знание о параметрах модели, количественно представленное в виде распределений вероятностей их возможных значений. В качестве компоненты POSTERIORS выступает существенно уточненное знание о параметрах модели, также представленное в виде распределений вероятностей значений. Метод расчета POSTERIORS зависит от сложности моделируемых процессов. Для описания биологических процессов с высокой степенью неопределенности использовался алгоритм вычисления, основанный на построении цепи Маркова (рис. 2). Для этого применяется итерационная процедура, на каждом шаге которой рассчитываются модельные значения параметров и переменных. Каждый итерационный шаг включает в себя три этапа.
На первом этапе первой итерации происходит расчет численности животных (data) по биологической модели (BIO) с использованием стартовых (начальных) значений параметров и переменных (INITS). Биологическая модель в нашем случае представляет собой одну из четырех, описанных ранее: LBA, CSA, продукционную или модель истощения. Стартовые значения генерируются встроенным модулем программы, а затем, если необходимо, корректируются с учетом биологически правдоподобных значений. На первом этапе второй и последующих итераций берутся величины параметров и переменных, рассчитанные в ходе предыдущей итерации.
На втором этапе модельные и эмпирические (DATA) значения численности включаются в функцию правдоподобия (LIKELIHOOD) и вычисляется (like) мера их согласованности, то есть определяется вероятность того, что эмпирические значения могут быть получены с использованием данной биологической модели с заданными стартовыми значениями параметров и переменных.
На третьем этапе по формуле Байеса (BAYES, уравнение [18]) количественно оценивается способность модели с заданными параметрами (PRIORS) генерировать эмпирические значения DATA. В процессе расчетов происходит настройка параметров (PRIORS) в условиях, характеризуемых данными наблюдения (DATA), и рассчитываются новые апостериорные значения модельных параметров и переменных. Оцененные показатели параметров и рассчитанные модельные переменные, характеризующие модель в данный момент, играют роль начальных условий для следующей итерации.
Данная процедура расчета является заключительным этапом одного итерационного шага или звена в цепи Маркова (MCMC) и реализована с использованием метода Гиббса. В процессе итераций генерируются (stat) выборки распределений значений параметров и расчетных переменных. Статистический анализ таких выборок, в который входит расчет средних, ошибок средних, стандартных отклонений, медиан и доверительных интервалов параметров, является результатом прогона модели. Окончание итерационного процесса (прогона) происходит, когда ошибка среднего искомого параметра, рассчитанная в цепи Маркова, составит менее 5 % его стандартного отклонения (Spiegelhalter et al., 2000).
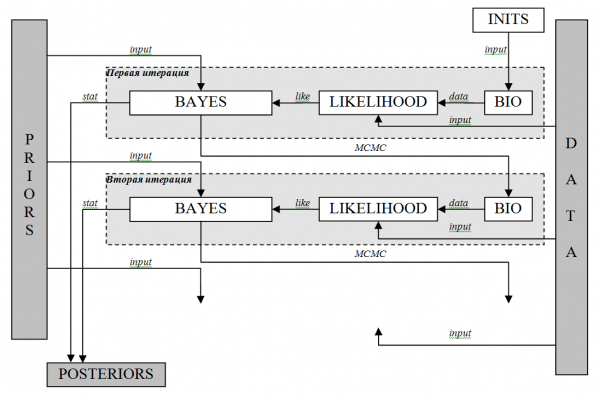
Рис. 2. Принципиальная блок-схема оценки параметров биологических моделей (показаны два итерационных шага). DATA – эмпирические данные; INITS – стартовые значения параметров и переменных; PRIORS – априорные распределения параметров; POSTERIORS – апостериорные распределения параметров и переменных; BIO – биологическая модель (уравнение популяционной динамики); LIKELIHOOD – функция правдоподобия; BAYES – формула Байеса; input – ввод данных; data – расчет численности животных по биологической модели; like – расчет правдоподобия; MCMC – переход к следующей итерации; stat – расчет апостериорных распределений параметров и переменных
Fig. 2. Schematic block diagram of the parameter estimates of biological models (shown in two iterative steps). DATA – empirical data; INITS – starting values of parameters and variables; PRIORS – a prior distribution of the parameters; POSTERIORS – the posterior distribution of parameters and variables; BIO – biological model (thq equation of population dynamics); LIKELIHOOD – likelihood function; BAYES – Bayes' formula; input – data input; data – calculation of the number of animals according to a biological model; like – the likelihood calculation; MCMC – the transition to the next iteration; stat – the calculation of posterior distributions of the parameters and variables
После итерационного прогона суммарная выходная статистика подвергалась анализу. Для оценки качества настройки модели выполнялось сравнение фактических значений и их апостериорных (рассчитанных в модели) распределений с использованием двух критериев согласия.
Во-первых, рассчитывались остатки, т. е. разности между логарифмами фактических индексов численности по съемке и рассчитанных индексов по модели. Чем лучше модель согласуется с данными, тем меньше величина остатков. Суммарная статистика отклонений (RSS, от residual sum of squares) показала степень смещения модельных значений от наблюдаемых всего временного ряда:
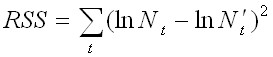 ,
,
где Nt – наблюдаемый индекс численности по съемке, N't – расчетный индекс численности по модели.
Во-вторых, адекватность модели анализировалась путем сравнения распределения каждой фактической величины со своим апостериорным прогнозным распределением (Gelman and Rubin, 1992). При этом после настройки параметров в модели имитируется набор наблюдаемых данных. Вероятности имитируемых значений фактических величин datarep имеют распределение:
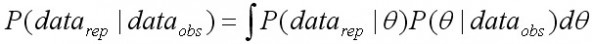 , [20]
, [20]
В выражении [20] показатель P(datarep |q ) представляет собой выборку наблюдений из распределений, рассчитанных в модели – P(q | dataobs).
Данный критерий проверяет, нет ли смещения наблюдаемого индекса численности относительно медианы распределения имитируемых на каждой итерации модели индексов численности. Степень отклонения суммируется в векторе p-значений, рассчитываемых как пропорция N-итераций, в которых выборка имитируемых данных наблюдения из апостериорного распределения превышает истинные значения данных наблюдения:
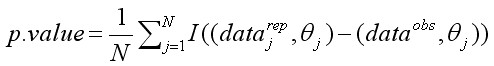 , [21]
, [21]
где I(x) = 1, если x истинно, и I(x) = 0, если x ложно. Величины, близкие к 1 или 0 в векторе p-значений, показывают, что набор фактических значений в значительной мере отклоняется от медианы апостериорного распределения. Величина p.value близкая к 0,5 показывает, что расчетная величина datajrep приблизительно в 50 % случаев больше входного значения и в 50 % – меньше, то есть отклонения не имеют систематического смещения.
За этапом оценки качества настройки параметров производится исследование моделируемой популяционной динамики, выясняется степень адекватности полученной модели. При этом оценивается поведение популяции при различных исходных предпосылках, например, меняются показатели степени эксплуатации, величины пополнения, уровня естественной смертности, продукционной способности популяции. Процесс исследования модели напрямую связан с конечной целью моделирования в нашей работе – определением популяционных параметров. В свою очередь показатели популяционных параметров являются основой для определения биологических и управленческих ориентиров при выработке стратегии рационального промыслового использования данной популяции.
Реализация модельных алгоритмов и статистическая обработка полученных результатов выполняется в программном продукте OpenBUGS, разработанном в Медицинском исследовательском центре в Кембридже (Spiegelhalter et al., 2000; OpenBUGS, 2009). Программа снабжена руководством пользователя, в котором подробно описан байесовский алгоритм пошаговой реализации математической модели, оценки параметров и диагностики.
Реализация байесовского подхода в оценке параметров модели
Рассмотрим методику применения байесовского подхода на примере оценки параметров продукционной модели Шефера, описанной выше уравнением [15]. С добавлением показателя вылова модель приобретает вид (Schaefer, 1954):
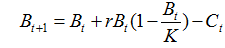
где Bt – численность в году t, Ct – вылов в году t, K – максимально возможная численность популяции и r – коэффициент мгновенного популяционного роста. Ненаблюдаемая переменная Bt может быть выражена через наблюдаемый показатель относительной численности (It), рассчитанный, например, по результатам исследовательской съемки:
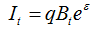
где q – коэффициент пропорциональности, в данном случае коэффициент улавливаемости, a 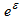
В системе уравнений [22] и [23] нужно оценить четыре параметра: r, K, q, 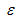
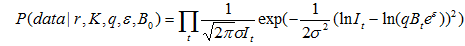
Функция правдоподобия определяет вероятность получения данных наблюдений (data) при определенном наборе параметров, значения которых соответствуют гипотезе H, то есть r, K, q,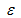
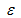
Обычно до начала оценки эксперт имеет, по крайней мере, приблизительное представление о возможных величинах параметров. Эти представления могут базироваться на информации, полученной из литературных источников или личного опыта эксперта. Рассмотрим ход рассуждений о возможной величине, например коэффициента улавливаемости q.
Отображая соотношение реальной величины численности и наблюдаемого индекса относительной численности, он может быть предварительно оценен посредством полевых экспериментов. Являясь коэффициентом пропорциональности для индекса численности, оцененной в ходе исследовательской съемки, этот показатель определяется, главным образом, уловистостью орудий лова. Доля пойманных животных из числа находящихся в зоне отлова, естественно, может принимать значения от 0 (никто не пойман) до 1 (отловлены все особи). На основании этой информации эксперт может допустить, что действительное значение коэффициента q равновероятно может находится в диапазоне от 0 до 1.
Допустим, что у эксперта имеется некая дополнительная информация в виде литературных данных о коэффициенте уловистости аналогичного трала по отношению к животным исследуемого нами вида. В результате он может прийти к выводу о том, что интервальная оценка коэффициента уловистости трала должна лежать, например, в пределах 0.4–0.6. Кроме того, из многолетнего опыта эксперта и литературных данных известно, что коэффициент уловистости варьирует от траления к тралению и зависит от множества факторов (параметров раскрытия трала, типа грунта, размеров животных и пр.). На основании этой информации, а также используя соображения о характере варьирования этого показателя, исследователь имеет некое мысленное представление о возможной величине этого параметра до начала моделирования процесса. Ожидается, что при использовании традиционного метода максимального правдоподобия и данных наблюдений, величина q окажется, скорее всего, близкой к 0.4–0.6. В тоже время маловероятно, что значение этого коэффициента будет близким, например, к 0 или к 1.
Чтобы избежать некорректной оценки q, очевидно, необходимо задать ее пределы, в которых будет проходить поиск оптимального решения. Такие пределы задаются, как правило, с учетом предыдущей накопленной информации, то есть априори (в данном случае на основании литературных данных и личного опыта эксперта). Для того чтобы использовать эту информацию, наше мысленное представление о возможной величине q необходимо выразить количественно. Задача заключается в построение частотного распределения вероятностей этой величины, которое называется априорным распределением параметра q.
Построение априорного распределения целесообразно начинать с выбора типа распределения. Однако на практике не всегда имеется исчерпывающая информация о том, какому закону подчиняется вероятностное распределение того или иного параметра. В настоящее время проблема выбора априорных распределений для параметров моделируемых биологических процессов освещена подробно (Kass, Wasserman, 1996; Punt and Hilborn, 1997). В данном случае, учитывая литературные данные, предполагаем, что распределение подчиняется нормальному закону с модой в интервале 0,4–0,6 и границами от 0 до 1. Графически такое распределение изображено на рисунке 7, а математически принято записывать как:
q~dnorm(0,50;50), [25]
где dnorm – нормальное распределение, а символ "~” обозначает “распределяется как”.
Параметры нормального распределения mu (среднее) и tau (точность, показатель обратно пропорциональный дисперсии, то есть 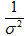
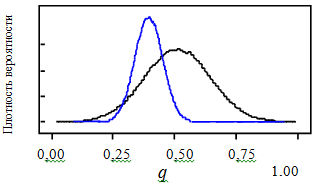
Рис. 3. Распределение вероятности параметра q (черная линия – априорное, синяя – апостериорное)
Fig. 3. Probability distribution of the parameter q (black line – a priori, blue – a posteriori)
Апостериорные распределения всегда находятся в границах своих априорных распределений. Степень отличия апостериорного от априорного распределения показывает, как много информации о значениях неизвестного параметра содержится в статистических данных наблюдений при условии, что априорное распределение было задано в широком диапазоне возможных значений. Чем выше и уже апостериорный пик, тем параметр точнее оценивается с помощью данных наблюдений. Если апостериорная вероятность слабо отличается от априорной, то, возможно, данные не несут полезной информации для корректировки первоначальной оценки параметра (рис. 3).
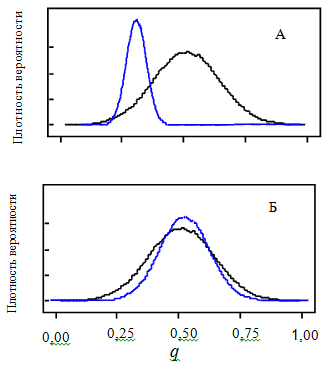
Рис. 4. Распределение вероятности параметра q (черная линия – априорное, синяя – апостериорное) при информативных (А) и малоинформативных (Б) данных наблюдений
Fig. 4. Probability distribution of the parameter q (black line – a priori, blue – a posteriori) for informative (A) and uninformative (B) observations+
Наиболее важным и одновременно сложным является вопрос выбора априорного распределения параметров. Для определенных параметров выбор может основываться в некоторых случаях на субъективном мнении эксперта. В идеале это мнение должно быть основано на фактах. Эти факты могут включать все те сведения, которые обычно не входят в формальный анализ количественных данных, а используются как информация, полученная вне эксперимента. Такая «внешняя» информация может включать:
1) результаты исследований по той же тематике;
2) результаты исследований, в которых изучались сходные биологические механизмы;
3) результаты лабораторных исследований, посвященные природе изучаемого явления;
4) результаты исследований, если эти результаты могут иметь ту же природу;
5) сведения о промежуточных исходах, которые наблюдались в данном эксперименте и свидетельствуют в пользу предложенной гипотезы;
6) информацию, полученную у других популяций со схожими биологическими и промысловыми параметрами.
Эти виды внешней информации предполагают ту или иную форму экстраполяции причинно-следственных связей. При этом параметр должен имеет априорное распределение, включающее значения искомого апостериорного распределения. На практике иногда желательно обрезать или укоротить апостериорные распределения с целью избежать растягивания процесса поиска решения. В таких случаях лимиты распределения должны быть выбраны в широких, биологически обоснованных пределах, чтобы не перекрывать апостериорное распределение. Целесообразно рассматривать несколько возможных априорных распределений различных параметров и анализировать результаты расчетов.
Согласно формулам [20] и [21] для настройки всего моделируемого процесса должны быть заданы априорные распределения не только для параметра q, но и для r, K, 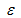
Рассмотренный пример байесовского подхода на примере продукционной модели представляет собой принципиальную схему оценки параметров модели. Реализация формулы Байеса, когда все параметры и расчетные переменные трактуются как случайные величины, основана на поиске решения системы интегральных уравнений. Процедура поиска решения связана с большим количеством вычислений и базируется на итеративном методе с применением генератора случайных чисел. В настоящей работе используется подход, который в англоязычной литературе известен как Markov Chain Monte Carlo (MCMC; Congdon, 2001). Этот алгоритм вычисления основан на построении цепи Маркова. Процесс, протекающий в системе, называется марковским, если для каждого момента времени которой вероятность любого состояния системы в будущем определяется только состоянием системы в настоящий момент и не зависит от того, каким образом система пришла в это состояние (Вентцель, 2003). Реализация цепи Маркова в численном виде происходит с помощью модели Гиббса (Gibbs sampler). Она обеспечивает способ выборки из совместных распределений многомерных переменных с помощью применения такого положения: для получения выборки из совместного распределения делаются многократно выборки из его представленных одномерных условных распределений. Процесс реализации MCMC с помощью модели Гиббса подробно описан в литературе (Gilks et al., 1996; Meyer, Millar, 2000).
Заключение
Байесовский подход к оценке параметров моделей популяционной динамики в настоящее время широко используются в промысловой биологии. Метод позволяет включать в алгоритм дополнительные знания в виде априорных распределений различных параметров, тем самым восполняя недостающие эмпирические данные. Вероятностные оценки также позволяют выполнять риск-анализ биологических и промысловых показателей состояния популяций, что делает модели полезными в принятии управленческих решений.
Оценка состояния запаса камчатского краба в Баренцевом море основывается на реализации традиционных методов определения продуктивности популяции. В основе оценки лежат основные постулаты теории рыболовства, в соответствии с которыми выполняется расчет популяционных параметров. В то же время биологические и экологические особенности камчатского краба и история его появления в Баренцевом море вынуждают отходить от алгоритмов, традиционно используемых при оценке запасов гидробионтов. Во-первых, трудность в определении возраста ракообразных не позволяет использовать преимущества моделей, основанных на оценке численности поколений. Во-вторых, характер роста численности искусственно созданной популяции затрудняет использование принципов управления, основанных на динамическом равновесии системы «окружающая среда – запас – промысел». В-третьих, на этапе начала промысловой эксплуатации запаса возникают трудности интерпретации связи биологических параметров популяции с промысловыми показателями. Кроме того, прямые наблюдения по результатам съемок и промысла несут значительное количество шума и зачастую весьма неопределенны, что связано как с методическими проблемами, так и с экологическими особенностями вида.
Моделирование популяционной динамики на основе байесовского подхода позволяет успешно решить ряд вышеуказанных проблем. Интегрирование данных, полученных в ходе различных исследований, в единую модель на основе байесовского метода оценивания параметров дает существенно более детальное описание изменений, происходящих в популяции. Точность оценки динамики при сравнительно низком качестве исходных данных становится зависимой в значительной степени от методов оценки параметров. Наиболее важным и одновременно сложным является вопрос выбора априорного распределения параметров. Для определенных параметров выбор может основываться в некоторых случаях на субъективном мнении эксперта. В идеале это мнение должно быть основано на фактах, которые могут включать сведения, которые обычно не входят в формальный анализ количественных данных, а используются как информация, полученная вне эксперимента или наблюдения.
Библиография
Бабаян В. К. Предосторожный подход к оценке общего допустимого улова (ОДУ): Анализ и рекомендации по применению. М.: Изд–во ВНИРО, 2000. 192 с.
Баканев С. В. Оценка запаса камчатского краба в Баренцевом море с использованием модели CSA // Камчатский краб в Баренцевом море . Гл. 4.2. Мурманск: Изд-во ПИНРО, 2003. С. 232–245.
Баканев С. В. Результаты применения стохастической когортной модели CSA для оценки запаса камчатского краба Paralithodes camtschaticus в Баренцевом море // Вопросы рыболовства. 2008. Т. 9. № 2 (34). С. 294–306.
Баканев С. В. Проблемы оценки запаса и регулирования промысла камчатского краба Paralithodes camtschaticus в Баренцевом море // Вопросы рыболовства. 2009. Т. 10. № 1 (37). С. 51–63.
Баранов Ф.И. К вопросу о биологических основаниях рыбного хозяйства // Изв. отдела рыбоводства и науч.-промысл. исслед. 1918. Т. 1. Вып. 1. С. 84–128.
Васильев Д. А. Когортные модели и анализ промысловых биоресурсов при дефиците информационного обеспечения . М.: Изд–во ВНИРО, 2001. 111 с.
Вентцель Е. С. Теория вероятностей . М.: Издательский центр «Академия», 2003. 576 с.
Одум Ю. Экология: В 2–х т. Т. 2. М.: Мир, 1986. 376 с.
Рикер У. Е. Методы оценки и интерпретация биологических показателей рыб . М.: Пищевая промышленность, 1979. 408 с.
Шибаев С. В. Промысловая ихтиология . СПб: Проспект Науки, 2007. 400 с.
Adkison M. D. and R. M. Peterman. 1996. Results of Bayesian methods depend on details of implementation: An example of estimating salmon escapement goals. Fish. Res. 25, Alaska crabber call for fleet cut // World Fish. 1997. Vol. 46. N7. P. 155–170.
Annala J. H. Fishery assessment approaches in New Zealand's ITQ system. // Proceedings of the International Symposium on Management Strategies for Exploited Fish Populations, Alaska Sea Grant Coll. Program Rep. No 93–02, University of Alaska, Fairbank, 1993. P. 791–805.
Adkison M. D., R. M. Peterman. 1996. Results of Bayesian methods depend on details of implementation: An example of estimating salmon escapement goals. Fish. Res. 25, Alaska crabber call for fleet cut // World Fish. 1997. Vol. 46. N7. P. 155–170.
Annala J. H. Fishery assessment approaches in New Zealand's ITQ system. // Proceedings of the International Symposium on Management Strategies for Exploited Fish Populations, Alaska Sea Grant Coll. Program Rep. No 93–02, University of Alaska, Fairbank, 1993. P. 791–805.
Angel J. R., Burke D. L., O'Boyle R. N., Peacock F. G., Sinclair M., Zwanenburg K. C. T. Standardization of nomenclature for animal health risk analysis. // Rev. Sci. Tech. O.I.E. 1994. Vol. 12. P. 1045–1053.
Balsiger J. W. A computer simulation model for the eastern Bering Sea king crab. Ph. D. dissertation, Seattle: University of Washington, 1974. 47 p.
Bayes T. An essay towards solving a problem in the doctrine of chances. Philosophical Transactions of the Royal Society. 1763. 330–418. (Reprinted in: Biometrica (1958). № 45. P. 293–315.
Burgner R. L. Life history of sockeye salmon (Oncorhynchus nerka). In: Groot, C. and L. Margolis. eds. Pacific salmon life histories, Vancouver: University of British Columbia Press. 1991. 118 p.
Butterworth D. S., Punt A. E. On the Bayesian approach suggested for the assessment of the Bering-Chukchi-Beaufort Seas stock of bowhead whales // Rep. int. Whal. Comm. 1995. Vol. 45. P. 303–311.
Cadrin S. X. Evaluation two assessment methods for Gulf of Maine northern shrimp based on simulations // J. Northw. Atl. Fish. Sci. 2000. Vol. 27. P. 119–132.
Collie J. S. Estimating of abundance of king crab populations from commercial catch and research survey // Report to the Alaska Department of Fish and Game, University of Alaska Fairbanks, Juneau Center for Fisheries and Ocean Sciences, Juneau. 1991. Rep. №. 91–03. P. 134–162.
Congdon P. Introduction to Bayesian statistical modeling. London: Wiley, 2001. 556 p.
Drury K. L. S., Drake J. M., Lodge D. M., Dwyer G. Immigration events dispersed in space and time: Factors affecting invasion success // Ecological Modelling. 2007. Vol. 206. Issues 1-2. P. 63–78.
Gelman A., Rubin D. B. Inference from iterative simulation using multiple sequences. Statistical Science. 1992. Vol. 7. P. 457–511.
Gulland J. A. Estimation of mortality rates. Annex to Arctic fisheries working group report ICES C.M. 1965. D: 3. (mimeo). In P.H. Cushing (ed). Key papers on fish populations. Oxford. IRL Press. 1983. Reprinted as p. 1965. P. 231–241.
Haddon М. Modelling and quantitative methods in fisheries. Washington: Chapman & Hall / CRC, 2001. 406 p.
Hilborn R., Walters C. J. Quantitative Fisheries Stock Assessment: Choice, Dynamics and Uncertainty. New York: Chapman & Hall, 1992. 570 p.
ICES Report of the Working Group on Nephrops Stocks. ICES CM 2001/ACFM:16, 2001a. 325 p.
ICES Report of the Pandalus Assessment Working Group. ICES CM 2001/ACFM:04. 2001b. 354 p.
ICES Report of the Arctic Working Group. ICES CM 2008/ACFM:06. 2005. 355 p.
Jones R. Assessing the long–term effects of changes in fishing efforts and mesh size from length composition data // ICES. C. M. 1974. 33 p.
Hvingel C., Kingsley M. C. S. A framework to model shrimp (Pandalus borealis) stock dynamics and quantify risk associated with alternative management options, using Bayesian methods. // ICES J. Mar. Sci. 2006. Vol. 63. P. 68–82.
Haddon М. Modelling and quantitative methods in fisheries. Chapman & Hall/CRC Washington, D.C. 2001. 406 p.
Hilborn R., Walters C. J. Quantitative Fisheries Stock Assessment: Choice, Dynamics and Uncertainty. New York: Chapman & Hall, 1992. 570 p.
Kass R. E., Wasserman L. The selection of prior distributions by formal rules // Journal of the American Statistical Association. 1996. Vol. 91. P. 1345–1370.
Kinas P. G. Bayesian fishery stock assessment and decision making using adaptive importance sampling // Can. J. Fish. Aquat. Sci. 1996. Vol. 53. P. 414–423.
Kruse G. H., Collie J. S. Preliminary application of a population size estimation model to the Bristol Bay stock of red king crabs. Alaska Department of Fish and Fame, Division of Commercial Fisheries, Juneau, Alaska. Regional Information Report. 1991. № 5J91–09. 25 p.
McAllister M. K., Kirkwood G. P. Bayesian Stock assessment: a review and example application using the logistic model. ICES Journal of Marine Science. 1998. Vol. 55. P. 1031–1060.
Meyer R., Millar R. B. Bayesian stock assessment using a state–space implementation of the delay difference model // Can. J. Fish. Aquat. Sci. 1999. Vol. 56. P. 37–52.
Millar R. B., Meyer R. Bayesian state-space modeling of age-structured data: fitting a model is just the beginning. Can. J. Fish. Aquat. Sci. 2000. Vol. 57. P. 43–50.
Murphy G. I. A solution of the catch equation. J. Fish. Res. Bd. Can. 1965. Vol. 22. P. 191–202. OpenBUGSб 2009. URL: http://www.openbugs.info (дата обращения 10.09.2012).
Patterson K. R. Evaluating uncertainty in harvest control law catches using Bayesian Markov chain Monte Carlo virtual population analysis with adaptive rejection sampling and including structural uncertainty // Can. J. Fish. Aquat. Sci. 1999. Vol. 56. P. 208–221.
Pope J. G. An investigation of the accuracy of virtual population analysis using cohort analysis. Int. Comm. Northwest Atl. Fish. Res. Bull. 1972. Vol. 9. P. 65–74.
Punt A., Hilborn R. Fisheries stock assessment and decision analysis: the Bayesian approach. Reviews in Fish Biology and Fisheries. 1997. Vol. 7. P. 35–63.
Punt A. E., Hilborn R. BAYES–SA – Bayesian Stock Assessment Methods in Fisheries – User's Manual // School of Aquatic and Fishery Sciences University of Washington Seattle, Washington. 2001. 228 p.
Punt, A.E., Butterworth D. S. Further remarks on the Bayesian approach for assessing the Bering–Chukchi–Beaufort Seas stock of bowhead whales. Rep. int. Whal. Commn. 1996. Vol. 46. P. 481–491.
Quinn T. J., Turnbull C. T., Fu C.. A Length-Based Population Model for Hard-to-Age Invertebrate Populations // Fishery Stock Assessment Models. Alaska Sea Grant College Program Report. AK–SG–98–01. University of Alaska Fairbanks, 1998. P. 531–556.
Schaefer M. B. A study of the dynamics of the fishery for yellowfin tuna in the eastern tropical Pacific Ocean // Bull. Inter-Am. Trop. Tuna Comm. 1957. Vol. 1. P. 25–56.
Schnute J. T. A General Framework for Developing Sequential Fisheries Models // Can. J. Fish. Aquat. Sci. 1994. Vol. 51. P. 1676–1688.
Schnute J. T., Richards L. J., Olsen N. Statistics, Software, and Fish Stock Assessment // Fishery Stock Assessment Models. Alaska Sea Grant College Program Report. AK–SG–98–01. University of Alaska Fairbanks, 1998. P. 171–184.
Smith M. T., Addison J. T. Methods for stock assessment of crustacean fisheries // Fisheries Research. 2003. Vol. 65. P. 231–256.
Spiegelhalter D. J., Thomas A., Best N. WinBUGS version 1.3 User Manual. MRC Biostatistics Unit, Inst. of Public Health, Cambridge, England. 2000. 167 p.
Sullivan P. J., Lai H. L., Gallucci V. F. A catch–at–length analysis that incorporate a stochastic model of growth // Can. J. Fish. Aquat. Sci. 1990. Vol. 47. P. 184–198.
Weber D. D., Miahara T. Growth of the adult male king crab, Paralithodes camtschatica (Tilesius) // Fish. Bull. U. S. 1962. Vol. 62. P. 53–75.
Zheng J., Murphy M. C., Kruse G. H. A length–based population model and stock–recruitment relationships for red king crab, Paralithodes camtschaticus, in Bristol Bay, Alaska. // Can. J. Fish. Aquat Sci. 1995. Vol. 52. P. 1229–1246.
Zheng J., Murphy M. C., Kruse G. H. Application of a Catch–Survey Analysis to Blue King Crab Stocks Near Pribilof and St. Matthew Islands // Alaska Fishery Research Bulletin. 1997. Vol. 4 (1). P. 62–74.






 © 2011 - 2026
© 2011 - 2026