Введение
Сложные системы, в отличие от простых, имеют большое число взаимосвязанных качеств. Поэтому аналитические модели отдельных их качеств не адекватны им, а имитационные модели достаточно большой совокупности их качеств весьма сложны [1] и недостаточно общи.
| [1] Пионеры кибернетики, мексиканский физиолог и врач А. Розенблют (Arturo Rosenblueth Stearns; 1900–1970) и американский математик Н. Винер (Norbert Wiener; 1894–1964), ввели в обиход такой образ: «The best material model for a cat is another, or preferably the same cat – Лучшая материальная модель для кошки – это другая, а лучше та же кошка» (Rosenblueth, Wiener, 1945, с. 320). |
Три парадигмы (учения) «правят миром» (на рис. 1 схематично представлены три парадигмы познания мира (Розенберг, 2022, с. 36)). Первая – лапласовский детерминизм (полная определенность поведения объектов живой природы) – уверенность в том, что все происходящее имеет причину в человеческом понятии и есть непознанная разумом необходимость (на принципе детерминизма построена, например, классическая физика (механика)). Вторая – случайность, стохастизм (вероятностная определенность поведения объектов живой природы). Математически это означало необходимость развития теории вероятностей (процесс задается функцией распределения). Имеет место и третья парадигма, которая начала складываться во второй половине ХХ в., – хаос-самоорганизация (неопределенность в динамике поведения объектов живой природы). Приняв ту или иную парадигму, мы неизбежно попадаем в одну из ситуаций, представленных на рис. 1.
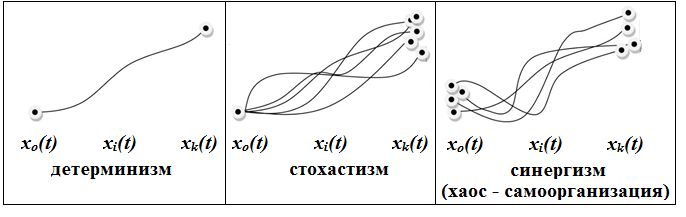
Рис. 1. Соотношение векторов состояния сложных систем
для трех парадигм познания мира
Fig. 1. The ratio of state vectors of complex systems for three paradigms of world cognition
Становление математической теории динамики популяций началось с допущения о равномерности распределения особей популяции по пространству (плотность популяции одинакова во всех точках ареала). Очевидно, что это «слишком сильное» утверждение, и природным популяциям свойственна мозаичность структуры в пространстве (Розенберг, 2013). Кроме того, пространственная гетерогенность дополняется и временной неоднородностью – распределение первоначально возникшей флуктуации популяционной плотности по ареалу (этот процесс называют распространением популяционных волн (Свирежев, 1987)). Примером такого совместного «действия» временной и пространственной динамики могут служить вспышки численности и опустошительные налеты саранчи (Schistocerca gregaria, Locusta migratoria, Nomodacris septemfasciata и др.) на посевы сельскохозяйственных культур в Африке и Азии. Так, например, область, в пределах которой встречаются стаи N. septemfasciata (Serville, 1839), в 1500 (!) раз превышает по площади область постоянного обитания одиночной фазы этого вида (см.: Гиляров, 1990, с. 110).
Все виды живых организмов в природе представлены не отдельными особями, а в форме совокупностей числа (иногда очень большого) особей-популяций. Это положение предложено С. С. Четвериковым в 1903 г. Можно выделить следующие типы размещения особей в пространстве (по осям стохастичность-детерминированность и равномерность-неравномерность (Миркин, Розенберг, 1978; Розенберг и др., 1999, с. 198; см. рис. 2):
- детерминированное равномерное (а; регулярное – распределение достаточно высоких деревьев в лесу, кроны которых образуют часть общего полога или искусственные лесопосадки);
- стохастическое равномерное (b; случайное – распределение моллюска Mulinia lateralis (Say, 1822) в илистых наносах приливной зоны (Jackson, 1968));
- детерминированное неравномерное (с; ложноконтагиозное – «гнездовые посадки леса»);
- стохастическое неравномерное (d; контагиозное – распределение лабазника обыкновенного (Filipendula vulgaris Moench, 1794) на остепненных лугах Южного Урала (Миркин, Розенберг, 1977)).
Принцип агрегации особей Олли (Миркин и др., 1989; Реймерс, 1990; Stephens et al., 1999) – скопление особей популяции, с одной стороны, усиливает конкуренцию между ними за пищевые ресурсы и жизненное пространство, с другой – приводит к повышению способности группы в целом к выживанию. Таким образом, как «перенаселенность», так и «недонаселенность» может выступать в качестве лимитирующего фактора. Так, группа растений способна более эффективно противостоять ветру или уменьшать потери воды, чем отдельные особи, а с другой стороны, в группе усиливается конкуренция за свет и элементы минерального питания (Одум, 1986). Принцип сформулирован американским экологом У. Олли (Warder Clyde Allee; 1885–1955) в 1931 г.
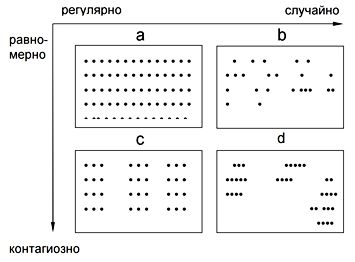
Рис. 2. Схема типов размещения особей в пространстве
(пояснения в тексте)
Fig. 2. Scheme of distribution types of individuals in space (explanations in the text)
Большое число примеров возникновения мозаичности (агрегированности особей и неоднородностей горизонтального сложения растительных сообществ) приводится Дж. Харпером (Harper, 1973) и Т. А. Работновым (1983, с. 161–166). Назовем и интересное теоретическое построение – «модель карусели», предложенную в 1991 г. Э. Ван-дер-Маарелем [2] (см.: Миркин, Наумова, 1994, 1998). Суть ее сводится к мелкомасштабным циклическим изменениям состава растительных сообществ в «ценомолекулах», что обеспечивает стабильность видового состава всего сообщества. При этом по характеру поведения видов в «карусели» различают
- устойчивые «виды-наседки» (англ. sitter),
- «партизаны» (англ. guerilla) с малым радиусом «нападения» на окружающее «ценомолекулу» сообщество (например, Hypericum maculatum),
- виды, способные перемещаться на значительное расстояние (Achiellea millefolium, Poa pratensis) и
- «виды гибкие» (англ. phalanx; Nardus stricta, Festuca rubra и др.).
| [2] Э. Ван-дер-Маарель (Evert "Eddy" van der Maarel; 1934–2021) – датский эколог, фитоценолог. |
Механизмами формирования пространственной неоднородности в размещении особей популяции растений могут быть расселение семян, спор и пр., особенности разрастания доминанта (папоротник-орляк Pteridium aquilinum (L.) Kuhn, 1879), изменение содержания питательных веществ в почве, влияние суточных и сезонных изменений погодных условий, локальные различия в местообитаниях и др. (Одум, 1986). Все это привело к возникновению и развитию концепции метапопуляций.
Метапопуляция – это пространственно структурированная популяция (d на рис. 2), которая сохраняется во времени как набор локальных взаимодействующих популяций с ограниченным расселением между ними (см., например: Салменкова, 2018). Сам термин «метапопуляция» был введен Р. Левинсом [3] (Levins, 1969) для описания модели динамики численности насекомых-вредителей сельскохозяйственных посевов (модель «популяции популяций»), хотя сама эта идея широко обсуждалась применительно к видам в естественных или искусственно фрагментированных средах обитания. У нас в стране эти представления наиболее последовательно развивал С. С. Шварц (1963, 1965, 1967, 1968 и др.). «Непременное условие поддержания жизнеспособности популяции в изменяющихся условиях среды – высокая степень ее генетической разнородности. Поддержание генетической разнородности популяций обеспечивается экологическими механизмами (различный образ жизни разных внутрипопуляционных групп животных, <…> и др.). <…> Динамика пространственной структуры популяций (или группы смежных популяций) – один из важнейших механизмов приспособления вида к изменяющимся условиям среды. Сложная пространственная структура страхует популяцию от случайного обеднения ее генофонда, и, вместе с тем, создает условия для быстрого приспособительного преобразования ее генетической структуры (выделено нами. – Авторы)» (Шварц, 1973, с. 55, 58). А вот более раннее высказывание (Шварц, 1968, с. 61): «Перехожу к рассмотрению экологических механизмов эволюционного процесса, основанных на преобразовании не возрастной, а пространственной структуры популяций. В природе популяции представлены относительно мелкими структурными единицами (я называю их микропопуляциями), которые существуют самостоятельно в течение непродолжительного периода, а затем объединяются в единую крупную популяцию. Хорошо изученные механизмы, основанные преимущественно на поведенческих реакциях животных, временно изолируют внутрипопуляционные группы особей даже в тех случаях, когда никаких физических преград между ними нет. Достаточно сказать, что мыши подвала и чердака двухэтажного дома или двух соседних домов представляют собой временно изолированные поселения. Это приводит к возникновению генетических различий между соседними поселениями животных». И еще одна цитата: «Под экологической структурой популяции понимают определенное соотношение возрастных групп, определенное соотношение полов, сочетание оседлых животных с животными-мигрантами, наличие семейных, стадных и т.п. группировок. Чем сложнее структура популяции, тем выше ее приспособительные возможности... Единство приспособительных реакций популяций осуществляется с помощью сложной системы сигнализации и связи, информирующей отдельных особей о состоянии популяции в целом. Эта система информации основана на экологических и физиологических реакциях животных на внешние стимулы самой различной природы (химические, изменение внешней среды, изменение частоты и степени внутрипопуляционных контактов, звуковые и зрительные сигналы и т. п. – Авторы). Совокупность этих реакций спаивает особей популяции в единую функционирующую систему, обеспечивающую поддержание численности вида в разнообразной среде обитания» (Шварц, 1969, с. 14–15).
| [3] Р. Левинс (Richard "Dick" Levins; 1930–2016) – американский математический эколог, генетик, популяционный биолог. По иронии судьбы он был заинтересован в контроле численности насекомых (их уничтожении), а не в сохранении популяций. |
В развитие концепции метапопуляций можно рассматривать и такие представления Ю. М. Свирежева (1987, с. 12): «Любая особь популяции в процессе своей жизнедеятельности перемещается по ареалу – имеет свой радиус индивидуальной активности. Это понятие было впервые введено Н. В. Тимофеевым-Ресовским ((Timofeeff-Ressovsky, 1940). – Авторы), а сам радиус может быть измерен экспериментально. <…> Заметим, что если этот радиус больше, чем характерный размер ареала, то популяцию можно считать хорошо перемешанной и при ее описании можно не учитывать пространственных эффектов. Если же мы имеем обратную картину, то рассмотрение пространственного распределения популяции становится просто необходимым».
Аналитическая модель, построенная на основе небольшого числа достаточно правдоподобных гипотез, полностью находится в руках исследователя. Ее качественный анализ, проводимый без использования ЭВМ (или, в крайнем случае, ЭВМ выступает в качестве «большого арифмометра», облегчающего только численное решение модели), претендует на выполнение объяснительной функции теории моделируемого класса систем. А так как эта функция является одной из наиболее важных, то многие исследователи считают, что аналитические модели и представляют собой собственно математическую теорию изучаемых объектов. Компактность представления имеющейся информации – это одна из наиболее сильных сторон аналитического моделирования (Розенберг, 2013).
В точечных моделях параметры меняются только по одной переменной (например, во времени или по координате (экоклин, топоклин)); такие модели чаще всего имеют вид обыкновенных дифференциальных уравнений. В моделях с распределенными параметрами параметры меняются по двум и более переменным, такие модели имеют вид уравнений в частных производных. При математическом моделировании метапопуляционных процессов учитываются пространственные изменения, что влечет за собой применение моделей с распределенными параметрами. Но и точечные модели могут описывать некоторые элементы неоднородности распределения популяций по пространству.
Аналитический обзор
Точечные модели
Одна из основных задач структурной организации популяций – это описание механизмов формирования агрегаций особей (пространственно структурированная популяция). Эта задача возникла давно, но наиболее образно она сформулирована в незаслуженно забытой научно-популярной брошюре Г. Дохман-Гармиза (1927, с. 11–12): «Вы сталкиваетесь, быть может, с этим явлением (агрегация особей. – Авторы) иногда в такой форме. Вас привлекают издали заросли белого поповника (Leucanthemum vulgare Lam. (1779); или какого-нибудь другого цветка). Направляясь к ним, вы по дороге наталкиваетесь на эти растения и, собирая цветы, непрерывно нагибаетесь. Когда собран большой букет поповника, и вы начинаете чувствовать уже некоторую усталость – перед вами впервые появляется заросль белых, прекрасных больших цветов поповника. Так и сверкают на солнце белые лепестки и желтые серединки! Вы сравниваете их с вашим букетом, и невольно становится обидно. Нарвали букет мелких корявых поповников, устали, а вот здесь только бы и начинать собирать. Если вы предприимчивы и не падаете духом, – букет летит в сторону, и вы собираете новый». Иными словами, в условиях внутривидовых взаимодействий наблюдается эффект улучшения условий жизни популяции.
Классическая модель системы «хищник – жертва»:

где х – количество жертв, y – количество хищников, t – время, α, β, γ, δ – коэффициенты, отражающие взаимодействия между видами (все положительны); стационарной точкой этой системы уравнений является ![]() ; эта стационарная точка устойчива, является центром, в ее окрестности происходят гармонические колебания численности обеих популяций с частотой
; эта стационарная точка устойчива, является центром, в ее окрестности происходят гармонические колебания численности обеих популяций с частотой ![]() (Ризниченко, Рубин, 2004).
(Ризниченко, Рубин, 2004).
Пусть имеется некоторая неоднородность пространства – «укрытие», где может сохраняться часть популяции жертвы. Так, усложняя опыты по экспериментальному подтверждению теоретической модели (1), Г. Ф. Гаузе (Gause, 1934) устраивал убежище для жертвы, используя в качестве питательной среды овсяный отвар с «осадком» и «без осадка» или внося в пробирки с инфузориями немного стеклянной ваты. Среди нитей ваты могли свободно перемещаться жертвы-парамеции (Paramecium caudatum), но не могли хищники-дидиниумы (Didinium nasutum). В таком варианте опыта дидиниум съедал всех парамеций, плавающих в свободной от ваты части пробирки, и вымирал, а популяция парамеции затем восстанавливалась за счет размножения особей, уцелевших в убежище. Некоторого подобия колебаний численности хищника и жертвы Гаузе удалось добиться только в том случае, когда он время от времени вносил в культуру и жертву, и хищника, имитируя таким образом иммиграцию. Еще один пример «укрытия». Рыбаки на озере Балатон (Венгрия) с успехом ловили «крупную плотву в заводи, образованной нерабочим паромом, который стоял у берега залива, а вдоль этого берега бежало течение от впадающей речушки. Видимо, плотва в заводи находила укрытия от хищника, так как между бортом и берегом в одном месте выросла целая плантация густых водорослей. А на водорослях, очевидно, очень интенсивно развивались водяные организмы, которые служили рыбе кормом» (Антонов, Горяйнов, 2010, с. 202).
Этот эффект легко учитывается в модели (1), например, следующим образом (Базыкин, 2003):
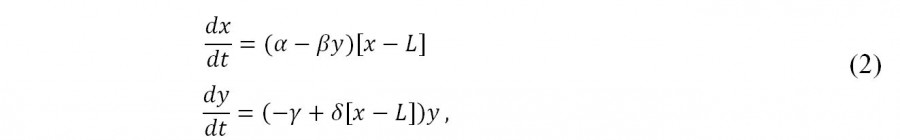
где L – это часть популяции жертвы, сохраняющейся в «укрытии»; стационарной точкой этой системы уравнений является ![]() , (если L = 0 (т. е. нет укрытия), то особая точка уравнения (2) совпадает с особой точкой уравнения (1).
, (если L = 0 (т. е. нет укрытия), то особая точка уравнения (2) совпадает с особой точкой уравнения (1).
Детерминированные модели с распределенными параметрами
Билокальная популяционная модель «эффекта Олли» (Домбровский, Маркман, 1983, с. 78–80; Розенберг и др., 1999) – модель конкуренции с учетом диффузионного обмена между двумя идентичными по своим экологическим характеристикам местообитаниям. Модель описывает некоторые качественные закономерности распределения и пространственной структурированности (агрегированности) популяций в предположении, что перемещение особей в пространстве подчиняется простейшему диффузионному закону:
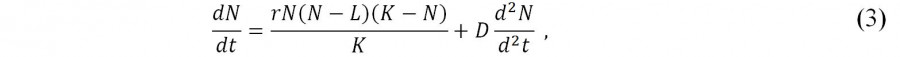
где L – нижняя критическая численность популяции; К – емкость среды; D – коэффициент диффузии, определяемый подвижностью особей (например, в рамках модели «карусели» Э. Ван-дер-Маареля). В этой формулировке ограниченное, устойчивое, пространственно неоднородное решение данного уравнения носит название «диссипативной структуры» (Пригожин, 1985) – состояние, обладающее пространственной и временной упорядоченностью, в организации которой принимает активное участие процесс диффузии (физический смысл такой структуры «состоит в незамкнутости системы, подкачке в нее энергии извне» (Домбровский, Маркман, 1983, с. 8)). Заметим, что Ю. М. Свирежев (1987, с. 144), сохраняя в экологии понятие «диссипативная структура», хорошо известное в химии, теории морфогенеза, неравновесной термодинамике, считает, что «более правильно было бы их называть пространственно неоднородными стационарными структурами».
Проведенный анализ (Домбровский, Маркман, 1983; Свирежев, 1987) показал, что при малом коэффициенте диффузии D в вольтерровской модели (3) существуют две точки устойчивого равновесия, в одной из которых плотность особей стремится к насыщению, а в другой происходит вымирание. С ростом D наблюдается выравнивание распределения, и диссипативная структура исчезает. В рамках модели «карусели» этот результат описывает пространственно-временное изменение «видов-партизан».
Модель «цветения воды». В моделях с распределенными параметрами переменные зависят от пространственных координат и описываются дифференциальными уравнениями с частными производными. В качестве примера рассмотрим аналитическую модель сезонного развития сообщества фитопланктона (т. н. эффект «цветения воды»), которое также имеет пространственно-колебательный характер (Крестин, Розенберг, 1996, 2002; Rozenberg, Krestin, 1997).
Модель вольтерровского типа предполагает конкурентные взаимоотношения «обычных» (x1) и синезеленых водорослей (x2), причем последние находятся под воздействием зоопланктона (z). Предполагается, что:
- коэффициенты экспоненциального роста обычных и синезеленых водорослей прямо пропорциональны концентрации фосфора (Р);
- количество погибшего зоопланктона, за исключением естественной смертности, прямо пропорционально концентрации зоопланктона и концентрации тяжелых металлов в воде (М);
- количество сбрасываемого в воду фосфора за единицу времени постоянно и равно ξP;
- количество фосфора, потребляемого обоими видами водорослей, прямо пропорционально их концентрациям и плотности фосфора;
- относительно тяжелых металлов делаются аналогичные допущения (количество сбрасываемых тяжелых металлов в единицу времени постоянно – ξМ);
- коэффициент ε2 зависит от температуры (Т) следующим образом:
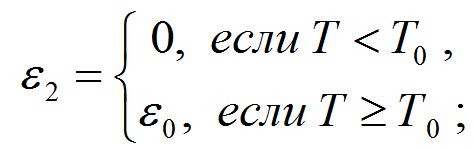
- выполняется «гипотеза эквивалентов» (Вольтерра, 1976) – биомасса жертвы полностью перерабатывается в биомассу хищника.
Эти предположения позволяют записать следующую систему уравнений для анализа феномена «цветения воды»:
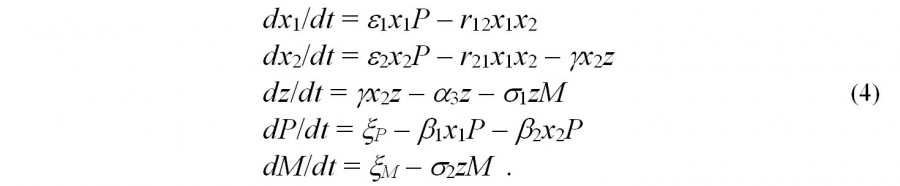
Эта система имеет два стационарных решения, устойчивость которых зависит от соотношения ее коэффициентов (Крестин, Розенберг, 1996). Результаты моделирования хорошо согласуются с эмпирическими данными: было отмечено наличие двух пиков «цветения» (весеннего и летнего) для x2 и z что хорошо согласуется с результатами полевых наблюдений (см., например, данные по фитопланктону для сезонов 1989–1991 гг. в Приплотинном плесе и 1982 г. в Ульяновском плесе Куйбышевского водохранилища (Паутова, Номоконова, 1994, с. 70) и по зоопланктону – в частности, биомассе коловраток (Тимохина, 2000, с. 60)).
Наблюдения гидробиологов (см., например: Жариков, 1998; Фитопланктон Нижней Волги..., 2003, с. 54, 56, 70) свидетельствуют о том, что для «широких» и «длинных» водохранилищ (таких, как, например, Куйбышевское) имеет место феномен, который можно определить как «волну цветения» по пространству водохранилища (не только «сверху – вниз», но и от одного берега к другому). Для объяснения этого явления рассмотрим следующую модель, в которой учитывается пространственная неоднородность при описании периодических изменений сообществ альгофлоры в водохранилищах.
Рассмотрим квадрат [0, Y]•[0, Y]. Уравнение переноса и турбулентной диффузии гидрозоля (в двухмерном варианте и при постоянном коэффициенте диффузии D) имеет следующий вид (Марчук, 1989):
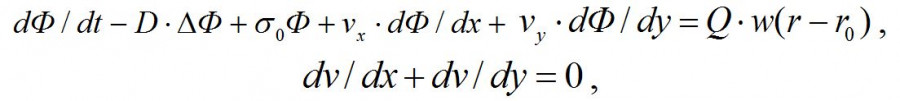
где Ф – концентрация загрязняющего гидрозоля, Q – мощность источника, w(r – r0) – функция источника, r = r(x,y), r0 – точка предполагаемого сброса, v – скорость течения по координатам х и y. Будем считать, что сброс гидрозоля идет с берегов водоема равномерно по всей их длине [0, Y]. Тогда функция источника имеет вид:
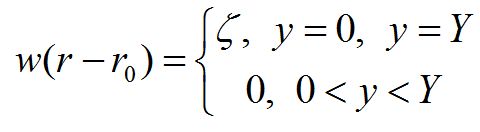
Каждое уравнение «точечной» модели «цветения воды» (4) можно дополнить членами вида:
![]()
где D – коэффициент турбулентной диффузии, v – скорость течения в водохранилище; вместо xi в соответствующих уравнениях системы будут стоять z, P, M. При определенных граничных и начальных условиях и соотношении коэффициентов, а также при четырех режимах сброса Р и М в водоем (равномерно вдоль берегов, разные варианты равномерного и «точечного» сброса (Крестин, Розенберг, 2002)) получается режим «волны цветения» по длине водохранилища (рис. 3).

Рис. 3. Зависимость концентрации синезеленых водорослей (а) и концентрации фосфора (б)
от пространственных координат при значении времени t = 90 сут
Fig. 3. Dependence of the concentration of blue-green algae (a) and the concentration of phosphorus (б) on spatial coordinates at a time value of t = 90 days
На этих рисунках хорошо виден процесс появления и движения волны «цветения воды», который согласуется с интуитивными представлениями специалистов-гидроэкологов. Заключенный в модель механизм несколько отличается от принятого в гидробиологии (в основном только через воздействие биогенов (Эдмондсон, 1998)) в сторону большей «реалистичности», что делает модель полезной как для целей объяснения наблюдаемых феноменов, так и для синтеза на ее основе прогнозирующих имитационных моделей.
Модель пространственно-временной динамики популяции с возрастной структурой и дальнодействующими взаимодействиями. Еще один, более сложный вариант модели пространственно-временной динамики популяции исследован в работе М. П. Кулакова и Е. Я. Фрисмана (2018, 2019). Рассмотрен подход к построению и исследованию модели с дискретным временем и дискретным пространством, предназначенной для описания и исследования пространственно-временной динамики двухвозрастной популяции, проживающей на двумерном ареале (структурированной метапопуляции). При этом полагается, что особи разных поколений взаимодействуют между собой и мигрируют на большие расстояния (миграция особей возможна в некоторой окрестности, а интенсивность потока мигрантов падает с удалением от субпопуляции). Авторы изучили условия формирования групп синхронных популяций (или кластеров), образующих в пространстве структуры типа пятен или полос, перемешанных с уединенными состояниями. Динамика последних «вполне вписывается в термин "вспышка массового размножения", характерного для некоторых насекомых (например, для сибирского шелкопряда, саранчи и др.)» (Кулаков, Фрисман, 2019): уединенные состояния характеризуются быстрым нарастанием численности одиночной субпопуляции, после которого следует резкий спад. Кроме того, по результатам моделирования такие «вспышки» происходят когерентно на других территориях, что создает принципиальную возможность прогноза таких явлений.
Имитационные модели. Индивидуально-ориентированное моделирование
По одной из возможных классификаций моделей сложных систем (Розенберг, 2013) выделяют «класс» имитационных моделей (англ. simulation) (Шеннон, 1978; Лоу, Кельтон, 2004). М. Страшкраба [4] на конференции по моделированию водных систем, проходившей в Праге в 1992 г., так охарактеризовал имитационное моделирование (цит. по: Меншуткин, 2010, с. 357): «Имитация систем есть специфическая форма процесса познания. Предметом имитации могут быть системы реально существующие, проектируемые или даже не имеющие непосредственного отношения к реальности. Основной принцип имитации систем – получение суждений об имитируемой системе при помощи экспериментов с моделью. Именно эксперименты с моделью отличают имитацию от других форм познания». В имитационном моделировании существует несколько парадигм (постановок проблем и подходов к их решению, используемых в качестве «каркаса» при построении и анализе моделей). Чаще всего выделяют четыре достаточно различные системы взглядов: динамические системы, системная динамика, дискретно-событийное моделирование, мультиагентные модели (Борщёв, 2007; Розенберг, 2013). Эти парадигмы различаются не столько областями применения, сколько концепциями и взглядами на проблему, подходами к ее решению. «Очень часто приверженцы одной парадигмы считают, что "правильные" постановка и решение проблем имитационного моделирования возможны только в рамках концепций и методик именно этой парадигмы. <…> В действительности, каждая из парадигм имеет право на жизнь, их использование определяется только целью моделирования и связанным с этой целью выбранным уровнем абстракции при решении проблем» (Карпов, 2008).
| [4] М. Страшкраба (Milan Straskraba; 1931–2000) – чешский математик, эколог, гидробиолог. |
Выше были описаны некоторые более обобщенные (аналитические) подходы к моделированию метапопуляционных процессов (шире – пространственно-распределенных систем). Среди методов моделирования имитационного плана наиболее пригодным для этих целей является индивидуально-ориентированное моделирование (индивидуум-ориентированное или агент-ориентированное; от англ. individual-based modeling [IBM] или agent-based simulation [ABS]) – относительно молодое направление в имитационном моделировании (первые работы в этой области появились 50 лет назад) [5]. Индивидуально-ориентированное моделирование следует рассматривать как логичное развитие ставших классическими методов системной динамики Д. Форрестера [6] (1978), которые основаны на индивидуальном поведении объектов-агентов и оперируют усредненными для группы сходных объектов значениями параметров. Этот подход позволяет учесть влияние фрагментации местообитаний на существование растений и животных. Так, «мозаичный тип размещения оседлых животных возникает в том случае, если пригодные для заселения биотопы распределены в пространстве резко неравномерно. Например, поселения малого суслика в волго-уральской полупустыне приурочены только к пятнам степной растительности, встречающимся среди сплошных песков. Обыкновенный хомяк в полупустыне обитает только в тростниковом поясе озер и на склонах озерных котловин» (Чернова, Былова, 2004, c. 234).
| [5] Фактически индивидуально-ориентированное моделирование стало развиваться еще в конце 1940-х гг. вместе с вычислительными машинами Д. фон Неймана (создание точных копий самих себя), развитием клеточных автоматов С. Улама) и, главное, созданием на этой основе Д. Конвеем в 1970 г. компьютерной игры «Жизнь» («Game of Life» или «Conway Game») – двухмерной клеточно-автоматной модели с двумя состояниями клеток.
Д. Нейман фон (John [János Lajos] von Neumann; 1903–1957) – венгерский, американский математик. С. Улам (Stanisław Marcin Ulam; 1909–1984) – польский, американский математик. Д. Конвей (John Horton Conway; 1937–2020) – британский, американский математик. [6] Д. Форрестер (Jay Wright Forrester; 1918–2016) – американский инженер, системолог. |
Индивидуально‐ориентированное моделирование использует подход, в рамках которого основным объектом (элементом) модели является индивид (агент; для популяции – особь), представляющий собой уникальную, дискретную единицу, у которой есть некоторый набор характеристик, изменяющихся в течение жизненного цикла. Каждый из индивидов взаимодействует с другими индивидами. Модели этого типа строят «снизу вверх», начиная с элементов системы. Модельер определяет только поведение индивидов, а общее поведение системы является результатом совокупной деятельности всех агентов, каждый из которых следует своим собственным правилам взаимодействия со средой и другими индивидами (полное соответствие с определением «экосистемы»). Целью моделирования в этом случае является понимание того, каким образом интегральные (эмерджентные) свойства системы возникают из множества локальных взаимодействий между ее элементами (индивидуумами) (Шеин, Рыжова, 2016, с. 34).
Индивидуально-ориентированная (агентная) модель, как уже отмечалось, представляет реальный мир в виде многих отдельно специфицируемых активных подсистем, называемых агентами (или индивидуумами). Как подчеркивает информатик Ю. Г. Карпов (2008), «каждый из агентов взаимодействует с другими агентами, которые образуют для него внешнюю среду, и в процессе функционирования может изменить как внешнюю среду, так и свое поведение. Обычно в таких системах не существует глобального централизованного управления, агенты функционируют по своим законам асинхронно». Агент-индивид [7] в рамках этих моделей рассматривается как уникальная, дискретная единица, у которой есть некоторый набор характеристик, изменяющихся в течение жизненного цикла. Модели, основанные на данном подходе, строят «снизу вверх», начиная с «частей» системы (индивидов), описывая в итоге всю систему. Целью исследования часто становится понимание того, каким образом свойства системы возникают из взаимодействия между частями (Grimm et al., 1999). IBM – это имитационные модели, построенные для изучения интегральных характеристик систем, состоящих из сходных объектов (например, популяции), как результата множества локальных взаимодействий членов этих систем (особей-индивидуумов). В этом находит свое проявление принцип рекуррентного объяснения (Розенберг, 2013), когда свойства систем данного уровня иерархической организации мира выводятся в виде теорем (объясняются), исходя из постулируемых свойств элементов этой системы (т. е. систем непосредственно нижестоящего уровня иерархии) и связей между ними.
| [7] Общепризнанного определения понятия «агент» не существует (Schieritz, Milling, 2003); однако есть нечто, что объединяет все индивидуально-ориентированные модели: они существенно децентрализованы (Борщёв, 2004; Borshchev, Filippov, 2004). В отличие от моделей «форрестерского типа» (имитация в рамках системной динамики), здесь нет такого места, где централизованно определялось бы поведение (динамика) системы в целом. «Вместо этого аналитик определяет поведение на индивидуальном уровне, а глобальное поведение возникает (emerges) как результат деятельности многих (десятков, сотен, тысяч, миллионов) агентов, каждый из которых следует своим собственным правилам, живет в общей среде и взаимодействует со средой и с другими агентами. Поэтому агентное моделирование называют ещё моделированием снизу вверх» (Борщёв, 2004, с. 42). |
Теоретической основой IBM являются метод Монте-Карло (в более широком плане – эволюционное программирование), три «поведенческие» особенности свойств индивидуумов-агентов [8]:
- объектная ориентированность,
- обучаемость (или их эволюция),
- достаточная простота поведения
и вычисление на каждом шаге моделирования равновесия или псевдоравновесия системы, содержащей в себе множество индивидуумов-агентов. Конечная цель IBM – отследить влияние флуктуаций взаимодействия по определенным правилам индивидуумов-агентов, действующих на микроуровне, на показатели системы в целом на макроуровне.
| [8] «Существует множество определений понятия агента. Общим во всех этих определениях является то, что агент – это некоторая сущность, которая обладает активностью, автономным поведением, может принимать решения в соответствии с некоторым набором правил, может взаимодействовать с окружением и другими агентами, а также может изменяться (эволюционировать). Цель агентных моделей – получить представление об этих глобальных правилах, общем поведении системы, исходя из предположений об индивидуальном, частном поведении её отдельных активных объектов и взаимодействии этих объектов в системе» (Карпов, 2005, с. 291). |
Основными свойствами индивидуумов-агентов являются:
- «интеллектуальность» (обучаемость; это свойство должно быть «умеренным» для того, чтобы индивидуумы-агенты не могли «познать» нечто большее, выходящее за рамки правил игры),
- расположение во времени и пространстве (задается некоторая «среда обитания» (может быть представлена и в виде решетки, как в игре «Жизнь», и в виде гораздо более сложной структуры)),
- наличие жизненной цели (это может быть конкретный результат взаимодействия индивидуумов-агентов в среде обитания (например, равновесие), непрекращающийся процесс эволюции, а иногда – бесконечный цикл без определенного решения).
Считается, что IBM дополняет ставшие уже традиционными имитационные (методы системной динамики) и аналитические методы. Последние позволяют охарактеризовать равновесие системы, а индивидуально-ориентированные модели – исследовать возможность получения такого состояния. В идеале индивидуально ориентированные модели могут помочь идентифицировать критические моменты времени, после наступления которых последствия для системы в целом будут иметь необратимый характер. Сравнение методов системной динамики и IBM (Schieritz, Milling, 2003; Борщёв, 2004; Garifullin et al., 2007) дано в табл. 1.
Таблица 1. Сравнительный анализ методов системной динамики и
индивидуально-ориентированного моделирования
| Критерий | Системная динамика | IBM |
| Основной конструктивный блок моделирования | Петля обратной связи | Индивидуум-агент |
| Единица анализа | Структура | Правило |
| Уровень моделирования | Макро | Микро |
| Перспектива | Сверху – вниз | Снизу – вверх (Борщёв, 2004) |
| Адаптация | Изменение доминирующей структуры | Изменение структуры |
| Время | Непрерывное | Дискретное |
| Математический язык | Интегрально-дифференциальные уравнения | Логика |
| Источник динамики | Уровни | События |
Обсуждение индивидуально‐ориентированных моделей экосистем облегчается опубликованием за последние 30 лет ряда обзоров (DeAngelis, Gross, 1992; Hanski, 1999; DeAngelis, Mooij, 2005; Grimm, Railsback, 2005; Хански, 2010; Roughgarden, 2012; Розенберг, 2013, с. 259–289; DeAngelis, Grimm, 2014; James, 2014; Грабарник и др., 2019 и др.). Модели IBM разрабатываются для решения тех вопросов, где индивидуальная изменчивость, локальные взаимодействия и адаптивное поведение необходимы для получения правильных ответов. Существуют (в свободном доступе) специальные программные библиотеки и платформы моделирования для реализации IBM в виде компьютерных программ – Repast, Swarm, Net Logo, Mason, NEW-TIES, SOARS, ArtiSoc, EcoLab, Cormas, Any Logic и др. Последняя среда – Any Logic – поддерживает агентное и другие виды имитационного моделирования (Борщёв, 2004; Карпов, 2005).
Лесная экосистема оказалась одним из наиболее удобных объектов для индивидуально‐ориентированного моделирования (He et al., 1999; Matejicek et al., 2011; Seidl et al., 2012; Колобов, 2014; Shuman et al., 2014; Kolobov, Frisman, 2016 и др.). Кроме лесных экосистем, IBM используется при моделировании других типов растительности (Mony et al., 2011; Комаров и др., 2015), млекопитающих (Кулаков, Ревуцкая, 2011; Бондарь, 2015), гидроэкологических (ихтиологических) систем (M. Clark, Rose, 1997; J. Clark et al., 2011), ландшафтов (Rebaudo et al., 2013), эволюционных процессов (DeAngelis, Mooij, 2005; Haythorne, Skabar, 2013; Romero-Mujalli et al., 2019) и др.
Таблица 2. Онлайн-ресурсы (программное обеспечение для индивидуально-ориентированного моделирования в экологии) и некоторые модели популяций и экосистем (Розенберг, 2013)
| Название | Адрес | Краткий комментарий |
| Swarm | http://www.santafe.edu/projects/swarm | Пакет программ для многоагентного моделирования сложных систем |
| Echo | http://www.santafe.edu/projects/echo/echo.html | Пакет программ для индивидуально-ориентированного моделирования структур в явно заданном дискретном пространстве, развивающихся по генетическому алгоритму |
| XRaptor | http://www.informatik.uni-mainz.de/~polani/XRaptor/XRaptor.html | Пакет программ для экологического моделирования непрерывных виртуальных многоагентных систем |
| Экосистемы | ||
| ATLSS (Across Trophic Level System Simulation) | http://atlss.org | Имитационная модель обширного заболоченного района в южной Флориде к югу от оз. Окичоби (Okeechobee) и резервации Биг-Сайпрес (Big Cypress), где проживает несколько сот человек индейского племени семинолов |
| Facilitating Mobile Objects within the Context of Simulated Landscape | http://blizzard.gis.uiuc.edu/htmldocs/Entity/paper.html | Модель взаимодействия с растительностью популяций травоядных и плотоядных животных в условиях ландшафта, описанного географической информационной системой (GIS) |
| Evolution and Spatial Structure Interact to Influence Plant-Herbivore Population and Community Dynamics | http://www.eeb.princeton.edu/~gregg/fwproc.htm | Индивидуально-ориентированная модель взаимодействия и коэволюции в системе «растение – животное» |
| Insect/Plant Interactions Program | http://www.ctpm.uq.edu.au/virtualplants/InsectPlant.html | Модели роста отдельных особей растений под воздействием отдельных особей насекомых |
| Модель взаимодействия «ячмень – тля» | http://www.cs.ukc.ac.uk/pubs/1996/42/ | Большая пространственная индивидуально-ориентированная модель ячменного поля, находящегося под воздействием Barley Yellow Dwarf Virus, распространяемого тлей |
| Gecko | http://peaplant.biology.yale.edu:8001/
gecko.html |
Пространственно-распределенная модель для описания динамики экосистемы |
| Популяции
· деревья |
||
| Arborgames | http://margay.sscnet.ucla.edu/~reb/arborweb/arbormain.html | Модель для исследования влияния пожаров на видовое разнообразие в лесах Йелоустона [Yellowstone] |
| SmartForest | http: // www.imlab.uiuc.edu/smartforest | Диалоговая модель для решения проблем лесоводства на уровне индивидуальных деревьев |
| Scaling from Trees to Forests | http://www.sciencemag.org/feature/data/deutschman/index.htm | Стохастическая индивидуально-ориентированная модель пространственно-распределенной динамики роста леса, в которой деревья конкурируют за свет |
| · рыбы | ||
| FPM (Fish Population Model) | http: // www.esd.ornl.gov/iab/iab7-7.htm | Модель популяции малоротого (черного) окуня (Micropterus dolomieu) для оценки воздействия на нее сроков начала рыбацкого сезона |
| Модель миграции лосося | http://rebar.bpa.gov/Environment/AIWP/1997/5500500.html | Модель миграции популяции лосося по данным пассивного радиомаяка |
| NerkaSim | http://www.eos.ubc.ca/salmon/nerkasim/nkaindex.html | Модель миграции популяции лосося по данным, полученным с помощью управляемых моментальных фотографий |
| Individual-Based Trout in Stream Flow Model | http://www.stream.fs.fed.us/streamnt/jan99/jan99a2n.htm | Модель популяции форели в потоке |
| · млекопитающие | ||
| Gorilla Simulation | http://www.cs.ukc.ac.uk/people/staff/ms3/gorillas/simulation/ | Модель популяции гориллы |
| Модель популяции зайца-беляка | http://userzweb.lightspeed.net/~jpthomas/research.html | Пространственная модель динамики популяции американского зайца-беляка (Lepus americanus) |
| MOAB (Model of Animal Behavior) | http://www.usgs.gov/tech-transfer/factsheets/FS-056-97.html | Модель перемещения в пространстве животных в процессе кормодобывания |
| Модель популяции оленя | http://lutra.tamu.edu/dms/dms.htm | Модель-тренажер для отработки навыков управления популяцией оленя (Cervidae) |
| · птицы | ||
| The Weaver Project | http://bamboo.mluri.sari.ac.uk/~mattie/test.html | Модель популяции красной шотландской куропатки в вересковой пустоши Шотландии, направленная на поиск стратегии восстановления ее численности |
| Flocking | http://virtual.dcea.fct.unl.pt/~pedro/papers/birds/paper.html | Модель для изучения реакции организмов на образование групп с учетом и без учета пространственной неоднородности (включает модель стаеобразования птиц) |
| Модель популяции птиц | http://www.cqs.washington.edu/~gordie/gordie.bird.html http://www.pwrc.usgs. gov/research/sis98/bosett1s.htm | Модель популяций белоголового орлана (Haliaeetus leucocephalus) и сапсана (Falco peregrinus) на Нормандских островах и славки (Sylviidae) в районе авиабаза Киртленд [Kirtland] в штате Нью-Мексико недалеко от г. Альбукерке (Albuquerque) |
| · насекомые | ||
| Honey Bee Colonies | http://www.ma.umist.ac.uk/dsumpter/beesim/ | Многоагентная модель поведения роя пчел |
| Manta | http://www-poleia.lip6.fr/~drogoulResearch/Manta/manta.htm | Индивидуально-ориентированная модель поведения колонии муравьев |
| Model of Survival and Social Facilitation in Termites | http://scifunam.ifisicacu.unam.mx/mir/termite.html | Клеточно-автоматная нелинейная модель поведения колонии термитов |
| · морские беспозвоночные | ||
| Ship Fouling | http://turtle.gis.umn.edu/people/yc/foul/foul/ | Модель на языке программирования Java applet для демонстрации взаимодействия и возможностей биологического контроля моллюсков при обрастании корпуса судна |
| Pelagic Tunicate | Модель виртуального мезокосма для исследования условий образования скоплений организмов подтипа Оболочников (Salpa fusiformis) | |
| · бактерии | ||
| BacSim | http://www.eeb.yale.edu/ginger/bacillus/ | Модель для описания роста колонии бактерий; построена на основе модели Gecko |
Для большей убедительности рассмотрим модель ценопопуляции Plantago major L. (подорожника большого).
Онтогенетическая поливариантность определяет специфику динамических процессов не только организменного, но и популяционного уровня и позволяет выявить специфичность воздействий различных факторов на данную ценопопуляцию (Комаров, 2004). Для подтверждения этого тезиса была построена дискретная индивидуально-ориентированная модель Plantago major, которая является пространственно-распределенной (размерности 2), дискретной, пространственно-мобильной, с учетом индивидуальных различий, среднего масштаба (Жукова, Комаров, 1990; Комаров, 2004).
Модель работает следующим образом. На «площадке» размером 300 х 300 см случайным образом (по закону Пуассона) «высевается» 300 растений подорожника, живущих в течение 50–100 дискретных шагов по времени (на каждый вегетационный период приходится три шага по времени). Каждое растение представлено в модели 8 возрастными состояниями, физическим возрастом (в шагах модели), классом плотности и рядом других характеристик. Для имитации эффекта розетки введено понятие «мертвой зоны» (пространство вокруг растения, внутри которого не могут прижиться потомки; данные о вероятности гибели растений или перехода из одного возрастного состояния в другое получены экспериментально (Жукова, Комаров, 1991)). В результате проведенных имитационных экспериментов было показано (Комаров, 2004, с. 97):
- модель вполне адекватно описывает динамику природных ценопопуляций;
- исключение возможности как замедленного, так и ускоренного темпа развития всех растений ценопопуляции приводит:
- к нарушению сроков полного онтогенеза растений,
- к преобладанию «разорванных» возрастных спектров (волны возобновления либо перекрываются очень незначительно, либо совсем не перекрываются),
- к более частому переходу ценопопуляции в критическое состояние (нет плодоносящих растений);
- варьирование интенсивности и периодичности семенного возобновления вызывает существенные изменения размаха колебания плотности и возрастности ценопопуляций (редкое и низкоинтенсивное семенное возобновление приводит ценопопуляцию в критическое состояние, а более частое и интенсивное семенное возобновление повышает ее устойчивость).
Таким образом, тезис о том, что динамическая онтогенетическая поливариантность является одним из главных механизмов динамики растений на популяционном уровне, нашла свое подтверждение.
Рассмотрим еще одну модель, которая позволит нам перекинуть мостик между аналитическими и имитационными (индивидуально-ориентированными) моделями, в частности, это модель системы «хищник – жертва»; см. выше (1). Классическая для экологии система проанализирована с использованием языка Any Logic (Борщёв, 2004). В рассматриваемой модели:
- зайцы и рыси имеют конечную продолжительность жизни, так что они умирают также и от старости, а не только будучи съеденными или от голода;
- зайцы и рыси живут в двумерном пространстве (в терминологии агент-ориентированного моделирования говорят, что агенты «space-aware»);
- плотность зайцев ограничена (например, неким пространственным ресурсом, так что зайцы размножаются, только если вокруг достаточно свободного места);
- рысь может поймать зайца только поблизости от места ее обитания;
- рысь охотится периодически;
- если во время охоты заяц не пойман, рысь перемещается;
- если рысь так и не находит зайца в течение определенного времени, она умирает.
На рис. 4 показано решение классической модели Лотки – Вольтерра с нормированием коэффициентов под средние величины реальной системы «зайцы (Lepus americanus) – рыси (Felis canadensis [Lynx lynx])» в Канадской Арктике, представленные по результатам статистики заготовок пушнины Компанией Гудзонова залива (англ. Hudson's Bay Company) с 1845 по 1935 г., которые успешно перекочевывают из одного учебника экологии в другой. Следует отдать должное Ч. Элтону [9], который в середине 20-х годов прошлого столетия, работая в качестве консультанта Компании, сохранил для науки эти данные и первым ввел их в экологическую литературу.

Рис. 4. Классическая (а) и агент-ориентированная (б)
модель системы «хищник – жертва» (вертикальной чертой отмечены три волны, соответствующие рис. 4а)
Fig. 4. Classical (a) and agent-based (b) model of the "predator-prey" system (three waves corresponding to Fig. 4a are marked with a vertical line)
| [9] Ч. Элтон (Charles Sutherland Elton; 1900–1991) – британский зоолог, эколог, один из основателей популяционной экологии. |
На языке Any Logic «агент-рысь» и «агент-заяц» имеют переменные «Location», где хранится их текущее местоположение (вначале оно случайно). Оно меняется при перемещении агентов и влияет на их поведение. У рысей и у зайцев с определенной частотой появляются рысята и зайчата – это моделируется циклическими «таймерами рождений» – «Births», которые создают новых агентов, причем в случае зайцев это зависит от их локальной плотности. Карта состояний зайца состоит всего из двух состояний: жив «Alive» и мертв «Dead» и двух переходов между ними, соответствующих двум различным причинам смерти: возраст и съедение рысью (последнее моделируется «сообщением», которое рысь напрямую посылает зайцу). У рыси поведение более сложное: она охотится через каждые «Lynx Hunting Period» и, если она не находит зайца (это вероятностно зависит от их локальной плотности), то перемещается (изменяет «Location»), оставаясь в голодном состоянии «Hungry»; в случае, если заяц убит (рысь посылает ему сообщение «я тебя съела! – «I ate you!»), она выходит и тут же вновь входит в состояние «Hungry», что (в соответствии с семантикой карт состояний) вызовет «перезапуск» ее «таймаута голодной смерти».
Результаты имитации по агент-ориентированной модели дают гораздо более «богатый выход», чем аналитическая модель Лотки – Вольтерра или даже «скорректированная» с учетом погодных условий самоорганизующаяся модель системы «зайцы – рыси» (Брусиловский, Розенберг, 1981). Это получается за счет неоднородности размещения особей зайцев и рысей по пространству – в процессе анимации каждого шага моделирования хорошо видны «атаки» рысей, их вымирание там, где съедены все зайцы, и быстрое заполнение зайцами свободного от рысей пространства. Агент-ориентированная модель, как и аналитическая, показывает интерпретируемое колебательное поведение (пики популяции рысей следуют за пиками популяции зайцев). В зависимости от параметров рыси могут полностью вымереть (иногда вместе с зайцами), чего никогда не случается в аналитической модели из-за ее непрерывности (Борщёв, 2004). Колебания стохастичны из-за стохастического характера модели.
Еще одна агент-ориентированная модель системы «хищник – жертва» предложена П. Терна [10] (Terna, 2007). Она включает три взаимодействующих уровня:
- трава (кормовая база для жертвы; растет с постоянной скоростью на «свободных» местах «вокруг» уже существующих особей);
- жертвы (в модели они названы кроликами; численность лимитируется наличием травы, прессом хищника и размножением, которое также осуществляется с постоянной скоростью на «свободных» местах «вокруг» уже существующих особей);
- хищники (в модели они названы лисицами; численность лимитируется наличием кроликов и размножением, которое также осуществляется с постоянной скоростью на «свободных» местах «вокруг» уже существующих особей).
При этом «взаимодействие» (поедание травы кроликами и кроликов лисами) происходит только в том случае, когда особи находятся в «пределах видимости» (параметр модели). Как и для модели А. В. Борщёва (2004), визуализация процесса моделирования осуществляется с помощью анимации на каждом шаге (рис. 5).

Рис. 5. Трава (а), кролики (б) и лисы (в) в модели Терна (фрагмент); темная область – особи (агенты) трех этих групп организмов, светлая область – зона возможного роста травы (а) и «видимости» (б и в)
Fig. 5. Grass (a), rabbits (б) and foxes (в) in Terna's model (fragment); the dark area is the individuals (agents) of these three groups of organisms, the light area is the zone of possible grass growth (a) and "visibility" (б and в)
| [10] П. Терна (Pietro Terna; г. р. 1944) – итальянский математик, экономист, профессор университета в Торино (Италия). |
Заключение
Для моделирования метапопуляционных процессов можно использовать как точечные модели (традиционные популяционные модели) с распределенными параметрами, так и индивидуально‐ориентированные имитационные модели. Второй подход требует больше усилий, более длительных временных рамок и большего количества навыков, чем традиционное моделирование популяций. Есть по крайней мере два условия, выполнение которых позволяет компенсировать кажущиеся более высокие усилия для IBМ, что делает этот подход более эффективным и действенным (Bridle et al., 2010; Stillman et al., 2015).
Во-первых, IBМ создает модели, которые являются более общими и пригодными для повторного использования, чем модели, основанные исключительно на эмпирических параметрах (уход от детерминизма к стохастизму; см. рис. 1). Детерминированный (эмпирический) подход требует, чтобы размер популяции и условия окружающей среды достаточно различались в течение периода исследования, и чтобы они не были сильно скоррелированы друг с другом; для многих видов трудно (или невозможно) измерить необходимые параметры популяционных процессов за достаточно длительный период времени. Напротив, модели IBM, основанные на устоявшейся теории индивидуального уровня, могут быть реализованы, подтверждены и использованы за долю времени, необходимого для разработки эмпирической модели населения (Stillman, Goss-Custard, 2010). Второе условие повышения эффективности проектов этого подхода – высокая отдача, т. к. IBМ обеспечено созданием гибких программных инструментов, что позволяет прийти к моделям, которые являются более гибкими и прогностическими, чем традиционные популяционные модели.
Возможна и третья причина (Hanski, Gaggiotti, 2004; Хански, 2010, с. 306). В классической метапопуляционной теории численность каждой популяции изменяется независимо от численности соседних под действием случайных факторов (демографическая стохастичность). Иными словами, метапопуляция – это «совокупность дискретных локальных популяций вида, обладающих асинхронной динамикой численности и связанных между собой небольшими миграциями; отдельные локальные популяции могут вымирать и замещаться новыми за счет миграции из оставшихся популяций (при этом асинхрония биологической динамики локальных (суб)популяций исключает их одновременное вымирание). Таким образом, метапопуляция способна существовать неизмеримо дольше, чем любая из локальных популяций» (Салменкова, 2018, с. 7). Чем меньше популяция, тем больше шансов, что она исчезнет. Несмотря на то, что популяции уязвимы, сама метапопуляция благодаря постоянным иммиграционным процессам устойчива. Это позволяет совершенствовать моделирование метапопуляционных процессов за счет рассмотрения метасообществ (metacommunity) – сообществ, состоящих из нескольких взаимодействующих метапопуляций, или совокупности локальных сообществ, связанных между собой множественными миграциями слагающих их видов.
Наконец, можно поспекулировать и на таком примере. В некоторых городах (таких как Тольятти, Димитровград, Нижний Новгород и др.) отдельные районы находятся на расстоянии друг от друга (разделены городскими лесами или реками), что позволяет рассматривать их население как городскую метапопуляцию. Более того, в качестве таковых можно рассматривать и крупные городские агломерации (Титов и др., 1996; Любовный, 2011; Крупные городские..., 2015; Экономика российских..., 2020; Е. Антонов и др., 2022). Трудно себе представить, что все районы такой самой большой в митре агломерации, как Чунцин (Китай; население – 52 млн чел. (больше всей Испании; только 4 страны Западной Европы больше по населению), площадь – 83 тыс. км2 (больше всей Австрии)), как-то не изолированы (субпопуляции) и одинаково посещаемы (миграция). Подобный учет «пространственной составляющей» позволит более корректно моделировать структуру и развитие таких территорий.
В качестве примера (рис. 6) продемонстрируем размещение населения г. Тольятти (благо, мы в нем живем и хорошо знаем). Население (2021 г.) – более 690 тыс. чел. (20-й в стране по численности населения и первый среди не областных центров; площадь – 315 км2); три района города (Автозаводской (население 425 тыс. чел., площадь – 89 км2), Центральный (155 тыс. чел.) и Комсомольский (110 тыс. чел.)) разделены лесными массивами (Оценка состояния..., 1995) общей площадью около 8 тыс. га (25 % от всей территории). Это делает поездку из одного района в другой сравнимой с поездкой между городами («гордые» жители Автозаводского района очень редко, если это только не связано с работой, посещают остальные районы, а для некоторых жителей Комсомольского района легче попасть в Москву или Турцию, чем в Автозаводской район). Иными словами, для описания структуры и динамики населения всего г. Тольятти применимы, например, методы индивидуально-ориентированного моделирования.
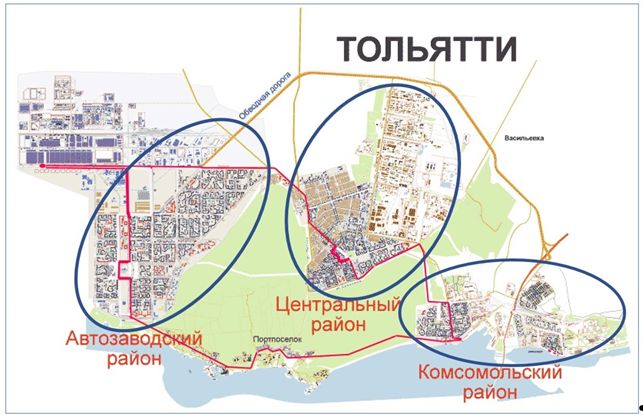
Рис. 6. Размещение населения г. Тольятти (три субпопуляции)
Fig. 6. Population distribution of the city of Togliatti (three subpopulations)
Завершая этот обзор и отдавая себе отчет в том, что некоторые из описанных методов моделирования метапопуляционных процессов будут для экологов относительно сложны и не всегда понятны, приведем забавный случай с Т. фон Карманом [11] – математиком, прославившимся аэродинамическими уравнениями (теория вихрей Кармана). Он был профессором в Ахене (Aachen, Германия), и, поскольку консультировал несколько авиакомпаний, ему была предоставлена возможность бесплатно летать для чтения лекций в Пасадену (Калифорнийский технологический университет, США). Однажды он прибыл на лекцию в Пасадену, начал ее читать, но через некоторое время увидел, «что выражение на лицах не столь осмысленное, как обычно. И тогда он поймал себя на том, что говорит по-немецки. Это его смутило. "Но почему же вы молчите?" – обратился он к слушателям. Студенты не отвечали, наконец один изрек: "Не расстраивайтесь, профессор. Можете говорить по-немецки, можете по-английски, мы поймем не больше"» (Пойя, 1965, с. 48–49). Хочется надеяться, что читатель отнесется к описанным методам с уважением, улыбкой и радостью познания.
| [11] Т. Карман фон (Theodore von Kármán; 1881–1963) – американский математик, инженер, механик венгерского происхождения. |
Библиография
Антонов А. И., Горяйнов А. Г. Большая новейшая энциклопедия рыбалки . М.: ЛитРес, 2010. 660 с.
Антонов Е. В., Куричев Н. К., Трейвиш А. И. Исследования городской системы и агломераций в России // Известия РАН. Сер. географ. 2022. Т. 86, № 3. С. 310–331.
Базыкин А. Д. Нелинейная динамика взаимодействующих популяций . М.; Ижевск: Институт компьютерных технологий, 2003. 368 с.
Бондарь М. Г. Многолетняя динамика и современное состояние популяции лесного северного оленя (Rangifer tarandus valentinae) Алтае-Саянской горной страны // Вестник КрасГАУ. 2015. № 5. С. 40–44.
Борщёв А. В. Практическое агентное моделирование и его место в арсенале аналитика // Exponenta PRO. 2004. № 3-4 (7-8). С. 38–47.
Борщёв А. В. Применение имитационного моделирования в России – состояние на 2007 г. // 3-я Всероссийская научно-практическая конференция по имитационному моделированию ИММОД 2007; Санкт-Петербург, 17–19 октября 2007 г. СПб.: ФГУП ЦНИИ технологии судостроения, 2007. С. 11–16.
Брусиловский П. М., Розенберг Г. С. О возможности построения модели, удовлетворительно описывающей колебания в одной реальной системе хищник-жертва // Динамика эколого-экономических систем. Новосибирск: Наука, 1981. С. 84–91.
Вольтерра В. Математическая теория борьбы за существование . М.: Наука, 1976. 288 с.
Гиляров А. М. Популяционная экология: Учеб. пособие . М.: Изд-во МГУ, 1990. 191 с.
Грабарник П. Я., Шанин В. Н., Чертов О. Г., Припутина И. В., Быховец С. С., Петропавловский Б. С., Фролов П. В., Зубкова Е. В., Шашков М. П., Фролова Г. Г. Моделирование динамики лесных экосистем как инструмент прогнозирования и управления лесами // Лесоведение. 2019. № 6. С. 488–500.
Домбровский Ю. А., Маркман Г. С. Пространственная и временная упорядоченность в экологических и биохимических системах . Ростов н/Д.: Изд-во Ростов. госун-та, 1983. 118 с.
Дохман-Гармиза Г. Социальная жизнь растений . М.: Московский рабочий, 1927. 60 с.
Жариков В. В. Концепция природно-технического каскадного комплекса экосистем Волжских водохранилищ // Экологические проблемы бассейнов крупных рек: Тезисы докладов Международной конференции. Тольятти: ИЭВБ РАН, 1998. С. 15–17.
Жукова Л. А., Комаров А. С. Поливариантность онтогенеза и динамика ценопопуляций растений // Журнал общей биологии. 1990. Т. 51, № 4. С. 450–461.
Жукова Л. А., Комаров А. С. Количественный анализ динамической поливариантности в ценопопуляциях подорожника большого при разной плотности посадки // Научные доклады высшей школы. Биол. науки. 1991. № 8. С. 51–67.
Карпов Ю. Г. Имитационное моделирование систем. Введение в моделирование с AnyLogic 5 . СПб.: БХВ-Петербург, 2005. 400 с.
Карпов Ю. Г. Моделирование агентов – новая парадигма в имитационном моделировании . 2008. URL: https://masters.donntu.ru/2008/fvti/dovzhik/libary/st9.htm.
Колобов А. Н. Моделирование пространственно-временной динамики древесных сообществ: индивидуально-ориентированный подход // Лесоведение. 2014. № 5. С. 72–82.
Комаров А. С. Имитационные модели нелинейной динамики сообществ растений : Дис. ... д-ра биол. наук. Пущино; Тольятти: ИЭВБ РАН, 2004. 389 c.
Комаров А. С., Зубкова Е. В., Фролов П. В. Клеточно-автоматная модель динамики популяций и сообществ кустарничков // Сибирский лесной журн. 2015. № 3. С. 57–69.
Крестин С. В., Розенберг Г. С. Об одном механизме «цветения воды» в водохранилище равнинного типа // Биофизика. 1996. Т. 41. Вып. 3. С. 650–654.
Крестин С. В., Розенберг Г. С. Двухмерная модель «цветения воды» в водохранилище равнинного типа // Известия Самарского НЦ РАН. 2002. Т. 4, № 2. С. 276–279.
Крупные городские агломерации России // Сайт VSEON.com. 2015. URL: http://vseon.com/ analitika/aglomeratsiya/krupnye-gorodskie-aglomeracii-rossii.
Кулаков М. П., Ревуцкая О. Л. Применение метапопуляционного подхода к анализу пространственно-временной динамики промысловых животных (на примере популяций кабана и изюбря) // Региональные проблемы. 2011. Т. 14, № 2. С. 12–20.
Кулаков М. П., Фрисман Е. Я. Кластеризация и химеры в модели пространственно-временной динамики популяций с возрастной структурой // Нелинейная динамика. 2018. Т. 14, № 1. С. 13–31.
Кулаков М. П., Фрисман Е. Я. Модель пространственно-временной динамики популяции с возрастной структурой и дальнодействующими взаимодействиями: синхронизация и кластеризация // Математическая биология и биоинформатика. 2019. Т. 14. Вып. 1. С. 1–18. URL: https://www.matbio.org/2019/Kulakov_14_1.pdf.
Лоу A. M., Кельтон В. Д. Имитационное моделирование . 3-е изд. СПб: Питер; Киев: BHV, 2004. 847 с.
Любовный В. Я. Самарско-Тольяттинская агломерация: история формирования и перспективы развития . М.: Экон-Информ, 2011. 169 с.
Марчук Г. И. Методы вычислительной математики . М.: Наука, 1989. 608 с.
Меншуткин В. В. Искусство моделирования (экология, физиология, эволюция) . Петрозаводск; СПб.: РАН, 2010. 416 с.
Миркин Б. М., Наумова Л. Г. Современное состояние, тенденции развития науки о растительности и новое понимание природы растительного сообщества // Успехи современной биологии. 1994. Т. 114. Вып. 1. С. 5–21.
Миркин Б. М., Наумова Л. Г. Наука о растительности: (история и современное состояние основных концепций) . Уфа: Гилем, 1998. 413 с.
Миркин Б. М., Розенберг Г. С. Анализ мозаичности травянистых растительных сообществ. 2. Ценотический уровень // Биологические науки. 1977. № 2. С. 121–126.
Миркин Б. М., Розенберг Г. С. Фитоценология. Принципы и методы . M.: Нauкa, 1978. 212 p.
Миркин Б. М., Розенберг Г. С., Наумова Л. Г. Словарь понятий и терминов современной фитоценологии . М.: Наука, 1989. 223 с.
Одум Ю. Экология: В 2 т. . М.: Мир, 1986. Т. 1. 328 с.; Т. 2. 376 с.
Оценка состояния и устойчивости лесов зеленой зоны города Тольятти / Отв. ред. Е. Г. Мозолевская, Г. С. Розенберг. Тольятти: ИЭВБ РАН, 1995. 92 с.
Паутова В. Н., Номоконова В. И. Продуктивность фитопланктона Куйбышевского водохранилища . Тольятти: ИЭВБ РАН, 1994. 188 с.
Пойя Д. Мои знакомые математики // Наука и жизнь. 1970. № 6. С. 48–51.
Работнов Т. А. Фитоценология . 2-е изд. М.: Изд-во МГУ, 1983. 296 с.
Реймерс Н. Ф. Природопользование: Словарь-справочник . М.: Мысль, 1990. 637 с.
Ризниченко Г. Ю., Рубин А. Б. Биофизическая динамика продукционных процессов . М.; Ижевск: Институт компьютерных технологий, 2004. 464 с.
Розенберг Г. С. Введение в теоретическую экологию: В 2 т. . Изд. 2-е, испр. и доп. Тольятти: Кассандра, 2013. Т. 1. 565 с.; Т. 2. 445 с.
Розенберг Г. С. Системный подход в глобалистике на примере современных социо-эколого-экономических систем // Век глобализации. 2022. № 4 (44). C. 28–48.
Розенберг Г. С., Мозговой Д. П., Гелашвили Д. Б. Экология. Элементы теоретических конструкций современной экологии (Учебное пособие) . Самара: Самарский НЦ РАН, 1999. 396 с.
Салменкова Е. А. Популяционные системы, метапопуляции, биокомплексность // Успехи современной биологии. 2018. Т. 138, № 1. С. 3–11.
Свирежев Ю. М. Нелинейные волны, диссипативные структуры и катастрофы в экологии . М.: Наука, 1987. 368 с.
Тимохина А. Ф. Зоопланктон как компонент экосистемы Куйбышевского водохранилища . Тольятти: ИЭВБ РАН, 2000. 193 с.
Титов К. А., Любовный В. Я., Хасаев Г. Р. Самарско-Тольяттинская агломерация: современное состояние и пути устойчивого развития . М.: Наука, 1996. 208 с.
Фитопланктон Нижней Волги. Водохранилища и низовье реки . СПб.: Наука, 2003. 232 с.
Форрестер Дж. Мировая динамика . М.: Наука, 1978. 168 с.
Хански И. Ускользающий мир: экологические последствия утраты местообитаний: пер. с англ. . М.: Тов-во науч. изд. КМК, 2010. 340 с.
Чернова Н. М., Былова А. М. Общая экология: Учебник . М.: Дрофа, 2004. 416 с.
Шварц С. С. Внутривидовая изменчивость млекопитающих и методы ее изучения // Зоологический журнал. 1963. Т. 4. Вып. 3. С. 417–433.
Шварц С. С. Эволюционная экология животных и ее задачи // Журнал общей биологии. 1965. Т. 26, № 5. С. 528–537.
Шварц С. С. Популяционная структура вида // Зоологический журнал. 1967. Т. 46. Вып. 10. С. 1456–1469.
Шварц С. С. Экологические механизмы эволюционного процесса // Вестник АН СССР. 1968. № 5. С. 57–66.
Шварц С. С. Эволюционная экология животных . Свердловск: РИСО УФАН СССР, 1969. 200 с.
Шварц С. С. Эволюционная экология // Современные проблемы экологии. (Доклады). М.: Изд-во МГУ, 1973. С. 52–62.
Шеин Е. В., Рыжова И. М. Математическое моделирование в почвоведении: Учебник . М.: ИП Маракушев А. Б., 2016. 377 с.
Шеннон Р. Имитационное моделирование систем – искусство и наука . М.: Мир, 1978. 420 с.
Шитиков В. К., Розенберг Г. С., Зинченко Т. Д. Количественная гидроэкология: методы, критерии, решения: В 2 кн. . М.: Наука, 2005. Кн. 1. 281 с.; Кн. 2. 337 с.
Эдмондсон Т. Практика экологии. Об озере Вашингтон и не только о нем . М.: Мир, 1998. 299 с.
Экономика российских городов и городских агломераций. Вып. 4: Новые подходы к оценке валового городского продукта и его структуры . М.: Фонд «Институт экономики города», 2020. URL: http://www.urbaneconomics.ru/urbaneconomics.
Borshchev A., Filippov A. From system dynamics and discrete event to practical agent based modeling: reasons, techniques, tools // The 22nd International Conference of the System Dynamics Society. Oxford (England): System Dynamics Society, 2004. 22 p. URL: http://www.systemdynamics.org/conferences/2004/SDS_2004/PAPERS/381BORSH.pdf.
Bridle J. R., Polechová J., Kawata M., Butlin R. K. Why is adaptation prevented at ecological margins? New insights from individual-based simulations // Ecol. Letter. 2010. Vol. 13. P. 485–494.
Clark J. R., Daines S. J., Lenton T. M., Watson A. J., Williams H. T. P. Individual-based modelling of adaptation in marine microbial populations using genetically defined physiological parameters // Ecol Modelling. 2011. Vol. 222. P. 3823–3837.
Clark M. E., Rose K. A. Individual-based model of stream-resident rainbow trout and brook char: model description, corroboration, and effects of sympatry and spawning season duration // Ecol. Modelling. 1997. Vol. 94. P. 157–175.
DeAngelis D. L., Grimm V. Individual-based models in ecology after four decades // F1000Prime Reports. 2014. P. 1–6. URL: https://archive.org/details/pubmed-PMC4047944/page/n5/mode/2up.
DeAngelis D. L., Gross L. J. Individual-Based Models and Approaches in Ecology: Populations, Communities and Ecosystems. N. Y.: CRC Press; Boston (MA): Springer US, 1992. 545 p.
DeAngelis D. L., Mooij W. M. Individual-based modelling of ecological and evolutionary processes. 1 // Annu. Rev. Ecol. Evol. Syst. 2005. Vol. 36. P. 147–168.
Garifullin M., Borshchev A., Popkov T. Using Anylogic and Agent-Based Approach to Model Consumer Market. 2007. URL: http://www.xjtek.com/support/download/papers/.
Gause G. F. The Struggle for Existence. Baltimore: Williams & Wilkins Сo., 1934. 163 р.
Grimm V., Railsback S. Individual-Based Modeling and Ecology. Princeton (NJ): Princeton Univ. Press, 2005. 448 р.
Grimm V., Wyszomirski T., Aikman D., Uchmanki J. Individual-based modelling and ecological theory: synthesis of a workshop // Ecol. Modelling. 1999. Vol. 115. P. 275–282.
Hanski I. Metapopulation ecology. Oxford: Oxford Univ. Press, 1999. 313 p.
Hanski I., Gaggiotti O. Ecology, Genetics and Evolution of Metapopulations. London: Elsevier Acad. Press, 2004. 696 p.
Haythorne S., Skabar A. An improved pattern-guided evolution approach for the development of adaptive individual-based ecological models // Ecol. Modelling. 2013. Vol. 252. P. 72–82.
He H. S., Mladenoff D. J., Boeder J. An object-oriented forest landscape model and its representation of tree species // Ecol. Modelling. 1999. Vol. 119, No 1. P. 1–19.
Jackson J. B. C. Bivalves; spatial and size-frequency distributions of two intertidal species // Science. 1968. Vol. 161. P. 479–480.
James J. Methodological individualism in ecology // Philosophy of Sci. 2014. Vol. 81, No 5. P. 770–784.
Kolobov A. N., Frisman E. Ya. Individual-based model of spatio-temporal dynamics of mixed forest stands // Ecol. Complexity. 2016. Vol. 27. P. 29–39.
Levins R. Some demographic and genetic consequences of environmental heterogeneity for biological control // Bull. Entomological Soc. America. 1969. Vol. 15, No 3. P. 237–240.
Matejicek L., Vavrova E., Cudlin P. Spatio-temporal modelling of ground vegetation development in mountain spruce forests // Ecol. Modelling. 2011. Vol. 222, No 14. P. 2584–2592.
Mony C., Garbey M., Smaoui M., Benot M.L. Large scale parameter study of an individual-based model of clonal plant with volunteer computing // Ecol. Modelling. 2011. Vol. 222, No 4. P. 935–946.
Rebaudo F., Le Rouzic A., Dupas S., Silvain J.-F., Harry M., Dangles O. SimAdapt: an individual-based genetic model for simulating landscape management impacts on populations // Methods Ecol. Evol. 2013. V. 4. P. 595–600.
Romero-Mujalli D., Jeltsch F., Tiedemann R. Individual-based modeling of eco-evolutionary dynamics: state of the art and future directions // Reg. Environ. Change. 2019. V 19. P. 1–12.
Roughgarden J. Individual based models in ecology: An evaluation, or how not to ruin a good thing // Philosophy of Science Association Biennial Meeting, San Diego, 2012. Unpublished manuscript, PhilSci Archive. 2012. URL: http://philsci-archive.pitt.edu/9434/1/RoughgardenPSA2012IBMLecture.pdf, https://core.ac.uk/download/pdf/148349671.pdf.
Rozenberg G. S., Krestin S. V. System of analytical models of processes of eutrophication in the reservoir (block approach) // Programme and Abstracts. 3rd International Conference on Reservoir Limnology and Water Quality. Ceske Budejovice (Czech Republic), 1997. Р. 151.
Schieritz N., Milling P. Modeling the forest or modeling the trees – a comparison of system dynamics and agent-based simulation // The 21st International Conference of the System Dynamics Society. N. Y.: System Dynamics Society, 2003. 15 p. URL: http://iswww.bwl.uni-mannheim.de/Forschung/pr/sd03/p-na.pdf.
Seidl R., Rammer W., Scheller R. M., Spies T. A. An individual-based process model to simulate landscape-scale forest ecosystem dynamics // Ecol. Modelling. 2012. Vol. 231. P. 87–100.
Shuman J. K., Shugart H. H., Krankina O. N. Testing individual-based models of forest dynamics: Issues and an example from the boreal forests of Russia // Ecol. Modelling. 2014. Vol. 293. P. 102–110.
Stephens P. A., Sutherland W. J., Freckleton R. P. What is the Allee effect? // Oikos. 1999. Vol. 87, No 1. P. 185–190.
Stillman R. A., Goss-Custard J. D. Individual-based ecology of coastal birds // Biol. Reviews. 2010. Vol. 85. P. 413–434.
Stillman R. A., Railsback S. F., Giske J., Berger U., Grimm V. Making predictions in a changing world: the benefits of individual-based ecology. Bioscience. 2015. Vol. 65. P. 140–150.
Terna P. Agent based artificial experiments in social science with jESOF // J. Social Complexity. 2007. Vol. 3. P. 75–84.
Timofeeff-Ressovsky N. W. Mutations and geographical variations // The New Systematics (Ed. Huxley J.). Oxford: Clarendon Press, 1940. P. 73–136.
Благодарности
Работа выполнена в соответствии с Программой фундаментальных научных исследований государственных академий наук согласно тематическому плану Института экологии Волжского бассейна РАН по теме «Структура, динамика и устойчивое развитие экосистем Волжского бассейна».






 © 2011 - 2025
© 2011 - 2025