Горбач В. В. Опыт оценки абсолютной численности популяции по распределению числа отловов в эксперименте с мечением на примере имаго перламутровок рода Boloria (Insecta, Lepidoptera, Nymphalidae) // Принципы экологии. 2018. № 3. С. 24–33. DOI: 10.15393/j1.art.2018.7763

Выпуск № 3

Оригинальные исследования

pdf-версия статьи

574.34:595.789:57.087.1

Опыт оценки абсолютной численности популяции по распределению числа отловов в эксперименте с мечением на примере имаго перламутровок рода Boloria (Insecta, Lepidoptera, Nymphalidae)

Введение

В основе одного из наиболее распространенных подходов к оценке абсолютной численности популяций животных лежит метод мечения с повторным отловом особей (MRR-техника: mark – release – recapture). К настоящему времени описано множество модификаций постановки MRR-эксперимента для различных таксономических и экологических групп объектов и выработано немало рекомендаций по использованию математических моделей для аппроксимации результатов исследований. Из руководств на русском языке наиболее популярным среди зоологов остается сводка Г. Коли (1979), из англоязычных изданий – монографии Ч. Кребса (Krebs, 1999), Т. Саусвуда и П. Хендерсона (Southwood, Henderson, 2000). Общий принцип всех предлагаемых алгоритмов состоит в том, чтобы по доле меченых особей в отловах определить число особей, которые не были отловлены ни разу, непременным требованием к выборке является случайность отлова любой особи.

Популяции бабочек обычно изучают методом Джолли – Себера, использующем в качестве математической основы стохастическую модель. Пожалуй, это наиболее информативный подход, который по серии многократно повторяемых отловов позволяет оценить целый ряд скрытых демографических переменных, в частности абсолютную численность, численность для каждой даты исследования, скорость роста и т. д. Вместе с тем этот метод обладает рядом особенностей, которые снижают его эффективность. Практика применения указывает на чувствительность используемой модели к малым выборкам, периодичности и пропорциональности отловов (Горбач, 2013). В первом случае бывает невозможно провести расчеты из-за пропуска повторных отловов меченых особей в малочисленных популяциях, другие затруднения обычно возникают из-за неблагоприятных для лета бабочек погодных условий, которые нередко увеличивают временные интервалы между запланированными этапами (датами) мечения или вынуждают досрочно завершить очередной этап, не дав отловить достаточное число особей. В случаях подобных сбоев в ходе эксперимента остается возможность оценить абсолютную численность по одному из известных законов распределения частот. Правильная стратегия в этом случае состоит не в том, чтобы использовать для расчетов какую-либо модель, бездумно принимая на веру лежащую в ее основе гипотезу, а в том, чтобы из имеющихся вариантов выбрать наилучший по адекватности экспериментальным данным (Коли, 1979).

Цель настоящей работы состоит в сравнении оценок абсолютной численности и в обобщении опыта использования дискретных распределений для описания частот отловов особей в экспериментах с перламутровками рода Boloria. В качестве теоретической платформы мы выбрали две модели – распределение Пуассона и геометрическое распределение, которое в случае с бабочками лучше других описывает результаты экспериментов.

Материалы

Объектами изучения стали два вида бабочек-перламутровок рода Boloria – B. freija (Thunberg, 1791) и B. aquilonaris (Stichel, 1908). Это типичные ледниковые реликты лесной зоны, населяющие в Карелии сфагновые болота. Поскольку болотные массивы представляют собой местообитания островного типа, то и популяции изучаемых видов распадаются на пространственно разобщенные группировки, приуроченные к отдельным выделам. Исследования проводили в заповеднике «Кивач» на сопредельных болотах Близкое и Осоковое, ранее рассматриваемых нами как единый массив (Горбач, 1998, 2011). Данные для анализа выбирали, учитывая дифференциацию объектов по численности: B. aquilonaris является обычным болотным видом, тогда как B. freija – одним из малочисленных. То же касается и рассматриваемых сезонов: 1995 г. стал самым удачным для B. aquilonaris за последние десятилетия, численность же B. freija была настолько низкой, что не имело смысла начинать эксперимент, в сезоне 1996 г. она достигла локального максимума, в 2016 г. соответствовала обычному для этого вида уровню. Общий объем выборок составляет 3889 меченых бабочек (табл. 1 и 2).

 

Таблица 1. Распределение частот отлова перламутровок B. freija и оценки абсолютной численности вида на исследуемой территории

Table 1. Distribution of the Freija fritillary captures and the estimates of the absolute number of the butterflies in the study area

k	1996			2016
	самцы	самки	имаго	самцы	самки	имаго
1	61	42	103	19	18	37
2	37	29	66	17	11	28
3	10	3	13	7	3	10
4	1		1	1	1	2
5				1		1
Распределение Пуассона
Np, экз.	178	131	307	60	51	110
lim, экз.	159÷206	114÷157	276÷338	54÷70	43÷69	100÷125
χ2	2.638	7.123	8.445	1.424	0.244	1.081
p	0.450	0.028	0.037	0.840	0.970	0.897
Геометрическое распределение
Ng, экз.	305	228	524	97	86	182
lim, экз.	266÷365	194÷282	469÷599	84÷118	69÷121	159÷214
χ2	10.197	14.307	23.625	6.125	1.975	7.477
p	0.017	<0.001	<0.001	0.190	0.578	0.113
Стохастическая модель динамики численности Джолли – Себера
Njs, экз.	216	114	314	119	102	198
SE, экз.	121	61	141	64	81	93

Примечание. k – частотные классы эмпирического распределения (число отловов особи), Ng, Np, Njs – абсолютная численность, lim – доверительный интервал, SE – стандартная ошибка, χ² и p – оценка и значимость отличий эмпирического и теоретического распределений (критерий Пирсона), жирным шрифтом указаны значимые различия p<∝ = 0.05.

Note. k are classes of the empirical frequencies (number of captures of the individual); Ng, Np, Njs - absolute numbers by Poison, geometric and Jolly – Seber models, accordingly; lim – confidence interval; SE – standard error; χ² and p – estimatе and significance of differences between empirical and theoretical distributions (Pearson's criterion), significant differences (p<∝ = 0.05) are indicated in bold.

 

Таблица 2. Распределение частот отлова перламутровок B. aquilonaris и оценки абсолютной численности вида на исследуемой территории

Table 2. Distribution of the Cranberry fritillary captures and the estimates of the absolute number of the butterflies in the study area

k	1995			1996
	самцы	самки	имаго	самцы	самки	имаго
1	941	985	1926	690	514	1237
2	109	132	241	106	82	188
3	12	9	21	8	5	13
4		2	2
Распределение Пуассона
Np, экз.	4963	4847	9789	3198	2374	5813
lim, экз.	4340÷5847	4285÷5622	8919÷10892	2795÷3747	2054÷2849	5239÷6538
χ2	0.723	2.342	0.328	0.898	1.653	2.146
p	0.697	0.504	0.954	0.638	0.199	0.342
Геометрическое распределение
Ng, экз.	9534	9277	18778	6096	4521	11094
lim, экз.	8285÷11305	8152÷10832	17031÷20990	5278÷7196	3879÷5474	9942÷12548
χ2	0.256	3.315	2.784	4.765	5.409	9.418
p	0.880	0.346	0.426	0.092	0.067	0.009
Стохастическая модель динамики численности Джолли – Себера
Njs, экз.	3762	3420	7203	2041	1590	3761
SE, экз.	1643	1344	2106	1028	783	1442

Примечание. Обозначения см. в табл. 1.

For notations see Table 1.

Методы

Методология получения выборок подробно описана ранее (Горбач, 2013), она стандартна для подхода Джолли – Себера и полностью соответствует требованиям MRR-эксперимента. Общая задача при оценке абсолютной численности состояла в том, чтобы, зная частоту повторных отловов меченых особей (k = 1, 2, 3, 4, …), найти частоту нулевого класса (k = 0), т. е. определить число особей, которые в ходе эксперимента не попались ни разу. Размер этого класса, а следовательно, и величина искомой переменной (суммы всех частот) зависит от характера распределения.

Распределение Пуассона предполагает постоянную вероятность отлова особей, которая возможна только в «закрытой» популяции при очень низкой, в идеале – нулевой смертности за время эксперимента. Распределение частот представляет собой аппроксимацию биномиального распределения для случаев, когда p<<q (Коросов, 2007), где p – вероятность найти объект нужного качества, в нашем случае – отловить меченую особь, q  – вероятность не найти такой объект, 0 < p ≤ 1 и q = 1 − p. Случайная величина принимает при этом целочисленные значения с вероятностью P_{k =} e^−λ·λ^k/k!, где λ – параметр распределения, k! – факториал числа k, e – основание натурального логарифма. Абсолютная численность рассчитывается по формуле Np = s/µ, где s – общее число отловов, µ – средняя арифметическая распределения с нулевым классом, которая задается равенством M = µ/(1 − e^−µ). Нахождение значения переменной µ составляет определенную сложность, поскольку данное уравнение имеет прямое решение лишь в случаях, когда средняя арифметическая усеченного (эмпирического) распределения M > 2. Тогда используют интерполяционные многочлены Лагранжа, в иных случаях искомое значение подбирают методом проб и ошибок (Коли, 1979). Проще эта задача решается средствами оптимизации, встроенными в компьютерные программы, например с помощью пакета «Поиск решения» в среде MS Excel или функции optimize в среде R.

Геометрическое распределение используют для описания процессов, в которых вероятность совершения тех или иных событий не постоянна (Коли, 1979). Считают, что эта модель будет адекватной экспериментальным данным при неравной предрасположенности особей к попаданию в ловушки. Геометрическое распределение является предельным случаем отрицательного биномиального распределения с функцией вероятности P_k = p·q^k. Абсолютная численность рассчитывается как Ng = n·(s − n)/(s − 1), где n – число меченых особей.

Погрешности оценок определяли простым непараметрическим бутстрепом с числом итераций B = 5000 (Шитиков, 2012; Шитиков, Розенберг, 2013). Построив вариационный ряд бутстрепированных значений средней, методом процентилей находили границы ее доверительных интервалов (рис. 1). Пределы изменчивости Np и Ng оценивали по этим экстремумам, приняв s = n·M_lim, где M_lim – минимальное или максимальное значение бутстрепированной средней. Адекватность моделей исходным данным определяли по критерию Пирсона (χ²), сравнивая эмпирические частоты с теоретическими распределениями. Частоты соответствующих теоретических распределений (A_k) вычисляли по общей формуле А_k = N·P_k, где N –  абсолютная численность. Вклад отличий нулевых классов в значение критерия принимали равным нулю, допустив, что число непойманных особей a₀ действительно соответствует рассчитанному значению A₀. Параметры распределений определены как λ = M, p = 1−(s − n)/(s − 1). Использован алгоритм расчетов на языке R (см. скрипт). Число частотных классов теоретического распределения приравнено к числу классов эмпирической выборки, остатки их «хвостов» слиты с частотой A_k последнего класса. При расчете числа степеней свободы учитывали наличие нулевых классов. Оценка абсолютной численности методом Джолли-Себера выполнена в соответствии с ранее опубликованной методикой (Горбач, 2013), в том числе была реализована процедура оптимизации путем подгонки модельных параметров под биологически разумные значения.

 

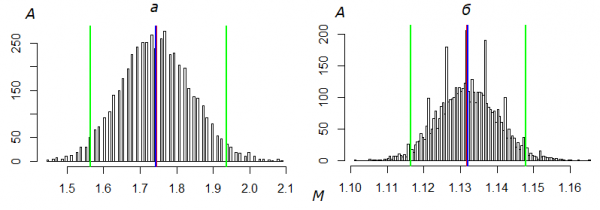
 Рис. 1. Распределение значений средней арифметической числа отловов M, полученных бутстреп-методом для имаго B. freija 2016 г. (а) и B. aqulonaris 1995 г. (б). А  – число выборок (ΣA = B = 5000), красной линией указано значение M исходной выборки, синей – значение M, скорректированное бутстрепом, зелеными – границы доверительного интервала M_min÷M_max

Fig. 1. Distribution of the arithmetic mean value (M) of capture numbers obtained by the bootstrap method for all Freija fritillaries in 2016 (а) and all Cranberry fritillaries in 1995 (б). A is the number of samples (ΣA = B = 5000), the red line indicates the M value of the original sample, the blue line is the M corrected by bootstrap, the green lines are the confidence interval M_min÷M_max

Результаты

Результаты оценки абсолютной численности и последующего анализа распределений частот отловов бабочек в MRR-эксперименте позволили прийти к следующим заключениям: 1) наиболее высокие значения численности дает геометрическая модель, они в полтора-два раза выше Пуассоновых оценок; 2) значения, полученные методом Пуассона, лучше сходятся с модельными оценками Джолли – Себера; 3) распределение Пуассона более адекватно экспериментальным данным. Вместе с тем имеется и несколько отклонений от общих трендов. Так, оценки абсолютной численности, сделанные методом Джолли – Себера по выборкам 2016 г., более сходны с геометрическими оценками (см. табл. 1); отловы самцов B. aquilonaris в 1995 г. геометрическая модель аппроксимирует лучше, чем распределение Пуассона (см. табл. 2).

Общая закономерность в распределении эмпирических частот состоит в недостатке особей, отловленных один раз, и избытке особей, отловленных два раза, по сравнению с теоретическими предсказаниями (рис. 2). Предельный вариант наблюдали у самок B. freija в 1996 г.: отмеченная непропорциональность привела к существенным расхождениям с теоретическими частотами и значимо сказалась на распределении обобщенных частот для всех особей вида в этот сезон. Лишь у упомянутых выше самцов B. aquilonaris эмпирические частоты a₁ = 941, a₂ = 109 и a₃ = 12 смогли попасть в коридор из предсказанных частот Ap÷Ag: 931÷944, 113÷105 и 10÷13.

 

Рис. 2. Частота отловов особей для выборок имаго B. freija 1996 (а) и 2016 г (б). k – число отловов особи (частотные классы), 1 – эмпирические частоты а, 2 – частоты геометрического распределения Ag, 3 –  частоты распределения Пуассона Ap

Fig. 2. The frequencies of captures for all Freija fritillaries in 1996 (а) and 2016 (б). k – the capture number of the specimens (classes of  frequencies), 1 –  empirical frequencies a, 2 –  frequencies of the geometric distribution Ag, 3 – the Poisson’s frequencies Ap

Обсуждение

Стохастическая модель динамики численности Джолли – Себера предсказывает весьма высокий уровень элиминации изученных группировок бабочек за счет гибели и эмиграции особей (Горбач, 2013). Следовательно, требование равной вероятности отловов нарушается, означая, что оценки абсолютной численности, рассчитанные методом Пуассона, не могут быть вполне адекватными и геометрическая модель, допускающая непостоянство вероятности, должна описывать полученные выборки лучше. Между тем результаты сравнения распределений расходятся с этим предположением. Сходство оценок по модели Джолли – Себера, предусматривающей неустойчивость хода демографических процессов, и модели Пуассона свидетельствует о вполне хорошем описательном потенциале последней, указывая на ее вполне приемлемую толерантность к нарушениям равновероятности отловов в ходе эксперимента. Отдавая предпочтение Пуассоновым оценкам, следует подчеркнуть, что здесь речь идет о пространственно обособленных группировках с естественным образом ограниченными входящими и выходящими потоками особей. Соответствие частот распределению Пуассона помимо прочего может служить своего рода индикатором «закрытости» подобных популяционных систем.

К оценкам на основе геометрической модели следует относиться осторожно, как к неоправданно высоким, особенно в случаях больших выборок. С ростом населения снижается вероятность повторных отловов, чем меньше средняя, тем больше прирост нулевого класса и выше оценка численности. Например, если судить по рассчитанной численности B. aquilonaris (см. табл. 2), то получается, что в 1995 г. средняя плотность населения в скоплениях должна составлять около 500 имаго за сезон на учетную площадку 50 × 50 м (Горбач, 2011), но общее число отловленных на этих площадках особей было существенно меньше: оно не превышало 300 при среднем показателе в 50 экз. Дрейф эмпирических частот в сторону геометрического распределения можно трактовать как проявление разного рода демографических возмущений, в частности роста миграционных потоков. Однако в упомянутом выше случае с самцами B. aquilonaris причина была иная, связанная с условиями получения выборки. Дело в том, что неординарное поведение этого вида позволяло продолжать эксперимент при ухудшении погодных условий, когда бабочки переставали летать, – они оставались на соцветиях сабельника, поэтому, обходя скопления этого растения, можно было собирать, метить и возвращать их обратно. При этом существенно уменьшалась доля самцов, многие из которых, в отличие от самок, скрывались в нижнем ярусе растительности, становясь недоступными. Дней с неустойчивой или пасмурной погодой в сезоне 1995 г. было больше половины, поэтому указанная особенность повлияла на общую выборку, и соответствие геометрическому распределению следует рассматривать здесь как следствие изменчивости вероятности отлова самцов в различных условиях.

Ответ на вопрос, почему значения абсолютной численности B. freija в 2016 г., рассчитанные методом Джолли – Себера, сильно отклоняются от Пуассоновых оценок, заключен в нестабильности стохастической модели, прилагаемой к малым выборкам. Участие случайных событий в формировании вариант существенно возрастает, усиливая диспропорции в распределении числа отловов. В результате модельные параметры, используемые для расчета переменных, принимают невозможные с биологической точки зрения значения. Несоответствие их реальности давало заведомо заниженные итоговые оценки, вплоть до того, что рассчитанная абсолютная численность была меньше числа меченых особей. Введение в модель биологически разумных ограничений сделало эти параметры более адекватными, но при этом значения численности стали неоправданно высокими. Понять справедливость этого заключения можно, сравнив равноценные по объему выборки B. freija, полученные для самок в 1996 г. и всех имаго в 2016 г. (см. табл. 1). Во втором случае метод Джолли – Себера дал значение абсолютной численности в 1.7 раза больше. Если же сопоставить обобщенные выборки этого вида, а в том и другом сезоне удавалось отлавливать почти всех замеченных бабочек, то видно, что в 2016 г. обилие было по меньшей мере в два раза ниже, чем в 1996 г. Таким образом, остается констатировать, что и здесь Пуассонова модель более реалистично отражает наблюдаемую действительность.

Отмеченная диспропорция между частотами отловов в выборках и их предсказанными вероятностями (см. рис. 2) говорит в пользу «закрытости» исследованных группировок. Обычно уменьшение числа встреч немеченых особей на фоне роста повторных отловов наблюдается при довольно стабильном составе населения, когда особи подолгу остаются на тех участках, где были помечены, а прирост за счет выхода свежих бабочек из куколок и иммиграции несущественен. В качестве иллюстрации можно предложить выборку B. freija. В сезоне 1996 г. плотность населения этой перламутровки была сравнительно высокой, но тем не менее удавалось отлавливать всех встреченных бабочек. В результате число впервые отловленных особей с каждым посещением местообитания уменьшалось, а встречаемость меченых росла. У самок оседлость проявилась в большей мере, поскольку они, по сравнению с самцами, не так активны поначалу и начинают расселяться, лишь отложив значительную часть яиц в месте своего отрождения. При росте населения, как в случае с B. aquilonaris, возможность отлова каждой замеченной бабочки падает, и, вследствие того, что многие из них остаются немечеными, влияние оседлости на частоту отловов минимизируется. При уменьшении объема выборок, подобно B. freija в 2016 г., перестает работать закон больших чисел, и распределение частот оказывается сильно зависимым от случайности каждой встречи.

Заключение

Частоту отловов бабочек в MRR-эксперименте при изучении пространственно обособленных группировок лучше всего описывает распределение Пуассона. Оценки абсолютной численности, рассчитанные на основе этой модели, представляются наиболее адекватными: в целом они довольно хорошо согласуются со значениями, полученными методом Джолли – Себера. В случае малых выборок аппроксимация экспериментальных данных распределением Пуассона, по-видимому, остается единственно возможным способом получения адекватных оценок численности населения. Смещение эмпирических частот в сторону геометрического распределения может быть индикатором динамичности демографических процессов, – рост элиминации неизбежно уменьшает долю повторных отловов, а активное пополнение популяции ведет к увеличению доли впервые отловленных особей. Рассматривая соответствие распределению Пуассона в качестве меры обособленности группировки, нужно понимать, что локальная оседлость особей может менять характер эмпирического распределения, увеличивая частоту повторных отловов, так, что отличия от теоретического распределения становятся значимыми. Расхождение с Пуассоновой моделью в таком случае будет аргументом в пользу большей «закрытости» изучаемой популяционной системы.

Библиография