Введение
Одной из ключевых задач при изучении динамики популяций является определение абсолютной численности особей для известных временных интервалов. Методы ее оценки применительно к булавоусым чешуекрылым были предложены уже в самых первых работах, посвященных экологии популяций этой группы насекомых (Ford, Ford, 1930; Dowdeswell et al., 1940, 1949). Однако более востребованным оказался подход, в основу которого положена стохастическая модель динамики численности (Jolly, 1965; Seber, 1965). Этот метод, известный как метод Джолли – Себера, позволяет по данным многократных отловов особей рассчитывать не только численность, но и другие демографические параметры. В настоящее время для вычислений обычно используют специальные компьютерные программы, наиболее популярными из которых являются JOLLY (Pollock et al., 1990), MARK (White et al., 1999) и POPAN (Arnason, Schwartz, 1999). Возможен и иной вариант расчетов – в среде MS Excel. Формат электронной таблицы позволяет лучше понять суть производимых операций для вычисления основных переменных, открывая путь к осмысленному применению готовых программных продуктов.
Сложность изучения демографических процессов, происходящих в популяциях насекомых, обусловлена их скрытным образом жизни. В тех случаях, когда особи редко попадаются на глаза и не идут ни в какие ловушки, вряд ли вообще возможно получить сколько-нибудь репрезентативные выборки. Дневные бабочки являются одной из немногих групп, к которым применимы подходы, успешно апробированные на позвоночных животных, в том числе и метод мечения с повторными отловами (Коли, 1979). Работы, посвященные популяциям чешуекрылых, появились еще в первой половине прошлого века в Великобритании, но признанным центром их изучения на следующие десятилетия стала школа, основанная Паулем Эрлихом в Стэндфордском университете (Ehrlich, Davidson, 1960; Ehrlich, 1961; Ehrlich, Raven, 1969; Ehrlich, Hanski, 2004 и др.). С тех пор бабочки являются одним из излюбленных объектов популяционных исследований (Harding, Green, 1991; Settele et al., 2009). Их выбирают в качестве моделей по нескольким причинам. Во-первых, взрослые особи ведут открытый образ жизни, следовательно, за ними легко наблюдать и при необходимости отлавливать. Гусеницы некоторых видов живут на кормовых растениях группами, которые хорошо заметны и также доступны для изучения. Во-вторых, не имея территориального поведения, имаго свободно перемешиваются, обеспечивая случайность их поимки. Это особенно важно для адекватной оценки численности при использовании методов мечения с повторными отловами. В-третьих, многие из видов бабочек приурочены к обособленным местообитаниям, имеющим относительно небольшие размеры и ясно выраженные границы. Появляется возможность охватить исследованием всю населенную территорию и изучать именно популяции или естественным образом сложившиеся внутрипопуляционные группировки особей, а не популяционные явления на некотором участке непрерывного ареала. И, наконец, в-четвертых: бабочки довольно многочисленны, что позволяет в короткие сроки получать достаточные для полноценного анализа выборки. Популяционные исследования, в качестве модельных объектов в которых выступали бы чешуекрылые, в нашей стране только начинаются. И это несмотря на тот факт, что дневные бабочки являются одной из наиболее многочисленных групп насекомых в Красных книгах различного уровня. Призывы к всестороннему изучению охраняемых видов реализуются в основном лишь посредством получения более точной информации об их распространении и особенностях биологии на различных участках ареала. Первые результаты изучения пространственной структуры и динамики популяций ряда карельских видов опубликованы ( Горбач, 1998, 2011; Горбач, Кабанен, 2009; Горбач и др., 2010).
Целью настоящей работы является обобщение опыта, полученного при использовании метода Джолли – Себера, для оценки численности популяций булавоусых чешуекрылых на стадии имаго. Подробно рассмотрены два ключевых аспекта предлагаемого подхода: 1) методика мечения и 2) этапы вычисления основных демографических параметров, реализованные в среде MS Excel.
Материалы
Нашими объектами в разное время были пять видов булавоусых чешуекрылых. Перламутровок Boloria aquilonaris (Stich.), B. eunomia (Esp.) и B. freija (Bckl.) изучали на сфагновом болоте Близкое в заповеднике «Кивач» в 1995–1996 годах (Горбач, 1998; 2011). Тогда же, на шоссейной дороге Водопад Кивач – Сопоха метили ленточников Limenitis populi (L.) (Горбач и др., 2010). Популяцию парусника Parnassius mnemosyne (L.) исследовали на Большом Клименецком острове Онежского озера в 2003–2006 годах (Горбач, Кабанен, 2009). В общей сложности было помечено более 7 тысяч бабочек. Число повторных отловов составило около 2 тысяч.
Методы
Методы полевых исследований. Материал собирали в течение всего периода лета видов, используя метод мечения с повторными отловами. Исследуемые местообитания удавалось посетить за это время от 8 до 17 раз. Передвигаясь по заранее намеченному маршруту, производили отловы с помощью энтомологического сачка. Каждую бабочку регистрировали, впервые пойманных метили и тут же отпускали. В качестве меток использовали арабские цифры (рис. 1), которые наносили ручкой-маркером (PILOT–ID) на нижнюю поверхность левого заднего крыла. Такое расположение не позволяет отличить меченые экземпляры среди летающих бабочек, и идентифицировать особь можно только после её поимки. Следовательно, основополагающий принцип метода – случайность отлова меченых и немеченых особей – не нарушается. Этот аспект приобретает особую значимость при высокой численности популяции, когда невозможно отловить всех замеченных бабочек.

Рис. 1. Меченые особи парусника Parnassius mnemosyne – свежая и облетанная
Fig. 1. Marked clouded Apollo butterflies, there are specimens with fresh and heavily damaged wings
Метки на крыльях сохраняются до конца жизни и могут быть утрачены лишь в случае сильного повреждения крыла, как это, например, происходило с ленточниками, сбитыми автотранспортом (Горбач и др., 2010). Более мелких бабочек и бабочек с темными крыльями удобнее метить посредством кодов, нанося на испод крыльев черточки и/или точки. Одна из систем кодирования представлена на рис. 2. Использование хорошо заметных в полете меток недопустимо, поскольку ведет к субъективизму при отлове особей, становясь причиной грубых ошибок в оценках демографических параметров. В классических работах (Brussard, Ehrlich, 1970 и др.) бабочек метили подобным образом лишь для того, чтобы, отслеживая траекторию движения, не путать их с другими особями. Нанесение меток на верхнюю поверхность крыла также нецелесообразно, поскольку возрастает риск травмирования бабочки.

Рис. 2. Система меток 1-2-4-7 (по Watt et al., 1977). Расположение черточек кодирует порядковый номер особи, числа 3, 5, 6, 8 и 9 получают сложением имеющихся
Fig. 2. System of numbering 1-2-4-7 (from Watt et al., 1977). Disposition of dashes encodes the individual number of a butterfly, numbers 3, 5, 6, 8 and 9 are the sum of the basic elements
Манипуляции, производимые во время мечения, согласно данным Галла (Gall, 1984), не влияют существенным образом на выживаемость бабочек, но вызывает временное снижение их двигательной активности. Обычно этот эффект проявляется в течение нескольких часов, поэтому интервал между отловами не должен быть меньше одних суток. В противном случае снижение активности меченых особей может приводить к искажению оценки численности популяции. Действительно, двигательная активность бабочек снижается, но, по нашим наблюдениям, на более короткое время. Чем крупнее вид, тем легче его особи переносят производимые манипуляции. Опыт показывает, что оптимальная периодичность посещения исследуемых местообитаний составляет 2–3 дня. Другим негативным фактором, влияющим на оценку численности при применении данного метода, может стать уменьшение вероятности повторного отлова меченых бабочек. Было замечено (Singer, Wedlake, 1981), что особей, меченных без отлова (медленное приближение и нанесение метки), вылавливали в несколько раз чаще, чем тех, которых предварительно отлавливали. Причиной снижения вероятности отлова в этом случае может быть более высокая смертность среди бабочек, которых отлавливали (например, в результате травмирования). Предположение о закреплении специфических поведенческих реакций кажется сомнительным, поскольку предполагает наличие у насекомых более сложных форм нервной деятельности, чем нам известно. В любом случае вероятность повторного отлова зависит от подвижности особей, т. е. от возможности для исследователя поймать каждую из встреченных бабочек. При невысокой плотности населения нам удавалось отлавливать почти всех замеченных особей, в том числе и хорошо летающих ленточников.
Наиболее серьезные ограничения на проводимые работы накладывали погодные условия. Метить бабочек при температуре менее 15 °С или сплошной облачности не имеет смысла. В таких условиях падает двигательная активность имаго, они забиваются в траву и становятся незаметными. Только в случае с перламутровкой B. aquilonaris плохая погода не мешала работе. Дело в том, что бабочки в состоянии покоя оставались на соцветиях сабельника – основного кормового растения имаго на исследуемом болоте. Эта особенность дала возможность, планомерно обходя скопления растений, собирать особей с цветков, метить их и возвращать назад. В результате удавалось выдерживать строгие двухдневные интервалы между посещениями местообитания (Горбач, 1998). В других случаях график работ приходилось корректировать: из-за неблагоприятных погодных условий перерывы порой увеличивались до недели и более.
Анализ данных. Демографические параметры оценивали методом Джолли – Себера (Jolly, 1965). Данный подход позволяет определить абсолютную численность для каждой, кроме первой (i = 1) и последней (i = l), даты исследования (i = 2, 3, … l – 1), а также процессы роста и убыли популяции за время между отловами. Для этого необходимо иметь следующие данные о числе меченых особей и повторных отловах:
ni – число отловленных особей в момент времени i;
si – число выпущенных особей;
mi – число особей в выборке ni, помеченных до i-го отлова;
Zi – число особей, помеченных до i-го отлова, не попавшихся при i-м отлове, но отловленных позже;
Ri – общее число особей из si, попавшихся при повторных отловах.
Исходные массивы данных представляли собой матрицы в среде MS Excel (рис. 3). Повторные отловы одной и той же особи в течение дня не учитывали. Численность для каждой даты рассчитывали по формуле:
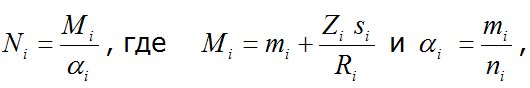
Ni – оценка численности особей в момент времени i;
Mi – общее число особей, помеченных в популяции до i-го отлова;
αi – доля меченых особей, попавшихся при i-м отлове.
Стандартная ошибка оценки численности равна
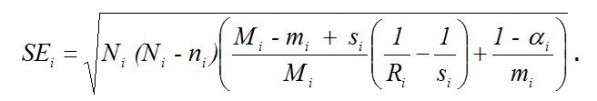
Коэффициент убывания численности (элиминации)
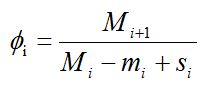
показывает долю особей среди непогибших и не эмигрировавших с исследуемой территории к моменту времени i + 1. Тогда число особей, появившихся из куколок и прибывших на исследуемую территорию за то же время, будет составлять
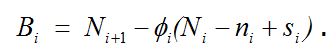
Для øi и Bi, так же как и для Ni, могут быть рассчитаны стандартные ошибки (Jolly, 1965), но на практике эти показатели используют редко.
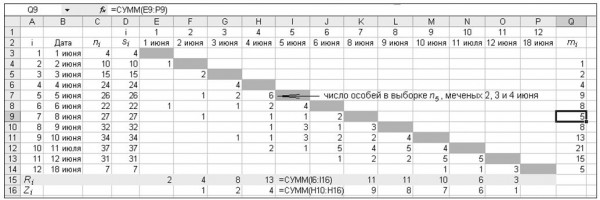
Рис. 3. Результаты отловов имаго перламутровки Boloria freija на болоте Близкое (заповедник «Кивач») в 1996 году. Обозначения переменных даны в тексте
Fig. 3. Results of mark-release-recapture of adult fritillaries Boloria freija on mires Blizkoe (Kivach Nature Reserve) in 1996. ni is the number of individuals captured in a day i; si is the number realized after marking on day i; mi is the number of individuals in the sample of ni marked before day i; Zi – is the total number marked before day i which are not caught on day i, but are caught subsequently; Ri is the total number of the s i individuals that are caught subsequently
Переменные вычисляли для всех особей и, где было возможно, для самцов и самок по отдельности (рис. 4). В случаях, когда из-за недостатка данных расчет по формулам для какого-либо из полов был невозможен, численность определяли исходя из равенства: Ni= Nmi + Nfi, где префиксами m и f обозначены самцы и самки соответственно. Если же пропуски исходных вариант не позволяли определить ни Nmi, ни Nfi, то рассчитанную величину Ni делили согласно соотношению между nmi и nfi. Численность для первого (N1) и последнего (Nl) дня эксперимента принимали равными n1 и nl соответственно. Общую численность популяции определяли согласно выражению Nобщ = N2 + Σ Bi (Горбач, 1998). При этом допускали, что особи, вышедшие из куколок с момента начала лёта до второго отлова (первой даты, для которой значение Ni может быть оценено по формуле), не погибали и не эмигрировали, а со времени последнего отлова с рассчитанным числом Bi до окончания лёта в популяции не появлялись новые особи. Ошибку вычисляли как SEобщ = N(SE)общ – Nобщ, где N(SE)общ = (N2 + SE2) + Σ((Ni+1 + SEi+1) – øi (Ni + SEi – ni + si)). Другой способ оценки общей численности предложил В. Ватт с соавторами (Watt et al., 1977): Nобщ = (1 – ø) Σ Ni, где ø – средняя арифметическая коэффициентов убывания численности øi. Стандартную ошибку SEобщ рассчитывали, руководствуясь описанным выше подходом, где N(SE)общ = (1 – ø) Σ (Ni + SEi). Подставив найденное значение коэффициента ø в выражение T = – (ln ø)–1, можно определить среднюю продолжительность присутствия особи на исследуемой территории в днях (Cook et al., 1976). Однако более адекватной переменной для расчета времени является значение коэффициента ежедневного убывания численности, поскольку он в меньшей степени зависит от величины интервалов между отловами. В настоящей работе мы рассчитывали T, подставляя в указанную выше формулу средние значения øi1/t, где t – число дней между i и i + 1. Иные, более сложные алгоритмы вычислений, рассмотрены у Б. Табашника (Tаbashnik, 1980).
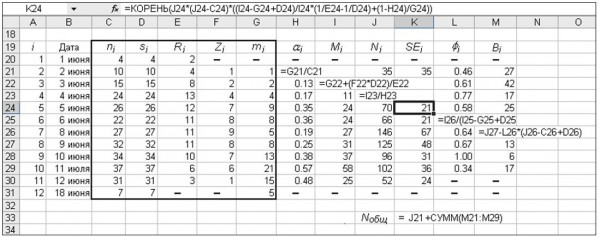
Рис. 4. Расчет демографических параметров по модели Джолли – Себера в среде MS Excel. Рамкой выделен блок исходных переменных (рис. 3), обозначения даны в тексте
Fig. 4. Calculation of the demographic parameters by the Jolly – Seber model in MS Excel. Frame allocates a block of original data (from fig. 3). αi is proportion of marked individuals in sample ni; Mi is the total number of marked individuals in the population on day i ; Ni is estimate of daily numbers; SEi is standard error of Ni; øi is residence rate from day i to i+1; Bi is number of individuals which replenished the population at same time; Nобщ is estimate of the total number of the population
Практическое применение метода Джолли – Себера показало, что модельные параметры зачастую принимают биологически некорректные значения. Так, коэффициент øi порой оказывается больше единицы, что означает, что к моменту времени i + 1 на территории, занимаемой популяцией, осталось больше особей, чем их было в момент времени i. Число прибывших бабочек (Bi) при этом часто становится отрицательным, а общая численность может быть меньше числа отловленных особей. Один из таких вариантов показан на рис. 5: отрицательное значение Bi для 3 июля стало причиной заниженной оценки общей численности популяции. Для оптимизации модели использовали программу «Поиск решения» пакета MS Excel. Ввод ограничений для переменных øi и Bi позволил улучшить результаты вычислений. В некоторых специальных пакетах, например в программе MARK, реализована аналитическая процедура коррекции коэффициентов убывания численности.
Результаты
Основными демографическими показателями, вычисляемыми методом Джолли – Себера, являются общая численность и половой состав популяции, оценки абсолютной численности для каждой даты исследования, коэффициенты, измеряющие скорость убывания популяции вследствие гибели и эмиграции особей, и время присутствия особи на исследуемой территории. Рассмотрим каждую из этих характеристик на примере исследованных нами видов бабочек. Исходные выборки, полученные в результате эксперимента по мечению особей, содержали информацию о числе отловов каждой особи и времени между этими отловами (табл. 1, рис. 3). Динамика численности популяции в течение репродуктивного периода, рассчитанная по соответствующим алгоритмам (рис. 4), показана на примере перламутровки B. aquilonaris (рис. 6). Для значений численности имаго, вычисленным по формулам, даны величины стандартных ошибок (SEi, у самцов и самок эти значения опущены), в остальных случаях Ni = ni. Таким образом, лёт бабочек продолжался 29 дней в 1995 году и 37 дней в 1996 году. Падение численности популяции в середине июля 1996 года была связано с похолоданием, последовавшим за появлением первых особей. Это привело к задержке вылета имаго и к увеличению репродуктивного периода. Вместе с тем продолжительность массового лета оставалась постоянной. Массовый лет длился около 10 дней: с 28 июня по 8 июля в 1995 году и с 24 июля по 1 августа в 1996 году.
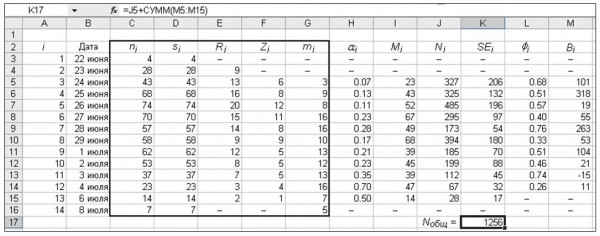
Рис. 5. Настройка параметров модели, описывающей сезонную динамику численности самцов перламутровки Boloria eunomia на болоте Близкое в 1996 году. В ячейке M13 значение Bi = –15 (a), после настройки Bi > 0 во всех случаях (б), соответственно, выросла оценка общей численности (Nобщ). Ф – значение невязки, другие обозначения даны в тексте
Fig. 5. Setting parameters of the model, which describes the seasonal dynamics of male of fritillaries Boloria eunomia on mires “Blizkoe” in 1996. There is Bi = –15 in table cell M13 (а) and Bi > 0 after setting (б). The result of the total number has increased (Nобщ). Ф is value of the residual, other symbols are given in tables 3 and 4.
Таблица 1. Данные об отловах имаго четырех видов булавоусых чешуекрылых
nm – число меченых особей; nr – число повторно отловленных особей; n – число повторных отловов; T – число дней между последовательными отловами особи: Tmax – максимальные значения; M – средняя арифметическая; S – стандартное отклонение; Me – медиана.
Table 1. The total data on mark-release-recapture of four species of butterflies
nm is the number of marked individuals; nr is the number of recaptured individuals; n is the number of recaptures; T is the number of days between consecutive captures: Tmax is the maximum values; M is the mean; S is the standard deviation; Me is median value.
| Показатель | L. populi,
1995 г. |
B. eunomia,
1995 г. |
B. aquilonaris,
1996 г. |
P. mnemosyne,
2003 г. |
||||
| Самцы | Самки | Самцы | Самки | Самцы | Самки | Самцы | Самки | |
| nm | 118 | 5 | 316 | 314 | 690 | 514 | 237 | 96 |
| nr | 23 | – | 71 | 76 | 114 | 87 | 106 | 39 |
| n | 25 | – | 77 | 83 | 122 | 92 | 151 | 56 |
| Tmax | 7 | – | 10 | 11 | 12 | 10 | 22 | 19 |
| MT | 3.0 | – | 3.7 | 3.2 | 3.5 | 3.0 | 5.0 | 5.6 |
| ST | 2.0 | – | 2.3 | 2.6 | 2.5 | 1.6 | 3.8 | 4.0 |
| MeT | 2 | – | 4 | 2 | 2 | 2 | 5 | 5 |
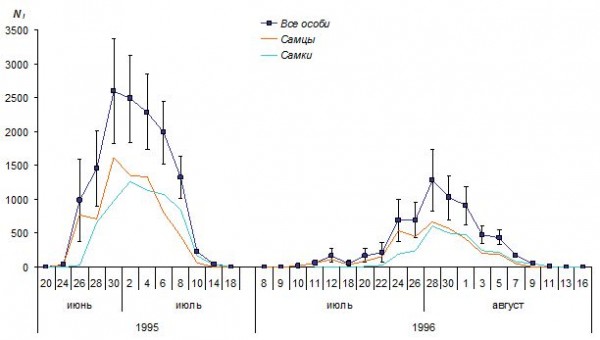
Рис. 6. Динамика численности имаго перламутровки Boloria aquilonaris на болоте Близкое
Fig. 6. The dynamics of adult fritillary Boloria aquilonaris on mires Blizkoe. Lines are all individuals, males and females from top to bottom, respectively
Динамика численности самцов отличалась от динамики численности самок. Самцы появлялись на 3–4 дня раньше самок. Причем вылет самцов происходил одновременно с появлением первых цветущих растений сабельника, а вылет самок – с началом его обильного цветения. Устойчивое снижение численности бабочек совпадало с окончанием массового цветения этого растения. В первой половине лета в составе населения исследуемой территории преобладали самцы, в конце лета более многочисленными были самки. Их лёт длился примерно на неделю дольше лета самцов.
Изучение динамики численности имаго трех видов перламутровок показало, что с мая по август B. freija, B. eunomia и B. aquilonaris последовательно сменяли друг друга (рис. 7). Перекрывание периодов лёта было незначительным. Численность нарастала в направлении от B. freija к B. aquilonaris (табл. 2). Соотношение самцов и самок в исследованных популяциях варьировало от 1.2 : 1 до 1.9 : 1. Подгонка параметров модели под биологически разумные значения привела к незначительной коррекции оценок. Значения коэффициентов убывания численности оставались относительно постоянными. Рассчитанное по этим коэффициентам время присутствия особи на исследуемой территории достигало 3 дней. Близкие значения получены и в эксперименте, при этом максимальные время между отловами особи составляло от 7 до 12 дней.
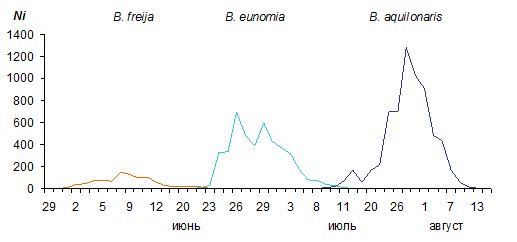
Рис. 7. Смена сезонных аспектов населения перламутровок на болоте Близкое в 1996 году
Fig. 7. Changing seasonal aspects of the fritillary population on mires Blizkoe in 1996
Таблица 2. Общая численность, коэффициент ежедневного убывания и время присутствия особи на исследуемой территории у трех видов перламутровок в 1996 году
1) общая численность (Nобщ) рассчитана по исходной модели (рис. 5а), 2) оценки после настройки параметров модели (рис. 5б), 3) по Watt et al, 1977 после настройки. øi1/t – коэффициент ежедневного убывания численности, T – время присутствия особи на исследуемой территории, M – средняя арифметическая; S – стандартное отклонение, TM и Tmax – среднее и максимальное число дней между отловами особи.
Table 2. Total number, residence rate and residence time of three species of fritillaries on mires “Blizkoe” in 1996
| Показатель | B. freija | B. eunomia | B. aquilonaris | ||||
| Самцы | Самки | Самцы | Самки | Самцы | Самки | ||
| 1 | Nобщ, экз | 200 | 111 | 1256 | 893 | 2041 | 1590 |
| 2 | Nобщ, экз | 216 | 114 | 1299 | 893 | 2041 | 1590 |
| SEобщ, экз | 121 | 61 | 555 | 449 | 1028 | 783 | |
| ♂ : ♀ | 1.9 : 1 | 1.5 : 1 | 1.3 : 1 | ||||
| 3 | Nобщ, экз | 181 | 95 | 1292 | 853 | 1882 | 1599 |
| SEобщ, экз | 99 | 53 | 557 | 414 | 936 | 800 | |
| ♂ : ♀ | 1.9 : 1 | 1.4 : 1 | 1.2 : 1 | ||||
| øi1/t | M | 0.65 | 0.70 | 0.53 | 0.57 | 0.70 | 0.62 |
| S | 0.18 | 0.22 | 0.14 | 0.16 | 0.10 | 0.06 | |
| T, дни | 2.3 | 2.8 | 1.6 | 1.8 | 2.8 | 2.1 | |
| TM, дни | 2.8 | 2.9 | 2.5 | 2.4 | 3.5 | 3.0 | |
| Tmax, дни | 7 | 8 | 12 | 8 | 12 | 10 | |
Обсуждение
Практика применения рассмотренной методики выдвигает на первый план проблему адекватного выбора объекта для популяционного исследования. Первое по важности условие состоит в том, чтобы исследуемая группировка булавоусых чешуекрылых была локализована в пределах одного или нескольких местообитаний с четко выраженными границами (остров, луг, болото, вырубка и др.). Практически все известные исследования выполнены именно на таких экспериментальных площадках (Settele et al., 2009). Предпринятая нами попытка подтвердить гипотезу об оседлом образе жизни глазка цветочного Aphantopus hyperantus (L.) путем мечения на четырех небольших участках сообщающихся между собой обширных лугов закончилась неудачей: из 400 меченых особей повторно была отловлена лишь одна. Основная причина заключалась в быстрой смене населения на исследованных участках. Среда, по-видимому, никак не ограничивала процессы расселения, бабочки везде могли найти необходимые ресурсы для питания и откладки яиц (Горбач, 2012). Результаты изучения популяций того же вида во фрагментированных ландшафтах были иными. Так, эксперимент с мечением бабочек на лесном лугу в Восточной Англии дал достаточное число повторных отловов, чтобы можно было получить серию оценок абсолютной численности (Pollard, 1977). В сельскохозяйственном ландшафте на севере Швейцарии, где глазок концентрируется на непригодных для обработки участках, разбросанных меж полей и каналов, число повторных отловов доходило до 60 % (Biletter et al., 2003). Исследование, проведенное в Юго-Восточной Финляндии (Valtonen, Saarinen, 2005), показало, что бабочки достаточно долго остаются и в придорожных биотопах, ограниченных древостоями. Из 2000 меченых здесь экземпляров удалось повторно отловить около 17 %. Помимо пространственной локализации, успех предприятия не в последнюю очередь зависит и от величины местообитаний: на больших площадях следует ожидать снижения частоты повторных отловов. Так, у перламутровок B. eunomia и B. aquilonaris, которых мы изучали на болоте размером более 50 га, отношение числа повторных отловов к числу повторно отловленных особей равнялось единице (табл. 1: n/ nr ≈ 1), а у парусника P. mnemosine в местообитаниях общей площадью менее 20 га это произведение приближалось к 1.5. В тех случаях, когда виды приурочены к небольшим обособленным местообитаниям, вклад меченых особей может достигать 50 и даже 70 % (Hanski et al., 1996; Musson et al., 1999; Wahlberg et al., 2002). Заметное снижение числа повторных отловов обычно происходит после длительных пауз, возникающих из-за ухудшения погодных условий, но, как показывает опыт, даже двухнедельный перерыв не приводит к полному исчезновению меченых особей с исследуемой территории (Горбач, Кабанен, 2009). И, наконец, численность населения не должна быть слишком низкой или слишком высокой. При низкой численности, как правило, возникают пропуски повторных отловов, из-за которых впоследствии невозможно выполнить расчеты. При высокой численности приходится метить большое число бабочек, в результате неоправданно возрастает продолжительность и трудоемкость работ. Оптимальное число отлавливаемых особей составляет 50–150 экз. в день на одного исследователя. Во время массового лёта перламутровки B. aquilonaris нам удавалось метить по 300 бабочек, но на это уходил целый день. Подобное затягивание работ рискованно, поскольку непредвиденная смена погоды может прервать их, не дав сформировать полноценную выборку. Само собой разумеется, что отловы необходимо производить, затрачивая каждый раз равные усилия и по возможности охватывая всю площадь исследуемого биотопа. Выборки, полученные в разные дни, не должны сильно отличаться по объему, если нет заметного роста или падения численности населения.
Оценки абсолютной численности булавоусых чешуекрылых обычно хорошо согласуются с данными об относительной плотности, получаемыми при учетах имаго на трансектах. Так, E. Поллард (Pollard, 1977), используя для изучения динамики популяций сенницы Coenonympha pamphilius (L.) и глазка A. hyperantus метод Джолли – Себера и метод трансект, указал на значимую сопряженную изменчивость тестируемых переменных (значения коэффициентов корреляции (r) варьировали от 0.55 до 0.76 при p < 0.001). Для популяции червонца Lycaena virgaurea (L.) коэффициент корреляции аналогичных оценок составил 0.92 (Douwes, 1970), для популяции перламутровки Boloria selene (D.S.) – от 0.87 до 0.89 (Douwes, 1976). Полученные значения во всех случаях значимо отличались от нуля (p < 0.001). Повторив эксперимент с одной из колоний парусника P. mnemosyne, мы пришли к аналогичным выводам (рис. 8: r > 0.96, df = 12, p < 0.001). Оценки численности, полученные при пересчете на площадь местообитания, в пяти случаях из восьми не выходили за пределы стандартных ошибок модельных значений. Неожиданно сильная взаимосвязь между переменными, по-видимому, обусловлена оседлостью бабочек и их относительно равномерным размещением на небольшой по размеру территории (Горбач, 2013).
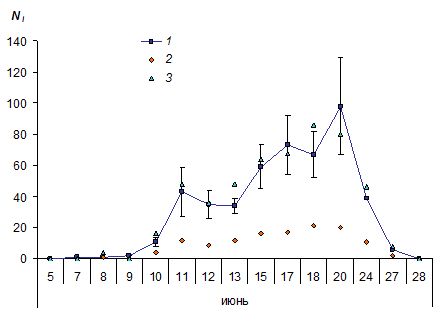
Рис. 8. Динамика численности парусника Parnassius mnemosyne: 1 – Ni ± SEi, рассчитанные методом Джолли – Себера по результатам мечения особей; 2 – число особей, зарегистрированных на трансектах; 3 – то же в пересчете на общую площадь местообитания
Fig. 8. The dynamics of adult clouded Apollo Parnassius mnemosyne: 1 – daily number of individuals (Ni ± SEi), calculated by the Jolly – Seber method; 2 – number of individuals, which were counted by transects; 3 – number of individuals after conversion transect data to total square of the habitat
Для адекватной оценки демографических параметров по данным об отловах рекомендуется использовать выборки с числом особей, помеченных к моменту времени i (mi), не менее 10. Коэффициент ежедневного убывания численности (øi) в таких случаях обычно принимает значения в диапазоне до 1. Незначительные превышения могут возникать лишь в краткие периоды быстрого нарастания численности, когда происходит массовый вылет имаго. Подгонка параметров модели под биологически разумные значения актуальна прежде всего для малых выборок, когда невозможно выполнить условие mi > 10, например при изучении небольших группировок вида в пространственно разобщенных популяциях (метапопуляциях – Хански, 2010). Другая проблема связана с определением численности для первой (i = 1) и последней (i = l) дат исследования. Поскольку эти значения невозможно вычислить по модели, предложено использовать методы экстраполяции (Колли, 1979). Оценку численности во время первого отлова, например, можно получить, предположив равенство скоростей роста в начальный период лета имаго: (lnN3 – lnN2) / t23 = (lnN2 – lnN1) / t12, где t23 и t12 время в днях между вторым и третьим, первым и вторым отловами соответственно. Значения N2 и N3 известны, следовательно, можно вычислить N1. Точно таким же способом определяют Nl для последнего отлова. Этот подход, в основу которого положена классическая экспоненциальная модель роста, на практике зачастую не оправдывает себя. Дело в том, что реальная скорость увеличения численности имаго в начальный период лета может быть столь высока, что оценка для первой даты оказывается существенно меньше числа отловленных особей. В самом конце эксперимента, наоборот, скорость уменьшения численности бывает такой низкой, что экстраполяция дает завышенные оценки, откладывая дату завершения лета на неправдоподобно большой срок. Мы видим два возможных выхода из такой ситуации. Первый заключается в том, чтобы использовать среднюю скорость, вычисленную для более широкого, чем в оригинале, диапазона, например для начального периода от N2 до N4 или даже до N5. Второй подход, реализованный в данной работе, предполагает, что N1 = n1 и Nl = nl. Численность имаго в крайние даты обычно невелика, поэтому погрешности таких допущений не являются критическими.
Использованный нами способ определения коэффициента ежедневного убывания численности популяции (øi1/t) также отличается от других подходов простотой вычислений. Единственным эмпирическим показателем, по которому можно судить об адекватности оценок øi1/t, а значит и øi, является среднее число дней между отловами меченых особей. Этот показатель должен коррелировать со временем, вычисленным по средней от øi1/t, и быть больше него по значению, так как в последнем случае речь идет обо всех особях, в том числе и тех, что не попались ни разу или пропали сразу после мечения. Выдвинутым требованиям, как правило, отвечают все известные варианты коэффициентов ежедневного убывания численности (Tabashnik, 1980), поэтому невозможно оценить преимущества тех или иных подходов по существу. И поскольку применение сложных алгоритмов на практике не гарантирует большей точности оценок, то простые методы кажутся более предпочтительными. Значимость отличий численности самцов и самок оценивают, сравнивая модельные значения Nmi и Nfi с альтернативным распределением частот (критерий χ2).
Заключение
Метод Джолли – Себера является одним из наиболее информативных способов описания хода демографических процессов в популяциях. По частоте повторных отловов меченых особей данный подход позволяет получать серии значений абсолютной численности, оценивать интенсивность элиминации и пополнения популяции за время между посещениями исследуемой территории. К исследованию популяций бабочек метод Джолли – Себера подходит лучше других: в условиях, когда за относительно короткое время численность имаго сначала многократно увеличивается, а затем падает до нуля, адекватность оценок могут обеспечить лишь отловы, многократно повторяемые на протяжении всего периода лета. Наиболее важными показателями, которые вычисляют, опираясь на полученные переменные, являются общая численность и соотношение полов. Ежедневная элиминация в изученных популяциях бабочек оценивается в 30–50 % особей в среднем за сезон. Сравнение коэффициентов убывания численности, полученных, например, для разных сезонов и популяций или для близкородственных видов, населяющих одно и то же местообитание, может быть весьма полезным, особенно если имеются данные о пространственной структуре изучаемых группировок и перемещениях особей. Использование MS Excel позволяет лучше понять суть производимых вычислений и в случае необходимости настраивать модельные параметры, используя процедуру оптимизации.
Библиография
Горбач В. В. Внутрипопуляционная изменчивость элементов рисунка на крыльях глазка цветочного Aphantopus hyperantus (Lepidoptera, Satyridae) // Уч. зап. Петрозав. гос. ун-та. 2011. № 6. С. 27–31.
Горбач В. В. Пространственная структура популяции и подвижность имаго перламутровки Boloria aquilonaris (Lepidoptera, Nymphalidae) // Экология. 2011. № 4. С. 289–296.
Горбач В. В. Сезонная динамика численности и половой состав популяции перламутровки Boloria aquilonaris (Lepidoptera, Nymphalidae) // Зоол. журн. 1998. Т. 77, № 5. С. 576–581.
Горбач В. В. Фауна и экология булавоусых чешуекрылых (Lepidoptera: Hesperioidea et Papilionoidea) Карелии . Петрозаводск: Изд-во ПетрГУ, 2013. 254 c.
Горбач В. В., Кабанен Д. Н. Пространственная организованность популяции черного аполлона (Parnassius mnemosyne) в условиях Заонежья // Зоол. журн. 2009. Т. 88, № 12. С. 1493–1505.
Горбач В. В., Сааринен К., Резниченко Е. С. К экологии тополевого ленточника Limenitis populi (Lepidoptera, Nymphalidae) Восточной Фенноскандии // Зоол. журн. 2010. Т. 89, № 11. С. 1340–1349.
Коли Г. Анализ популяций позвоночных. М.: Мир, 1979. 362 с.
Хански И. Ускользающий мир: экологические последствия утраты местообитаний. М.: Т-во науч. изданий КМК, 2010. 340 с.
Arnason A. N., Schwartz C. J. Using POPAN-5 to analyse banding data // Bird Study. 1999. V. 46, Suppl. S. 157–168. URL: http://www.cs.umanitoba.ca/~popan/ .
Billeter R., Sedivy I., Diekotter T. Distribution and dispersal patterns of the ringlet butterfly (Aphantopus hyperantus) in an agricultural landscape // Bulletin of the Geobotanical Institute ETH. 2003. V. 69. P. 45–55.
Brussard P. F., Ehrlich P. R. Adult behavior and population structure in Erebia epipsodea (Lepidoptera: Satyrinae) // Ecology. 1970. V. 51, №. 5. P. 880–885.
Cook L. M., Brower L. P., Croze H. J. The accuracy of a population estimation from multiple recapture data // J. Anim. Ecol. 1967. V. 36, № 1. P. 57–60.
Douwes P. Size of, gain to and loss from a population of adult Heodes virgaurea L. (Lep., Lycaenidae) // Entomol. Scand. 1970. V. 1. P. 225–247.
Douwes P. An area census method for estimating butterfly population numbers // J. Res. Lepid. 1976. V. 15, № 3. P. 146–152.
Dowdeswell W. H., Fisher R. A., Ford E. B. The quantitative study of population in the Lepidoptera. 1. Polyommatus icarus Rott. // Ann. Eugenics. 1940. V. 10, № 1. P. 123–136.
Dowdeswell W. H., Fisher R. A., Ford E. B. The quantitative study of population in the Lepidoptera. 2. Maniola jurtina L. // Heredity. 1949. V. 3, № 1. P. 67–84.
Ehrlich P. R. Intrinsic barriers to dispersal in checkerspot butterfly // Science. 1961. V. 134. P. 108–109.
Ehrlich P. R., Davidson S. E. Techniques for capture-recapture studies of Lepidoptera populations // J. Lepidopt. Soc. 1960. V. 14. P. 227–229.
Ehrlich P. R., Hanski I. (eds.) On the wings of checkerspots: a model system for population biology. Oxford: Oxford University Press, 2004. 371 p.
Ehrlich P. R., Raven P. H. The differentiation of populations // Science. 1969. V. 165. P. 1228–1232.
Ford H. D., Ford E. B. Fluctuation in numbers, and its influence on variation, in Melitaea aurinia Rott. (Lepidoptera) // Trans. R. Entomol. Soc. Lond. 1930. V. 78, № 2. P. 345–351.
Gall L. F. The effects of capturing and marking on subsequent activity in Boloria acrocnema (Lepidoptera: Nymphalidae), with a comparison of different numerical models that estimate population size // Biol. Conserv. 1984. V. 28, № 2. P. 139–154.
Hanski I., Kuussaari M., Nieminen M. Metapopulation structure and migration in the butterfly Melitaea cinxia // Ecology. 1994. V. 75, № 3. P. 747–762.
Harding P. T., Green S. V. Recent surveys and research on butterflies in Britain and Ireland: a species index and bibliography. Hantingdon: Biological Records Centre, 1991. 42 p.
Jolly G. M. Explicit estimates from capture-recapture data with both death and immigration – stochastic model // Biometrika. 1965. V. 52, № 1–2. P. 225–247.
Mousson L., Nève G., Baguette M. Metapopulation structure and conservation of the cranberry fritillary Boloria aquilonaris (lepidoptera, nymphalidae) inBelgium. // Biol. Conserv. 1999. V. 87, № 3. P. 285–293.
Pollard E. A method for assessing changes in the abundance of butterflies // Biol. Conserv. 1977. V. 12, № 2. P. 115–134.
Pollock K. H., Nichols J. D., Brownie C., Hines J. E. 1990. Statistical inference for capture-recapture experiments // Wildlife Monographs. 1990. V 107. 97 p. URL: http://www.mbr-pwrc.usgs.gov/software/jolly.html .
Seber G. A. F. A note the multi-sample recapture census // Biometrika. 1965. V. 52, № 1–2. P. 249–259.
Settele J., Shreve T., Konvička M., Van Dyck H. (eds.). Ecology of Butterflies in Europe. Cambridge: Cambridge University Press, 2009. 526 p.
Singer M. C., Wedlike P. Capture does affect probability of recapture in a butterfly species // Ecol. Entomol. 1981. V. 6, № 2. P. 215–216.
Tabashnik B. E. Population structure of pierid butterflies, III. Pestpopulation of Colias philodice eriphyle // Oecologia. 1980. V. 47, № 2. P. 175–183.
Valtonen A, Saarinen K. A highway intersection as an alternative habitat to a meadow butterfly: effect of mowing, habitat geometry and roads on the ringlet (Aphantopus hyperantus) // Ann. Zool. Fenn. 2005. V. 42, № 5. P. 545–556.
Wahlberg N., Klemetti T., Selonen V., Hanski I. Metapopulation structure and movements in five species of checkerspot butterflies // Oecologia. 2002. V. 130, № 1. P. 33–43.
Watt W. B., Chew F. S., Snyder L. G. F., Watt A. G., Rothschild D. E. Population structure of pierid butterflies. I. Numbers and movements of some montane Colias species // Oecologia. 1977. V. 27, № 1. P. 1–22.
White G. C., Burnham K. P. Program MARK: survival estimation from population of marked animals // Bird Study. 1999. V. 46, Suppl. S. 120–139. URL: http://warnercnr.colostate.edu/~gwhite/mark/mark.htm .






 © 2011 - 2026
© 2011 - 2026