Коросов А. В. Нейронные сети для экологии: введение // Принципы экологии. 2023. № 3. С. 76–96. DOI: 10.15393/j1.art.2023.14002

Выпуск № 3

Методы экологических исследований

pdf-версия статьи

57.087.1 :519

Нейронные сети для экологии: введение

Введение

Несмотря на обилие публикаций о нейронных сетях, в экологических исследованиях этот математический аппарат используется односторонне. Беглый анализ литературы показывает, что в основном с помощью нейронных сетей с экологическими целями выполняют дешифрирование космических снимков и проводят анализ распространения промышленных поллютантов. В области биологической экологии такого рода исследования крайне редки (Шитиков и др., 2003; Скворцов, 2018). Вероятно, одной из причин является отсутствие понятных методических руководств, объясняющих смысл этой процедуры на примерах из экологии. Нам представляется, что начинать объяснение этого метода следует не с введения в морфологию нейрона, но с поиска математических аналогий, уже известных биологам. Если за старт взять понятие линейной регрессии, картина может проясниться быстрее (Каллан, 2001). Появляется возможность, постепенно дополняя методическую базу, подготовить читателей к использованию нейронных сетей как эффективного инструмента моделирования экологических явлений. Статья написана для популяризации метода нейросетевого моделирования среди специалистов в области биологии и экологии.

Целью работы мы ставим объяснение основ нейросетевого моделирования через понятие регрессии и демонстрацию его использования в некоторых областях экологии животных.

Преследуя только эту цель, мы не будем рассматривать методы оценки статистической значимости модельных параметров. Примеры проиллюстрированы расчетами в среде языка R (The R…, 2023), который широко используется в биометрии (Мастицкий, Шитиков, 2014; Якимов, 2019; Коросов, Горбач, 2017, 2021), в т. ч. и для построения нейросетей (Шитиков, Мастицкий, 2017; Машинное обучение..., 2020; Ashirali, 2023). Для лучшего усвоения метода читателям необходимо самостоятельно выполнить представленные скрипты в среде R; исходные данные для расчетов либо прописаны в скрипте, либо прикреплены к тексту в виде файлов (загрузка по гиперссылке).

Традиционные методы исследований

Для понимания существа искусственной нейронной сети необходимо рассмотреть основные понятия регрессионного анализа (Иванова и др., 1981; Мастицкий, Шитиков, 2014; Ивантер, Коросов, 2017).

 Линейная регрессия

Регрессионный анализ изучает зависимость некоей характеристики (случайной величины y) от другой характеристики (случайной величины x) (или от нескольких характеристик). Для обозначения независимых переменных (x) в регрессионном анализе используют термин предикторы, а при нейросетевом моделировании – ковариаты. Зависимость y от x может проявляться, когда есть выборка нескольких биологических объектов, у которых определены показатели, имеющие разные значения. Например, масса (y), как правило, выше у особей с большей длиной тела (x). Отдельную i-я особь характеризуют два промера (x_i, y_i), на диаграмме она представлена точкой с этими координатами, а вся выборка из n особей предстает размытым облаком. Из-за влияния многих (случайных) факторов, данная зависимость не является функциональной. Ее график – это не линия, а эллипс рассеяния, вытянутый в направлении зависимости: например, чем больше длина тела, тем больше масса. При этом оказывается, что каждому значению признака (x_i) соответствует целое множество из k значений признака y_{i(j = 1, 2 ... k)} (рис. 1).

Если мы ставим задачу выразить главную тенденцию связи этих характеристик, то такая неопределенность малопродуктивна: необходимо каждому значению x_i поставить в соответствие какое-то единственное значение y_i. Из математической статистики известно, что согласно методу максимального правдоподобия, наиболее представительной характеристикой выборки является средняя арифметическая ŷ = Σy_j / n. Если для каждого значения x_i рассчитать соответствующее ему значение ŷ_i, и на диаграмму нанести точки с этими координатами (x_i, ŷ_i), то в идеальном случае двумерного нормального распределения все средние точки выстроятся в линию. Таким образом, регрессия – это не просто зависимость одного признака от другого, но зависимость среднего уровня одного признака от другого признака.

 

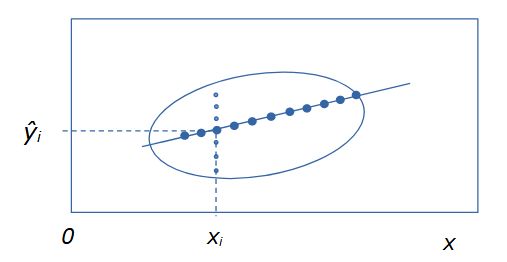
Рис. 1. Эллипс рассеяния вариант для двумерного распределения положительно зависимых признаков y от x. Мелкие точки – множество значений y_ij, соответствующих одному значению x_i. Крупные точки – множество значений частных средних ŷ_i для разных значений x_i

 Fig. 1. Scattering ellipse option for two-dimensional distribution of positively dependent features y on x. Small dots are a set of values y_ij corresponding to one value x_i. Large dots – a set of values of partial averages ŷ_i for different values of x_i

 

Цель регрессионного анализа состоит в том, чтобы все множество этих частных средних заменить линией регрессии, построенной с использованием всего двух значений (a₀ и a₁), параметров линейной модели: ŷ = a₀ + a₁*x.

 Смещение

Параметры регрессионной модели обычно имеют экологический смысл, отражают какой-то внутренний закон формирования вариант. Например, распространение загрязнений (K) вокруг (dist) источника (Рапута и др., 2015) можно было бы описать линейным уравнением (рис. 2):

K = a₀ + (–a₁)*dist .

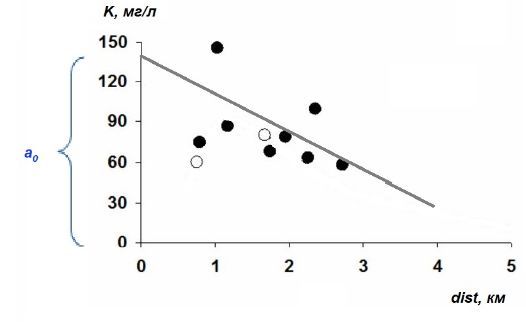
Рис. 2. Линия регрессии, описывающая тренд снижения уровня загрязнения (K) по мере удаления (dist) от источника (ТЭЦ)

 Fig. 2. Regression line describing the trend of decreasing pollution level (K) as the distance (dist) from the source (CHP)

 

Коэффициент a₁ выражает пропорцию между расстоянием и загрязнением, он имеет смысл скорости изменения уровня загрязнения при удалении от его источника (объем поллютанта на единицу расстояния); причем он отрицательный, поскольку с ростом расстояния интенсивность загрязнений снижается. Коэффициент a₀ имеет смысл уровня загрязнения в месте размещения источника, т. е. при нулевом расстоянии от него (a₀ = K_(dist=0)). Линия регрессии не проходит через начало координат, она смещена относительно нуля на величину a₀, по этой причине при нейросетевом моделировании свободный член уравнения a₀ часто называют смещением (или параметром сдвига).

Преследуя наши цели, представим уравнение регрессии в виде блок-схемы, где элементы связаны стрелками (рис. 3). Для наглядности к первому коэффициенту добавим единицу. У этой конструкции есть вход (переменная x и смещение), коэффициенты пропорциональности (параметры a), действия над ними (кружок) и выход (ŷ). Представленный граф уже похож на «нейрон», но еще не обладает всеми его свойствами.

 

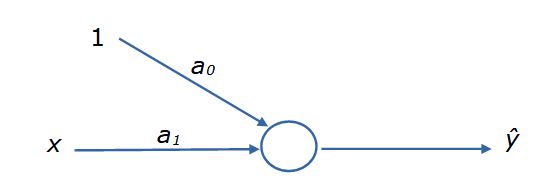
Рис. 3. Блок-схема уравнения регрессии ŷ = a₀*1 + a₁*x

Fig. 3. Flowchart of the regression equation ŷ = a₀*1 + a₁*x

 

Оценка значений a: МНК

Теперь возникает вопрос: как найти значения параметров a₀ и a₁? Один путь состоит в применении аналитического «метода наименьших квадратов» (МНК), который позволяет строить линию регрессии, проходящую точно по середине частных выборок, т. е. линию, которая в наименьшей степени удалена от всех точек выборки. Как можно заметить, частная средняя ŷ_i отличается от многих значений y_ij, полученных при определенном значении x_i, причем разность (y_ij – ŷ_i) будет как положительной, так и отрицательной, а их сумма будет равна нулю. Для учета всех отклонений указанное выражение возводят в квадрат и суммируют по всей совокупности данных:

 ,

для простоты: Σ(y – ŷ)².

Метод определения наименьших квадратов отклонения исходных данных от линии регрессии состоит в том, чтобы подобрать такие коэффициенты a₀ и a₁, при которых выполнится условие:

Σ(y – ŷ)² = Σ(y – a₀ + a₁*x)² = min.

Исходя из этого уравнения, аналитически можно найти производные по a₀ и a₁, приравнять их к нулю для обнаружения экстремума (min) и получить корни – рабочие формулы для расчета коэффициентов регрессии a₀ и a₁. Такие формулы представлены в любом учебнике по статистике. В среде R расчеты по ним выполняет функция lm() (рис. 4). В результате наших расчетов получено уравнение: w’ = 6.36*lt – 240.

 

w←c(85,90,85,95,95,135,165,135,140) lt←c(51,51,52,54,54,59,59,60,62) (lreg←lm(w~lt))    Call:    lm(formula = w ~ lt)    Coefficients:    (Intercept) lt    -240.766 6.358 plot(lt,w) lines(lt,predict(lreg))

 Рис. 4. Расчет линейной регрессии зависимости массы тела (w) гадюки от ее длины (lt)

Fig. 4. Calculation of linear regression of the dependence of the body weight (w) of the viper on its length (lt) 

 

К сожалению, для многокомпонентных моделей в общем случае невозможно найти корни (решения) аналитическим путем. При современном компьютерном моделировании от метода МНК берут только метрику отличий модели от реальности, сумму квадратов отклонений (невязку, или функцию потерь), но используют ее по-иному.

 Оценка значений a: численные методы

Существует и другой путь определения коэффициентов a₀ и a₁ в уравнении регрессии – прямая подгонка методами оптимизации (минимизации) с использованием численных методов и компьютеров. С этой целью сначала задаются любые (случайные или биологически правдоподобные) стартовые значения коэффициентов a. Затем рассчитываются значения ŷ и вычисляется невязка, равная сумме квадратов отклонения точек от линии регрессии: S = Σ(y – ŷ)². Затем с учетом полученной невязки параметры a₀ и a₁ некоторым образом переопределяются, вновь рассчитываются значения ŷ, вновь рассчитывается невязка и т. д. Процедура повторяется в стремлении минимизировать функцию невязки (S→0) и заканчивается, когда эта функция перестает уменьшаться. Разработано множество численных методов (алгоритмов) минимизации (Ньютона, градиентный спуск и др.), быстро приводящих к результату – нахождению лучших значений параметров модели, максимально близкой к эмпирическим значениям. Таким путем можно найти параметры как линейных, так и криволинейных зависимостей (степенных, экспоненциальных, гиперболических, логистических и пр.). В среде R подгонку параметров модели можно выполнить с помощью функций nls(), nlm(), optim() и др. Для линейной модели подгонка дает точно такие же результаты, что и МНК: w’ = 6.36*x – 240.

  

nls(w~a0+a1*lt, start=list(a0=1,a1=1))    Nonlinear regression model    model: w ~ a0 + a1 * lt    data: parent.frame()    a0 a1    -240.766 6.358    residual sum-of-squares: 1335    Number of iterations to convergence: 1    Achieved convergence tolerance: 1.403e-08

Рис. 5. Расчет линейной регрессии методом подгонки

Fig. 5. Calculation of linear regression by fitting method

 

Прямая подгонка с помощью указанных функций позволяет оценивать параметры уравнений различного вида и строить весьма сложные модели (Меншуткин, 2010). Этот метод использовался и для настройки первых вариантов нейронных сетей, однако при усложнении их структуры подгонка перестала справляться с задачей поиска адекватных параметров.

 Множественная регрессия

Помимо зависимости одной переменной от другой, регрессионный анализ позволяет изучать зависимость одной переменной (y) от многих (x₁, x₂, x₃ …) – это множественный регрессионный анализ. Такие задачи решают функции lm() (для нормального распределения) и glm() (для многих других типов распределения) (рис. 6). Расчеты для нашего примера позволили составить уравнение множественной регрессии: w’ = 6.03*lt -0.315*lc –191.

  

w←c(40,156,105,85,80,50,75,48,75,67) lt←c(44,59,49,50,54,43,49,42,47,47) lc←c(70,78,66,90,83,70,62,75,40,80) glm(w~lt+lc)    Call: glm(formula = w ~ lt + lc)    Coefficients:    (Intercept) lt lc    -191.298 6.031 -0.315    Degrees of Freedom: 9 Total (i.e. Null); 7 Residual    Null Deviance: 10130    Residual Deviance: 1897 AIC: 88.83

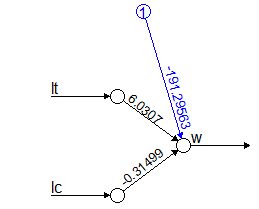Рис. 6. Расчет множественной регрессии с помощью функции glm()

Fig. 6. Calculation of multiple regression using the glm() function

 

Для наглядного отображения взаимосвязи изучаемых переменных в общем уравнении диаграммы мы воспользовались пакетом neuralnet (скрипт не приводится). Диаграмма для множественной регрессии на рис. 6 вплотную подводит к понятию сети как множества взаимосвязанных компонентов модели. Вершины (кружки) символизируют значения исходных и расчетных переменных. Связывающие их дуги (стрелки) символизируют структуру уравнений, а числа над ними – коэффициенты пропорциональности (параметры).

 Криволинейная регрессия

Зависимости между экологическими характеристиками редко имеют линейную форму. Чаще всего для двух изучаемых характеристик характерна аллометрия – разная скорость или масштаб их изменения. Это порождает ту или иную нелинейность, которую точнее воспроизводят различные криволинейные функции – степенная, показательная, параболическая и пр. Общий алгоритм для оценки параметров криволинейной регрессии состоит из этапов (1) «выпрямления» графика зависимости за счет преобразования исходных характеристик, (2) поиска параметров линейной модели и (3) обратного преобразования полученных коэффициентов. Например, для степенной модели (ŷ = a₀*x^a1) находят параметры (A) линейной модели для прологарифмированных исходных данных ln(y) = A₀ + A₁*ln(x), которые затем преобразуют обратно a₀ = e^A0, a₁ = A₁ (рис. 7). Для нашего примера результирующее уравнение криволинейной (степенной) регрессии имеет вид: w’ = 0.000378 * lt^3.137.

  

w←c(85,90,85,95,95,135,165,135,140) lt←c(51,51,52,54,54,59,59,60,62) a←(cm←lm(log(w)~log(lt)))$coefficients a[1]←exp(a[1]) a   (Intercept) log(lt)    0.0003781285 3.1317477923 plot(lt,w) lines(lt,a[1]*lt^a[2])

Рис. 7. Расчет степенной функции зависимости массы от длины тела гадюки

Fig. 7. Calculation of the power function of the dependence of the mass of the viper on its body length

 

Логистическая регрессия

Среди различных нелинейных взаимодействий в экологии часто встречается логистическая зависимость, которую можно описать с помощью логистической регрессии. График этой функции (рис. 8) имеет s-образую форму с двумя перегибами и соответствует трем состояниям изучаемой системы. При возрастании действия существенного фактора (x) на биосистему ее характеристика (y) вначале не меняются (минимальный уровень), затем на коротком переходном этапе велчина y резко возрастает и стабилизируется на максимальном уровне. Таковы, например, кривые смертности животных в возрастающих дозах токсиканта, степени деградации экосистем при росте антропогенной нагрузки и пр.

Формула логистической регрессии ŷ = C + A / (1 + e^–(a0+a1*x)) включает в себя четыре параметра: C – нижняя граница значений (константа), A – верхняя граница значений (асимптота), a₀, a₁ – коэффициенты пропорциональности. Если исходные данные привести к шкале от 0 до 1 (C = 0, A = 1), уравнение упрощается: ŷ = 1 / (1 + e^–(a0+a1*x)).

В этом выражении мы видим объединение двух формул: линейной регрессии z = a₀ + a₁ * x и логита 1 / (1 + e^–z). В свою очередь, в формулу логита включены две плавные криволинейные функции: гиперболическая (1/x) и показательная (e^–z). Именно их сочетание позволяет учесть два участка перегиба логистической кривой (возрастание и выполаживание): эти функции «выпрямляют» исходные данные и позволяют посчитать линейную регрессию преобразованных значений.

В примере показан расчет смертность дафний (от 0 до 1) в возрастающих концентрациях лигнина от 100 до 1000 мг/л (Коросов, Калинкина, 2003) (рис. 8). Полученное уравнение имеет вид: p = 1/ (1 + e^{–(0.019*K–8.691)}).

 

K←c(100,126,158,200,251,316,398,501,631,794,1000) p←c(0,0,0,0,0,0,0.5,0.5,1,1,1) d←data.frame(K,p) (loreg←glm(p~K, family = binomial(), data=d))    Call: glm(formula = p ~ K, family = binomial(), data = d)    Coefficients:    (Intercept) K    -8.691 0.019    Degrees of Freedom: 10 Total (i.e. Null); 9 Residual    Null Deviance: 11.65    Residual Deviance: 0.7443 AIC: 7.216 plot(d) lines(K,predict(loreg,type="response"))

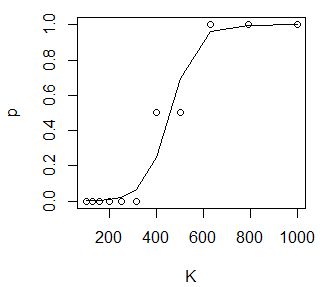 Рис. 8. Расчет логистической регрессии гибели дафний в токсиканте

 Fig. 8. Calculation of logistic regression of the death of daphnia in a toxicant

 

Обобщая содержание раздела, необходимо привести те понятия, которые понадобятся для дальнейшего изложения. В их число вошли: регрессия, переменные (категориальные факторы и непрерывные ковариаты), параметры модели, блок-схема связей между переменными и параметрами, смещение, множественная регрессия, логит, подгонка методами оптимизации, функция потерь.

Оригинальные методы исследований

Искусственные нейронные сети создавались под задачи классификации, когда необходимо тестируемый объект отнести к одной из двух или нескольких известных категорий (Каллан, 2001; Шолле, 2022). Ставилась задача отнести изучаемые объекты к тому или иному классу, используя их различающиеся характеристики. Сложность решения такого рода задач состоит в том, что количественные характеристики объектов нужно преобразовывать в качественные, таксономические. Если в подобном распознающем устройстве (множестве математических формул) на вход подать непрерывные количественные характеристики (замеры, концентрации, цветность, яркость), то на выходе должен быть получен прогноз некой дискретной переменной (номер класса объекта). Иными словами, необходимо плавные изменения аргументов перевести к прерывистые, скачкообразные изменения функции.

 «Нейрон»

Вот здесь и пригодились знания о биологическом нейроне, который работает по закону «все или ничего»: при воздействии внешних факторов нейрон не реагирует до тех пор, пока сумма внешних сигналов не превысит некий порог, после чего нейрон активируется, формирует потенциал действия (электрический импульс) во всей полноте и передает его по аксону к тканям (Шмидт, Тевс, 1996). Таким образом, когда суммарная величина внешних сигналов достигает определенного уровня, нейрон резко меняет свое качество.

Для математической имитации этой ситуации нужно найти такую функцию, которая сохраняет низкий уровень при многих значениях аргумента, но в определенный момент при незначительном приращении аргумента может показать резкое возрастание (и стабилизацию). Одну из таких математических конструкций мы рассмотрели выше ‒ это логистическая регрессия.

В общем смысле можно сказать, что отдельный математический «искусственный нейрон» реализует логистическую регрессию (рис. 9).

Он состоит из двух частей. Первый компонент ‒ это «сумматор», линейное уравнение, обобщающее действие k внешних стимулов:

z = a₀ * 1 + a₁ * x₁ + a₂ * x₂+ … +a_k * x_k .

Второй компонент ‒ это «активатор», уравнение логита, который «решает», достаточно ли велик уровень внешних воздействий, чтобы нейрон на них скачкообразно отреагировал:

ŷ = 1 / (1 + e^–z).

Помимо логита предложен целый ряд других функций активации нейрона, которые мы не рассматриваем.

Конструкцию отдельного «нейрона» можно воспринимать как уравнение линейной регрессии, связывающей некие переменные, дополненное нелинейным членом. Разные ковариаты (переменные x) могут иметь разное влияние на нейрон, что призваны выражать коэффициенты a.

   

 Рис. 9. Схема одного искусственного нейрона

Fig. 9. Diagram of one artificial neuron

 

Рассмотрим, как с помощью нейронов решается типичная задача для нейронной сети: предсказать качество объекта (y’) по набору его количественных характеристик (x). Для решения таких задач из нейронов строят «искусственную нейронную сеть» (ИНС).

 Нейросетевое моделирование

Работа с сетью проходит в четыре этапа: создание, обучение, проверка, использование. Сначала создается структура сети, включающая установление входных и выходных переменных, число скрытых слоев, вид функции активации и пр. В процессе обучения на выборке объектов точно известного качества выполняется поиск значений коэффициентов a для всех связей между переменными. Проверка состоит в определении доли верных прогнозов на выборке объектов точно известного качества, но ранее не включенных в анализ. Во время использования сети в практических целях определяется статус неизвестных объектов.

Представленные ниже расчеты выполнены с использованием функции neuralnet() из пакета neuralnet (краткая запись – пакет::функция() – neuralnet::neuralnet()), который необходимо предварительно получить из репозитария и включить. Примерно те же результаты можно получить, используя функцию nnet::nnet(), RSNNS::mlp(). Результаты работы функции nnet() очень выразительно позволяет отображать функция gamlss.add::plot().

 Модели с одним нейроном

Рассмотрим особенности работы функции neuralnet() на примере уже знакомой задачи определения смертности дафний в растворах лигнина. Функция neuralnet() включает в себя три основных аргумента. Требуется явно указать входные и выходные переменные (formula), источник данных (data) и число (скрытых) слоев нейронов (hidden). В скрипте (рис. 10) помимо этой функции заданы операторы ввода данных и вывода результатов.

 

library(neuralnet) library(neuralnet) K←c(100,126,158,200,251,316,398,501,631,794,1000) p←c(0,0,0,0,0,0,0.5,0.5,1,1,1) d←data.frame(K,p) nv←neuralnet(formula = p~K, data = d, hidden = 0) dn←as.vector(nv$net.result[[1]]) plot(d) lines(K,dn,lty=2) plot(nv)

Рис. 10. Скрипт модели гибели дафний в лигнине

Fig. 10. The script of the model of the death of daphnia in lignin

 

При отсутствии (скрытых) нейронов (hidden=0) функция neuralnet() рассчитывает простую линейную регрессию (рис. 11 А). В этом случае коэффициенты модели имеют биологический смысл, в частности a₁ = 0.0014 доля/концентрация, т. е. приращение концентрации на 100 мг/л влечет приращение доли погибших на 0.14, на 14 %. Можно заметить, что эта модель довольно плохо описывает явление, в частности, по ее прогнозу при концентрациях 1000 мг/л должно погибнуть более 100 % подопытных животных, что абсурдно.

При добавлении нейронов промежуточного (скрытого) слоя (hidden=1...) появляется эффект логит-преобразования – модель имитирует отсутствие смертности до определенного порога и показывает скачкообразный рост смертности при небольшом приросте концентраций токсиканта (рис. 11 Б, В).

 

 

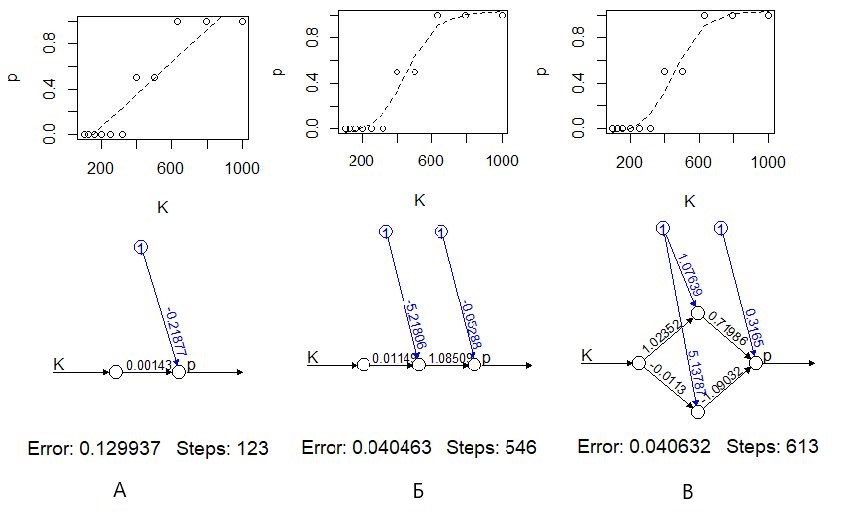
Рис. 11. Моделирование токсического эффекта с помощью нейронной сети без скрытых нейронов (А), с одним скрытым нейроном (Б) и с двумя скрытым нейронами (В)

Fig. 11. Modeling of the toxic effect using a neural network without hidden neurons (А), with one hidden neuron (Б) and with two hidden neurons (В)

 

 Нейронная сеть

Для решения сложных задач нейронные сети формируют из нескольких «слоев», состоящих из нескольких нейронов (рис. 12). Принято считать, что входные переменные x образуют первый (входной) слой. Последний (выходной) слой представляет собой расчетные значения y’, собственно результат работы сети. В эти слои нейроны не входят. Компоненты входного слоя только поставляют данные, а выходной слой служит для обобщения и приведения результатов моделирования к размерности выходной переменной. Второй же и следующие промежуточные (скрытые) слои состоят собственно из нейронов. Каждый нейрон воспринимает сигналы от всех входных элементов и передает собственный сигнал всем следующим элементам. Величина сигнала регулируется коэффициентами пропорциональности. Каскад расчетов начинается со стартовых значений (x) и заканчивается результатом (y’). Такая схема сети, составленной из полносвязных слоев нейронов с прямым распространением сигналов, называется многослойный персептрон (перцептрон).

   

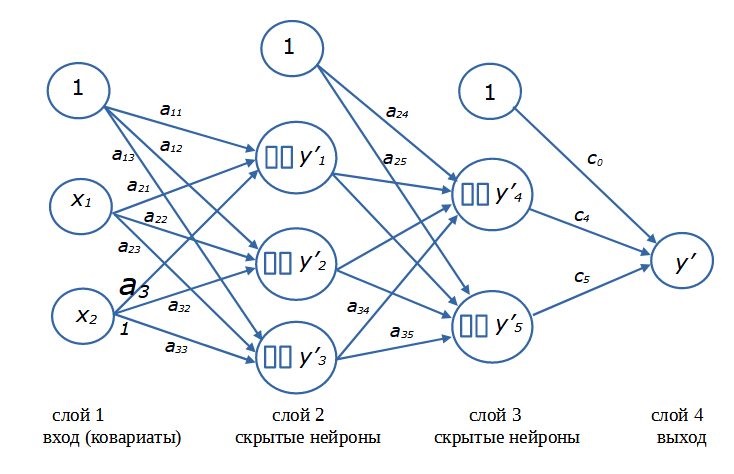
Рис. 12. Схема нейронной сети с двумя скрытыми слоями нейронов

Fig. 12. Diagram of a neural network with two hidden layers of neurons

 

Термин «скрытый» (латентный, внутренний) «нейронный слой» подчеркивает то обстоятельство, что значения как входных (x), так и выходных (y) переменных заданы в явном виде (в виде величин, записанных в файле), чем они и отличаются от расчетных внутри-сетевых переменных (y_i’). Нейрон, как математическая формула, рассчитывает значения внутренних переменных (скрытых в памяти), которые нам в общем-то малоинтересны, поскольку от сети требуется только конечный результат ‒ как можно более точный прогноз значений y. Только в автоассоциативных сетях интерес представляют именно внутренние переменные (Шитиков и др., 2003) (заметим, что функции nnet::nnet() и RSNNS::mlp() позволяют строить такие сети).

Следует отметить, что из-за множества пересекающихся нелинейных связей коэффициенты сети утрачивают биологический смысл, их величина есть всего лишь средство преобразования одних переменных в другие.

 Настройка нейронной сети

Те читатели, которые попробовали применить скрипт для настройки одного нейрона, могут быть удивлены (возмущены) тем, что их расчеты не дают такой же результат, что представлен на рис. 11 Б или В: иногда пунктир не соответствует данным и располагается горизонтально. Причину следует искать в механизме перерасчета коэффициентов нейросети.

Во-первых, стартовые коэффициенты a по умолчанию задаются как случайные величины (хотя их можно специально задать в аргументах функции). Соответственно, разные запуски функции neuralnet() будут приводить к разным результатам; на языке технологии подгонки – «невязка нашла локальный минимум» (неудачное решение). Чтобы прийти к достойному решению (как на рис. 11), нужен многократный перезапуск настройки (с разными случайными стартовыми значениями параметров). Оценка качества полученной модели должна проводиться на другой выборке.

Во-вторых, важно иметь в виду, что на результаты настройки (обучения) сети могут повлиять даже незначительные вариации в исходных данных. Общеизвестно, что от качества и объема стартовой информации зависит работоспособность любой модели, в т. ч. нейронной; сеть можно как «недоучить», так и «переучить». Эти вопросы выходят за рамки нашей цели, однако, варьируя объемы входящей информации в разных прогонах настройки, можно больше понять о существе зависимостей, заключенных в исходных данных. В частности, можно ощутимо уточнить представление о структуре данных, если применить тот или иной вариант ресамплинга (Шитиков, Розенберг, 2013).

В-третьих, нужно помнить, что настройка сети осуществляется сложными числовыми методами со своими особенностями. На раннем этапе развития ИНС определение коэффициентов a выполнялось традиционными числовыми методами, методами прямой подгонки. Для численной оптимизации коэффициентов сети обычно используется алгоритм градиентного спуска, для которого характерны свои проблемы, в частности возможность попасть в локальный минимум функции ошибки. В дальнейшем оказалось, что таким образом невозможно настроить крупные сети. Для решения этой проблемы был разработан «метод обратного распространения ошибки» (Каллан, 2001), реализованный в функции neuralnet(). Его смысл можно примерно изложить так. Предварительно задав случайные значения параметрам a_i, на выходе сети после расчетов получают ошибку S_i = Σ(y – ŷ)², которую используют для повторной корректировки значений параметров a_i+1 = f(–S_i, a_i). При этом перерасчет коэффициентов идет по слоям в обратном порядке, начиная с последнего и заканчивая первыми. Метод обратного распространения ошибки довольно медлителен. Так, для подбора коэффициентов простой линейной модели ему потребовалось 123 шага (рис. 11 А), тогда как функция алгоритма прямой подгонки nls(), решающая ту же задачу, справилась с ней за одну итерацию (рис. 5). Однако важнее всего то, что этот алгоритм позволяет выполнить настройку сетей любого размера и риск «застрять» в локальном минимуме функции ошибки при этом минимален (хотя такие случаи встречались даже в нашем примере).

 Сеть с одним слоем нейронов

В целом эффективность нейросети может существенно возрасти при осознанном подборе числа нейронов и слоев. Большую роль играет и направление связей (структура сети); об одной из таких конструкций, о рекуррентных сетях, можно прочесть в статье В. К. Шитикова (2023). Однако этот вопрос выходит за рамки нашего повествования.

Ниже будет рассмотрен многослойный персептрон. Для краткой записи структуры сети указывают число нейронов в каждом слое и соединяют их стрелками. Например, краткое обозначение сети с двумя ковариатами на входе, одним слоем из трех скрытых нейронов и с одной выходной переменной примет вид: 2→3→1 или 2>3>1.

Рассмотрим применение ИНС для решения распространенной задачи в зоологии ‒ определение пола особей по экстерьерным признакам. В примере требуется определить пол гадюк по замерам длины хвоста (lc), длины тела (lt), массы тела (w). По сравнению с одновозрастными самками у самцов хвост длиннее, хотя длина тела и масса меньше. Однако у разновозрастных животных распределения показателей имеют существенную трансгрессию по полам. К обучению сети привлечены данные по 50 разнополым разновозрастным взрослым особям гадюки (0 ‒ самки, 1 ‒ самцы), случайно извлеченным из общей базы данных (файл с данными vipkar.csv); для верификации модели взяли 50 других случайных особей.

Построили четыре модели (рис. 13). В первой модели (ns~lc) (1>1) (рис. 14 А) нейроны отсутствовали, полученная линейная регрессия позволяет успешно идентифицировать пол лишь у 83 % особей, а на проверочной выборке ‒ у 78 %.

Во вторую модель (ns~lc) (1>1>1) (рис. 14 Б) ввели лишь один нейрон. На диаграмме хорошо проявилась сущность отдельного нейрона – это логистическая регрессия, выраженная характерным s-образным графиком. Несмотря на многократные попытки, модель не смогла сформировать удовлетворительное правило половой диагностики (17 % ошибочных ответов на обучающей выборке и 22 % на проверочной).

 

library(neuralnet) library(neuralnet) v←read.csv( "vipmor.csv") head(v,3) n sex ns lc lt w 1 154 f 0 45 36 40 2 269 m 1 57 41 45 3 473 f 0 58 44 53 plot(v$lc,v$ns,ylim=c(-0.1,1.1)) nv←neuralnet(formula = ns~lc, data = v, hidden = 1) wn←(as.vector(nv$net.result[[1]])) points(v$lc,wn,pch=16) legend('left',legend=c(1:2),pch=c(1,16)) plot(nv) plot(v$ns,wn) abline(h=0.5,lty=2) sum(v$ns==round(wn,0))/nrow(v) [1] 0.8333333

Рис. 13. Расчеты для модели диагностики пола гадюк с одним нейроном

Fig. 13. Calculations for a model with one neuron to diagnose the sex of vipers

 

В конструкцию третьей модели включили все три изучаемые переменные (ns~lc+lt+w) (3>3>1) и внутренний слой, состоящий из трех нейронов (рис. 14 В). Запись функции имеет такой вид (вместо пятой строки скрипта на рис. 13):

nv←neuralnet(formula = ns~lc+lt+w, data = v, hidden = 3).

Настройка выполнялась несколько раз, пока не был получен лучший результат – правильная идентификация всех особей из обучающей выборки и 98 % – из проверочной.

В четвертом варианте в качестве выхода указали символьную переменную sex (sex~lc+lt+w) (3>3>2):

nv←neuralnet(formula = sex~lc+lt+w, data = v, hidden = 3).

Функция neuralnet() сама построила сеть с двумя выходными переменными (для самок и самцов, f и m), составленными из нулей и единиц, значения которых альтернативны (рис. 14 Г). Прогноз этой модели оказался столь же точен, как и для числовой выходной переменной.

 

  

 Рис. 14. Модели классификация гадюк по полу без нейрона (А), с одним нейроном (Б), с одним слоем из трех скрытых нейронов (В, Г): 1 ‒ исходные данные (v$ns), 2 ‒ модельная оценка пола (wn)

 Fig. 14. Models for classifying vipers by sex without a neuron (A), with one neuron (Б), with one layer of three hidden neurons (В, Г): 1 ‒ initial data (v$ns), 2 ‒ model assessment of sex (wn)

 

Возникает вопрос, почему в третьем и четвертом вариантах использовали слой именно из трех нейронов, а не из двух или десяти? Существуют ли какие-либо формальные критерии назначения числа нейронов в слое и числа слоев в модели? Нет, таких критериев нет. Важно только, чтобы модель хорошо описывала реальность. Как структурные характеристики (число слоев и нейронов в слоях ‒ их называют гиперпараметры), так и числовые коэффициенты (параметры a) должны подбираться эмпирически. В среде R возможна частичная автоматизация этой процедуры и оценка лучшего варианта расчетов с помощью пакета caret (Шитиков, Мастицкийй, 2017). Мы ограничились «ручным» перебором.

Здесь необходимо добавить, что отдельные нейроны одного слоя и целые слои могут получить содержательную интерпретацию. Если рассмотреть величину весовых коэффициентов, то можно заметить, что отдельные нейроны берут на себя большую или меньшую роль в определении того или иного типа исходов работы сети. Это может иметь значение для интерпретации сетей, особенно автоассоциативных.

 Нейросеть с несколькими скрытыми слоями

Рассмотрим пример постепенного усложнения композиции сети в стремлении добиться лучшего результата.

Поставлена задача определения возможности обитания обыкновенной гадюки на любом острове Кижского архипелага (Онежское озеро, Карелия). В основу анализа положены многолетние экологические исследования (Коросов, 2009). Для 24 островов площадью от 2 до 200 га получены оценки численности (vb) взрослых особей обыкновенной гадюки (маршрутные учеты, выверенные по расчетам абсолютной численности), численность (fr) взрослых особей двух видов лягушек (оценки по учету кладок). Эти значения были переведены в 5 категорий численности видов на острове: 1 – вид не встречен или обнаружены единичные особи, 2 – обитает устойчивая популяция из десятков особей, 3 – на острове обитают сотни особей, 4 – обитают тысячи особей. В среде ГИС по данным полевой съемки и дешифрирования космических снимков построены карты островов и для каждого определена площадь самого острова (s, га) и элементов ландшафта: лесов (fo), лугов (me), болот с лужами (bo) (файл с данными kizhsdat.csv). Луга важны для гадюк как места прогрева и зимовки (в каменных кучах), болота ‒ как места нереста лягушек, их основного корма (рис. 15). Зарастание лесом лугов и болот приводит к исчезновению местообитаний как для гадюк, так и для их кормовых объектов.

Представленные описания выполнены в период с 1994 по 2004 г., когда на регионе еще велась сельскохозяйственная деятельность и на островах был представлен весь спектр биотопов ‒ от сплошного леса до обширных сенокосных лугов и пашен. Таким образом, нейросетевая модель была призвана описать основные закономерности распространения гадюки на островах Кижского архипелага. В последующие 20 лет сельское хозяйство стремительно деградировало и острова на существенных площадях покрылись лесами, вытеснив луга и живущих на них гадюк. Перед сетью поставлена задача спрогнозировать возможные уровни численности гадюки на островах Кижского архипелага в 2022 г. С этой целью по космическим снимкам за 2022 г. были построены векторные карты островных биотопов (рис. 15) и рассчитаны их площади (fo, me, bo). 

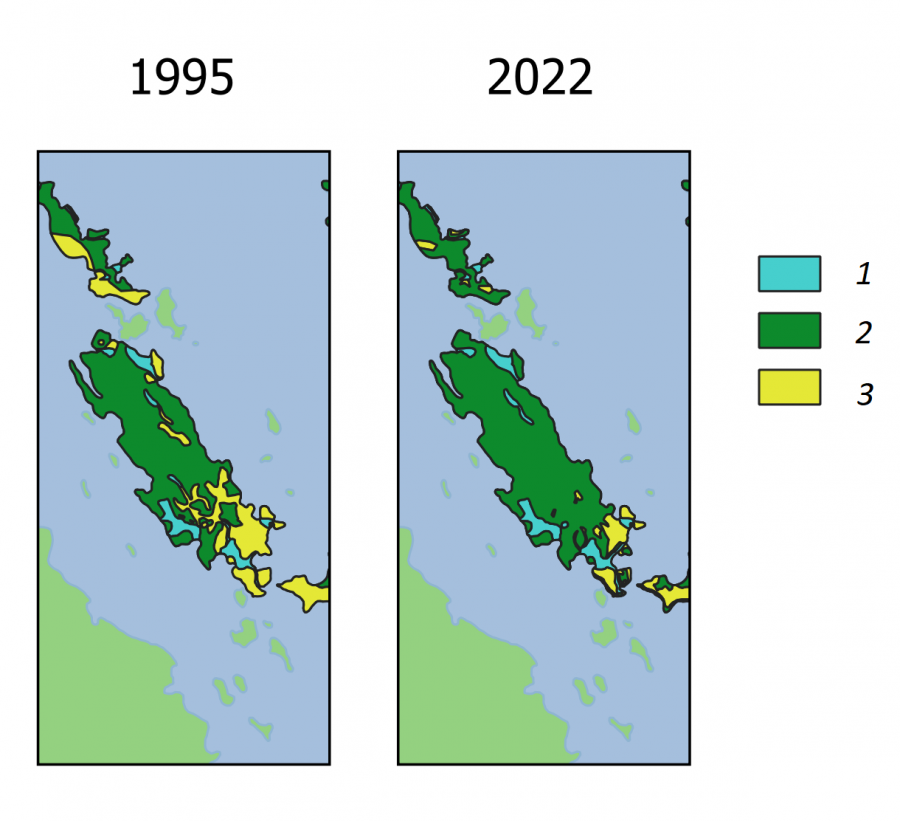
Рис. 15. Биотопы на о. Еглов в 1995 и 2022 гг.: 1 ‒ болота и лужи, 2 ‒ лес, 3 ‒ луга

 Fig. 15. Biotopes on the island Eglov in 1995 and 2022: 1 ‒ swamps and puddles, 2 ‒ forest, 3 ‒ meadows

 

Для настройки модели и ее проверки брали данные для 12 случайных островов (для 1995 г.). На листинге программы (рис. 16) представлен вариант настройки сети, давший 100 % совпадение для исходных данных и 83 % совпадение прогноза с проверочной выборкой. Сбой при проверке произошел относительно острова Мяль, для которого модель предсказала большую плотность поселения гадюки, чем была в реальности. На наш взгляд, главная причина состояла в том, что на острове практически отсутствуют каменные гряды, но этот фактор в модель не включали.

 

library(neuralnet) v←read.csv("kihzsdat.csv") head(v,3) name s fo me bo fr vb 1 mul 1.2 99 0 1 1 1 2 leb 1.2 99 0 1 1 1 3 gaj 1.6 90 9 1 1 1 nro←sample(1:24,12) ; d←v[nro,] nv←neuralnet(formula = vb ~ fo+me+bo, data = d, hidden = c(5)) nr←compute(x=nv, covariate=d)$net.result rnr←round(nr,0) data.frame(d$name,d$vb,rnr) d.name d.vb rnr 11 kar 1 1 12 ker 4 4 19 nol 3 3 22 ern 1 1 17 lel 1 1 14 syc 2 2 6 yab 1 1 8 kuy 1 1 15 dol 1 1 18 buk 3 3 13 lud 1 1 2 leb 1 1 sum(d$vb==rnr)/nrow(d) [1] 1 #----------------------- nro2←sample(1:24,12) ; d2←v[nro2,] nr2←compute(x=nv, covariate=d2)$net.result rnr2←round(nr2,0) data.frame(d2$name,d2$vb,rnr2) d2.name d2.vb rnr2 10 mal 1 4 13 lud 1 1 9 mak 1 0 22 ern 1 1 19 nol 3 3 4 sig 1 1 8 kuy 1 1 20 sol 3 3 6 yab 1 1 16 kal 1 1 17 lel 1 1 12 ker 4 4 sum(d2$vb==rnr2)/nrow(d) [1] 0.8333333

 Рис. 16.  Листинг обучения и проверки нейросети для классификации островов

Fig. 16. Listing of training and testing of a neural network for island classification 

 

Для иллюстрации характера влияния состава изучаемой выборки и структуры нейронной сети выполнили по 30 циклов настройка-проверка (каждый раз с новым составом выборок) для 8 вариантов сетей. Итоги настройки обобщили в виде средних значений доли правильных прогнозов и их дисперсии (табл. 1).

 

Таблица 1. Средние значения (M) и стандартное отклонение (S) доли правильных определений уровня численности гадюк на 12 случайных островах (по выборкам n = 30 повторностей) 

	Формула	Число нейронов в слоях	Выборки
			обучающая		проверочная
			M	S	M	S
1	vb ~ fo+me+bo	3>2>1	0.84	0.16	0.73	0.16
2	vb ~ fo+me+bo	3>6>1	0.97	0.08	0.75	0.12
3	vb ~ fo+me+bo	3>4>4>1	0.98	0.06	0.83	0.11
4	vb ~ fo+me+bo	3>6>6>6>1	0.98	0.06	0.81	0.08
5	vb ~ fo+me+bo+fr	4>6>1	0.95	0.10	0.74	0.13
6	vb ~ fo+me+bo+fr	4>6>6>1	0.98	0.08	0.75	0.12
7	vb ~ fo+me+bo+fr	4>6>6>6>1	0.96	0.09	0.80	0.12
8	vb ~ fo+me+bo+fr	4>30>30>1	1.00	0.00	0.79	0.12

 

Из таблицы видно: чем большое слоев имеет сеть и чем полнее исходные данные, тем выше величина совпадений прогнозов с обучающей выборкой, а их изменчивость снижается, т. е. перестает зависеть от случайных стартовых значений. Так, если для однослойной сети (3>2>1) совпадение прогноза с реальностью в разных прогонах варьировало от 0.53 (0.84 – 2*0.16) до 1 (0.84 + 2*0.16), то трехслойная сеть (3>6>6>6>1), построенная по неполным данным, давала прогнозы из более узкого диапазона 0.85–1.0, а сеть из 60 нейронов для полного списка ковариат (4>30>30>1) вообще не ошибалась на обучающих выборках (100 % правильных).

Вместе с тем заметен и другой эффект. Лучший средний прогноз на проверочной выборке дает достатоточно простая сеть 3>4>4>1 – 83 %, тогда как самая большая и, казалось бы, самая точная (5>30>30>1) ‒ лишь 79 %. Здесь проявился эффект «переобучения сети» – тренировка слишком большой сети или на слишком большом объеме обучающей выборки формирует сеть, которая очень хорошо распознает объекты в обучающей выборке, но плохо работает на других выборках. Понятно, что эффективная сеть должна одинаково хорошо распознавать объекты как обучающей, так и проверочной выборки, ведь главная цель сети – классифицировать объекты неизвестного статуса. Если выбирать из представленных моделей, то лучшей оказывается третья.

Нейронная сеть, построенная на материалах описания 24 островов в 1995 г., отражает основные закономерности распространения гадюки. Сеть использовали, чтобы рассчитать уровни численности гадюки (vb) на 28 островах в 1995 г.  и в 2022 г. по оценкам площадей таких же биотопов (fo, me, bo) (рис. 17, табл. 2).

 

 

head(d3←read.csv("squ island biotops 2022.csv"),3)      fo me  bo 1 57.9 4.1 3.4 2 35.3 0.0 7.9 3 83.0 7.3 11.5 nr3←compute(x=nv, covariate=d3)$net.result head(data.frame(d3$name,round(nr3,0)),3) d3.name rnr3 1      buk    2 2      dol    1 3      egl    1

Рис. 17. Листинг расчета уровня численности гадюки на островах в 2022 г.

Fig. 17. Listing of the calculation of the viper population level on the islands in 2022

 

Таблица 2. Оценки уровня численности гадюки на островах Кижского архипелага в 1995 и 2022 гг. 

	Название острова	1995	2022
1	Букольников	3	2
2	Долгий	1	1
3	Еглов	2	1
4	Ерницкий	1	1
	...
10	Кижи	4	4
11	Крестовский	1	1
	...
20	С. Олений	2	1
21	Рогачев	2	2
	...
27	Волкостров	4	2
28	Яблонь	2	1
	В среднем	2.0	1.6
	Численность, экз.	10533	4188

 

Как показали расчеты по модели, уровень численности на многих островах снизился, очевидно, за счет повсеместного лесовосстановления. Была рассчитана и средняя численности, исходя из следующих соотношений: уровень численности 1 примерно соответствует численности 3 экз., 2 ‒ 30 экз., 3 ‒ 300 экз., 4 ‒ 3000 экз. Расчеты показали, что за 30 лет численность гадюки на изученных островах упала приблизительно с 10000 до 4000 экз. Такого рода вывод может быть основой для планирования природоохранных мероприятий.

Заключение или выводы

Одно из центральных положений, рассмотренных в статье, состоит в том, что отдельный нейрон (с логистической функцией активации) по сути реализует логистическую регрессию, главная особенность которой ‒ преобразовывать непрерывное изменение входных переменных в скачкообразное (дискретное) изменение выходной переменной. Вместе с тем, объединив нейроны в сеть, мы получаем качественно новую конструкцию, со своими особенными свойствами и возможностями. В частности, на выходе многослойной сети можно получать градуально изменяющиеся величины.

Прогностические свойства нейронной сети определяются ее конструкцией. Обширная литература посвящена вариациям применения этого метода в зависимости от поставленных задач. Рассмотренный нами персептрон представляет собой сеть первого поколения. Современные сети третьего поколения (импульсная, сверточная, рекуррентная, гибридная) могут существенно расширить возможности для анализа экологических данных и прогноза экологических ситуаций.

Нейросетевое моделирование ‒ эффективный метод биометрии. Остается надеяться, что наша публикация упростит читателям освоение этой технологии.

Библиография

Благодарности

Автор признателен С. В. Бугмырину, Н. Д. Ганюшиной, В. В. Горбачу, В. К. Шитикову и рецензентам за разностороннее обсуждение рукописи и ценные замечания.