Введение
Современная теория экологических сообществ рассматривает модели биоразнообразия через призму набора базовых процессов, лежащих в основе появления и последующего развития каждого вида в конкретном местообитании (Vellend, 2016). Эти процессы определяются не только лимитирующими факторами среды, но и совокупностью собственных функциональных и морфологических характеристик каждого вида (traits), которые позволяют им адаптироваться к меняющимся условиям биотопа и занять свое место в сообществе с учетом всего комплекса эндогенных взаимодействий (Keddy, 1992; Fujinuma, Pärtel, 2023).
Если рассматривать видовой состав одного локального местообитания (участка или станции наблюдения) как одно сообщество, то совокупность всех таких местообитаний, объединенных определенными закономерностями распределения видового состава, можно назвать метасообществом (Leibold, Mikkelson, 2002). Матрица метасообщества B обычно состоит из участков (по строкам) и видов (по столбцам), встретившихся в изучаемом регионе, по крайней мере, один раз. Такая таблица может быть заполнена либо данными присутствия / отсутствия (1/0), либо численностью, либо проективным покрытием (например, в %). Очевидно, что эмпирическая видовая структура, основанная на натурных фаунистических исследованиях, подобна случайному моментальному снимку состава сообщества и не вполне соответствует истинному распределению регионального биоразнообразия. Для каждого местообитания можно выделить совокупность видов, которые теоретически по своим функциональным и аутэкологическим характеристикам могут принадлежать к рассматриваемому сообществу, но до некоторых пор не были там обнаружены. Подмножество таких видов было названо «темным» разнообразием (dark diversity) (Pärtel et al., 2011).
Существует целый ряд причин (Rabinowitz, 1981; Bickford et al., 2007; Klimesova, Klimes, 2007), почему некоторые виды могут отсутствовать на участках, подходящих им по совокупности абиотических или биотопических характеристик (или почему отдельные участки не могут включать все виды с подходящим набором свойств). В числе этих причин – недостаточное количество взятых проб, ошибки или тенденциозность в систематическом определении видов, их низкая способность к расселению или стрессоустойчивость и проч. И наоборот, инвазивные процессы, природно-климатические флуктуации и прочие случайные факторы могут привести к неожиданным разовым вспышкам численности видов, теоретически совершенно не характерных для конкретного сообщества.
Для объективной оценки видовой структуры локального сообщества необходимо создание аналитической схемы (метрик и моделей), позволяющей проводить формальную оценку истинного разнообразия. Последовательное продвижение в этом направлении осуществляется работами проф. Тартуского университета М. Партеля с соавторами (Pärtel et al., 2011, 2013). В своей недавней статье (Carmona, Pärtel, 2021) ими была разработана методика расчета матрицы S экологической пригодности (suitability) каждого вида для каждого участка, основанная на подсчете частот совместной встречаемости видов во всем метасообществе (т. е. в матрице B). Уникальные значения пригодности Sij (0 ≤ Sij ≤ 1) трактуются авторами как условные вероятности соответствия вида i и участка j.
В последующей публикации (Fujinuma, Pärtel, 2023) авторы предлагают новый унифицированный подход, который заполняет некоторую смысловую диспропорцию между биологическим понятием пригодности и формально-статистическими индексами на основе частот встречаемости за счет привлечения важнейших экологических закономерностей и факторов. При этом матрица Р условных вероятностей соответствия видов и участков формируется на основе произведения двух матриц: упомянутой выше S и D, связанной с экологическими особенностями, которые регулируются как биологическими свойствами видов, так и переменными абиотической среды, характерными для каждого участка. Байесовский подход позволил создать гибкую и сложную структуру модели для решения этой задачи.
Ранее (Головатюк и др., 2017, 2021) нами были рассмотрены особенности широтного и зонального градиентов распределения биоразнообразия видов донных сообществ равнинных рек в бассейне Средней и Нижней Волги. Цель настоящей статьи – на том же экспедиционном материале выполнить построение байесовской модели (Fujinuma, Pärtel, 2023) и оценить статистические возможности присутствия различных таксонов макрозообентоса на отдельных участках изученных водотоков. На основе анализа коэффициентов модели ставится также задача оценить эффекты влияния отдельных свойств видов и абиотических факторов на вероятности появления вида в конкретном сообществе.
Материалы
Анализ взаимосвязи таксономического состава донных сообществ с абиотическими условиями водной среды и экологическими характеристиками отдельных видов проводился по результатам многолетних (1990–2019 гг.) исследований на территории Среднего и Нижнего Поволжья (Зинченко, 2011; Головатюк и др., 2017, 2021). Гидробиологическую съемку макрозообентоса проводили в разные месяцы вегетационного периода на 90 малых и 12 средних равнинных реках, притоках Куйбышевского, Саратовского и Волгоградского водохранилищ, в т. ч. на 7 реках аридного региона бассейна оз. Эльтон. Средние реки были разделены на относительно однородные участки: верхнее, среднее, нижнее течение и устье, а каждая малая река принималась как целостный объект. Таким образом, было исследовано 132 локальных сообщества, в каждом из которых по стандартным методикам выделено до 40 видов макрозообентоса.
Всего было взято 1400 проб с идентификацией 740 видов и таксонов рангом выше вида, которые для дальнейшего статистического анализа были ограничены списком из 147 таксономических единиц, встретившихся не менее чем в 15 пробах или на 10 участках из 132. На основе данных о встречаемости этих видов формировалась исходная матрица B размерностью 132 × 147.
Матрицу T характеристик видов ограничили тремя количественными показателями (прологарифмированное значение среднего индивидуального веса, мг/экз., вычисленного по всем выполненным пробам; индекс сапробности в модификации Зелинки – Марвина; индекс экологичности донного грунта) и одной качественной переменной – тип питания, преимущественный для данного вида. Индексы сапробности для каждого вида рассчитывали по формуле:
Sr = (0⋅sx + 1⋅so + 2⋅sβ + 3⋅sα + 4⋅sp)/10,
где sx, so, sβ, sα, sp – сапробные валентности для ксеносапробной, олигосапробной, β-мезасапробной, α-мезасапробной и полисапробной зон соответственно. Индекс экологичности донного грунта рассчитывался по сходной методике: все грунты относились к 6 разрядам загрязненности (от 1 – песчано-гравийные до 6 – черный ил), вычислялись валентности, пропорциональные относительному частотному распределению встречаемости каждого вида в каждом типе грунта, после чего находился обобщенный показатель. Виды по типу питания были отнесены к 4 категориям: 1 – Фитофаги-собиратели, 2 – Хищники-хвататели, 3 – Детритофаги-собиратели, 4 – Сестонофаги-фильтраторы. Размерность матрицы T – 147 × 4, однако при построении модели каждая градация типа питания рассматривалась как отдельная переменная.
Матрица V условий внешней среды для каждого участка рек формировалась по данным параллельного мониторинга 30 показателей, включающих гидрологические параметры водотоков, индексы качества воды и содержание основных химических ингредиентов, а также растровых таблиц, содержащих основные метеорологические показатели для региона исследований, загруженных с сервера свободно распространяемой информации WorldClim. Поскольку между всеми этими переменными наблюдалась сильная корреляционная связь, проводили анализ индексов инфляции дисперсии VIF, и избыточные предикторы удалялись из рассмотрения. В результате было отобрано 7 факторов среды, коллинеарность которых оценивалась как приемлемая: среднегодовая температура, оС; осадки самого засушливого квартала, мм; высота, м; индекс шероховатости рельефа TRI; минерализация воды, мг/л; содержание аммонийного азота и кислорода O2, мг/л. На основе этих данных формировалась матрица V 132 × 7.
Перед построением модели все переменные матриц T и V стандартизировались с использованием среднего и стандартного отклонения.
Методы
Унифицированная байесовская модель «виды – участки» состоит из 3 последовательных операционных секций:
1. Оценка двух векторов dsp и dsite, состоящих из значений вероятности индивидуального сродства (affinity) для каждого вида i или участка j в отдельности (i = 1…147, j = 1…132) с помощью двух подмоделей логистической регрессии:
logit(dsp-i) = asp + bsp-i × Ti. и logit(dsite-j) = asite + bsite-j × Vj., (1)
где logit() – процедура логит-преобразования; asp и asite – свободные члены двух субмоделей; bsp-i = {b1,sp-i, b2,s-ip, …, b7,sp-i} и bsite-j = {b1,site-j, b2,site-j, …, b7,site-j} – векторы коэффициентов регрессии для соответствующих строк матриц биологических признаков Ti. применительно к виду i и факторов среды Vj. для участка j.
2. С использованием всех возможных линейных комбинаций значений векторов dsp и dsite рассчитывается обобщенная матрица D экологического сродства между каждым видом i и участком j:
logit(Di,j) = [logit(dsp-i) + logit(dsite-j)]/2. (2)
3. Осуществляется минимизация остатков модели (т. е. различий между матрицей B и прогнозом P) путем подгонки оценок модельных параметров {a, b}, описанных для первой секции 1. При этом предполагается, что наблюдаемая видовая структура метасообщества, описанная матрицей B, может быть аппроксимирована распределением Бернулли с матрицей вероятностей присутствия P, B ~ Bern(P), оценки которых (Pi, j) могут быть получены как скорректированная (унифицированная) пригодность вида i для конкретного участка j следующим образом
logit(Pi, j) = logit([1 – Di, j] × Si, j) + δ, (3)
где δ – постоянный параметр, уникальный для каждого метасообщества, Si, j – пригодность каждого из видов для конкретного участка, основанная на предположении, что часто совместно встречающиеся виды имеют общие экологические требования. Для оценки матрицы пригодности S по матрице присутствия / отсутствия видов B использовался R-пакет DarkDiv, рассчитывающий стандартизованное отклонение эмпирических частот от нуль-ожидаемых частот гипергеометрического распределения (Carmona, Pärtel, 2021).
Расчеты выполнялись с использованием языка и статистической среды R вер. 3.6. За основу был взят скрипт обработки тестового комплекта исходных данных, который представлен в приложении к статье (Fujinuma, Pärtel, 2023). Подгонка байесовской модели осуществлялась на основе итеративного процесса выбора исходных (априорных) оценок параметров модели и получении их результирующего (апостериорного) распределения. Этот процесс реализовали с использованием библиотеки JAGS методом построения длинных итеративных последовательностей нескольких марковских цепей Монте-Карло (MCMC), для которых распределение переходов определялось описанной выше структурой модели.
Результаты
Апостериорное распределение коэффициентов модели было получено с использованием марковского процесса из 2000 итераций для 3 цепей Монте-Карло (продолжительность вычислений – около 10 часов). Формальная проверка сходимости цепей осуществлялась с использованием статистики Гельмана – Рубина Rhat = 1.66, что соответствует не вполне хорошему результату (в этом случае статистика близка к 1).
Наиболее важное значение для предметной интерпретации имеют коэффициенты двух моделей логистической регрессии (1) bt.sp-i и bv.site-j для каждого t-го свойства i-го вида и каждой v-й абиотической переменной на j-м участке соответственно. В этих моделях положительные значения коэффициентов b приводят к возрастанию индивидуальных значений сродства с увеличением числовых независимых переменных, соответственно, возрастает шанс отсутствия i-го вида на участке j. Апостериорные плотности распределения, представленные на рис. 1, дают возможность заключить, что малозначимыми являются климатические факторы (температура воздуха и осадки); никак не влияют на встречаемость такие типы питания видов, как фитофаги и детритофаги, поскольку значительная часть распределения их коэффициентов близка к 0. Очевидно также, что при прочих равных условиях соленость воды и содержание ионов аммония снижают вероятность появления видов, тогда как насыщение кислородом, наоборот, увеличивает. Труднее распространяться видам с большой массой тела и детритофагам (в отличие от хищников). Не столь понятна связь встречаемости с качеством донных отложений и сапробностью, но можно высказать предположение, что видам, привыкшим к тяжелым грунтам и полисапробности, стратегически легче освоиться в менее экстремальных условиях.
А. Абиотические переменные по участкам [Abiotic variables by site]

Б. Свойства видов количественные [The properties of species are quantitative]

В. Трофические группы видов [Trophic groups of species]

Рис. 1. Апостериорные распределения коэффициентов логистической регрессии bsp и bsite
Fig. 1. Aposterior distributions of logistic regression coefficients bsp and bsite
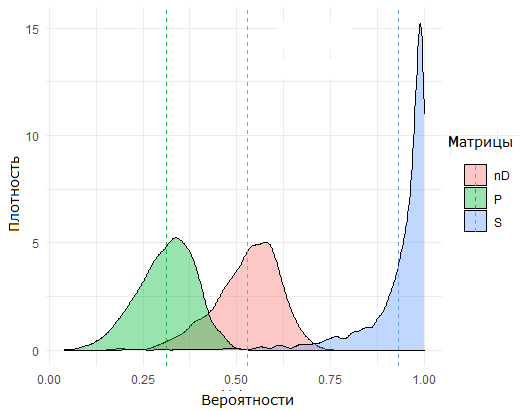
С использованием математических ожиданий коэффициентов b по формуле (2) была рассчитана матрица D экологического сродства (affinity), учитывающая биологические особенности видов и абиотические характеристики участков, а на основе анализа частот совместной встречаемости видов оценена матрица S пригодности (suitability). В результате их объединения по формуле (3) формировалась матрица P унифицированной (или приведенной) пригодности, отражающая в комплексе взаимные отношения видов и участков. Сравнение распределения значений этих трех матриц размерностью 132 × 147 для двух ситуаций (подмножеств клеток таблиц) с присутствием или отсутствием вида на участке (Вi,j = 1/0) представлено на рис. 2.
А. Для ячеек с встретившимися видами (Вi,j = 1) [For cells with encountered species]
Б. Для ячеек, где виды не встретились (Вi,j = 0) [For cells where species did not meet]
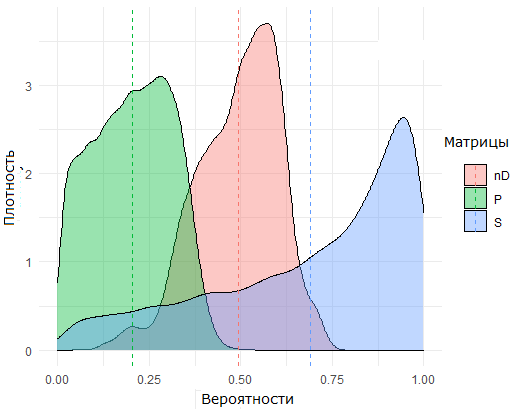
Рис. 2. Плотность распределения значений матриц пригодности S , сродства nD = (1 – D) и P унифицированной (или приведенной) пригодности; пунктиром обозначены центры (средние) каждого распределения
Fig. 2. The density of the distribution of the values of suitability matrices S, affinity nD = (1 – D) and P of unified (or reduced) suitability; dotted lines indicate the centres (averages) of each distribution
Обсуждение
Отнесение i-го вида к j-му участку и декомпозиция видового разнообразия на компоненты может проводиться с использованием любой из перечисленных матриц вероятности на основании известных методов классификации. Если, например, между центрами распределений матрицы S на рис. 2А и 2Б выбрать произвольное пороговое значение С (threshold), то виды считаются присутствующими при Pi, j > С или отсутствующими в противном случае. Тогда на каждом участке можно выделить 4 подмножества видов: «истинное разнообразие» TP (true positive), когда прогноз S совпадает с фактическим наблюдением в матрице B, «темное разнообразие» FP (false positive), «серое разнообразие» FN (false negative), когда модель признает обнаруженный вид маловероятным, и солидарно отсутствующие виды TN (true negative).
Общепринятым графоаналитическим методом нахождения наилучшего решения является ROC-анализ (от Receiver Operator Characteristic), в ходе которого находится оптимальный баланс между максимальным охватом positive случаев, т. е. чувствительностью TP / (TP + FN) = 0.771, и минимизацией неправильной классификации negative случаев, т. е. специфичностью FP / (FP + TN) = 0.74 (рис. 3). Пороговое значение С = 0.912 пригодности Si, j выбирается с учетом максимума суммы чувствительности и специфичности. В качестве критерия оценки качества приближения матриц S и B используется площадь под ROC-кривой (Area Under Curve) AUC = 0.832.
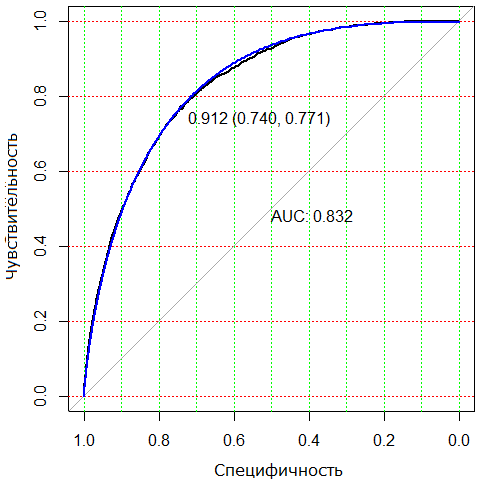
Рис. 3. ROC-диаграмма для предсказания присутствия видов на участках по матрице вероятностей пригодности S. Показаны достигнутый критерий AUC, пороговое значение С и (в скобках) величины специфичности и чувствительности соответственно
Fig. 3. ROC diagram for predicting the presence of species in plots based on the unified probability matrix S of suitability. The achieved AUC criterion, threshold value c and (in parentheses) the values of specificity and sensitivity, respectively, are shown
Отметим, что выполнить подобную операцию с матрицами сродства D и унифицированной матрицей пригодности Р было бы некорректно по двум причинам: a) применение операции logit() в формулах (1–3) автоматически приводит к порогу классификации t = 0.5; б) применение байесовской процедуры для оценки коэффициентов логистических уравнений (1) настроено на оптимизацию темного разнообразия, а не на общую ошибку распознавания.
В качестве примера приведем анализ видового состава типичной малой реки Тукшумка, имеющий умеренный уровень стресса со стороны факторов среды (dsite = 0.438). По результатам двух гидробиологических проб было обнаружено 19 видов и еще 16 видов было отобрано в качестве потенциального видового богатства, которое, вероятнее всего, будет выявлено при повторных отборах проб. Фрагменты этих двух таксономических списков представлены в таблице.
Наблюдаемое и потенциальное видовое богатство р. Тукшумка, полученные на основе трех оценок вероятности: пригодности S, сродства для видов dsp, общего сродства D и унифицированной пригодности Р
| Наименования видов | S | dsp | D | P |
| Наблюдаемое разнообразие | ||||
| Polypedilum scalaenum | 0.995 | 0.474 | 0.456 | 0.541 |
| Limnodrilus profundicola | 0.904 | 0.380 | 0.408 | 0.535 |
| Cricotopus sp. | 0.952 | 0.445 | 0.441 | 0.532 |
| Tanytarsus sp. | 0.961 | 0.473 | 0.455 | 0.523 |
| Prodiamesa olivacea | 1.000 | 0.535 | 0.486 | 0.514 |
| Paracladius conversus | 1.000 | 0.552 | 0.495 | 0.505 |
| … | ||||
| Темное разнообразие | ||||
| Stylaria lacustris | 0.937 | 0.291 | 0.361 | 0.599 |
| Limnodrilus sp. | 0.947 | 0.313 | 0.373 | 0.593 |
| Uncinais uncinata | 0.942 | 0.309 | 0.371 | 0.592 |
| Harnischia curtilamellatus | 0.959 | 0.370 | 0.403 | 0.572 |
| Potamothrix hammoniensis | 0.963 | 0.386 | 0.412 | 0.566 |
| Thienemannimyia sp. | 0.996 | 0.456 | 0.447 | 0.551 |
| Paratendipes albimanus | 0.965 | 0.475 | 0.456 | 0.525 |
| Nais communis | 0.845 | 0.324 | 0.379 | 0.525 |
| Paracladopelma сamptolabis | 0.983 | 0.500 | 0.468 | 0.522 |
| Stempellina almi | 0.940 | 0.459 | 0.448 | 0.519 |
| Polypedilum convictum | 0.970 | 0.497 | 0.467 | 0.517 |
| Paralauterborniella nigrohalteralis | 0.905 | 0.436 | 0.437 | 0.510 |
| Harnischia fuscimana | 0.910 | 0.445 | 0.442 | 0.508 |
| Sialis sp. | 0.939 | 0.483 | 0.460 | 0.507 |
| Paratanytarsus lauterborni | 0.879 | 0.410 | 0.424 | 0.507 |
| Clinotanypus nervosus | 0.838 | 0.368 | 0.402 | 0.501 |
Заключение
Построение вероятностных моделей формирования видового состава становится важным инструментом при проведении экологических и биогеографических исследований. На региональном уровне эти модели связывают биоразнообразие локальных участков с пулом видов всего метасообщества, что позволяет объяснить экологические механизмы эволюции лотических сообществ, композиционные сдвиги и потоки распространения биоты в пространстве. Исследования с привлечением модельных коэффициентов позволяют понять особенности функциональной экологии: например, как биологические свойства видов (такие как средний размер или индивидуальная масса, форма тела, продолжительность жизни, количество генераций, подвижность личинок и их участие в дрифте, тип и способ питания, суточные изменения активности и др.) в сочетании с абиотическими характеристиками биотопов сказываются на реализации потенциального видового разнообразия в той или иной местности. Изучение состава видов, с высокой вероятностью включенных в темное разнообразие, может быть полезно при определении приоритетов охраны природы: среди них могут оказаться либо исчезающие виды, нуждающиеся в сохранении, либо чужеродные виды, к будущим вторжениям которых следует своевременно подготовиться.
В то же время оценки вероятности Pij обнаружить i-й вид на j-м участке не сводятся только к биологическим свойствам видов dsp, абиотическим факторам dsite и частотам совместной встречаемости S. В большинстве случаев реализуемый план исследований связан с пространственными координатами, и тогда состав видов темного разнообразия обусловлен пространственной автокорреляцией (видовое богатство на участках, расположенных близко друг к другу, вероятнее всего, будет более сходными, чем для выборочных точек, расположенных далеко друг от друга). Кроме того, на таксономическом дереве можно выделить группы видов с высокой филогенетической корреляцией. В локальное сообщество для выполнения определенной экологической роли обычно входит только часть видов каждой группы и один вид постоянно сменяет другой, выполняя ту же функцию. То есть на оценку темного разнообразия может влиять филогенетический сигнал. В связи с этим современные многомерные модели совместного пространственного распределения видов (Ovaskainen, Abrego, 2020; Шитиков и др., 2021) дополнительно учитывают филогенетическую структуру сообществ и пространственную автокорреляцию данных в точках наблюдений.
Библиография
Головатюк Л. В., Зинченко Т. Д., Шитиков В. К. Пространственное распределение разнообразия донных сообществ лотических систем Среднего и Нижнего Поволжья // Принципы экологии. 2021. № 2. С. 38–53. DOI: 10.15393/j1.art.2021.11122
Головатюк Л. В., Шитиков В. К., Зинченко Т. Д. Оценка зонального распределения видов донных сообществ равнинных рек бассейна Средней и Нижней Волги // Поволжский экологический журнал. 2017. № 4. C. 335–345.
Зинченко Т. Д. Эколого-фаунистическая характеристика хирономид (Diptera, Chironomidae) малых рек бассейна Средней и Нижней Волги (Атлас) . Тольятти: Кассандра, 2011. 258 с. URL: http://www.ievbras.ru/books/books.html (дата обращения: 01.06.2023).
Шитиков В. К., Зинченко Т. Д., Головатюк Л. В. Модели совместного распределения видов на примере донных сообществ малых рек Волжского бассейна // Журнал общей биологии. 2021. Т. 82, № 2. С. 143–154.
Bickford D., Lohman D. J., Sodhi N. S., Ng P. K. L., Meier R., Winker K., Ingram K. K., Das I. Cryptic species as a window on diversity and conservation // Trends Ecol Evol. 2007. Vol. 22, № 3. P. 148–155. DOI: 10.1016/j.tree.2006.11.004
Carmona C. P., Pärtel M. Estimating probabilistic site-specific species pools and dark diversity from coocurrence data // Global Ecology and Biogeography. 2021. Vol. 30, № 1. P. 316–326. DOI: 10.1111/geb.13203
Fujinuma J., Pärtel M. Decomposing dark diversity affinities of species and sites using Bayesian method: What accounts for absences of species at suitable sites? // Methods in Ecology and Evolution. 2023. P. 1–12. DOI: 10.1111/2041-210X.14109
Keddy P. A. A pragmatic approach to functional ecology // Functional Ecology. 1992. Vol. 6. P. 621–626.
Klimesova J., Klimes L. Bud banks and their role in vegetative regeneration – a literature review and proposal for simple classification and assessment // Perspectives in Plant Ecology, Evolution and Systematics. 2007. Vol. 8. P. 115–129.
Leibold M. A., Mikkelson G. M. Coherence, species turnover, and boundary clumping: elements of meta-community structure // Oikos. 2002. Vol. 97. P. 237–250.
Ovaskainen O., Abrego N. Species Distribution Modelling: With Applications in R. Cambridge: Cambridge Univ. Press, 2020. 370 p.
Pärtel M., Szava-Kovats R., Zobel M. Community completeness: linking local and dark diversity within the species pool concept // Folia Geobotanica. 2013. Vol. 48, № 3. P. 307–317. DOI: 10.1007/s12224-013-9169-x
Pärtel M., Szava-Kovats R., Zobel M. Dark diversity: shedding light on absent species // Trends in Ecology and Evolution. 2011. Vol. 26. P. 124–128.
Rabinowitz D. Seven forms of rarity // The biological aspects of rare plant conservation. New York: John Wiley & Sons Ltd, 1981. P. 205–217.
Vellend M. The Theory of Ecological Communities. Princeton; Oxford: Princeton Univ. Press, 2016. 229 p. .
Благодарности
Авторы выражают признательность д. б. н. Л. В. Головатюк за активное участие в сборе гидробиологического материала и определении видов, а также проф. М. Партелю и Г. Фуджинума (Тартуский университет) за ценные замечания при обсуждении рукописи.






 © 2011 - 2026
© 2011 - 2026