Введение
Современные научные представления (модели) о живой форме стандартной материи включают понятия, сформулированные ранее в процессе изучения неживой формы той же стандартной материи. Целесообразность применимости тех или иных «физических» моделей к биологическим объектам или к любым объектам и процессам, в которых прямо или косвенно принимает участие живое вещество, определяется прагматическими возможностями обобщения разнообразных исходных данных, получения прогноза эволюции исследуемых объектов и формулировки системы критериев выделения и сравнительной оценки их состояний. Экстремальная сложность структуры и функционирования живой материй, ощущаемая биологами, вызывает психологическое отторжение «простых» физических моделей. Во второй половине XX в. физики (Э. Шрёдингер), а затем кибернетики (У. Р. Эшби, Х. Фёрстер, Л. фон Берталанфи) предлагали «глобальные» решения проблемы эволюции жизни и человеческого сознания. Эти модели оказали существенное влияние на развитие отдельных направлений научной мысли внутри биологии и современной информационной технологии в целом, но не стали основой для общей теории эволюции, которой не существует и в настоящее время. Показательно, что С. Хокинг (Hawking, 2002) в курсе лекций «Теория всего. Происхождение и судьба Вселенной» избегает тематики эволюции жизни, а Э. Майр в одной из последних работ «What evolution is?» (Mayr, 2001) выражает сомнение в том, что законы физики способны объяснить биологическую эволюцию.
Биологические объекты относятся к особому классу физических систем, которые характеризуются как открытые, находящиеся далеко от состояния термодинамического равновесия, демонстрируют нелинейную динамику с резкими изменениями значений параметров, обладают способностью одновременно и к самоорганизации, и к эволюции. Большинство физических моделей имеют явные «решения» для систем в состоянии равновесия или в области стационарной динамики (без изменения величин параметров системы). Детерминистская идея нового времени (XVI–XIX вв.) о том, что знание «законов природы» дает возможность делать точный прогноз ее эволюции, оказалась неверной в отношении даже физических в узком смысле, но нелинейных систем с высокой чувствительностью к начальным условиям и с высоким вкладом стохастической и нестационарной компонент в их динамике (Майнцер, 2009).
Мы полагаем аксиоматически (Пузаченко, 2016), что возникновение и эволюция живого вещества на Земле является частью более общего явления – эволюции стандартной материи. Максимальный уровень сложности организации и функционирования достигается на уровне живой формы материи. Способность именно стандартной материи к формированию сложных систем обусловлена разнообразием (максимально возможным?) типов физических взаимодействий, которые при определенных условиях возникают между состоящими из нее материальными системами. В этом и заключается ее принципиальное отличие от любых других форм материи.
Существует преемственность ограничений, возникших эволюционно, между последовательными стадиями эволюции сложности материальных систем. Совокупность этих ограничений составляет «память» материальных систем. Преемственность ограничений подразумевает возможность передачи сохраненной информации между системами, в том числе разного уровня сложности.
Вне зависимости от «физической природы» и иерархического уровня сложности систем, изменение их состояния в результате взаимодействий сопровождаются синтезом – передачей – приемом энтропии-информации.
В основе эволюции лежат процессы, имеющие стохастическую природу. Поэтому эволюция в целом не может адекватно интерпретироваться как телеономический процесс. В процессе эволюции область всевозможных реализаций стохастических процессов ограничена, с одной стороны, значениями физических параметров среды, а с другой – «памятью» системы. По этой причине для внешнего наблюдателя эволюционный процесс выглядит целенаправленным, детерминированным.
В данной работе мы показываем наличие фундаментальных (физических) ограничений процесса самоорганизации в сложных системах, которые являются следствием закона Шеннона – Хартли о пропускной способности информационного канала с шумом.
Материалы
Исследованы 7507 черепов взрослых экземпляров 35 видов, относящихся к 14 семействам четырех отрядов млекопитающих – Artiodactyla, Carnivora, Perissodactyla и Rodentia. Данные по элементам посткраниального скелета (кости плюсны, пясти и таранная кость) включают измерения 3830 костей, принадлежащих пещерным медведям (Ursus deningeri, U. spelaeus, U. kudarensis) и кабаллоидным лошадям (плейстоценовые Equus ferus и современные E. f. przewalsskii). Материал для исследования постнатального онтогенеза включал: 493 черепа бобра (Castor fiber) и 261 череп обыкновенного слепыша (Spalax microphthalmus).
Методы
Базовые сведения о формальной основе развиваемой нами общей модели приведены в (Пузаченко, 2000, 2001, 2011, 2013, 2016; Puzachenko, Markova, 2011; Abramov, Puzachenko, 2012; Puzachenko, Korablev, 2014). Теоретические основания для модели мы находим в основном в результатах математической теории связи по К. Шеннону и кибернетике. В последнем случае особое значение имеет теория, изложенная в ряде работ У. Р. Эшби (Ashby, 1947, 1962).
Содержание понятия информации/энтропии в отношении биологических систем по-разному интерпретируется в зависимости от методологии научного исследования, его задачи и особенностей объекта исследования (Atlan, 1977; Пузаченко Ю., 1992, 2009; Schneider, 2000; McCowan et al., 2002; Collier, 2008; Puzachenko J., 2008; Tkačik, Bialek, 2016). Рассматривать информацию как особую физическую переменную впервые предложил Н. Винер (Винер, 1983). Л. Бриллюэн (1960) с учетом общих математических свойств и ограничений приравнял информацию к отрицательной энтропии (Schrödinger, 2012), назвал ее «негэнтропией» и предложил измерять ее в одних и тех же физических единицах. Для целей настоящей работы будет наиболее приемлемым подход к определению информации, который независим (инвариантен) от конкретных особенностей объекта исследования. Ю. Г. Пузаченко рассматривал информацию как «отображение, преобразование одних структур в другие, как взаимоограничение взаимодействующих явлений и событий» (Пузаченко Ю., 1992, с. 13). Эта трактовка, будучи содержательно шире, соответствует понятию информации в «узком смысле» в теории передачи сигналов или теории информации K. Шеннона (Shannon, 1948, 1949; Shannon, Weaver, 1949).
Процессы самоорганизации биологических систем, имеющие результатом как усложнение, так и упрощение структуры систем, реализуются на любом уровне организации стандартной материи и не являются исключительным атрибутом живого вещества. По Х. Фёрстеру (Foerster, 1960), эти части большой системы должны потреблять энергию и порядок из окружающей среды. В качестве среды может выступать другая подсистема (другие подсистемы) внутри системы или другая система (другие системы). Третьим важным условием является неоднородность самой среды.
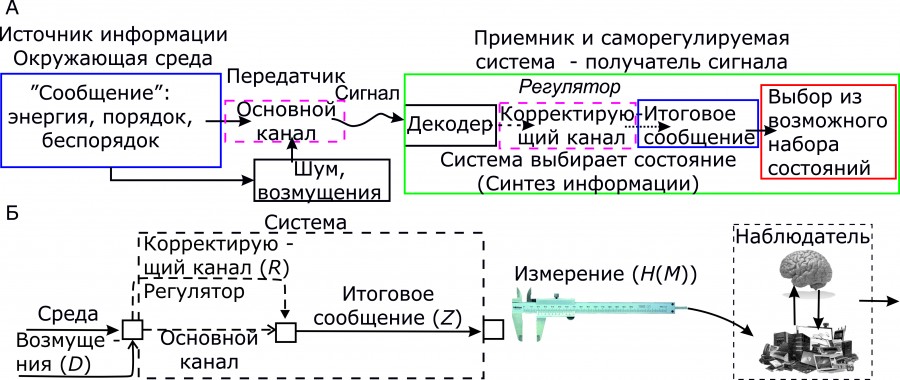
Рис. 1. Схема информационных каналов между «средой» и «системой» (приемник). A – обобщенная схема информационных потоков; Б – кибернетическая интерпретация информационных потоков и «измерений» объекта, производимых наблюдателем: H(Z), H(D), H(R), H(M) – энтропии объекта (измеряемых переменных), среды, регулятора, измерений и энтропия ошибок измерения (H(ошибки)) соответственно; H(Z) ≥ H(D) – H(R), H(M) = H(Z) + H(ошибки)
Fig. 1. The scheme of information channels between the “environment” and the “system” (receiver). A – generalized scheme of information flows; Б – cybernetic interpretation of information flows and “measurements” of an object made by an observer: H(Z), H(D), H(R), H(M), is the entropy of an object (measured variables), environment, controller, measurements and entropy of measurement errors (H(errors)), respectively; H(Z) ≥ H(D) – H(R), H(M) = H(Z) + H(errors)
Как показано на рис. 1A, основной канал связи может быть частью «среды» относительно системы – приемника «сообщения». В самоорганизующихся и не только системах сигнал обрабатывается (декодируется) в форму сигнала, который может интерпретироваться в качестве семантической информации (порядка) для изменения (выбора из возможного множества) того или иного ее состояния.
Проблема подавления шума или исправление ошибок в системе возникает не только в процессе самоорганизации, но и при поддержании стационарного состояния, т. е. поддержания достигнутого уровня порядка (гомеостаз). Подсистема, обеспечивающая поддержание гомеостатического (стационарного) состояния системы, в кибернетике обозначается понятием «регулятор». Регулятор – это абстрактный преобразователь информации в общем случае неизвестной природы, влияющий в конечном итоге на выбор системой того или иного состояния. Регулятор формирует свой информационный канал, который на рис. 1A обозначен как «корректирующий». В соответствии с теорией, поддержание стационарных значений переменных системы происходит как противодействие внешним или внутренним возмущениям и возможно исключительно за счет роста внутреннего разнообразия (энтропии, сложности организации) самого регулятора (закон необходимого разнообразия – requisite variety (Ashby, 1956)).
Если известна величина энтропии-информации (H), синтезируемая системой, то на ее основе можно получить оценку «избыточности» сообщения (redundancy, R), или «вырожденности кода» сообщения (Shanon, 1948): R = 1 – H/Hmax = 1 – [(–∑pilog2pi)/(–log2N)], где H – энтропия системы, pi – оценка вероятности i-го состояния системы, Hmax – максимальная энтропия. Максимальная энтропия пропорциональна логарифму числа элементов системы (Foerster, 1960): N (Hmax = C1 + C2log2N), где C1 и C2 – константы. Отношение энтропии к ее теоретическому максимуму К. Шеннон назвал «относительной энтропией» (Shanon, 1948).
Согласно модели Х. Фёрстера (Foerster, 1960), в самоорганизующейся системе происходит рост R, что соответствует положительности производной R по времени. Поэтому R можно интерпретировать и как меру внутренней упорядоченности или организованности системы.
Пропускная способность информационного канала – важнейшая характеристика, которая не зависит от природы канала и природы самого сигнала. Г. Т. Найквист установил (Nyquist, 1924, 1928), что число независимых импульсов («точек» и «тире») в единицу времени, которые могут быть переданы через телеграфный канал без ошибок, ограничено удвоенной максимальной частотой дискретизации непрерывного сигнала. Практически одновременно Р. Хартли (Hartley, 1928) ввел меру информации, передаваемой по каналу с помощь электрических импульсов разной мощности (~ амплитуды), которая пропорциональна мощности импульса источника сигнала и обратно пропорциональна точности, с которой приемник может различать сигналы разной мощности. Но наиболее общий подход в этой области теории был предложен К. Шенноном (Shannon, 1949). Он определил скорость передачи M сигналов за время T (M/T) как log2M/T. Максимальное (предельное) количество сигналов при T, стремящихся к бесконечности, он обозначил как емкость или пропускную способность информационного канала (channel capacity): C = lim(log2M/T) (T->∞).
К. Шеннон связал величину С с полосой частот сигнала, мощностью сигнала и шумом в информационном канале. Пропускная способность прямо пропорциональна ширине полосы частот (W = ∑wi) передачи сигналов и логарифму отношения мощности сигнала (P = 1/2TW) к мощности шума (N): C = Wlog2K2(1 + P/N) = Wlog2K2[1 + P/(N0W)], где N0 – удельная мощность теплового («белого», гаусcовского) шума на единицу полосы частот (1 Гц), а K – небольшая близкая к 1 константа, зависящая от требуемого качества передачи сигнала.
При увеличении/сокращении полосы частот W пропорционально возрастает/снижается мощность теплого шума: N = N0W. Введя обозначение W0 = P/N0 для частоты, при которой мощность сигнала (P) равна мощности теплового шума (N0), и приравнивая K к 1, выражение для пропускной способности можно переписать в виде (Shannon, 1949): C/Wo = W/Wolog2(1 + Wo/W). По мере увеличения полосы частот W от 0 до 1 пропускная способность быстро увеличивается до того момента, когда мощность шума становится равной мощности сигнала (W/W0 = 1), где С = 1. После этого, несмотря на увеличение полосы частот, прирост пропускной способности снижается. С ростом W величина C приближается к асимптотическому значению log2e ≈ 1.443.
Необходимо отметить и ограничения в приложении рассмотренной модели для реальных объектов, явлений и их моделей – систем. Область определения модели К. Шеннона ограничена эргодическими процессами. Другими словами, предполагается, что передача сигнала – процесс как минимум стационарный. На описание передачи сигнала для сильно неравновесных нелинейных процессов эта модель не распространяется (Ashby, 1958). Однако в большинстве случаев и большую часть своей жизни наблюдаемые нами сложные системы находятся в стационарных состояниях. Поэтому ограничения, связанные с законом Шеннона – Хартли, распространяются на подавляющее большинство случаев, но не на неравновесные переходы от одного стационарного состояния к другому стационарному состоянию.
Согласно У. Р. Эшби (Ashby, 1956, 1958), «разнообразие» (variety) в кибернетике имеет значение числа различимых элементов некоторого множества или логарифм этого числа, например, по основанию 2. Из этого прямо следует, что кибернетическое разнообразие соответствует энтропии/информации в теории информации. У. Р. Эшби вывел базовые ограничения возможных способов управления и организации сложных систем, ввел понятие «существенных переменных» (essential variables) как фундаментальных переменных, значения которых должны поддерживаться в определенных «физиологически» допустимых границах, обеспечивающих выживание системы (устойчивость, гомеостаз). Последнее в этой модели рассматривается как цель регуляции. Эта цель определяет параметры работы и внутреннее разнообразие гипотетического «регулятора» (см. рис. 1A).
В общем случае содержание понятия регулятора (= абстрактный преобразователь информации) соответствует модели саморегуляции на уровне выделенной системы и в этом смысле является моделью самой системы (Conant, Ashby, 1970). Регулятор должен управлять дисперсией сигналов, исходящих из «среды», которая пропорциональна величине энтропии/информации. Возмущения (disturbances), которые поступают в систему из среды, образуют множество, которое может быть распознано регулятором. С одной стороны, физическое и биофизическое (на Земле) разнообразие внешней среды огромно. С другой стороны, большинство потенциальных сигналов среды не влияют на существенные переменные системы. Поэтому в существовании универсального регулятора, «на все случаи жизни» нет необходимости, но нет и теоретической возможности для его осуществления. Сложность самого регулятора должна находиться в соответствии со сложностью, образно говоря, сигнального поля среды, имеющего значение для существования системы. Другими словами, регулятор может достичь своей цели исключительно за счет увеличения своего внутреннего разнообразия (энтропии) или сложности (Ashby, 1956).
Закон необходимого разнообразия регулятора в терминах теории информации утверждает, что способность регулятора ограничена его пропускной способностью, как если бы он представлял из себя (в модели системы) информационный канал (Ashby, 1958). Это определяет и ограничение возможностей регулирования, и варианты улучшения регулирования в случае роста энтропии/информации в среде.
Пропускная способность изучаемой системы может быть записана как линейная функция от ее меры организованности: C = (1 – R)log2e. Величина R в точке перегиба графика (W/w0 = 1, С/w0 = 1) равна: R = 1 – H/Hmax = 1 – 1/log2e ≈ 1 – 0.693 = 0.307.
Эффективность работы канала передачи информации (ЄR) прямо пропорциональна его пропускной способности (C) и обратно пропорциональна отношению мощностей сигнала и шума: R = C/PN-1.
Наблюдатель/исследователь, проводящий измерения и анализ данных (в самом широком понимании содержания понятий «измерение» и «анализ»), может быть «встроен» в информационную систему «среда – система – наблюдатель», как это показано на рис. 1Б. Если у наблюдателя имеются данные только об энтропии (разнообразии) измеряемой переменной (переменных) (H(M)), он может только косвенно оценить работу регулятора Эшби по тому, насколько велика или низка эта энтропия, так сказать, «на выходе» системы. При этом: H(M) ≥ H(Z) ≥ H(D) – H(R). Чем больше информации (порядка) может извлечь сам наблюдатель из этого информационного потока, тем более сложно организован его «регулятор». В этом, собственно, и заключена сущность работы исследователя – поиск порядка на фоне «хаоса» случайных событий и явлений, или, как говорил Ю. Г. Пузаченко, «борьба с энтропией».
Результаты
Рассмотрим конкретные примеры, в которых в качестве объектов исследования выступает совокупность измерений черепа, пястных и плюсневых костей млекопитающих. Основным техническим приемом, позволяющим решить поставленную задачу, является построение многомерной модели (морфопространства) изменчивости первичных измерений методом неметрического многомерного шкалирования (Пузаченко, 2016). Рассмотрены две модели: (1) модель разнообразия размеров черепа и (2) модель разнообразия формы черепа. В первом случае в качестве метрики используем эвклидову дистанцию, во втором – ранговую корреляцию Кендалла (τb).
Распределения параметров разнообразия на рис. 2 построены на основе 126 их значений для моделей морфопространств изменчивости размеров и 126 значений для моделей морфопространств изменчивости формы черепа.
Каждая координата модельного морфопространства (d) может быть интерпретирована как «существенная переменная» морфосистемы «череп». Координаты морфопространства могут интерпретироваться и как «параметры порядка» или «степени свободы» системы в контексте синергетики (Хакен, 1991).
С позиции теории информации число координат модели (размерность) соответствует числу независимых информационных каналов между системой и наблюдателем. Суммарная энтропия (H = ∑Hi) координат модели отражает разнообразие реализованных микросостояний системы «череп» (особей) и поэтому косвенно характеризует работу гипотетического регулятора Эшби на уровне выборки.
Удельная энтропия (Hd = H/d) (см. рис. 2) тоже содержательно связана с пропускной способностью морфорегулятора. После подстановки эмпирических значений в формулу для ЄR получаем, что величина медианы ЄR, «эффективности» регулирования разнообразия размеров черепа, составляет 42.7 %, а его формы – 39 % (см. рис. 2). Чем выше ЄR, тем эффективнее работа регулятора, тем выше его внутреннее разнообразие и пропускная способность как информационного канала и тем ниже энтропия – информация на «выходе» системы.
R – относительно слабо варьирующая переменная (рис. 2); подавляющее число эмпирических значений R существенно меньше критического значения (≈ 0.31, рис. 2 и 3).
Эмпирическая медиана пропускной способности для случая разнообразия размеров черепа составляет 1.17, а для разнообразия его формы – 1.27 (рис. 3).
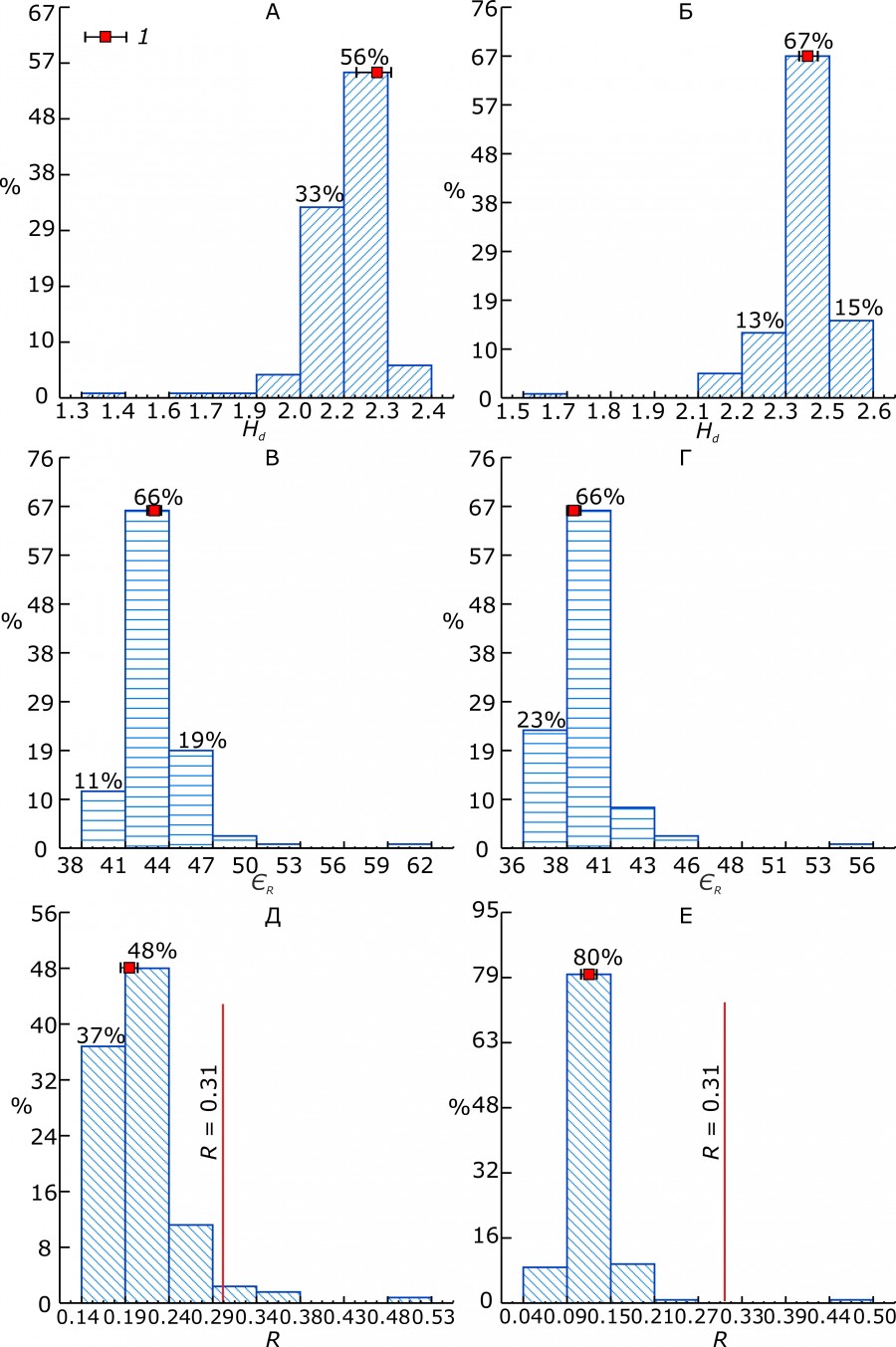
Рис. 2. Распределения величин параметров разнообразия размеров и формы черепа у 35 видов млекопитающих (число моделей морфопространств во всех случаях равно 126): A, Б – Hd, удельная энтропия (H/d) морфосистем разнообразия размеров и формы черепа соответственно; В, Г – ЄR, эффективность регулирования морфосистем системы размеров и пропорций черепа соответственно; Д, Е – R, мера избыточности Шеннона или организации разнообразия морфосистемы размеров и формы черепа соответственно. Все значения параметров приведены (откалиброваны) к стандартному объему выборки (число «элементов» в моделях морфопространств), N = 50 (экземпляров) (Пузаченко, 2016). 1 – медиана и бутстрэп-оценка ее 95 % доверительного интервала: Hd, разнообразие размеров – 2.19, 2.16–2.21, разнообразие формы – 2.39, 2.38–2.40; ЄR, разнообразие размеров – 42.7, 42.3–43.1, разнообразие формы – 39.0, 38.8–39.1; R, разнообразие размеров – 0.193, 0.188–0.199, разнообразие формы – 0.119, 0.115–0.124
Fig. 2. Distributions of the size and shape diversity parameters of the skull in 35 species of mammals (the number of morphospace models is 126 in both cases). A, Б – Hd, specific entropy (H/d) of morphosystems diversity for sizes and shapes of the skull, respectively; В, Г – ЄR, the efficiency of regulation of morphosystem of the skull size and shape system, respectively; Д, E – R, Shannon' redundancy or measure of the organization of morphosystems diversity for the skull sizes and shapes, respectively. All parameter values were calibrated to the standard sample size (the number of "elements" in a morphospace model), N = 50 (specimens) (Puzachenko, 2016). 1 – median value and bootstrap evaluation of its 95 % confidence interval: Hd, size diversity – 2.19, 2.16–2.21, shape diversity – 2.39, 2.38–2.40; ЄR, size diversity – 42.7, 42.3–43.1, shape diversity – 39.0, 38.8–39.1; R, size diversity – 0.193, 0.188–0.199, shape diversity –0.119, 0.115–0.124
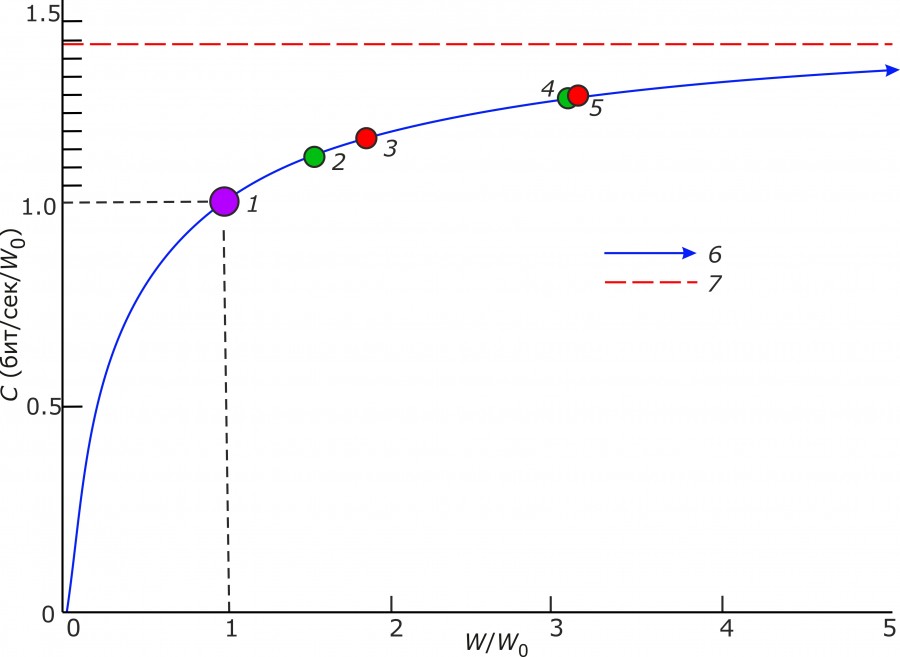
Рис. 3. Зависимость пропускной способности (С) от отношения полосы частот W к полосе частот шума в канале связи (w0) в соответствии с законом Шеннона – Хартли: 1 – пропускная способность при мощности шума, равной мощности сигнала; 2, 4 – медианы С для морфосистем разнообразия размеров (С = 1.12) и пропорций (C = 1.26) посткраниальных элементов (оценка по 71 модели морфопространств) соответственно; 3, 5 – медианы для морфосистем разнообразия размеров (С = 1.17) и пропорций (C = 1.27) черепа (оценка по 126 моделям морфопространств) соответственно; 6 – теоретическая зависимость C от W/W0 (W0 = P/N0); 7 – асимптотическое значение С ≈ 1.443
Fig. 3. Dependence of throughput capacity (С) on the ratio of the frequency band W and frequency of white noise (w0) in accordance with the Shannon – Hartley law: 1 – channel capacity when the noise power is equal to the signal power; 2, 4 – medians of C of diversity morphosystems for sizes (С = 1.12) and shapes (C = 1.26) of postcranial elements (evaluation based on 71 models of morphospace), respectively; 3, 5 – medians of C for size (C = 1.17) and shape (C = 1.27) diversity of the skull (evaluation based on 126 models of morphospace), respectively; 6 – theoretical dependence between C and W/w0; 7 – asymptotic value of C ≈ 1.443
Относительно черепа, состоящего из множества костей, метаподии и таранная кость представляют собой заведомо более простые морфологические структуры. Это отражается в более высоком, чем у черепа, значении R в случае разнообразия размеров (медиана – 0.227) (рис. 3). Однако этот детерминизм отчасти компенсируется относительно низким значением R разнообразия формы этих костей (0.122), близким к значению R для черепа (0.119).
То, что самоорганизация не обязательно связана с ростом внутреннего порядка, а напротив, предполагает непостоянство величины организованности, продемонстрируем на примере постнатального онтогенеза черепа бобра и обыкновенного слепыша (рис. 4). Для обоих видов в процессе роста черепа до половозрелой стадии отмечаются сильные флуктуации меры организованности как размеров, так и формы черепа. У взрослых животных величина R не остается постоянной, но ее изменения происходят в трех случаях из четырех с меньшей амплитудой.
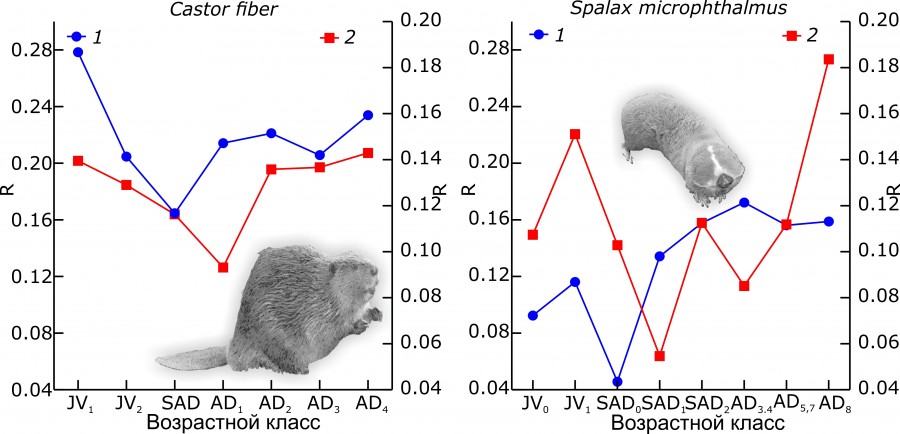
Рис. 4. Изменение меры организации (R) разнообразия размеров (1) и формы (2) черепа евразийского бобра и обыкновенного слепыша в постнатальном онтогенезе. Все значения параметров приведены (откалиброваны) к стандартному объему выборки (число «элементов» в моделях морфопространств), N = 50 (экземпляров) (Пузаченко, 2016)
Fig. 4. Changes in measure of organization (R) of the size (1) and shape (2) diversity of the skull in Eurasian beaver and greater mole-rat in postnatal ontogeny. All values of R were calibrated to the standard sample size (the number of "elements" in a morphospace model), N = 50 (specimens) (Puzachenko, 2016)
Обсуждение
Обе полученные нами величины C для разнообразия размеров и формы черепа лежат выше критического значения 1. Следовательно, регулятор не обеспечивает жесткий контроль размеров или пропорций черепа, но поддерживает относительно высокое разнообразие морфологической системы в целом (разнообразие на уровне выборки). Реализованная пропускная способность регулятора (H(R)) обеспечивает, вероятно, оптимальное соотношение между разнообразием сигналов, поступающих из «среды» (H(D)), и величиной результирующего разнообразия системы (H(Z)), при котором морфологическая система остается в стационарном режиме.
Около 80 % эмпирических значений R лежат в интервалах 0.1–0.25 (разнообразие размеров) и 0.09–0.15 (разнообразие формы). Для систем с R > 0.3 типично детерминированное поведение и высокая эффективность работы регулятора, которая ограничивается только его пропускной способностью. Для систем с R < 0.1 предполагается доминирование стохастического (вероятностного) поведения и низкая эффективность саморегулирования. Соответственно, морфологическая система черепа млекопитающих относится к третьей, промежуточной категории, а именно к категории вероятностно-детерминированных систем (Бир, 1963). Другими словами, исследованные системы «балансируют» между гранями хаоса и порядка.
Рассмотренный нами пример, вероятно, иллюстрирует общую, фундаментальную закономерность – ограничение возможности эффективности саморегуляции по мере роста сложности организации систем. Это ограничение, в свою очередь, приводит к необходимости возникновения внутренней иерархии в системе, позволяющей частично преодолеть его (Aulin, 1979).
В целом степень внутренней организованности (упорядоченности, детерминизма) обратно пропорциональна сложности системы. Для живой формы материи (живого вещества) это утверждение означает, что его разнообразие содержит две компоненты – случайную (стохастическую) и упорядоченную (детерминированную, «запомненную»). Именно сочетание обоих компонент создает предпосылки для адаптации и эволюции. Эволюция в направлении усиления детерминированной компоненты (самоупорядочивания) есть не что иное, как специализация. Однако сильно специализированные системы с очень эффективным регулятором, с высокой пропускной способностью теряют способность к адекватной реакции на глобальные долговременные изменения в среде или на локальное усиление мощности сигнала из среды. В результате они обречены на относительно быстрое вымирание или на существование в рамках очень узкой экологической ниши.
Результаты исследований постнатального онтогенеза черепа не поддерживают гипотезу о непрерывном возрастающем уровне внутреннего «порядка» в процессе самоорганизации (в данном случае онтогенеза) сложных систем (Ashby, 1962), но поддерживают представление о разной роли стохастической и детерминированной компонент разнообразия в этом процессе, характеризующемся сменой более и менее упорядоченных состояний.
В заключение рассмотрим модель, развиваемую в серии работ Ю. Г. Пузаченко (Пузаченко Ю., 1982, 1992, 2006, 2007, 2009, 2016) на основе теоретических построений статистической термодинамики (термостатики), в том числе нелинейной, и теории информации. В рамках информационной интерпретации принимается, что пропускная способность канала связи есть функция мощности действия «окружающей среды», влияющей на систему. Ошибки биологической системы в восприятии средового сигнала могут выступать фактором, ограничивающим выживание (приспособленность). Причиной ошибок является «шум» (с очень широкой содержательной нагрузкой этого понятия). Как следует из теории, ошибка есть функция ширины полосы частот. Далее, постулируется стремление системы максимизировать время пребывания в стационарном состоянии. Из закона о пропускной способности следует, что одним из способов повышения устойчивости является уменьшение полосы частот (аналог – размерность системы), т. е. снижение шума. Следствием этого является снижение скорости передачи информации, что, в свою очередь, уменьшает внутреннее разнообразие системы и может приводить к потере устойчивости. Следовательно, при заданной мощности средового сигнала должна существовать некоторая оптимальная полоса частот, для которой внутреннее разнообразие (сложность) системы достаточно для обеспечения ее устойчивости.
Максимизируя устойчивость в заданных условиях среды, система достигает определенного уровня специализации, но только такого, который достаточен для поддержания необходимой для выживания минимальной пропускной способности регулятора: Csust = log2P/W, где W = kwi – полоса частот всей системы (полосы частот wi у разных каналов не перекрываются). Таким образом, при большом k, чем больше мощность среды, тем больше может быть число разнородных классов систем (например, видов в сообществе, подвидов в ареале вида и т. д.).
В рассматриваемой модели предельное число специализированных каналов i (число степеней свободы, размерность системы) есть функция среды, а их возникновение и общая информация в системе рассматриваются как результат самоорганизации в паре «среда – система».
Для особей внутри популяции одного вида внутривидовые взаимодействия выступают наряду с другими в качестве сигналов «среды». В этом случае мощность сигнала будет пропорциональна плотности популяции. Модель с такими начальными условиями может иметь информационную интерпретацию, аналогичную приведенной выше. Одним из следствий модели будет, например, разделение пространства между особями или времени активности разных половозрастных групп и т. п. В случае положительных взаимодействий (например, образования группировок или стай у животных и, возможно, тесных одновидовых сообществ у растений) возникают системы более высокого уровня сложности, имеющие возможность существенно увеличить полосу частот приема сигналов из среды без существенного относительного прироста шума и возможности к дальнейшей самоорганизации. Результатом может стать рост устойчивости (выживания) образующих ее особей и самой системы в целом. Аналогичная логика может быть применена и в моделях межвидовых взаимодействий на уровне экосистемы.
Выражение для пропускной способности канала связи используется (Пузаченко Ю., 2009) для оценки роста таксономического разнообразия семейств в масштабе эволюционного времени. Рост разнообразия описывается гипергеометрической зависимостью. Рост затрат энергии на основной обмен описывается экспоненциальной зависимостью (Зотин, Зотин, 1999). Таким образом, рост структурного разнообразия живого вещества опережает рост внутренних энергетических затрат (диссипированной энергии) на его поддержание. На основании допущения оптимизации соотношения роста информации и энергетических затрат (бит/дж) Ю. Г. Пузаченко (1976) сформулировал гипотезу от том, что в процессе макроэволюции оно должно снижаться. Модель предсказывает наличие длительного латентного состояния с последующим относительно быстрым синтезом таксономического разнообразия. Ю. Г. Пузаченко предполагал, что в это время происходит «стохастический поиск удачных устойчивых комбинаций элементов, на основе запоминания которых возникает основание для убыстрения синтеза новых форм».
Следуя принятой выше аксиоматике (Пузаченко, 2016), результаты нашего исследования, в случае их справедливости, должны находиться в соответствии с наблюдаемой эволюцией разнообразия стандартной материи в целом. На рис. 5 очень схематично изображен эволюционный рост разнообразия материи от условного момента «большого взрыва» до «современности», как она реализуется на нашей планете. Наиболее адекватная функция зависимости логарифма числа разнокачественных материальных систем (от элементарных частиц до видов) от логарифма времени имеет, скорее всего, S-образную форму. При этом действительно можно выделить «латентный период» между образованием элементарных частиц и возможностью синтеза атомов химических элементов, а затем простых веществ. Максимальное разнообразие стандартной материи объективно связано с живым веществом. Вероятно, на этом уровне и достигается «технический» предел сложности ее организации.
Обращает на себя внимание обратная зависимость между сложностью материальных систем, энергий их взаимодействия и температурой. Как известно, биологические системы способны взаимодействовать с относительно низкими энергетическими затратами по сравнению с неживыми системами, но при этом могут существовать только в относительно узком диапазоне температур (и других физических переменных).
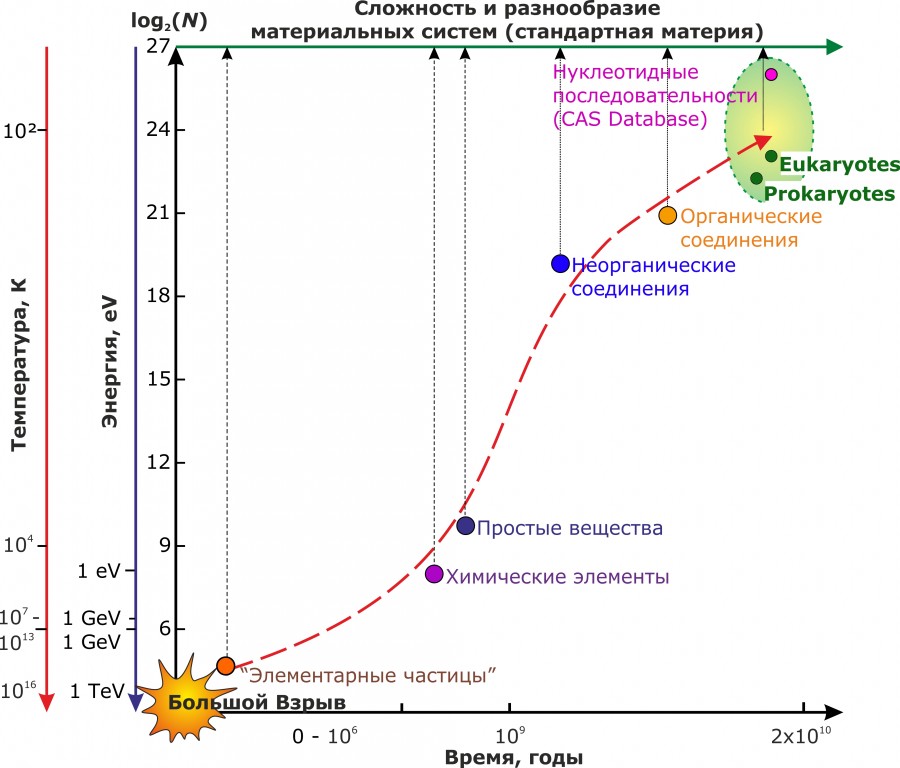
Рис. 5. Обобщенная схема увеличения разнообразия стандартной материи
Fig. 5. Generalized scheme for increasing the diversity of standard matter
Заключение
Биологические системы относятся к особому классу физических систем, которые характеризуются способностью одновременно и к самоорганизации, и к эволюции. Есть ли пределы структурной упорядоченности подобных сложных систем? На этот вопрос мы склонны дать положительный ответ. Биологические и социальные системы «максимизируют» свою устойчивость за счет специализации по отношению к вещественно-информационным ресурсам среды, что сопровождается/обеспечивается усилением внутреннего порядка и ростом эффективности механизмов регуляции. Упорядоченность, а после определенного предела переупорядоченность снижают возможности системы к восприятию изменений во внешней среде и одновременно способность к эволюционным преобразованиям. В конечном итоге такие высоко адаптированные к определенным условиям системы теряют устойчивость даже к небольшим возмущениям среды, за пределами значений параметров их узкой ниши. «Возникновение когерентного поведения специализированных… частных (информационных. – А. П.) каналов приводит к большой чувствительности, к малым возмущением всей системы и к высокой вероятности ее перехода в хаотическое термодинамически равновесное состояние и к гибели отдельных гиперспециализированных подсистем» (Пузаченко Ю., 2009).
Уровень внутренней упорядоченности исследованных нами в качестве примера морфологических систем позволяет отнести их к категории вероятностно-детерминированных (квазидетерминированных). Костные структуры, особенно сложные и полифункциональные, такие как череп млекопитающих, обычно демонстрируют высокую коррелированность изменчивости отдельных «элементов». Однако даже в этих случаях эффективность работы их обобщенного регулятора Эшби оказалась не столь высока, как этого можно было бы ожидать. В целом они не существуют в режиме детерминированного управления. Для менее интегрированных сложных систем можно ожидать еще более низкой относительной эффективности работы регулирующих механизмов.
Промежуточный вариант решения «проблемы» устойчивости состоит в усложнении внутренней иерархии системы, с разделением целей управления на разных уровнях при усилении роли «горизонтальных» информационных и вещественных потоков. Это повышает внутреннее разнообразие системы, но может способствовать ее переходу в хаотическое состояние при возникновении дефицита существенных ресурсов. При этом внутри каждого уровня иерархии и, следовательно, на уровне системы в целом сохраняются все ограничения, вытекающие из закона Шеннона – Хартли. Кроме этого возникают аналогичные проблемы при передачи информации между иерархическими уровнями.
Формальное ограничение на рост внутреннего порядка сложной системы вытекает из закона о предельной пропускной способности информационного канала связи, если сводить модель системы к модели ее регулятора. Закон Шеннона – Хартли определяет предел возможности роста пропускной способности (сложности) регулятора, а в качестве следствия этого ограничения – возможности самоупорядочивания.
Подчеркнем, что процесс самоорганизации не сводятся только к самоупорядочиванию. Помимо этой компоненты он включает в себя противоположно направленную компоненту разупорядочивания. Обе компоненты могут находиться в разных отношениях в пространстве и во времени.
Отметим в заключение, что в социальных системах неоднократно предпринимались и предпринимаются попытки перехода к типу «вертикального» управления. Все они в конечном итоге заканчивались в прошлом разрушением таких «переупорядоченных» социумов. При этом на сопоставимых исторических интервалах времени эти социальные системы могли быть локально успешными за счет потребления (по большей части малоэффективного) огромного количества ресурсов из внешней по отношению к ним среды.
Библиография
Бир С. Кибернетика и управление производством . М.: Физматгиз, 1963. 275 с.
Бриллюэн Л. Наука и теория информации . М.: Гос. изд-во физико-математической лит-ры, 1960. 392 с.
Винер Н. Кибернетика, или управление и связь в животном и машине . 2-е изд. М.: Наука, 1983. 344 с.
Зотин А. И., Зотин А. А. Направление, скорость и механизмы прогрессивной эволюции: Термодинамические основы . М.: Наука, 1999. 317 с.
Майнцер К. Сложносистемное мышление: Материя, разум, человечество. Новый синтез . М.: Книжный дом «ЛИБРОКОМ», 2009. 464 с.
Пузаченко А. Ю. Внутрипопуляционная изменчивость черепа обыкновенного слепыша Spalax microphthalmus (Spalacidae, Rodentia). 1. Методика анализа данных, невозрастная изменчивость самцов // Зоологический журнал. 2001. Т. 80 (3). С. 1–15.
Пузаченко А. Ю. Инварианты и динамика морфологического разнообразия (на примере черепа млекопитающих) : Дис. … д-ра биол. наук. М., 2013. 417 с.
Пузаченко А. Ю. Информационные переменные морфометрического разнообразия млекопитающих // Териофауна Россия и сопредельных территории: Материалы Междунар. совещ. (IX Съезд Териологического общества при РАН). М.: Товарищество научных изданий КМК, 2011. С. 384.
Пузаченко А. Ю. Количественные закономерности морфологического разнообразия черепа млекопитающих // Сборник трудов Зоологического музея МГУ. Т. 54 / Под ред. И. Я. Павлинова, М. В. Калякина, А. В. Сысоева. М.: Товарищество научных изданий КМК, 2016. С. 229–268.
Пузаченко А. Ю. Применение многомерного шкалирования в анализе структуры морфологической изменчивости // Систематика и филогения грызунов и зайцеобразных / Под ред. А. К. Агаджаняна, В. Н. Орлова. М.: РАСХН, 2000. С. 137–140.
Пузаченко Ю. Г. Проблемы исследования биологического разнообразия горных территорий // Млекопитающие горных территорий: Материалы Междунар. конф. М.: Товарищество научных изданий КМК, 2007. C. 256–266.
Пузаченко Ю. Г. Биологическое разнообразие в биосфере: системологический и семантический анализ // Биосфера. 2009. Т. 1 (1). С. 025–038.
Пузаченко Ю. Г. Биологическое разнообразие, устойчивость и функционирование // Проблемы устойчивости биологических систем. М.: ИЭМЭЖ АН СССР, 1982. С. 5–32.
Пузаченко Ю. Г. Глобальное биологическое разнообразие и его пространственно-временная изменчивость // Современные глобальные изменения природной среды. Т. 2. М.: Научный мир, 2006. С. 306–377.
Пузаченко Ю. Г. Общие метологические вопросы информации // Экоинформатика. Теория. Практика. Методы и системы / Под ред. акад. В. Е. Соколова. СПб.: Гидрометеоиздат, 1992. С. 7–84.
Пузаченко Ю. Г. Принципы анализа информации // Статистические методы исследования геосистем. Владивосток, 1976. С. 38–46.
Пузаченко Ю. Г. Ранговые распределения в экологии и неэкстенсивная статистическая механика // Сборник трудов Зоологического музея МГУ. Т. 54 / Под ред. И. Я. Павлинова, М. В. Калякина, А. В. Сысоева. М.: Товарищество научных изданий КМК, 2016. С. 42–71.
Хакен Г. Информация и самоорганизация: Макроскопический подход к сложным явлениям . М.: Мир, 1991. 240 с.
Abramov A. V., Puzachenko A. Y. Species Co-Existence and Morphological Divergence in West Siberian Mustelids (Carnivora, Mustelidae) // Mammal Study. 2012. Vol. 37 (3). P. 255–259.
Ashby W. R. Principles of the self-organizing system // Principles of Self-organization: Transactions of the University of Illinois Symposium / Eds. H. Von Foerster, G. W. Zopf. London: Pergamon Press, 1962. P. 255–278.
Ashby W. R. An introduction to cybernetics. London: Chapman & Hall, 1956. 295 p.
Ashby W. R. Requisite variety and its implications for the control of complex systems // Cybernetica. 1958. Vol. 1 (2). P. 83–99.
Ashby W. R. Principles of the self-organizing dynamic system // Journal of General Psychology. 1947. Vol. 37. P. 125–128.
Atlan H. Sources of Information in Biological Systems // IFAC Proceedings Volumes. 1977. Vol. 10 (12). P. 177–184.
Collier J. Information in Biological Systems // Handbook of Philosophy of Science. Vol. 8: Philosophy of Information. Amsterdam: Elsevier, 2008. P. 763–787.
Conant R. C., Ashby R. W. Every good regulator of a system must be a model of that system // International Journal of Systems Science. 1970. Vol. 1 (2). P. 89–97.
Foerster H. von. On Self-Organizing Systems and Their Environments // Self-Organizing System. 1960. Vol. 50. P. 31–50.
Hartley R. V. L. Transmission of Information // Bell System Technical Journal. 1928. Vol. 7 (3). P. 535–563.
Hawking S. The Theory of Everything: The Origin and Fate of the Universe. California, Beverly Hills: New Millenium Press, 2002. 176 p.
Mayr E. What evolution is. NY: Basic Books, 2001. 318 p.
McCowan B., Hanser S. F., Doyle L. R. Using information theory to assess the diversity, complexity, and development of communicative repertoires // Journal of Comparative Psychology. 2002. Vol. 116 (2). P. 166–172.
Nyquist H. Certain Factors Affecting Telegraph Speed // Bell System Technical Journal. 1924. Vol. 3 (2). P. 324–346.
Nyquist H. Certain Topics in Telegraph Transmission Theory // Transactions of the American Institute of Electrical Engineers. 1928. Vol. 47 (2). P. 617–644.
Puzachenko A. Y., Korablev N. P. Morphological diversity in the postnatal skull development in representatives of two families of rodents (Spalacidae, Castoridae, Rodentia) // Russian Journal of Developmental Biology. 2014. Vol. 45 (3). P. 149–162.
Puzachenko A. Y., Markova A. K. Using multidimensional analysis and information functions for macro description of European natural complexes in the second part of the Late Pleistocene and the Holocene // Doklady Earth Sciences. 2011. Vol. 437 (1). P. 380–382.
Puzachenko J. G. Information and information flows in the biosphere // Encyclopedia of Ecology / Eds. S. E. Jørgensen, B. D. Fath. Oxford: Elsevier, 2008. P. 108–110.
Schneider T. D. Evolution of biological information // Nucleic Acids Research. 2000. Vol. 28 (14). P. 2794–2799.
Schrödinger E. What is Life? The Physical Aspect of the Living Cell. N. Y.: Cambridge University Press, 2012. P. 1–90.
Shannon C. E. A Mathematical Theory of Communication // Bell System Technical Journal. 1948. Vol. 27. P. 379–423, 623–656.
Shannon C. E. Communication in the Presence of Noise // Proceedings of the IRE. 1949. Vol. 37 (1). P. 10–21.
Shannon C. E., Weaver W. The mathematical theory of communication. Urbana, IL: University of Illinois Press, 1949. 35 p.
Tkačik G., Bialek W. Information Processing in Living Systems // Annual Review of Condensed Matter Physics. 2016. Vol. 7 (1). P. 89–117.
Благодарности
Статья подготовлена по теме Государственного задания 0148-2019-0007 (АААА-А19-119021990093-8) «Оценка физико-географических, гидрологических и биотических изменений окружающей среды и их последствий для создания основ устойчивого природопользования».






 © 2011 - 2026
© 2011 - 2026