Введение
В своей лекции по современному состоянию количественных методов в фитоценологии (Розенберг, 2007), которую вполне можно было бы назвать «Мы все вышли из монографии Грейг-Смита», я вкратце описал некоторые методы фрактального анализа, используемые в экологии (Morse et al., 1985; Dicke, Burrough, 1988; Sugihara., May, 1990; Green, 1991; Scheuring, 1991; Zeide, 1991; Scheuring, Riedi, 1994; Пузаченко, Пузаченко, 1996; Seuront et al., 1996; Turchin, 1996; Азовский, Чертопруд, 1997, 1998; Пузаченко, 1997; Pachepsky, Ritchie, 1998; Pachepsky, Timlin, 1998; Harte et al., 1999; With et al., 1999; Чертопруд, Азовский, 2000; Azovsky, 2000; Azovsky et al., 2000; Pachepsky et al., 2000a, b; Li, 2000; Иудин, Гелашвили, 2002; Brown et al., 2002; Iudin, Gelashvili, 2003; Иудин и др., 2003; Розенберг и др., 2003а, б, 2007; Green et al., 2003; Гелашвили и др., 2004, 2006а, б, 2007а, б, в; Bossuyt, Hermy, 2004; Иудин, 2006; Laurie, Perrier, 2006; Zhang et al., 2006; Gelashvili et al., 2007). Прошло десять лет и сегодня можно подводить некоторые итоги, констатировать, что модели фрактальной геометрии все шире находят свое приложение в экологических исследованиях (см.: Гелашвили и др., 2008а,б,в, 2009а, б, в, 2010а, б, 2011, 2012, 2013а, б; Иудин и др., 2010; Iudin et al., 2010; Seuront, 2010; Розенберг, 2013; Якимов и др., 2014а, б, в, 2016а, б, 2017; Yakimov et al., 2014 и мн. др.), и рекомендовать этот подход к более широкому применению как в геоботанических, так и экологических исследованиях.
Аналитический обзор
Несколько слов о Бенуа Мандельброте
Сначала – небольшой панегирик.
| «Вспоминая славные имена прошлого, мы не должны забывать о нашем великом современнике, несравненном Бенуа Мандельброте… Как выяснилось, все эти годы мы жили с фрактальными артериями неподалеку от фрактальных речных систем, собирающих влагу со склонов фрактальных гор под фрактальными облаками и катящих свои воды к фрактальным берегам морей и океанов. Но как и мольерову мещанину во дворянстве, нам не доставало надлежащей прозы – существительного фрактал и прилагательного фрактальный (выделено автором. – Г.Р. и др.), который мы обрели благодаря Бенуа Мандельброту» (Шредер, 2001, с. 18–19).
В четверг, 14 октября 2010 г., в городе Кембридж (штат Массачусетс, США) после продолжительной и тяжелой болезни скончался выдающийся математик, создатель нового направления в геометрии – фрактальной геометрии, профессор Бенуа Мандельброт. Разработанная им теория фракталов оказала существенное влияние на разные области человеческой деятельности и знания – компьютерную графику, финансы, экологию и др. Некрологи о нем поместили такие влиятельные газеты и журналы, как «New York Times» и «The Atlantic» (США), «Telegraph» и «Guardian» (Великобритания), «Le Monde» (Франция) и др. |
 |
«Если Вы знаете начало и конец, то у меня была самая обычная карьера», – говорил Мандельброт в Йельском университете на церемонии присуждения ему почетного звания Sterling[1] Professor of Mathematical Sciences. – «Но это не была прямая линия между началом и концом. Это была очень изогнутая, фрактальная кривая» (http://mathnotations.blogspot.com/search/ label/mandelbrot).
Бенуа Мандельброт (фр. Benoît B. Mandelbrot) родился 20 ноября 1924 г. в Варшаве в семье литовских евреев. Его отец был галантерейщиком, а мать – врачом. В 1936 г. вся семья, спасаясь от нацистов, эмигрировала на юг Франции (городок Тюль [Tulle]), а потом перебралась и поселилась в Париже. Здесь Бенуа попал под влияние своих дядей[2], которые и заинтересовали его математикой. При этом выяснилось, что у Бенуа великолепное пространственное воображение – даже алгебраические задачи он решал геометрическим способом. Он поступает в Политехническую школу в Париже, а сразу после войны становится студентом Сорбонны, где обучается под руководством Гастона Жулиа [Gaston M. Julia] и Пауля Леви [Paul Lévy]. После окончания Сорбонны Мандельброт переезжает в США, где заканчивает Калифорнийский технологический институт. По возвращении во Францию в 1952 г. он защищает ученую степень PhD по математике в Парижском университете, в 1955 г. женится на Альетт Каган [Aliette Kagan] и переезжает в Женеву, «наездами» в Принстоне повышает свою квалификацию у Дж. фон Неймана [John von Neumann][3], а в 1958 г. окончательно поселяется в США, где приступает к работе в научно-исследовательском центре IBM (T. J. Watson Research Center) в Йорктауне [Yorktown Heights].
В IBM Мандельброт проработал 35 лет и 12 дней (до 1987 г.). Первоначально он занимался вопросами «чистой» математики. Потом решает задачу исследования ошибок, возникающих при передаче компьютерной информации по телефонным каналам связи компании. Анализируя природу этих, казалось бы, совершенно случайных ошибок, Мандельброт находит периоды их появления и определяет самоподобную структуру этих периодов: ошибки не появляются хаотично, а «собираются» в серии-кластеры; каждый кластер состоит из своих кластеров. Это открытие позволило не только сохранить компании огромные денежные средства на преодоление помех, но и стало первым толчком для нового, геометрического осмысления мира. Работая в IBM, Мандельброт все дальше и дальше уходит в сторону от чисто прикладных проблем компании. Он работает в области лингвистики, теории игр, экономики, аэронавтики, географии, физиологии, астрономии, физики… и не раз оставляет еще не законченные исследования ради нового, «не освоенного» им раздела науки. Так, например, еще в 1951 г. Мандельброта «слегка заинтересовала закономерность, описывающая частотность употребления слов в речи, называемая законом Ципфа, причем узнал я о ней из книжного обозрения… Упомянутое обозрения я выудил из корзины для ненужных бумаг одного "чистого" математика, имея в виду разжиться легким чтением на время поездки в парижском метро. Закон Ципфа оказалось несложно объяснить, а в качестве побочного эффекта моя работа поспособствовала рождению новой дисциплины – математической лингвистики» (Мандельброт, 2002, с. 584–585). В экономике Мандельброт обнаружил, что внешне произвольные (случайные на вид) колебания цены на хлопок за большой временной интервал (более ста лет) следуют скрытому математическому порядку во времени, который не описывается стандартными кривыми; он проследил симметрию в длительных и кратковременных колебаниях цены. Это открытие оказалось неожиданностью для экономистов. Как говорится, «процесс пошел» и «я начал обращать внимание на аналогичные эмпирические закономерности в различных областях человеческой деятельности…» (Мандельброт, 2002, с. 585).
В середине 60-х годов Мандельброт задал себе вопрос: какой длины побережье Великобритании (Mandelbrot, 1967)? Оказалось, что все зависит от инструмента, с помощью которого эта длина будет измеряться. Опыт показывает, что длина береговой линии L зависит от масштаба l, которым проводятся измерения, и увеличивается с уменьшением последнего по степенному закону
L = Λ l-α, Λ = const.
Так, например, для побережья Великобритании α ≈ 0,3. Происхождение такой зависимости понятно: чем меньше масштаб мы используем, тем меньшие детали побережья будут учтены и дадут вклад в измеряемую длину (рис. 1). Наоборот, увеличивая масштаб, мы «спрямляем» побережье, уменьшаем тем самым его длину L. Таким образом, «понятие "длины" обычно бессмысленно для географических кривых» (Mandelbrot, 1967, p. 636).
Рис. 1. Береговая линия побережья Великобритании (http://en.wikipedia.org/wiki/Lewis_Richardson)
Fig.1. Coastal line of the Great Britain
В 1975 г.[4] в изданной во Франции книге «Les objets fractals: forme, hasard et dimension» Мандельброт вводит в научный оборот понятие «фрактал»[5]. «Термин фрактал я образовал от латинского причастия fractus. Соответствующий глагол frangere переводится как ломать, разламывать, т. е. создавать фрагменты неправильной формы. Таким образом, разумно – и как кстати! – будет предположить, что, помимо значения "фрагментированный" (как, например, в словах фракция или рефракция), слово fractus должно иметь и значение "неправильный по форме"» (Мандельброт, 2002, с. 18). Иными словами, «вырезав» небольшую часть из структуры, имеющей свойства фрактальности, можно рассмотреть ее в некотором увеличении и обнаружить, что она подобна всей структуре в целом; выделив еще более мелкую часть из уже вырезанной части и увеличив ее, опять обнаружим, что и она подобна первоначальной структуре. Для идеальной фрактальной структуры такую операцию можно проделывать до бесконечности, и даже самые микроскопические частички будут подобны структуре в целом. Самоподобие предполагает, что копирование и масштабирование некоторого «эталонного» образа позволяет природе легко создавать сложную многомасштабную структуру. Реальные объекты имеют довольно четко ограниченный интервал масштабов, в которых они проявляют свою фрактальную природу.
«Фракталы вокруг нас повсюду, и в очертаниях гор, и в извилистой линии морского берега. Некоторые из фракталов непрерывно меняются, подобно движущимся облакам или мерцающему пламени, в то время как другие, подобно деревьям или нашим сосудистым системам, сохраняют структуру, приобретенную в процессе эволюции» (Пайген, Рихтер, 1993, с. 7). А вот еще одна цитата из работы В. Н. Беклемишева (1964, с. 37): «…живой организм (и экосистема. – Г.Р. и др.) не обладает постоянством материала – форма его подобна форме пламени, образованного потоком быстро несущихся раскаленных частиц; частицы сменяются, форма остается». Иными словами, подобно мольеровскому Журдену, экологи давно «говорят прозой» (о фракталах), не догадываясь об этом… И вновь Мандельброт (2002, с. 13): «Облака не являются сферами, горы – конусами, береговые линии нельзя изобразить с помощью окружностей, кору деревьев не назовешь гладкой, а путь молнии – прямолинейным. В более общем виде я заявляю, что многие формы Природы настолько неправильны и фрагментированы, что в сравнении с евклидовыми фигурами… Природа демонстрирует не просто более высокую степень, но совершенно иной уровень сложности». Пример фрактального множества, ставшего классическим, приведен на рис. 2.
Рис. 2. Фрактальное множество Мандельброта, иногда называемое его автографом
Fig.2. Fractal set of Mandelbrot called sometimes his autograph
В арсенале современной математики Мандельброт нашел удобную количественную меру «неидеальности объектов» – извилистости контура, морщинистости поверхности и пористости объема (ее предложили два математика – Ф. Хаусдорф [Felix Hausdorff, 1868–1942] и А. С. Безикович [1891–1970]), которая носит сегодня имена своих создателей (размерность Хаусдорфа – Безиковича [она же – хаусдорфова размерность]). Как и любая количественная характеристика, эта размерность прошла проверку на работоспособность. В предельных случаях (применительно к идеальным объектам классической евклидовой геометрии) она давала те же численные значения, что и известная задолго до нее, так называемая топологическая размерность (иначе говоря, была равна нулю для точки, единице – для гладкой плавной линии, двум – для «ровной» фигуры и поверхности, трем – для тела и пространства). Однако новая размерность обладала более тонкой чувствительностью ко всякого рода несовершенствам реальных объектов, позволяя различать то, что прежде было безлико и неразличимо – степень «извилистости». Но самое непривычное[6] в размерности Хаусдорфа – Безиковича состоит в том, что она может принимать не только целые, но и дробные значения (именно чтобы подчеркнуть эту способность такого рода размерностей, Мандельброт и предложил называть их фрактальными размерностями).
Если «перевести» вышеизложенные рассуждения на «экологический язык», мы имеем дело с примером противостояния дискретности и континуума при описании сложных систем (в том числе и экологических; см., например: Миркин, Наумова, 1998; Шитиков и др., 2005, кн. 1, с. 77): топологическая размерность – дискретна (увеличивает свое значение скачком), фрактальная – непрерывна. И в этом контексте у фрактальной размерности Мандельброта открываются дополнительные методологические перспективы.
Интересно отметить, что само определение понятия «фрактал» («фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому») предоставляет пищу для системологических рассуждений. Действительно, в своей монографии Мандельброт (2002, с. 31) дает математически более корректное определение: «...фракталом называется множество, размерность Хаусдорфа – Безиковича которого строго больше его топологической размерности». Это определение достаточно строго в математическом плане; однако именно это и является его недостатком, поскольку оно требует определения еще и понятий размерности (топологической и хаусдорфовой), к тому же оно исключает многие классы фрактальных объектов, встречающиеся в различных областях. Однако все виды математических фракталов являются абстракциями, непосредственное применение которых для описания реальных объектов возможно только с некоторыми оговорками. Математическое фрактальное множество, как это следует из его определения, должно обладать некоторыми «неестественными» свойствами (например, у него должны отсутствовать наибольший и наименьший масштабы самоподобия). С другой стороны, в любой физической структуре должен существовать конечный наименьший масштаб. Кроме того, такая структура всегда ограничена в занимаемом ею пространстве, что приводит к нарушению самоподобия вблизи границы (достаточно малая область, содержащая границу множества, не подобна области того же размера, находящейся вдали от границы). «Сила понятия фрактальной размерности, по Хаусдорфу, в том, что она позволяет различать категории "гладкий" и "хаотичный". Слабость же ее в том, что не удается различить категории "нерегулярный, но самоподобный" и "геометрически хаотичный". Это происходит из-за того, что определение является весьма общим, что и требуется для математики. Но для конкретной области науки общий характер этого определения оказывается чрезмерным: оно становится не только неудобным, но и совершенно неподходящим» (Мандельброт, 1993, с. 139). Иными словами, на примере определения понятия «фрактал» хорошо иллюстрируется один из важных системологических принципов – принцип несовместимости Заде [Lotfi Ali Asker Zadeh, 1921–2017]: чем глубже анализируется реальная сложная система, тем менее определенны наши суждения о ее поведении (Розенберг и др., 1999). Поэтому для решения задачи о фрактальности, например, видовой или родовой структуры сообщества, вполне подходящим является первое (может быть, более вербальное) определение фрактала. Можно сказать, что фрактальный объект статистически единообразен в широком диапазоне масштабов. В идеальном случае (математический фрактал) такое самоподобие приводит к тому, что фрактальный объект оказывается инвариантным относительно масштабных изменений пространства (растяжений и сжатий; см., например: Гелашвили и др., 2007в, 2008б).
Другим важным свойством фракталов является их иерархичность, т. е. способность повторяться в разных масштабах пространства и времени. Существует четкий критерий принадлежности объекта к фракталам – объект нельзя считать фрактальным, если он не обладает свойством самоподобия, но можно – если он не иерархичен.
Кроме самоподобия и иерархичности, диагностическими признаками фрактального объекта являются (Федер, 1991; Шредер, 2001; Морозов, 2004):
- Степенная зависимость числа структурных элементов от масштаба, поскольку математическим выражением самоподобия являются степенные законы вида:
f(x) = cxα.
- Масштабная инвариантность (скейлинг; от англ. scaling – масштабирование) – возможность воспроизводить объект при изменении масштабов.
- Строгое отличие фрактальной размерности (α), которая может быть как целочисленной, так и дробной (например, размерность α = 2.87), от топологической (всегда целочисленной). «Фракталы были чужды уютному евклидовому миру с его регулярными структурами» (Макаренко, 2002, с. 122)[7].
Для реального природного фрактала существует некоторый минимальный масштаб длины lmin, такой, что на расстояниях l » lmin его основное свойство – самоподобие – пропадает. Кроме того, на достаточно больших масштабах длин l > lmax, где lmax – характерный геометрический размер объектов, это свойство самоподобия также нарушается. Поэтому свойства природных фракталов рассматриваются лишь на масштабах l, удовлетворяющих соотношению lmin < l < lmax.
Продолжим краткое жизнеописание Бенуа Мандельброта. Параллельно с работой в IBM, «я стал популярным в разных крупных университетах как visiting professor, но ни один из них не хотел видеть меня на постоянной должности в силу непредсказуемости моих [научных] интересов[8]. Однажды, когда я все еще был относительно молодым, я получил от одного из ведущих американских университетов очень очаровательное предложение, от которого отказались на другой день, как только декан заинтересовался моей профессиональной деятельностью в других [смежных с математикой] областях» (A maverick’s apprenticeship..., 2004). В это же время (1974 г.) Мандельброту присваивается звание Почетного сотрудника IBM (IBM Fellow)[9], которое является самым высоким знаком отличия для технических специалистов компании и признанием их выдающихся технических достижений и лидерства в таких областях, как проектирование, программирование, услуги, научная деятельность и технологии. Почетным сотрудникам предоставляются более широкие возможности, чтобы поддерживать их деятельность по разработке инноваций (Мандельброт возглавляет небольшую группу).
Только с 1987 г., после ухода из IBM, Мандельброт начал систематически преподавать на математическом факультете Йельского университета, а штатным профессором стал лишь в 1999 г. Как он сам отметил (A maverick’s apprenticeship..., 2004): «Йельский университет, возможно, следует считать мировым рекордсменом, в моем случае, т. к. в штат я был зачислен в столь преклонном возрасте (75 лет. – Г.Р. и др.)». С этой должности Мандельброт ушел в 2005 г., став, как уже отмечалось выше, Sterling Professor. Среди огромного числа его наград и почетных званий следует, наверное, назвать чрезвычайно престижные премии Александра Гумбольдта (Alexander von Humboldt Prize, 1988), Вольфа по физике (Wolf Prize, 1993), Японии (Japan Prize[10], 2003) и др. Он был академиком Национальной академии наук США (с 1987), Американской академии искусств и наук, Академии IBM технологии, почетным членом Норвежской академии наук и литературы, почетным доктором (Honoris causa) более 15 крупнейших университетов мира, в мае 2010 г. он был удостоен Почетной ученой степени Университета Джона Хопкинса (Балтимор [Baltimore, Maryland]). Мандельброт был награжден орденами и медалями многих стран (орденом Почетного легиона [Франция], медалью Президента Республики Италия, медалью Ричардсона [Lewis Fry Richardson Medal] Европейского геофизического общества и пр.).
Примеры фракталов различных систем
Свойство частей быть подобными всей структуре в целом называется самоподобием. Интервал самоподобия различных природных объектов может содержать масштабы от долей микрометра (при рассмотрении структуры пористых горных пород) до десятков километров (при рассмотрении рельефа местности и формы облаков). Примеры самоподобия можно найти в различных, на первый взгляд, объектах или процессах. Так, броуновское движение является хорошей иллюстрацией вероятностного самоподобия, в математике примерами самоподобия являются канторовы множества и функция Вейерштрасса, в музыке самоподообие связано с темперированным двенадцатитоновым строем Баха, русские деревянные матрешки, так же как китайские коробочки, – иллюстрации дискретного ограниченного самоподобия, акустические системы (в частности, основная мембрана внутреннего уха) также функционируют на основе принципа самоподобия; перечень самоподобных природных объектов и явлений можно продолжить, включив в него крону деревьев, гифы актиномицетов, разряд молнии, бронхиальное дерево, кровеносную и речную системы и т. д.; наконец, самоподобие часто присуще таким иерархическим структурам, как филогенетические деревья (см. рис. 3). Самоподобие предполагает, что копирование и масштабирование некоторого «эталонного» образа позволяют природе легко создавать сложную многомасштабную структуру.
Фрактальный анализ структуры экосистем
Рассмотрим видовую структуру сообщества. Зависимость видового богатства (S) от «выборочного усилия», выраженного через площадь обследованной территории (A) или объем выборки (N), давно интересовала исследователей. Здесь уместно привести слова Ю. Одума (1975, с. 196–197): «...подобрав уравнения для таких кривых (зависимости между числом видов и их обилием в различных местообитаниях. – Г. Р. и др.), можно помочь выяснить, какими математическими "законами" определяется зависимость между S и N».
Фракталы живой природы
| Радиолярия (рис. Э. Геккеля, 1902 г.) |
Кораллы | Сеть кровеносных сосудов сердца |
Фракталы неживой природы Фракталы технических систем

| Речная сеть | Молния | Дорожная сеть |
Фракталы в искусстве
| Ван Гог В. (Vincent Willem van Gogh, 1853–1890) «Звездная ночь. Сен Реми», 1889, Музей современного искусства, Нью-Йорк |
Ван Гог В. «Цветущий плодовый сад», 1888 г., Музей Ван Гога, Амстердам |
| Кацусика Хокусай (Hokusai Katsushika, 1760–1849) «Большая Волна в Канагаве», ок. 1831-1833; первая гравюра серии «36 видов горы Фудзияма»; Метрополитен-музей, Нью-Йорк; Британский музей, Лондон |
| Утагава [Андо] Хиросигэ (Utagawa [Ando] Hiroshige, 1797–1858) | |
| «Водовороты в проливе под мостом Конаруто», Государственный музей изобразительных искусств им. А. С. Пушкина, Москва | «Водовороты пролива Наруто в провинции Ава» (ок. 1820–1836); Британский музей, Лондон |
 |
В проливе Наруто между японскими островами Авадзи и Сикоку находится один из самых больших приливно-отливных водоворотов в мире. Скорость воды может доходить до 20 км/час, тогда диаметр воронки достигает 20 м. [http://nature.1001chudo. ru/japan_979.html, http://nature.1001chudo.ru/japan_ 979_gallery.html?show=wel-shikokugrjp.jpg]. |
| Храм Шри-Шива-Субраманья (Sri Siva Subramaniya temple) – самый большой индуистский храм Южного полушария (г. Нади, Фиджи)
|
Дали С. (Salvador Domènec Felip Jacint Dalí i Domènech, Marqués de Dalí de Púbol; 1904-1989)
«Лицо войны», 1940 г., Музей Бойманса-ван-Бёнингена, Роттердам, Нидерланды. Посещая Музей наук (Museu de la Ciencia) в Барселоне, Б. Мандельброт заметил его директору, что картина «Лицо войны» С. Дали дала ему «интуитивное понимание превосходства фрактальной геометрии, делая понятным всеобъемлющее сходство в формах природы» (Wagensberg, 2010, p. 37) |
Геометрический фрактал
| Логарифмическая спираль (гладкая самоподобная кривая; в углу – фрагмент раковины моллюска жемчужный кораблик [Nautilus pompilius]) |
Рис. 3. Примеры фрактальных структур
Еще в 1859 г. британский ботаник-любитель, эволюционист Х. Уотсон (Hewett Cottrell Watson, 1804–1881) предложил зависимость S от A для сосудистых растений Британии в билогарифмических координатах (цит. по: Pounds, Puschendorf, 2004):
lgS = lgc + zlgA, S = cAz,
где с и z – некоторые константы.
Другим исследователем, описавшим в 20-х годах ХХ в. зависимость S от A, стал шведский агрохимик и ботаник О. Аррениус (Olof Wilhelm Arrhenius, 1896–1977):
S/S1 = (A/A1)n ,
где S1 > S, A1 > A и n < 1 – константы (S – число видов, встреченных на площади А, S1 – число видов на площади A1). Фактически Аррениус «переоткрыл» уравнение Уотсона:
lgS = n(lgA – lgA1) + lgS1 = (lgS1 – nlgA1) + nlgA,
если c = S1/A1n и z = n. Таким образом, Аррениус попытался формализовать известное эмпирическое правило, согласно которому на большей площади обитает большее число видов, указав в качестве своих предшественников ботаников – швейцарца П. Жаккара (Paul Jaccard, 1868–1944) и финна Э. Палмгрина (Alvar Palmgren, 1880–1960).
Практически в это же время, резко критикуя уравнение Аррениуса (прямой подстановкой данных была продемонстрирована нереалистичность оценок, получаемых степенной зависимостью, предложенной Аррениусом для целого ряда видов растений), сходное уравнение предложил и американский ботаник Г. Глизон (Gleason, 1922) при описании зависимости в полулогарифмических координатах видового богатства от площади ареала для тополиных ассоциаций северного Мичигана (лог-линейная модель оценки видового разнообразия; см. табл. 1):
S = c + zlgA.
Таблица 1. Значение параметра z (species-area relationship, SAR) для различных местообитаний (по: Бигон и др., 1986 с изменениями)
| Местообитание | Диапазон значений |
| Произвольно выбранные участки материковой суши | 0.10 ÷ 0.16 |
| Океанические острова | 0.18 ÷ 0.37 |
| Изолированные местообитания | 0.17 ÷ 0.72 |
Степенные законы, описывающие зависимость видового богатства (S) от «выборочного усилия», выраженного через площадь обследованной территории (A), нашли свое логическое завершение в рамках равновесной теории островной биогеографии (MacArthur, Wilson, 1967).
Итак, основной вывод из этого краткого исторического экскурса состоит в том, что видовая структура сообщества самоподобна, что и отражает степенная зависимость числа видов от площади обследованной территории.
Главной количественной характеристикой фрактального объекта является его размерность. Наиболее просто понятие размерности можно ввести как количество переменных (или измерений), необходимых для полного описания положения точки в пространстве. Так, для описания положения точки на плоскости необходимо указать две координаты, поэтому плоскость, так же как и любая другая гладкая поверхность, имеет размерность, равную 2, то есть двумерна. Описать положение точки на линии можно с помощью одной координаты, поэтому линия одномерна, ее размерность равна 1. Аналогично размерность точки равна нулю, а пространство, в котором мы все живем, трехмерно. Введенное таким интуитивным образом понятие размерности соответствует тому, что в математике называется топологической размерностью (обозначается DT). Эта размерность всегда является целым числом.
Для фракталов же чаще всего характерна дробная[11], нецелая размерность. В соответствие с этим классическим подходом (размерность регулярных объектов) объект имеет n измерений, если его можно разбить на части гиперплоскостями, которые сами являются (n – 1)-мерными объектами. Таким образом, получается рекуррентное определение размерности: объемы – части пространства, поверхности – границы объемов, линии – границы поверхностей, а точки – границы линий; «промежутки» между целыми числами d следует «отдать» фрактальным (самоподобным) объектам (фрактальные размерности). «Самоподобию, в конце концов, все равно, целочисленный у нас показатель или нет» (Шредер, 2001, с. 165). Будем считать объект, который можно воспроизвести путем увеличения какой-либо его части, самоподобным, или инвариантным при преобразовании подобия, т. е. фракталом.
Фрактальность видовой структуры сообщества выражается в степенной зависимости между видовым богатством (S) и численностью сообщества (N, эквивалент масштаба):
S = N k , k = lnS / lnN, (1)
где 0 ≤ k ≤ 1 – предлагается Р. Маргалефом (1992, с. 143) рассматривать как индекс разнообразия: «...зависимость между S и N можно выразить следующим образом:
S = N 0 S = N k S = N 1
хемостат обычная экосистема музейная экспозиция
Степень k – прекрасный индекс разнообразия. Он находится в пределах между 0 и 1. Он может выражать связь с энергией (энергия, проходящая через систему, наибольшая в хемостате и нулевая в музее). Он не характеризует детали, но может выражать фрактальную самоорганизацию внутри системы».
Однако, как и любая фрактальная размерность, индекс k = (lnS) / (lnN) не дает исчерпывающего количественного представления о видовой структуре биотического сообщества: формула Маргалефа констатирует лишь сам факт наличия вида в выборке, но не содержит, например, сведений о распределении видов по численности или о степени их доминирования. Наиболее общее описание внутреннего устройства самоподобных объектов позволяет дать теория мультифракталов (основные понятия и положения этой теории были введены Б. Мандельбротом в начале 70-х годов прошлого века), характеризуемых бесконечной иерархией размерностей; она достаточно подробно изложена Е. Федером (1991) и Д. И. Иудиным (2006). Мультифракталы – неоднородные фрактальные объекты, для полного описания которых, в отличие от регулярных фракталов, недостаточно введения всего лишь одной величины (фрактальной размерности D), а необходим целый спектр таких размерностей, число которых, вообще говоря, бесконечно (это объясняется тем, что наряду с чисто геометрическими характеристиками, определяемыми величиной D, такие фракталы обладают и некоторыми статистическими свойствами).
Рассмотрим отличия монофрактального и мультифрактального подходов. Еще раз подчеркнем, что главной характеристикой фрактального множества является его размерность. Однако стандартная процедура определения фрактальной размерности не позволяет обнаружить различия между однородными и неоднородными (мультифрактальными) объектами. Для этого вводятся новые характеристики. При этом процедура определения размерности несколько усложняется: для каждой заполненной ячейки подсчитывается число содержащихся в ней точек, которое затем преобразуется в долю, где N – общее число точек. Далее используется полученный набор {pi}.
Пусть набор {pi = ni/N; ni – число особей i-го вида, N – размер пробной выборки, а i пробегает значения от единицы до полного числа видов S, обнаруженных в пробе} характеризует относительные частоты распределения особей по видам. Введем моменты распределения особей по видам и выясним характер их поведения при увеличении численности N:
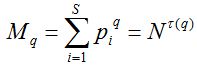 ,
,
где -∞ ≤ q ≤ ∞ называется порядком момента, а показатель τ характеризует скорость изменения соответствующего момента при увеличении размера выборки. Второе равенство в этом выражении характеризует масштабную инвариантность фрактального объекта (скейлинг), является обобщением формулы Маргалефа (1) и, очевидно, совпадает с последней при q = 0.
Обобщенной размерностью Реньи (Dq) распределения является убывающая функция q, вводимая определением (Федер, 1991):
![]() .
.
Обобщенные размерности Реньи не являются, строго говоря, фрактальными размерностями в общепринятом понимании этого слова. Поэтому наряду с ними используется так называемая функция мультифрактального спектра f(α), или «спектр сингулярностей». Для ее получения необходимо произвести преобразование Лежандра функции τ(q):
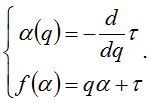
При применении мультифрактального формализма к структуре сообщества это сообщество рассматривается как множество, состоящее из отдельных фрактальных подмножеств, которые можно интерпретировать как совокупности особей, относящихся к видам со сходной представленностью. Для таких подмножеств можно вычислить фрактальную размерность, которая и будет характеризовать видовое разнообразие. Именно такой смысл имеет ордината точек α на графике мультифрактального спектра; абсцисса же точек f(α) характеризует относительную представленность (долю) видов того или иного подмножества (рис. 4). Наличие на графике спектра точек, лежащих по оси α («индекс сингулярности») близко к нулю (1), означает присутствие в сообществе сильных доминантов (причем, чем меньше абсцисса точек, тем сильнее доминирование – сообщество В); наличие же точек, лежащих близко к единице, означает присутствие в сообществе редких видов (2; сообщество А). Площадь под кривой спектра ∫f(α) можно интерпретировать как показатель, обратно пропорциональный выравненности видов в сообществе: чем она больше (сообщество А), тем меньше выравненность, и наоборот. Крайним вариантом выравненности является равнопредставленность видов; при этом весь спектр «схлопывается» в одну точку.
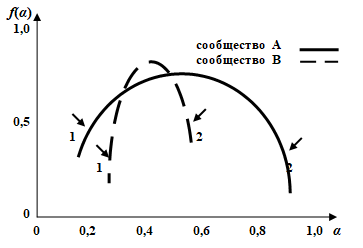
Рис. 4. Мультифрактальный спектр видовой структуры сообществ. По оси абсцисс отложен индекс сингулярности α, по оси ординат – значения функции мультифрактального спектра f(α)
Fig. 4. Multi-fractal spectrum of species structure of communities. On the X-axis is singularity index a, on the Y-axis is the values of the function of multi-fractal spectrum f(a)
На практике величины Dq можно оценить, используя несколько различающихся значений N, по более простой формуле:
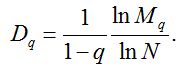
Примечательно, но факт: многие обобщенные размерности Реньи являются нормированными вариантами традиционных индексов видового разнообразия. Так, для q = 0 результат очевиден – это индекс Маргалефа-2:
![]()
Для q = 0.5,
![]()
где μ – индекс Животовского.
Можно показать, что для q = 1,
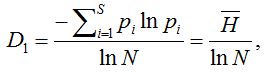
где – есть не что иное, как информационный индекс видового разнообразия Шеннона.
Для q = 2,
![]()
где с – индекс доминирования Симпсона – Джини. Этот ряд можно продолжить и получить весь спектр обобщенных размерностей Dq для любых q в интервале от
-∞ до +∞[12].
Мультифрактальный спектр видовой структуры сообщества (рис. 5) позволяет по-новому взглянуть на проблемы «индексологии». Действительно, используя для характеристики видовой структуры сообщества какой-либо индекс (пусть даже очень корректный), исследователь фактически описывает это сообщество одной точкой; фрактальный подход позволяет увидеть «портрет» сообщества в двухмерном пространстве {α, f(α)}. Естественно, что это открывает новые перспективы интерпретации экологической информации.

Рис. 5. Мультифрактальный спектр видовой структуры сообщества. Условные обозначения обобщенных фрактальных размерностей, соответствующих: ![]() – видовому разнообразию по Маргалефу (D0);
– видовому разнообразию по Маргалефу (D0); ![]() – видовому разнообразию по Шеннону (D1);
– видовому разнообразию по Шеннону (D1); ![]() – индексу доминирования по Симпсону (D2);
– индексу доминирования по Симпсону (D2); ![]() – доле редких видов (D-1)
– доле редких видов (D-1)
Fig. 5. Multi-fractal spectrum of species structure of a community. Conventional signs of generalized fractal dimentions corresponding to: ![]() – species diversity by Margalef (D0);
– species diversity by Margalef (D0); ![]() – species diversity by Shennon (D1);
– species diversity by Shennon (D1); ![]() – Simpson's index of domunance (D2);
– Simpson's index of domunance (D2); ![]() – fraction of rare species (D-1).
– fraction of rare species (D-1).
Флористический феномен Самарской Луки: фрактальная структура таксономического разнообразия
В качестве примера рассмотрим фрактальную структуру таксономического разнообразия по результатам исследования флоры Самарской Луки (Гелашвили и др., 2010б, 2011, 2013а).
Объект исследования
Самарская Лука представляет собой излучину Волги в среднем течении общей площадью свыше 1.5 тыс. км2 (Рощевский, 1996), образующую как бы полуостров. С трех сторон она ограничена акваториями Саратовского (долина Волги) и Куйбышевского (долина Волги и ее притока Усы) водохранилищ. Центральная и южная части полуострова уплощены, представляют собой пологонаклонное плато с абсолютными отметками от 150 до 200 м над уровнем моря, со слабым падением пластов с севера на юг, густо изрезанное многочисленными древними долинами. Северная часть представляет собой горный массив, известный под названием Жигули, или Жигулевские горы, где абсолютные отметки достигают 370 м над уровнем моря (Саксонов, 2006).
Знакомство с флорой Самарской Луки изумляет ботаников не только большим числом видов, населяющих эту территорию, но и разнообразным ее составом. Прежде всего это относится к группе эндемичных видов (в общем списке эндемиков разного ботанико-географического ранга – 102 вида), включающих редкую для равнинных флор подгруппу узколокальных эндемиков. Особую ценность природному комплексу Самарской Луки придают виды, классические места произрастания которых расположены здесь. Вряд ли какая-либо еще равнинная территория площадью немногим более 150 тыс. га сможет конкурировать с Самарской Лукой по плотности типовых территорий (по количеству новых для науки таксонов). В данное время выявлен 21 таксон, описанный по сборам с этой территории: 5 – в ранге вариаций и 16 – в ранге вида.
При разработке флористического районирования Самарской Луки основополагающим было принято ландшафтное районирование (Мельченко, 1991), т. к. оно учитывает литогенную основу, почвенный покров и биоту (Саксонов, 1996). На Самарской Луке выявлено семь элементарных флористических районов, границы которых совпали с соответствующими ландшафтами: Жигулевский (Ж), Винновский (Вин.), Александровский (А), Переволокско-Усинский (П.-У.), Шелехметский (Ш), Волжский (Вол.), Рождественский (Р). Главным критерием выделения элементарных флористических районов послужил анализ видового состава флоры Самарской Луки и особенности распространения некоторых ее элементов – эндемичных, реликтовых, редких и малочисленных видов (Саксонов, 1996). Согласно уровням организации флористических комплексов, уровню конкретной флоры или элементарному флористическому району соответствует уровень ландшафтной организации – ландшафт (Лукичева, Сабуров, 1969; Саксонов, 2006). Таким образом, можно предположить, что на территории Самарской Луки различаются семь конкретных флор. Количественная оценка степени различия флор с точки зрения их пространственного разнообразия была проведена с помощью параметра z Престона (Preston, 1962; Иванова и др., 2006). Престон теоретическим путем установил критическую или пороговую величину z = 0.27. При значении z > 0.27 сравниваемые флоры являются изолированными.
Анализ показал, что почти все районы Самарской Луки различны между собой настолько, что могут называться конкретными флорами. Не достигает названного числового порога лишь различие между Переволокско-Усинским и Александровским районами, причем разница между Переволокско-Усинским и Винновским достаточно велика (z = 0.35). Видимо, граница проходит через Александровский флористический район. Следовательно, на территории Самарской Луки можно наблюдать шесть районов, которые могут быть названы конкретными флорами.
Таким образом, Самарская Лука по флористической структуре представляет собой очень неоднородное образование. На ее территории только шесть флористических районов могут быть названы конкретными флорами. Седьмой флористический район – Александровский – представляет собой «пограничный» по отношению к соседним с ним Переволокско-Усинским и Винновским районам (Саксонов, 2006). Группы сухопутных и прибрежно-водных районов показывают между собой достаточную степень различия, чтобы называться изолятами, т. е. «экологическими сообществами с более или менее отчетливо выраженными границами» (Уилкокс, 1983, с. 117).
Правило Виллиса
Большинство авторов при анализе таксономического разнообразия опираются на правило (закон) Виллиса, аппроксимирующее взаимосвязь между числом таксонов и их объемом ранговым распределением (Willis, 1940; Майр, 1971; Численко, 1977; Кафанов, Суханов, 1981; Филиппов, 1984; Поздняков, 2005 и др.). Напомним, что ранговое распределение представляет собой преобразованный вектор численностей: наиболее обильной группе присваивается первый номер, следующей по численности группе – второй и так далее до наименее обильной группы, номер которой совпадает с общим числом анализируемых групп. Известно, что исторически ранговые распределения обычно связывают с именем итальянского экономиста и социолога В. Парето ([Vilfredo Pareto, 1848–1923]; т. н. принцип Парето). Принцип Парето гласит, что небольшая доля причин, вкладываемых средств или прилагаемых усилий, отвечает за большую долю результатов, получаемой продукции или заработанного вознаграждения. Часто принцип Парето называют принципом 80/20 (или, что не принципиально, 20/80). Действительно, 20% ассортимента продукции дают обычно 80% общего объема продаж в денежном выражении; 20 % преступников совершают 80 % преступлений; 80 % всех ложных тревог при срабатывании противоугонной сигнализации вызывается 20 % возможных причин и т. д. Принцип 80/20 говорит о том, что если мы изучим и проанализируем два набора данных, относящихся к причинам и результатам, то, скорее всего, мы получим картину несбалансированности. Численно этот дисбаланс может составлять 65/36, 70/30, 95/5 или принимать любые другие значения. При этом сумма двух чисел в подобных соотношениях не обязательно должна быть равна 100.
Широкую известность приобрел частный случай распределения Парето, изученный в 1949 г. профессором Гарвардского университета Дж. К. Ципфом [George Kingsley Zipf, 1902–1950], который показал, что если взять достаточно длинный текст или группу текстов (например, все пьесы Шекспира), то распределение слов в нем по частоте их встречаемости также подчиняется распределению Парето.
Распределение Парето, равно как и упоминаемые в литературе и отличающиеся деталями распределения Ципфа, Ципфа – Парето и Ципфа – Парето – Мандельброта, достаточно просто описывается математически. Так как в двойных логарифмических координатах оно представляет собой прямую, то, например, для модели распределения богатства среди населения отдельной страны уравнение можно записать в следующей форме:
lnM(i) = a – b × ln i,
где i – ранг социальной группы; M(i) – финансовые ресурсы, находящиеся в распоряжении этой группы; a и b – константы.
Потенцируя это выражение, получим уравнение
M(i) = A × i-b .
Величина A в этом уравнении есть доля богатства, находящегося в распоряжении первой по рангу группы. Величина b – тангенс угла наклона прямой – характеризует степень неравенства распределения богатств. При b → ∞ практически все национальное достояние находится в распоряжении первой по рангу группы. Если b → 0, то богатство примерно поровну распределено между всеми социальными группами. В экологии ранговые распределения под названием «кривые доминирования-разнообразия» по обилию того или иного вида характеризуют его успешность в конкуренции с другими видами за имеющийся в экосистеме ограниченный ресурс (Motomura, 1932; MacArthur, 1960; Рябко и др., 1978; Федоров, 1978). Теоретические модели, описывающие зависимость между числом видов и размером сообщества, также являются одной из форм представления видовой структуры сообщества. А. П. Левичем (1980) была показана эквивалентность всех этих типов описания видовой структуры, сформулировано правило экологической неаддитивности и разработан способ перевода ранговых распределений в зависимости числа видов в сообществе от числа организмов, названные функциями экологической неаддитивности.
В контексте таксономического разнообразия правило Виллиса связывает число таксонов и их объем, например, небольшое число родов представлено большим числом видов, тогда как большинство родов включают один-два вида (Willis, 1940; Численко, 1977; Кафанов, Суханов, 1981 и др.). Правило Виллиса в большинстве случаев справедливо для таких таксономических категорий, как виды, роды, отряды (порядки), тогда как для классов, типов и царств, в силу их малочисленности, подобные зависимости являются статистически некорректными. В качестве примера приведем зависимость «число родов – число видов» в билогарифмических координатах (рис. 6) из работы Willis (1940). В натуральных координатах графическая зависимость между числом таксонов и их объемом изображается т. н. вогнутой кривой систематиков, т. е. «распределением Парето или Ципфа», синонимом которым Мандельброт (2002) считает термин «асимптотически гиперболическое распределение».
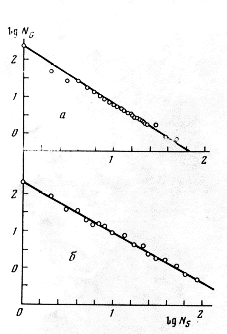
Рис. 6. Число родов NG в зависимости от содержащихся в них видов NS (по: Willis, 1940): а – семейство мареновых (Rubiaceae); б – семейство листоедов (Chrysomelidae); ось абсцисс – lg NS, ось ординат – lg NG (цит. по: Кафанов, Суханов, 1981).
Fig.6. The number of taxa NG depending on contained species NS ( by Willis, 1940): a - madder family (Rubiaceae); b - chrysomelid beetles (Chrysomelidae). X-axis - Lg NS, Y-axis - lg NG (quoted after Kofanov, Sukhanov, 1981)
Отношение специалистов к правилу Виллиса колеблется от категорического отрицания (Кафанов, Суханов, 1981) до сдержанного оптимизма с элементами фрактальной фразеологии (Поздняков, 2005). Рассмотрим эти крайние точки зрения подробнее. Критика правила Виллиса (Кафанов, Суханов, 1981, c. 349) сводится к отрицанию его биологического смысла, авторы полагают: «...тот факт, что результаты таксономических исследований удовлетворительно описываются законом Ципфа, свидетельствует, по нашему мнению, что объем надвидовых таксонов главным образом определяется соображениями удобства». К такому выводу авторы приходят, отталкиваясь от основной теоретической предпосылки в своей работе: «...учитывая таксономическую и информационную равноценность видов одного рода, количество информации h, содержащейся в данном роде, с точностью до линейных преобразований может быть аппроксимировано формулой Хартли (частный случай уравнения Шеннона): h = lnN, где N – число видов в роде».
Действительно, энтропия Хартли задает максимально возможную неопределенность в системе из N ячеек для двухбуквенного алфавита, равную N бит, при равной вероятности (p = const) их появления. Однако, если вероятности появления символов в сообщении не равновероятны, то для вычисления средней неопределенности используется информационная энтропия Шеннона. Вряд ли можно согласиться с мнением Кафанова и Суханова, что в «книге природы» частота встречаемости символов – «видов» – равновероятна. Следовательно, основной вывод авторов о субъективизме в обосновании объемов надвидовых таксонов базируется на некорректной исходной посылке.
Безусловно, более перспективным и продуктивным является высказанное А. А. Поздняковым (2005) предположение о фрактальности Естественной системы, понимаемой как упорядоченная совокупность таксонов. Естественная система, по мнению автора, представляет собой биологическое разнообразие, и с этим трудно не согласиться. К сожалению, попытка автора подвести под высказанный тезис некоторое теоретическое обоснование представляется неудачной. Дело даже не в отсутствии математического базиса, а, скорее, в эклектичности рассуждений о топологических и фрактальных размерностях.
Особо следует остановиться на работе Ю. Пузаченко и А. Пузаченко (1996), в которой авторы, по-видимому, первыми в отечественной литературе акцентировали внимание на аспектах самоподобия в контексте биоразнообразия на примере таксономической структуры классов Aves и Mammalia. К сожалению, эту попытку удачной назвать нельзя в силу следующих причин. Во-первых, непонятно, на базе каких мультифрактальных множеств авторы развивают декларированный ими «иконографический» подход. Семантика – это изучение смысла и значения конструкций формализованного языка теории. Для того чтобы говорить о мультифрактальности или хотя бы самоподобии конструкций формализованного языка, необходимо как минимум ввести соответствующую метрику. Авторы, однако, предлагают читателям лишь информационную меру, вообще говоря, далекую от семантики. Далее, отождествляя в пределе роста числа независимых реализаций два различных подхода к изучению семантики биоразнообразия – термостатистический (вольный авторский симбиоз понятий «термодинамический» и «статистический») и иконографический, авторы допускают существенную ошибку. Дело в том, что фрактальные структуры принципиально не являются и не могут являться состояниями термодинамического равновесия рассматриваемых систем. Они являются следствием сложнейшей нелинейной динамики открытых систем, где медленно изменяющаяся внешняя энергетическая накачка уравновешена процессами быстрой внутренней диссипации.
В рассматриваемом плане гораздо более продвинутыми являются работы В. Burlando (1990, 1993), которые, видимо, были незнакомы А. А. Позднякову. Б. Бурландо (Burlando, 1990) изучал ранговые распределения 44 списков видов, включающих следующие группы организмов: микроорганизмы, грибы, растения, насекомые, рыбы, амфибии, рептилии, птицы, млекопитающие. Как и требует правило Виллиса, распределения имели гиперболический вид в натуральных координатах и линейный характер с отрицательными наклонами в билогарифмических координатах. Он полагает, что значения наклонов (по модулю) соответствуют фрактальной размерности D таксономических групп, при этом значение размерности является характерным для разных таксономических групп (и групп разного систематического уровня). Так, значение размерности D больше для морских организмов по сравнению с наземными. Для позвоночных значение D выше, чем для беспозвоночных. При этом для морских рыб D > 2, в то время как птицы и млекопитающие имеют значения D = 1.66–1.67. Наконец, у амфибий и рептилий отмечены самые низкие значения фрактальной размерности D. При обсуждении этих результатов вполне уместно привести точку зрения Мандельброта (2002, с. 475) относительно асимптотически гиперболических распределений: «...данные, которыми нам приходится оперировать, представляют собой весьма разнородную смесь. Поэтому распределение данных является результатом совместного действия базового фиксированного "истинного распределения" и в высшей степени изменчивого "фильтра"… я отмечаю, что асимптотически гиперболические распределения с D < 2 очень "крепки" в этом смысле, т. е. многие самые разнообразные фильтры практически не изменяют их асимптотического поведения. С другой стороны, почти все прочие распределения таким свойством не обладают. Следовательно, гиперболическое истинное распределение можно наблюдать всегда: всевозможные наборы искаженных данных предполагают одно и то же распределение с одинаковым показателем D. При попытке применить тот же подход к большинству других распределений мы получим "хаотически" несовместимые результаты». Иными словами, практической альтернативой асимптотически гиперболическому распределению является не какое-то другое распределение, но «хаос». Таким образом, значение D < 2 является верификацией истинности гиперболической формы рангового распределения таксономического разнообразия.
Кроме того, по мнению Бурландо, значение D для разных таксономических категорий может служить отражением их эволюции. Так, высокое значение размерности D > 2 для морских рыб можно объяснить резким увеличением их таксономического разнообразия в кайнозое. У тетрапод более низкие значения D для амфибий и рептилий, по сравнению с птицами и млекопитающими, объясняются разными путями адаптивной радиации этих групп в постмезозойский период.
Несомненный интерес представляет применение фрактального подхода к анализу эволюционных процессов. Так, Бурландо (Burlando, 1993) при анализе таксономии ископаемых остатков, филогенетических систематик и сравнении разных уровней таксономической иерархии обнаружил, что частотное распределение субтаксонов в таксонах описывается гиперболической кривой, тем самым подтверждая фрактальную модель.
Рассмотрим результаты применения правила Виллиса к анализу таксономического разнообразия флоры Cамарской Луки, включающей 1302 вида сосудистых растений, принадлежащих к 505 родам (табл. 2). В данном случае речь идет об экстенсиональном (Buck, Hull, 1966) определении таксона родового ранга, т. е. эмпирическом определении объема таксона путем указания (перечисления) содержащихся в нем видов (табл. 3).
Таблица 2. Число родов и видов сосудистых растений в элементарных флористических районах Самарской Луки
| Элементарный флористический район |
Число родов | Число видов |
| Жигулевский (Ж) | 366 | 815 |
| Винновский (ВИН) | 357 | 778 |
| Александровский (АЛЕ) | 358 | 744 |
| Переволокско-Усинский (ПЕУ) | 323 | 654 |
| Шелехметский (ШЕЛ) | 240 | 460 |
| Рождественский (РОЖ) | 355 | 731 |
| Волжский (ВОЛ) | 276 | 531 |
| Самарская Лука в целом | 505 | 1302 |
Таблица 3. Количественные соотношения таксономических категорий видового и родового рангов сосудистых растений Самарской Луки
| Категории | Число таксонов | |||||||||||||||||
| Род | 1 | 1 | 1 | 1 | 3 | 3 | 2 | 4 | 4 | 3 | 9 | 9 | 8 | 14 | 34 | 43 | 98 | 267 |
| Вид | 41 | 19 | 17 | 16 | 15 | 14 | 13 | 12 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
Для флоры Самарской Луки зависимость между числом таксонов и их объемом удовлетворительно описывается степенной функцией, график которой имеет вид «вогнутой кривой систематиков» в обычных и билогарифмических координатах (рис. 7), подтверждая справедливость правила Виллиса (ср. с рис. 6). Заметим, что формально указанные выше зависимости не являются ранговыми распределениями в каноническом виде, поскольку по оси абсцисс отложены не ранги, а число видов, входящих в тот или иной род. Для построения ранговых зависимостей преобразуем данные табл. 3 таким образом, что наиболее обильный род Carex, состоящий из 41 вида, получает первый ранг и т. д. (табл. 4). Полученные ранговые распределения в натуральных и полулогарифмических координатах также не противоречат правилу Виллиса (рис. 8).
Таблица 4. Ранговое распределение числа родов (NG) сосудистых растений Самарской Луки по числу входящих в них видов (NS)
| Номер ранга рода | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| NS | 41 | 19 | 17 | 16 | 15 | 14 | 13 | 12 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
Не вдаваясь в подробности биологической содержательности ранговых распределений, рассмотренных ранее разными авторами, отметим, что, несмотря на широкое применение, метод ранговых распределений достаточно уязвим с точки зрения статистической обоснованности. Н. Г. Булгаков с соавторами (2003) весьма подробно анализирует pro et contra применения ранговых распределений в их каноническом виде.
Основные замечания и претензии сводятся к следующему. На каком основании первый ранг приписывается наиболее обильной группе? Более естественным явилось бы ранжировать группы по возрастанию их обилия, как это принято при построении ранговых статистик. Кроме того, поскольку ранги откладывают по оси абсцисс, то в силу устойчивой математической традиции это означает, что ранг рассматривается как независимая переменная, а обилие соответствующей группы – как зависимая переменная. Однако очевидно, что ранг определяется самим исследователем в зависимости от обилия группы. Наконец, более серьезные претензии могут быть предъявлены к правомерности применения регрессионного анализа для получения уравнения связи между обилием группы и его рангом. Одно из требований к переменным, предусмотренное теорией регрессионного анализа, заключается в том, что независимая переменная должна быть детерминированной и непрерывной величиной, что не выполняется для дискретных рангов. К сожалению, нельзя не согласиться с выводом авторов, что в подавляющем большинстве случаев применения регрессионного анализа к экспериментальным данным экологических исследований теоретические требования к переменным не выполняются. Подводя итог критическому анализу ранговых распределений (Булгаков и др., 2003, с. 168), авторы подчеркивают, что «ранговые распределения в их традиционной форме являются, по сути, обычными эмпирическими функциями распределения, только построенными, так сказать, "задом наперед"».
а
б
Рис. 7. Зависимость числа родов (NG) сосудистых растений Самарской Луки от числа содержащихся в них видов (NS) в натуральных (а) и билогарифмических (б) координатах
Fig.7. Dependence of taxa number (NG) of vascular plants of Samarskaya Luka on the number of contained species (NS) in natural (a) and log-log (b) coordinates
а
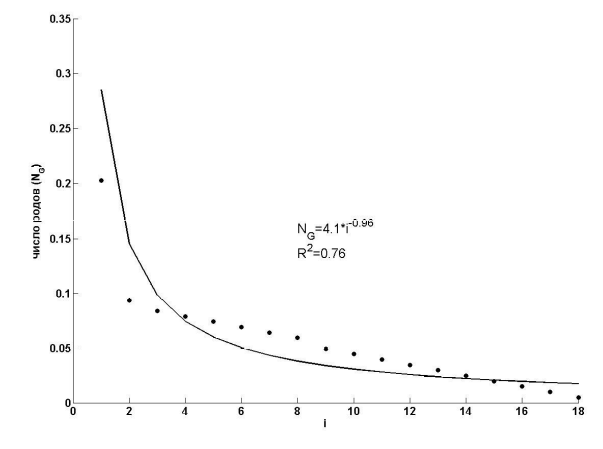
б

Рис. 8. Ранговое распределение числа родов (NG) сосудистых растений Самарской Луки в зависимости от числа содержащихся в них видов (NS) в натуральных (а) и полулогарифмических (б) координатах (i – номер ранга)
Fig. 8. Rank distribution of taxa number (NG) of vascular plants of Samarskaya Luka depending on the number of contained species (NS) in natural (a) and semilogarithmic (b) coordinates ( i - rank number)
Ранговые распределения и «вогнутые кривые систематиков» фиксируют лишь «статический таксономический портрет» сообщества и не дают ответа на вопрос: как будет изменяться число родов по мере того, как в сообществе будут находиться (встречаться) новые виды? Напомним, что в рамках экстенсиональной характеристики таксона его объем фактически ограничивается лишь теми видами, которые реально известны систематику (Шаталкин, 1995). В то же время выяснение закономерности, которой подчиняется рост числа родов при увеличении числа видов, т. е. «динамический таксономический портрет», может оказаться полезным при анализе структурно-функциональной организации сообщества, в том числе и в прогностическом плане.
Список публикаций к настоящей статье однозначно свидетельствует о том, что признание фрактальной организации видовой структуры биотического сообщества можно считать свершившимся фактом (Гелашвили и др., 2007в, 2008в, 2009а, 2010б, 2013а, б; Якимов и др., 2014б, Yakimov et al., 2014 и др.). С физической точки зрения это вполне естественно, поскольку сильно неравновесные системы, так или иначе связанные переносом интенсивных потоков вещества, энергии, заряда, обладают имманентной структурной универсальностью и являются фракталами. Потоки энергии и вещества, проходящие через открытые системы, обеспечивают возникновение в них эффектов самоорганизации – образования макроскопических диссипативных структур. Эти структуры очень часто демонстрируют в широком диапазоне параметров пространственно-временной скейлинг – свойство самоподобия или масштабной инвариантности – один из фундаментальных видов симметрий физического мира, играющих формообразующую роль во Вселенной. Пространственно-временной скейлинг характеризуется сильными, спадающими по степенному закону, корреляциями, которые типичны для критических явлений. Поэтому качественно динамика подобных систем производит впечатление самоорганизованного и самонастраивающегося критического режима. Явления такого рода были объединены недавно общим наименованием систем с самоорганизованной критичностью (self-organized criticality; Bak et al., 1988). Самоорганизованная критичность соединяет в себе два направления современной физической парадигмы – самоорганизацию и критические явления, и актуализирует новый подход к анализу сложного поведения нелинейных распределенных систем. Этот новый подход связывает динамику критических флуктуаций с появлением фракталов в конфигурационном пространстве нелинейной распределенной системы при кинетическом фазовом переходе. Все это в полной мере относится к биоэкологическим системам (Иудин, 2006). Более того, постановка вопроса о фрактальной структуре биотического сообщества является вполне логичной и в контексте дискуссии о видовом насыщении сообществ (Джиллер, 1988; Бигон и др., 1989 др.). Именно степенной закон, не предполагающий насыщения функции f(x), учитывает вклад редких видов, или видов с «единичной численностью» (Rozenzweig, 1975), не противоречит «правилу экологической неаддитивности» (Левич, 1980) и, наконец, дает возможность применить фрактальный формализм для характеристики видовой структуры сообщества.
Мы полагаем, что вышеприведенная точка зрения относительно фрактальной природы видового разнообразия биотического сообщества в полной мере относится и к «таксономическому разнообразию», поскольку последнее должно реально отражать природную структурную иерархию биологических систем разного ранга, т. е. уже упоминавшуюся Естественную систему (Поздняков, 2005). Однако, в отличие от Позднякова (2005), опирающегося при обосновании Естественной системы как фрактала на структурное подобие, выражающееся в ранговых распределениях таксонов по их объему либо дифференциальных признаков по частоте их использования, а также других авторов, использующих косвенную аргументацию (Burlando, 1991, 1993; Ю. Пузаченко, А. Пузаченко, 1996), мы намерены продемонстрировать прямые доказательства фрактальной структуры таксономического разнообразия на основе классических представлений фрактальной геометрии и мультифрактального анализа (Федер, 1991; Мандельброт, 2002; Иудин, 2006).
Фрактальный анализ таксономического разнообразия флоры Самарской Луки
При знакомстве с фракталами центральной оказывается формообразующая идея самоподобия, суть которой сводится к репликации фрагмента структуры в ее целое при воспроизведении свойств целого в каждом фрагменте. Ранее нами были разработаны методологические основы фрактальной теории видовой структуры сообщества (Гелашвили и др., 2013а, б), что позволило адаптировать существующий математический аппарат и логику обоснований для анализа фрактальной структуры таксономического разнообразия. С математической точки зрения фрактальный объект оказывается инвариантным (демонстрирует скейлинг, или масштабную инвариантность) относительно масштабных изменений (растяжений и сжатий) пространства. Так, например, при фрактальном анализе видовой структуры сообщества математическим выражением этого факта (скейлинга) является степенная зависимость числа видов (S) от численности (N) сообщества
S = Nk, k = lnS / lnN, (2)
где 0 ≤ k ≤ 1 предлагается Маргалефом (1992) рассматривать как индекс разнообразия. Выражение (1) эквивалентно утверждению о самоподобии системы. Оно показывает, что структура сообщества инвариантна относительно преобразования его численности, выступающей в данном случае эквивалентом масштаба. Следует отметить, что все алгоритмы расчета фрактальной размерности основаны на степенных законах. Такого рода зависимости характерны для фракталов и являются математическим выражением их свойства самоподобия. Однако это свойство у реальных природных фракталов выполняется лишь на некотором конечном характерном диапазоне масштабов, вне этого диапазона самоподобие и фрактальные свойства пропадают.
Для таксономического разнообразия, рассматриваемого в координатах «число родов, NG» – «число видов, NS», зависимость (2) может быть записана в виде:
NG = NSk, k = lnNG / lnNS.
При этом все вышеприведенные рассуждения остаются в силе, и число видов (NS) в данном случае также является эквивалентом масштаба.
Рассмотрим этот вопрос подробнее. Нас интересует, насколько структура таксономического разнообразия инвариантна относительно преобразования его масштаба, выражаемого через рост числа видов. Для решения этого вопроса воспользуемся данными табл. 3 и преобразуем их для построения кумулятивной кривой зависимости накопления числа родов при кумулятивном накоплении числа видов (см. табл. 4), что в рассматриваемом контексте эквивалентно увеличению масштаба. Алгоритм кумулятивного накопления родов или видов прост. Например, очевидно, что «накопленное» число одно- и двувидовых родов равно их сумме – 365, при этом в состав этих родов входит 463 вида (табл. 5). График зависимости «число родов, NG» – «число видов, NS» (см. рис. 4) удовлетворительно аппроксимируется степенным законом, как в натуральных, так и в билогарифмических координатах. Показатель k = 0.377 можно трактовать как соответствующую фрактальную размерность: число элементов таксономического разнообразия (родов) меняется по степенному закону с дробным показателем k при увеличении размеров системы, т. е. с ростом числа видов. Этот факт указывает, что процесс роста числа родов есть процесс самоподобный, а следовательно, проявляет свойства фрактала.
Таблица 5. Накопление числа родов сосудистых растений Самарской Луки при увеличении видового богатства
| А | 267 | 463 | 592 | 728 | 798 | 864 | 909 | 981 | 1008 | 1048 | 1096 | 1122 | 1164 | 1209 | 1225 | 1242 | 1261 | 1302 |
| Б | 267 | 365 | 408 | 442 | 456 | 464 | 473 | 482 | 485 | 489 | 493 | 495 | 498 | 501 | 502 | 503 | 504 | 505 |
| В | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 13 | 14 | 15 | 16 | 17 | 19 | 41 |
Примечание. А – кумулятивное накопление видов; Б – кумулятивное накопление родов; В – число видов в роде.
Следует подчеркнуть, что рассмотренные выше примеры и теоретические положения использованы для характеристики только одного из компонентов таксономического разнообразия – числа родов. Соответствующим математическим образом являются т. н. монофракталы, т. е. множества, характеризующиеся единственным параметром – фрактальной размерностью. В рассматриваемом примере показатель k соответствует фрактальной размерности, применяемой при описании т. н. регулярных фракталов. В рамках такого описания роли отдельных родов в формировании таксономического разнообразия нивелированы: зависимость фиксирует лишь факт наличия того или иного рода в выборке, игнорируя его объем, т. е. наполненность видами.
Вместе с тем сама по себе фрактальная размерность не дает исчерпывающего количественного представления о структуре самоподобного объекта: множества с одинаковой фрактальной размерностью могут иметь различную структуру. В реальности мы имеем дело с принципиально неоднородным распределением видов по родам анализируемой выборки, что и констатирует правило Виллиса. Для учета гетерогенности таксономического разнообразия необходим переход от анализа числа родов к анализу их относительных представленностей видами и, соответственно, от монофрактального анализа к мультифрактальному.
Это обстоятельство указывает на необходимость использования теории мультифракталов – неоднородных фрактальных объектов, для полного описания которых, в отличие от регулярных фракталов, недостаточно введения всего лишь одной величины, его фрактальной размерности, а необходим целый спектр таких размерностей, число которых, вообще говоря, бесконечно.
a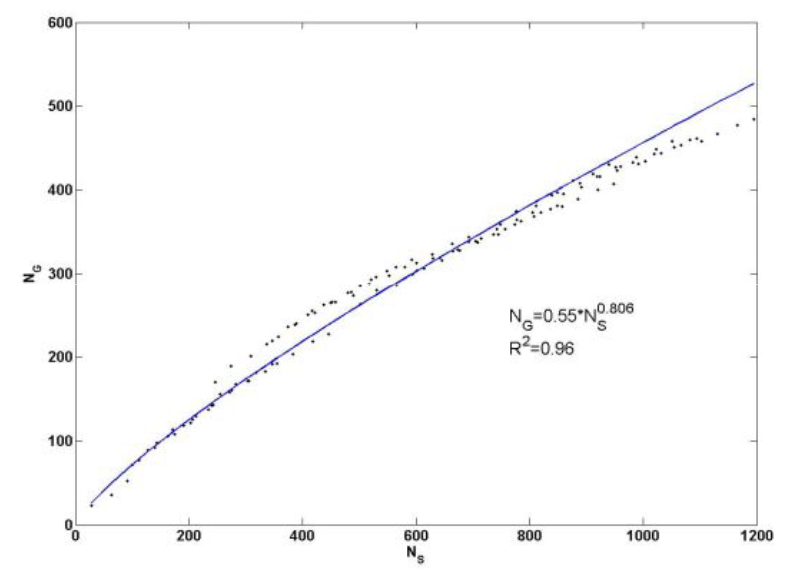
б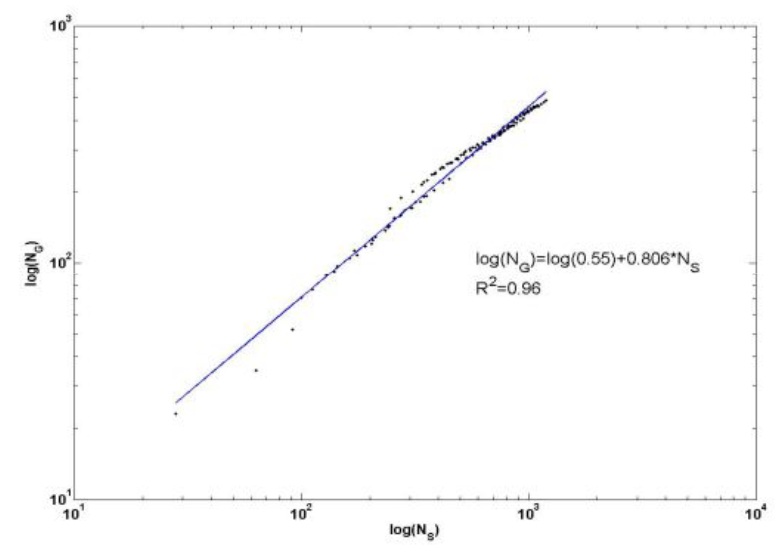
Рис. 9. Графики накопления числа родов сосудистых растений Самарской Луки при увеличении видового богатства в натуральных и билогарифмических координатах
Fig. 9. Graph of accumulation of taxa number of vascular plants of Samarskaya Luka in increasing species richness in natural and log-log coordinates
Пусть набор {pi} характеризует относительные частоты распределения видов по родам: pi = ni/NS, где ni – число видов i-го рода, NS – общее число видов в выборке, а i пробегает значения от единицы до полного числа видов NS, обнаруженных в выборке. Введем моменты распределения видов по родам и выясним характер их поведения при увеличении численности NS:
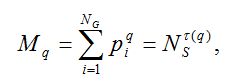 (3)
(3)
где -∞ ≤ q ≤ +∞ называется порядком момента, а показатель τ характеризует скорость изменения соответствующего момента при увеличении размера выборки.
Второе равенство в выражении (3) характеризует масштабную инвариантность фрактального объекта (скейлинг).
Для построения мультифрактального спектра таксономического разнообразия сначала необходимо проверить гипотезу о степенном характере скейлинга. Для этого рассмотрим, как ведут себя моменты Mq при асимптотическом увеличении числа видов.
В табл. 6 приведены данные, необходимые для построения матрицы моментов. Исходно мы имеем данные по числу видов в родах для 7 флористических районов, рассматриваемых как выборки, или пробы. Для построения адекватного спектра этого числа выборок недостаточно, поэтому применяется следующая процедура. К исходному числу проб (флористических районов) мы добавляем пробы, полученные в результате суммирования комбинаций исходных проб. Комбинации составлялись исходя из сходства флористических районов. Анализ сходства (рис. 10) приведен в работе (Иванова и др., 2006) и основан на показателе Престона (Preston, 1962).
Таким образом, в дополнение к 7 исходным пробам мы получаем еще 6 дополнительных: [3 4] [5 7] [5 7 6] [2 3 4] [1 2 3 4] [1 2 3 4 5 6 7]. Следующий шаг: вычисление набора моментов Mq (-6 ≤ q ≤ +6) для каждой пробы (рис. 11). Значения наклонов графиков Mq(N) составляют вектор τ(q).
Обобщенной размерностью Dq (обобщенной размерностью Реньи) распределения является убывающая функция q, вводимая определением (Федер, 1991):
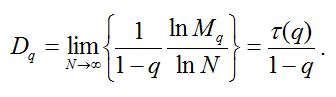
Таблица 6. Данные по распределению видов по выборкам
| Род | Номера элементарных
флористических районов*, составивших пробу |
Номера элементарных
флористических районов, вошедших в объединенную пробу |
||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | [5 7] | [1 2 3 4] | [1 2 3 4 5 6 7] | Общее число видов | ||||
| 1 | Equisetum | 3 | 1 | 0 | 0 | 1 | 0 | 0 | … | 1 | … | 4 | 5 | 5 |
| 2 | Hippochaete | 2 | 0 | 0 | 0 | 0 | 0 | 0 | … | 0 | … | 2 | 2 | 2 |
| 3 | Asplenium | 0 | 0 | 0 | 1 | 0 | 0 | 1 | … | 1 | … | 1 | 2 | 2 |
| 4 | Botrychium | 0 | 0 | 0 | 0 | 1 | 0 | 0 | … | 1 | … | 0 | 1 | 1 |
| 5 | Dryopteris | 1 | 1 | 1 | 0 | 0 | 0 | 0 | … | 1 | … | 3 | 3 | 3 |
| 6 | Polystichum | 0 | 0 | 0 | 0 | 0 | 0 | 1 | … | 1 | … | 0 | 1 | 1 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 500 | Parietaria | 0 | 0 | 0 | 0 | 0 | 0 | 1 | … | 1 | … | 0 | 1 | 1 |
| 501 | Urtica | 0 | 3 | 0 | 0 | 0 | 0 | 1 | … | 1 | … | 3 | 4 | 4 |
| 502 | Valeriana | 0 | 2 | 0 | 0 | 1 | 0 | 0 | … | 1 | … | 2 | 3 | 3 |
| 503 | Viburnum | 0 | 1 | 0 | 0 | 0 | 0 | 0 | … | 0 | … | 1 | 1 | 1 |
| 504 | Viola | 0 | 5 | 0 | 0 | 2 | 1 | 3 | … | 6 | … | 5 | 11 | 11 |
| 505 | Parthenocissus | 0 | 1 | 1 | 0 | 0 | 0 | 0 | … | 0 | … | 3 | 2 | 2 |
| Число видов в пробе | 63 | 502 | 246 | 28 | 143 | 100 | 112 | … | 565 | … | 983 | 1302 | 1302 | |
Примечание. * 1 – Жигулёвский район; 2 – Винновский район; 3 – Александровский район; 4 – Переволокско-Усинский район; 5 – Шелехметьевский район; 6 – Рождественский район; 7 – Волжский район.
Рис. 10. Сходство флористических районов Самарской Луки
Fig.10. Similarity of floristic areas of Samarakaya Luka
Рис. 11. График поведения моментов Mq при росте числа видов
Fig.11. Graph of behavior of moments MQ in increasing the number of species
Примечательно, что многие обобщенные размерности Реньи являются нормированными вариантами традиционных индексов видового разнообразия (об этом говорилось и в первой лекции (Розенберг, 2007)). Обобщенные размерности Реньи не являются, строго говоря, фрактальными размерностями в общепринятом понимании этого слова. Поэтому наряду с ними используется так называемая функция мультифрактального спектра f(α), или «спектр сингулярностей». Для ее получения необходимо произвести преобразование Лежандра функции τ(q):
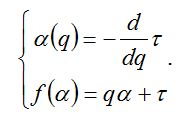
При применении мультифрактального формализма к анализу таксономического разнообразия на уровне родов («родовое разнообразие») совокупность таксонов родового ранга рассматривается как множество, состоящее из отдельных фрактальных подмножеств, которые можно интерпретировать как совокупности родов определенного объема. Для таких подмножеств можно вычислить фрактальную размерность, которая и будет характеризовать родовое разнообразие. Именно такой смысл имеет ордината точек на графике мультифрактального спектра. Абсцисса же точек характеризует относительный объем рода того или иного подмножества. Наличие на графике спектра точек, лежащих по оси «а» («индекс сингулярности») близко к нулю, означает присутствие в изучаемой таксономической совокупности доминантов (таксонов родового ранга с наибольшей видовой представленностью), причем, чем меньше абсцисса точек, тем сильнее доминирование. Наличие точек, лежащих на оси «а» близко к единице, означает присутствие в изучаемой таксономической совокупности родов с малой видовой представленностью (по аналогии с редкими видами).
Площадь под кривой спектра можно интерпретировать как показатель, обратно пропорциональный выравненности родов по относительному объему: чем она больше, тем меньше выравненность, и наоборот.
На рис. 12 представлен мультифрактальный спектр таксономического разнообразия сосудистых растений Самарской Луки.
Спектр «1» – мультифрактальный спектр родовой структуры растительного сообщества Самарской Луки. Сообщество характеризуется высокой долей одно- и двувидовых родов (238 и 100 соответственно).
Проведем следующую операцию: для всех родов, число видов в которых больше 2, заменим число содержащихся в них видов на произвольное число в интервале от 1 до 4. Таким образом, произойдет увеличение общей выравненности сообщества и исчезнут рода с много большим, чем у основной массы, числом видов. На графике спектров (см. рис. 12) этому случаю соответствует спектр «2». При этом левая ветвь спектра сокращается и поднимается вверх. Можно показать, что дальнейшее увеличение выравненности приведет к вырождению спектра в точку. Таким образом, левая ветвь спектра соответствует родам, содержащим большое число видов (т. е. доминирующим родам). Выравненность в выборке увеличилась в силу того, что теперь диапазон значений числа видов в роде находится в интервале [1, 4] (в исходной выборке интервал [1, 40]). На увеличение выравненности в сообществе спектр реагирует уменьшением площади под кривой.
Проведем обратную операцию: для всех родов, число видов в которых меньше или равно 2, заменим число содержащихся в них видов на произвольное число от 1 до 5. Тем самым мы «увеличиваем» разнообразие в сообществе, частично «избавляясь» от одно- и двувидовых родов. На графике спектров этому случаю соответствует спектр «3». Спектр реагирует на такое изменение структуры удлинением правой ветви. Следовательно, правая ветвь спектра соответствует родам, содержащим малое число видов. И чем она короче и выше, тем большее количество таких родов содержится в сообществе. Площадь под кривой сократилась, но, в отличие от предыдущего случая, увеличение выравненности произошло за счет удаления «перекоса» в сторону одно- и двувидовых родов.
Рис. 12. Мультифрактальный спектр таксономического разнообразия сосудистых растений Самарской Луки
Fig. 12. Multi-fractal spectrum of taxonomic diversity of vascular plants of Samarskaya Luka
| [1] Самое высокое ученое звание в Йельском университете, присуждается с 1920 г. Джон Уильям Стерлинг (John William Sterling; 1844–1918) был адвокатом и филантропом; он завещал свое состояние Йельскому университету ($18 млн, которые в 2003 г. «превратились» в $180 млн). На эти средства построена библиотека, химическая лаборатория, факультеты правоведения, богословия, школа медицины и пр.
[2] Один из них был парижским математиком, членом группы, известной под общим псевдонимом «Николя Бурбаки [Bourbaki Nicolas]», которая выступала с концепцией построения математики с точки зрения принципов логики и аксиоматики теории множеств. [3] Интересный факт: грант Рокфеллерского фонда (A maverick’s apprenticeship..., 2004) по рекомендации фон Неймана был устроен У. Уивером [Warren Weaver], который с 1932 г. более 20 лет возглавлял отдел естественных наук этого Фонда и как менеджер науки способствовал поддержке наиболее талантливой молодежи. Достаточно часто информационный индекс разнообразия называют индексом Шеннона – Уивера, хотя в совместной работе с К. Шенноном [Claude E. Shannon] над книгой «Математическая теория связи», Уивер «отвечал» за философско-методологическое обоснование построений Шеннона (см.: (Розенберг, 2010)). Еще одна «точка пересечения», в которой «встретились» видовая структура сообществ и фракталы… [4] Правда, англоязычные исследователи ведут свой «отсчет» от перевода этой работы на английский язык (Mandelbrot, 1977). [5] «Дайте чудовищу какое-нибудь уютное, домашнее имя, и вы удивитесь, насколько легче будет его приручить!» (Мандельброт, 2002, с. 18). [6] Хотя, чего тут непривычного? Любые усреднения «уходят» от изначальной целочисленности исходных значений. Например, «По данным ЦРУ США, в среднем женщины в России рожают 1,39 ребенка» (Газета «Ведомости», 22 ноября 2007 г.) или детская классика Самуила Маршака – стихотворение «Про одного ученика и шесть единиц»: – Задачу задали у нас. Её решал я целый час, И вышло у меня в ответе: Два землекопа и две трети. [7] Приведем еще одну цитату из работы Н. Г. Макаренко (2002, с. 122): «Позднее оказалось, что фракталами являются и давно известные в анализе нерегулярные функции, вызывавшие отвращение аналитиков прошлого века». Подтверждением тому служат слова из письма 20 мая 1893 г. французского математика Ш. Эрмита [Charles Hermite, 1822–1901] – нидерландскому математику Т. Стилтьесу [Thomas Johannes Stieltjes, 1856–1894], которые также приводит Макаренко: «С омерзением и ужасом я отворачиваюсь от этой зловредной язвы – непрерывных функций, нигде не имеющих производных…». Мандельброт (2002, с. 61) так цитирует эти же слова: «Это наказание Господне, эти жалкие функции без производных…». [8] Мандельброт приводит такую аналогию (In his own..., 1985): «Соревнование важно в жизни, следовательно, и в науке; но почему наука должна подражать спорту, где гонку на милю и 1500 метров (только на 7.3 % короче!) часто выигрывают разные чемпионы? И хуже того, в то время как десятиборье является Олимпийской дисциплиной, "научное десятиборье", которое я, казалось, практиковал, не приветствовалось в академии». [9] За всю историю компании IBM («Голубого Гиганта») этого звания были удостоены чуть более 200 специалистов. [10] Эта в высшей степени престижная международная премия учреждена Фондом науки и технологий Японии. Она вручается в присутствии императора ежегодно в двух областях за «оригинальные и выдающиеся достижения, способствующие прогрессу науки и технологий и продвижению человечества к миру и процветанию». [11] Понятие дробной размерности на первый взгляд может показаться абсурдным, однако при работе с фрактальными объектами оно совершенно необходимо, и литература изобилует множеством примеров, ставших хрестоматийными (Федер, 1991; Пайген, Рихтер, 1993). Заметим, что математикам давно известны эти представления, и нецелые размерности и некоторые основные свойства фрактальных объектов изучались начиная с XIX в. [12] В частности, В. Н. Якимов (2007) приводит пример обобщенной размерности Реньи для q = –1, где и наибольший вклад в значение величины момента М-1 вносят именно редкие виды. |
Заключение
Таким образом, можно утверждать, что закономерности, выявленные ранее для мультифрактального спектра видовой структуры сообщества (Гелашвили и др., 2013a), в известной мере сохраняются и для спектра родовой структуры. Другими словами, в пространстве {pi}, характеризующих относительные частоты распределения видов по родам, мультифрактальный спектр представляет собой обобщенный геометрический образ родовой структуры таксономического разнообразия.
Напомним, что в рамках фрактальной методологии нас интересовал вопрос, насколько структура таксономического разнообразия (в данном случае – родовой структуры) инвариантна относительно преобразования его масштаба, выражаемого через рост числа видов. В то же время, А. А. Поздняков (2003, с. 62) приводит точку зрения А. Виганда и Ю. А. Филипченко, согласно которой «увеличение количества видов в результате видообразования еще не означает появление нового рода, т. е. "природа" видов и родов различна и роды не могут возникать из видов». Не вдаваясь в детали дискуссии по этому вопросу, отметим, что вне зависимости от того, как идет процесс образования новых родов во времени (на эволюционном масштабе), на любом временном срезе таксономическое разнообразие должно иметь самоподобный, или фрактальный, характер.
Библиография
Азовский А. И., Чертопруд М. В. Анализ пространственной организации сообществ и фрактальная структура литорального бентоса // Докл. Академии наук (ДАН). 1997. Т. 356. № 5. С. 713–715.
Азовский А. И., Чертопруд М. В. Масштабно-ориентированный подход к анализу пространственной структуры сообществ // Журн. общ. биол. 1998. Т. 59. № 2. С. 117–136.
Беклемишев В. Н. Об общих принципах организации жизни // Бюл. МОИП. Отд. биол. 1964. Т. 69. Вып. 2. С. 22–38.
Бигон М., Харпер Дж., Таунсенд К. Экология: Особи, популяции, сообщества : В 2 т. М.: Мир, 1989. Т. 1. 667 с.; Т. 2. 477 с.
Булгаков Н. Г., Левич А. П., Максимов В. Н. Региональный экологический контроль на основе биотических и абиотических данных мониторинга // Экологический мониторинг. Методы биологического и физико-химического мониторинга. Ч. V. Н. Новгород: Изд-во ННГУ, 2003. C. 93–259.
Гелашвили Д. Б., Дмитриев А. И., Иудин Д. И., Розенберг Г. С., Солнцев Л. А. Мультифрактальный анализ видовой структуры сообществ мелких млекопитающих Волго-Уральского палеоценоза // Докл. Академии наук (ДАН). 2008а. Т. 421. № 4. С. 562–566.
Гелашвили Д. Б., Иудин Д. И., Розенберг Г. С. Фрактальная структура перколяционного кластера и пространственное распределение доминантных видов // Докл. Академии наук (ДАН). 2006a. Т. 408. № 4. С. 560–563.
Гелашвили Д. Б., Иудин Д. И., Розенберг Г. С., Снегирёва М. С., Солнцев Л. А., Федюнин В. А., Якимов В. Н. Фрактальная характеристика видовой структуры сообществ наездников-ихневмонид Среднего Урала // Докл. Академии наук (ДАН). 2010а. Т. 434. № 6. С. 838–841.
Гелашвили Д. Б., Иудин Д. И., Розенберг Г. С., Солнцев Л. А., Иванова И. О. Биоразнообразие и климат с позиции теории фракталов // Изв. СамНЦ РАН. 2007а. Спец. выпуск «ELPIT-2007». Сер. «Экология». С. 139–150.
Гелашвили Д. Б., Иудин Д. И., Розенберг Г. С., Солнцев Л. А., Иванова И. О. Биоразнообразие и климат с позиции теории фракталов // Сб. тр. Первого междунар. экологического конгресса (третьей междунар. научно-техн. конф.) «Экология и безопасность жизнедеятельности промышленно-транспортных комплексов» ELPIT 2007. (20–23 сентября 2007 г., Тольятти, Россия). Т. 1. Тольятти: ТолГУ, 2007б. С. 214–219.
Гелашвили Д. Б., Иудин Д. И., Розенберг Г. С., Солнцев Л. А., Якимов В. Н. Мультифрактальные структуры в биоэкологии // Нелинейный мир. 2008б. Т. 6. № 11–12. С. 697–703.
Гелашвили Д. Б., Иудин Д. И., Розенберг Г. С., Якимов В. Н. Степенной характер накопления видового богатства как проявление фрактальной структуры биоценоза // Журн. общ. биол. 2007в. Т. 68. № 3. С. 170–179.
Гелашвили Д. Б., Иудин Д. И., Розенберг Г. С., Якимов В. Н. Элементы фрактальной теории видовой структуры гидробиоценозов // Изв. СамНЦ РАН. 2006б. Т. 8. № 1. С. 70–79.
Гелашвили Д. Б., Иудин Д. И., Розенберг Г. С., Якимов В. Н., Солнцев Л. А. Основы мультифрактального анализа видовой структуры сообщества // Успехи соврем. биол. 2008в. Т. 128. № 1. С. 21–34.
Гелашвили Д. Б., Иудин Д. И., Розенберг Г. С., Якимов В. Н., Солнцев Л. А. Фракталы и мультифракталы в биоэкологии . Н. Новгород: Изд-во Нижегород. гос. ун-та, 2013а. 370 с.
Гелашвили Д. Б., Иудин Д. И., Розенберг Г. С., Якимов В. Н., Солнцев Л. А., Снегирёва М. С., Варичев А. Н. Фрактальные аспекты популяционной экологии // Вестн. Удмурт. ун-та. 2009а. Вып. 1. С. 15–22.
Гелашвили Д. Б., Иудин Д. И., Розенберг Г. С., Якимов В. Н., Шурганова Г. В. Степенной закон и принцип самоподобия в описании видовой структуры сообществ // Поволж. экол. журн. 2004. № 3. С. 227–245.
Гелашвили Д. Б., Иудин Д. И., Солнцев Л. А., Снегирёва М. С., Розенберг Г. С., Евланов И. А., Кириллова Н. Ю., Кириллов А. А. Мультифрактальный анализ видовой структуры сообществ гельминтов мелких млекопитающих Самарской Луки // Докл. Академии наук (ДАН). 2009б. Т. 427. № 5. С. 703–706.
Гелашвили Д. Б., Иудин Д. И., Якимов В. Н., Солнцев Л. А., Розенберг Г. С., Шурганова Г. В., Охапкин А. Г., Старцева Н. А., Пухнаревич Д. А., Снегирёва М. С. Мультифрактальный анализ видовой структуры пресноводных гидробиоценозов // Изв. РАН. Сер. биол. 2012. № 3. С. 327–335.
Гелашвили Д. Б., Розенберг Г. С., Иудин Д. И., Якимов В. Н., Солнцев Л. А. Фрактальные аспекты структурной устойчивости биотических сообществ // Биосфера. 2013б. Т. 5. № 2. С. 143–159.
Гелашвили Д. Б., Розенберг Г. С., Саксонов С. В., Иванова И. О., Вехник В. П. Видовая структура сообществ крупных млекопитающих Самарской Луки в связи с проблемой изменения климата // Изв. Самар. НЦ РАН. 2009в. Т. 11. № 1 (2). С. 28–41.
Гелашвили Д. Б., Саксонов С. В., Розенберг Г. С., Иудин Д. И., Снегирева М. С., Солнцев Л. А., Якимов В. Н. Флористический феномен Самарской Луки: фрактальная структура таксономического разнообразия // Самарская Лука: проблемы региональной и глобальной экологии: Бюл. 2011. Т. 20. № 2 (36). С. 80–104.
Гелашвили Д. Б., Якимов В. Н., Иудин Д. И., Розенберг Г. С., Солнцев С. А., Саксонов С. В., Снегирёва М. С. Фрактальные аспекты таксономического разнообразия // Журн. общ. биол. 2010б. Т. 71. № 2. С. 115–130.
Джиллер П. Структура сообществ и экологическая ниша . М.: Мир, 1988. 184 с.
Иванова А. В., Розенберг Г. С., Саксонов С. В. Опыт количественного анализа флористического разнообразия и флористической структуры Самарской Луки // Экология. 2006. № 5. С. 332–339.
Иудин Д. И. Методология принципа самоподобия в исследовании видовой структуры биотических сообществ : Дис. … д-ра биол. наук. Тольятти, 2006. 273 с.
Иудин Д. И., Гелашвили Д. Б. Применение мультифрактального анализа структуры биотических сообществ в экологическом мониторинге // Проблемы регионального экологического мониторинга: Материалы науч. конф. Н. Новгород: Изд-во ННГУ, 2002. С. 49–52.
Иудин Д. И., Гелашвили Д. Б., Розенберг Г. С. Мультифрактальный анализ видовой структуры биотических сообществ // Докл. Академии наук (ДАН). 2003. Т. 389. № 2. С. 279–282.
Иудин Д. И., Гелашвили Д. Б., Розенберг Г. С., Солнцев Л. А., Якимов В. Н. Биологические и экологические аспекты теории перколяции // Успехи совр. биол. 2010. Т. 130. № 5. С. 446–460.
Кафанов А. И., Суханов В. В. О зависимости между числом и объемом таксонов // Журн. общ. биол. 1981. Т. 42. № 3. С. 345–350.
Левич А. П. Структура экологических сообществ . М.: Изд-во МГУ, 1980. 180 c.
Лукичева А. Н., Сабуров Д. Н. Конкретная флора и флора ландшафта // Бот. журн. 1969. № 12. С. 1911–1920.
Майр Э. Принципы зоологической систематики . М.: Мир, 1971. 454 с.
Макаренко Н. Г. Фракталы, аттракторы, нейронные сети и все такое // Научная сессия МИФИ-2002. IV Всероссийская научно-техн. конф. «Нейроинформатика – 2002». Лекции по нейроинформатике. Ч. 2. М.: МИФИ, 2002. С. 121–169.
Мандельброт Б. Б. Фракталы и возрождение теории итераций // Пайген Х.-О., Рихтер П. Х. Красота фракталов. Образы комплексных динамических систем. М.: Мир, 1993. С. 131–140.
Мандельброт Б. Б. Фрактальная геометрия природы . М.; Ижевск: Ин-т компьют. иссл., 2002. 656 с.
Маргалеф Р. Облик биосферы . М.: Наука, 1992. 214 c.
Мельченко В. Е. Ландшафты Самарской Луки // Самарская Лука: Бюл. 1991. № 1. С. 45–62.
Миркин Б. М., Наумова Л. Г. Наука о растительности (история и современное состояние основных концепций) . Уфа: Гилем, 1998. 413 с.
Морозов А. Д. Введение в теорию фракталов . М.; Ижевск: Ин-т компьют. иссл., 2004. 160 с.
Одум Ю. Основы экологии . М.: Мир, 1975. 740 с.
Пайген Х.-О., Рихтер П. Х. Красота фракталов. Образы комплексных динамических систем . М.: Мир, 1993. 176 с. (Peitgen H.-O., Richter P. H. The Beauty of Fractals. Images of Complex Dynamical Systems. Heidelberg; N. Y.: Springer-Verlag, 1986. 199 р.).
Поздняков А. А. Проблема индивидности в таксономии // Журн. общ. биол. 2003. Т. 64. № 1. С. 55–64.
Поздняков А. А. Значение правила Виллиса для таксономии // Журн. общ. биол. 2005. Т. 66. № 4. С. 326–335.
Пузаченко Ю. Г. Приложение теории фракталов к изучению структуры ландшафта // Изв. РАН. Сер. геогр. 1997. № 2. С. 24–40.
Пузаченко Ю. Г., Пузаченко А. Ю. Семантические аспекты биоразнообразия // Журн. общ. биол. 1996. Т. 57. № 1. С. 5–43.
Розенберг Г. С. Статистические методы в фитоценологии на рубеже тысячелетий (к 50-летию выхода монографии П. Грейг-Смита) // Актуальные проблемы геоботаники: III Всерос. школа-конф: Лекции. Петрозаводск: КарНЦ РАН, 2007. С. 72–116.
Розенберг Г. С. Информационный индекс и разнообразие: Больцман, Котельников, Шеннон, Уивер… // Самарская Лука: проблемы региональной и глобальной экологии: Бюл. 2010. Т. 19. № 2. С. 4–25.
Розенберг Г. С. Введение в теоретическую экологию : В 2 т. Тольятти: Кассандра, 2013. Т. 1. 565 с.; Т. 2. 445 с.
Розенберг Г. С., Гелашвили Д. Б., Иудин И. Д. Фрактальная организация экосистем: нужно ли это нам // Экологические проблемы заповедных территорий России. Тольятти: ИЭВБ РАН, 2003а. С. 61–68.
Розенберг Г. С., Гелашвили Д. Б., Иудин Д. И. Фрактальная организация экосистем: cui prodest? // Эколого-географические проблемы природопользования нефтегазовых регионов: Теория, методы, практика: Материалы II Междунар. научно-практ. конф. Нижневартовск: НГПИ, 2003б. С. 342–347.
Розенберг Г. С., Гелашвили Д. Б., Иудин Д. И. Фракталы – новый язык теоретической экологии // Сб. тр. Первого междунар. экологического конгресса (третьей междунар. научно-техн. конф.) «Экология и безопасность жизнедеятельности промышленно-транспортных комплексов» ELPIT 2007 (20–23 сентября 2007 г., Тольятти, Россия). Т. 1. Тольятти: ТолГУ, 2007. С. 4–9.
Розенберг Г. С., Мозговой Д. П., Гелашвили Д. Б. Экология. Элементы теоретических конструкций современной экологии . Самара: СНЦ РАН, 1999. 396 с.
Рощевский Ю. К. Самарская Лука // Заповедники СССР. Национальные парки и заказники. М.: ABF, 1996. С. 34–43.
Рябко Б. Я., Кудрин Б. И., Завалишин Н. Н., Кудрин А. И. Модель формирования статистической структуры биоценоза // Изв. АН СССР. Сер. биол. 1978. Вып. 1. С. 121–127.
Саксонов С. В. Основы крупномасштабного флористического районирования Самарской Луки (Восток Центральной части Приволжской возвышенности) // Самарская Лука: Бюл. 1996. № 7. С. 70–98.
Саксонов С. В. Самаролукский флористический феномен . М.: Наука, 2006. 263 с.
Уилкокс Б. Островная экология и охрана природы // Биология охраны природы. М.: Мир, 1983. С. 117–142.
Федер Е. Фракталы . М.: Мир, 1991. 254 с. (Feder J. Fractals. N. Y.: Plenum Pub. Corp., 1988. 283 р.).
Федоров В. Д. Относительное обилие симпатрических видов и модель экспоненциально разломанного стержня // Человек и биосфера. М.: Изд-во МГУ, 1978. Вып. 2. С. 17–41.
Филиппов А. Э. Дискретное видообразование и закон Виллиса // Журн. общ. биол. 1984. Т. 45. № 3. С. 410–418.
Чертопруд М. В., Азовский А. И. Размещение макробентоса беломорской литорали в различных масштабах пространства // Журн. общ. биол. 2000. Т. 61. № 1. С. 47–63.
Численко Л. Л. О структуре таксонов и таксономическом разнообразии // Журн. общ. биол. 1977. Т. 38. № 3. С. 348–358.
Шаталкин А. И. Иерархии в систематике. Теоретико-множественная модель // Журн. общ. биол. 1995. Т. 56. № 3. С. 277–290.
Шитиков В. К., Розенберг Г. С., Зинченко Т. Д. Количественная гидроэкология: методы, критерии, решения : В 2 кн. М.: Наука, 2005. Кн. 1. 281 с.; Кн. 2. 337 с.
Шредер М. Фракталы, хаос, степенные законы. Миниатюры из бесконечного рая . М.; Ижевск: Ин-т компьют. иссл., 2001. 528 c.
Якимов В. Н. Фрактальность видовой и пространственной структуры биологических сообществ: разработка концепции и верификация : Дис. ... канд. биол. наук. Н. Новгород, 2007. 125 с.
Якимов В. Н., Гелашвили Д. Б., Иудин Д. И., Розенберг Г. С., Маркелов И. Н. Универсальность скейлинга разнообразия в нейтральных и нишевых моделях экологических сообществ // Междунар. науч.-исслед. журн. 2016а. № 12 (54). Ч. 1. С. 40–45.
Якимов В. Н., Гелашвили Д. Б., Розенберг Г. С., Безель В. С. Скейлинг филогенетического разнообразия в сообществах мелких млекопитающих (на примере Нижегородского Поволжья) // Экология. 2017. № 3. С. 210–215.
Якимов В. Н., Гелашвили Д. Б., Розенберг Г. С., Кривоногов Д. М. Современные методы количественного анализа филогенетического разнообразия экологических сообщества // Аспекты биоразнообразия: Сб. трудов Зоологического музея МГУ им. М. В. Ломоносова. М.: Тов-во науч. изд. КМК, 2016б. Т. 54 (1). Ч. 1. С. 72–98.
Якимов В. Н., Солнцев Л. А., Иудин Д. И., Розенберг Г. С., Гелашвили Д. Б. Нарушения канонической формы мультифрактального спектра пространственной структуры сообщества: причины возникновения и пути решени // Изв. Самар. НЦ РАН. 2014а. Т. 16. № 1. С. 19–26.
Якимов В. Н., Солнцев Л. А., Розенберг Г. С., Иудин Д. И., Гелашвили Д. Б. Масштабная инвариантность биосистем: от эмбриона до сообщества // Онтогенез. 2014б. Т. 45. № 3. С. 207–216.
Якимов В. Н., Солнцев Л. А., Розенберг Г. С., Иудин Д. И., Широков A. И., Локтева О. А., Гелашвили Д. Б. Локальный мультифрактальный анализ пространственной структуры луговых сообществ в малых масштабах // Докл. Академии наук (ДАН). 2014в. Т. 458. С. 613–617.
A maverick’s apprenticeship. The Wolf Prize for Physics / Ed. by D. Thouless. Singapore: World Scientific, 2004.
Azovsky A. I. Concept of scale in marine ecology: linking the words or the worlds? // Web Ecol. 2000. № 1. Р. 28–34. URL: http://www.oikos.ekol.lu.se/we/we.html (дата обращения: 25.10.2007).
Azovsky A. I., Chertoprood M. V., Kucheruk N. V., Rybnikov P. V., Sapozhnikov F. V. Fractal properties of spatial distribution of intertidal benthic communities // Marine Biol. 2000. Vol. 136. No 3. P. 581–590.
Bak P., Tang C., Weisenfeld K. Self-organized criticality // Phys. Rev. 1988. A 38. P. 364–374.
Bossuyt B., Hermy M. Species turnover at small scales in dune slack plant communities // Basic and Applied Ecol. 2004. Vol. 5. P. 321–329.
Brown J. H., Gupta V. K., Li B. L., Milne B. T., Restrepo C., West G. B. The fractal nature of nature: power laws, ecological complexity and biodiversity // Philos. Trans. R. Soc. Lond. B. Biol. Sci. 2002. Vol. 357. No 1421. P. 619–626.
Buck R. C., Hull D. L. The logical structure of the Linnean hierarchy // Syst. Zool. 1966. Vol. 15. P. 97–111.
Burlando B. The fractal dimension of taxonomic systems // J. Theor. Biol. 1990. Vol. 146. P. 99–114.
Burlando B. The fractal geometry of evolution. // J. Theor. Biol. 1993. Vol. 163. P. 161–172.
Dicke M., Burrough P. A. Using fractal dimensions for characterizing tortuosity of animal trails // Physiol. Entomol. 1988. Vol. 13. P. 393–398.
Gelashvili D. B., Iudin D. I., Rozenberg G. S., Solntsev L. A., Ivanova I. O. Species structure of communities: explanation and forecast under "global warming" scenario (fractal theory approach) // Climate Change and Possible Implications for the Volga Basin Ecosystem. The Volga River Basin in 50 Years: Perspectives and Forecast: Materials of the Conference. Togliatti: British Council, 2007. P. 11–13.
Gleason H. A. On the relation between species and area // Ecology. 1922. Vol. 3. P. 158–162.
Green D. M. Chaos, fractals and nonlinear dynamics in evolution and phylogeny // Trends in Ecology and Evolution. 1991. Vol. 6. P. 333–337.
Green J. L., Harte J., Ostling A. Species richness, endemism and abundance patterns: tests of two fractal models in a serpentine grassland // Ecol. Letters. 2003. Vol. 6. P. 919–928.
Harte J., Kinzig A. P., Green J. L. Self-similarity in the distribution and abundance of species // Science. 1999. Vol. 284. P. 334–336.
In his own words: BBM Interview by Anthony Barcellos // Mathematical People / Ed. by D. J. Albers & G. L. Alexanderson. Boston: Birkhäuser, 1985. P. 205–225.
Iudin D. I., Gelashvili D. B. Multifractality in ecological monitoring // Nucl. Instr. Meth. Phys. Res. 2003. Vol. 502. P. 799–801.
Iudin D. I., Gelashvili D. B., Rozenberg G. S., Solntcev L. A., Yakimov V. N. Bases of the multifractal analysis of species structure of community // Types of Strategy and Not Only… (Materials of the Fourth Russian-Polish School of Young Ecologists; Togliatti, September, 6–12th, 2010) / Editor-in-chief G. S. Rozenberg. Togliatti: Kassandra, 2010. P. 17–19.
Laurie H., Perrier E. A multi-fractal model for the species–area relationship. 2006. 18 p. URL: www.mth.uct.ac.za/~henri/multfrac6par.pdf (дата обращения: 12.12.2009).
Li B.-L. Fractal geometry applications in description and analysis of patch patterns and patch dynamics // Ecol. Model. 2000. Vol. 132. P. 33–50.
MacArthur R. H. On the relative abundance of species // Amer. Nat. 1960. Vol. 94. P. 25–36.
MacArthur R. H., Wilson E. O. The Theory of Island Biogeography. Princeton (NJ): Princ. Univ. Press, 1967. 203 p. .
Mandelbrot B. B. How long is the coast of Britain? Statistical self-similarity and fractional dimension // Science. 1967. Vol. 156. No 3775. P. 636–638.
Mandelbrot B. B. Fractals: Form, Chance and Dimension. San Francisco (CA): W. H. Freeman and Co., 1977. 265 p.
Morse D. R., Lawton J. H., Dodson M. M., Williamson M. H. Fractal dimension of vegetation and the distribution of arthropod body lengths // Nature. 1985. Vol. 314. No 6013. P. 731–733.
Motomura I. A statistical treatment of associations // Jap. J. Zool. 1932. Vol. 44. P. 379–383.
Pachepsky Yа. A., Gimenez D., Crawford J. W., Rawls W. J. Conventional and fractal geometry in soil science // Fractals in Soil Science / Ed. by Ya. Pachepsky, J. Crawford, W. Rawls. Amsterdam; N. Y.: Elsevier, 2000a. P. 7–18.
Pachepsky Yа. A., Gimenez D., Crawford J. W., Rawls W. J. Bibliography on applications of fractals in soil science // Fractals in Soil Science / Ed. by Ya. Pachepsky, J. Crawford, W. Rawls. Amsterdam; N. Y.: Elsevier, 2000b. P. 273–295.
Pachepsky Yа. A., Ritchie J. C. Seasonal changes in fractal landscape surface roughness estimated from airborne laser altimetry data // Int. J. Remote Sensing. 1998. Vol. 19. P. 2509–2516.
Pachepsky Yа. A., Timlin D. Water transport in soils as in fractal media // J. Hydrology. 1998. Vol. 204. No 1. P. 98–107.
Pounds J. A., Puschendorf R. Clouded futures // Nature. 2004. Vol. 427. P. 107–109.
Preston F. W. The canonical distribution of commonness and rarity: Part I // Ecology. 1962. Vol. 43. No 2. P. 185–215.
Rosenzweig M. L. On continental steady states of species diversity // M. L. Cody, J. M. Diamond (Eds.). Ecology and Evolution of Communities. Cambridge (Mass.): Harvard Univ. Press, 1975. P. 121–140.
Scheuring I. The fractal nature of vegetation and the species-area relation // Theor. Populat. Biol. 1991. Vol. 39. P. 170–177.
Scheuring I., Riedi R. H. Application of multifractals to the analysis of vegetation patterns // J. Veg. Sci. 1994. Vol. 5. P. 489–496.
Seuront L. Fractals and Multifractals in Ecology and Aquatic Science. Boca Raton (FL): CRC Press, 2010. 344 p.
Seuront L., Schmitt F., Lagadeuc Y., Schertzer D., Lovejoy S., Frontier S. Multifractal analysis of phytoplankton biomass and temperature in the ocean // Geophys. Res. Lett. 1996. Vol. 23. P. 3591–3594.
Sugihara G., May R. M. Applications of fractals in ecology // Trends in Ecology and Evolution. 1990. Vol. 5. P. 79–86.
Turchin P. Fractal analysis of animal movement: a critique // Ecology. 1996. Vol. 77. P. 2086–2090.
Wagensberg J. In memoriam. Benoit Mandelbrot y la fractalidad del mundo // El País. 19.10.2010. 44 p.
Willis J. C. The Course of Evolution by Differentiation or Divergent Mutation Rather than by Selection. London: Cambridge Univ. Press, 1940. 207 p.
With K. A., Cadaret S. J., Davis C. Movement responses to patch structure in experimental fractal landscapes // Ecology. 1999. Vol. 80. P. 1340–1353.
Yakimov B. N., Gelashvili D. B., Solntsev L. A., Iudin D. I., Rozenberg G. S. Nonconcavity of mass exponents’ spectrum in multifractal analysis of community spatial structure: The problem and possible solutions // Ecological Complexity. 2014. Vol. 20. P. 11–22.
Zeide B. Fractal geometry in forestry applications // For. Ecol. Manage. 1991. Vol. 46. P. 179–188.
Zhang Y., Ma K., Anand M., Fu B. Do generalized scaling laws exist for species abundance distribution in mountains? // Oikos. 2006. Vol. 115. P. 81–88.
Благодарности
Я выражаю глубокую благодарность своим коллегам – профессору, д. б. н. Д. Б. Гелашвили, профессору, д. ф.-м. н. и д. б. н. Д. И. Иудину и доценту, д. б. н. В. Н. Якимову (Национальный исследовательский Нижегородский государственный университет им. Н. И. Лобачевского) – за многолетнее сотрудничество по внедрению в отечественное «экологическое сознание» методов фрактальной геометрии. Работа выполнена при финансовой поддержке Программы фундаментальных научных исследований государственных академий наук на 2013–2020 годы по теме «Экологические закономерности структурно-функциональной организации, ресурсного потенциала и устойчивого функционирования экосистем Волжского бассейна», № AAAA-A17-117112040039-7.





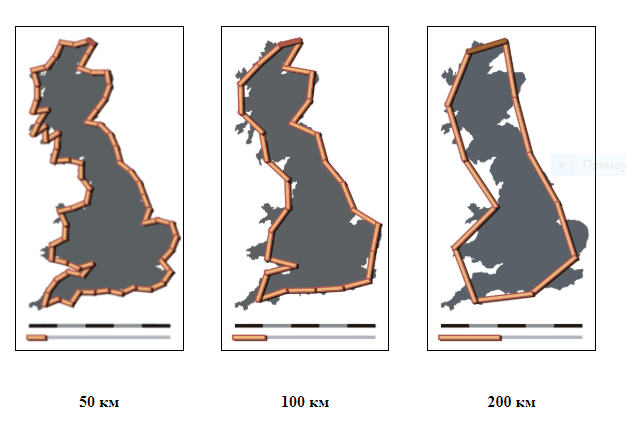







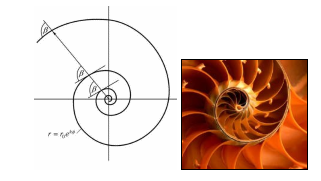
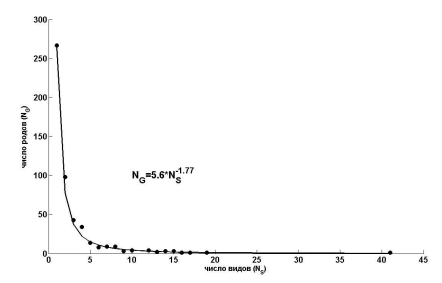
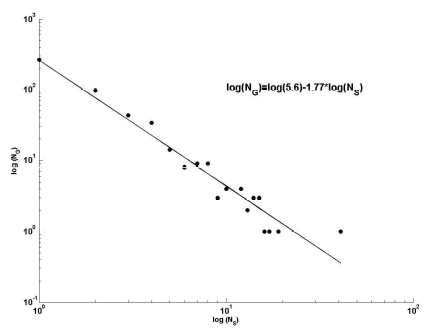
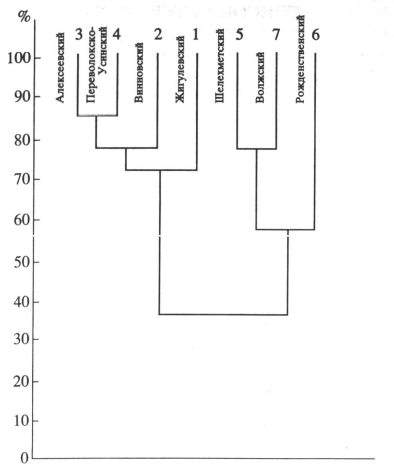
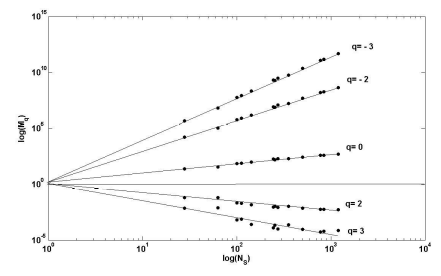
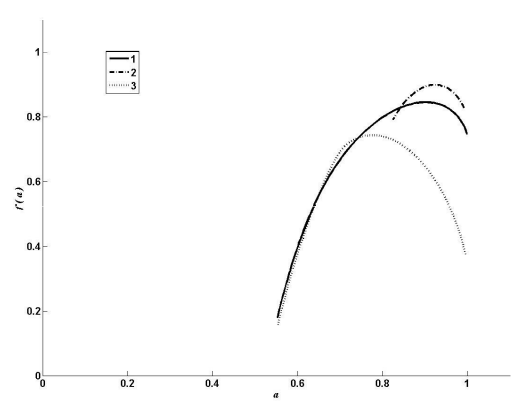

 © 2011 - 2026
© 2011 - 2026