Введение
При анализе экологических данных часто ограничиваются вычислением точечных оценок изучаемых показателей по имеющимся выборкам (например, арифметических средних). Как правило, этого недостаточно – следует убедиться в том, что найденная величина, например средней популяционной плотности животных, является точной и несмещенной, а также получить ее надежные доверительные интервалы. Или если сравнивается видовой состав для двух или нескольких местообитаний, то необходимо оценить вероятность того, что найденное сходство биотопов по Съеренсену статистически значимо отличается от случайного распределения. Только так мы можем обосновать то, что изменчивость показателей обилия организмов имеет экологически закономерный характер. В противном случае мы вынуждены принять нуль-предположение, что видовой состав на всей площади изучаемого региона сформировался как случайные выборки из некого гипотетического резервуара видов бесконечной емкости (или по-английски – heat bath) в результате каких-то непредсказуемых стохастических событий. И тут есть две проблемы. Во-первых, статистические свойства параметров могут быть изучены только при наличии повторностей наблюдений. Однако в экологии можно выполнить срез данных только в определенном месте и в определенный момент времени, а если отбирать вторую, третью пробы и т. д., то это будут уже данные из другого места или же взятые в другой момент времени. Поэтому возникает вопрос: как, имея лишь одну единственную повторность, оценить значение необходимого нам показателя и получить меру точности этой оценки? Во-вторых, поскольку точный вид распределения обрабатываемых данных, как правило, неизвестен, используют приближенные методы аппроксимации предполагаемых свойств исследуемой статистики, причем как влияет степень этой приближенности на окончательные выводы, остается целиком на совести исследователя. В частности, классическая теория проверки статистических гипотез использует то или иное стандартное предельное выборочное распределение (Гаусса, Стьюдента, Фишера и др.), оценивая их параметры по выборочным данным. В этой связи обработка экологических наблюдений параметрическими методами, описанными во всех учебниках по биометрии, основывается на целом ряде априорных предположений, таких как независимость измерений и их ошибок, однородность дисперсий, нормальность распределения и проч. Если они верны, то тесты обладают несомненной надежностью и прекрасной теоретической проработанностью. В то же время возможные отклонения от этих предположений, характерные для экологических данных, могут серьезно повлиять на обоснованность конечных выводов. Современной альтернативой параметрическим методам является моделирование эмпирического распределения данных с использованием методов генерации повторных выборок (или численного ресамплинга – resampling), которые бурно развиваются два последних десятилетия. Методы ресамплинга объединяют три разных подхода, отличающихся по алгоритму, но близких по сути: рандомизацию, или перестановочный тест (permutation), бутстреп (bootstrap) и метод «складного ножа» (jackknife). К сожалению, русскоязычному читателю трудно встретить публикации, посвященные этой динамично развивающейся идеологии, поэтому в нашем сообщении мы приведем краткое изложение ее сути и проиллюстрируем возможности применения перечисленных методов на конкретных примерах гидробиологического плана. Исходными данными для расчетов явились экспедиционные материалы лабораторий Института экологии Волжского бассейна РАН (рук. Т. Д. Зинченко, д.б.н. и О. А. Розенцвет). Большинство вычислений (рис. 1‒7) выполнены с использованием простой и удобной программы Resampling Procedures 1.3, разработанной и свободно распространяемой Д. Хауэллом, профессором университета в Вермонте, автором книги «Статистические методы в психологии», выдержавшей семь изданий; на его сайте приведены также детальные рекомендации по использованию методов (Howell, 2007).
Аналитический обзор
1. Обзор методов ресамплинга
Идеи численного ресамплинга не являются принципиально новыми в статистике и относятся по крайней мере к 1935 г., но практическое применение этих методик было связано с вынужденым ожиданием, пока не появятся достаточно быстрые компьютеры. Идея метода «складного ножа» (или jackknife) заключается в том, чтобы последовательно и многократно исключать из имеющейся выборки, насчитывающей n элементов, по одному ее члену и обрабатывать вариационный ряд из оставшихся (n – 1) элементов (Tukey, 1958). Среднее значение или медиана будет при этом «блуждать» и тогда можно проанализировать информацию о каждом акте смещения, построить распределение выборочной оценки искомого параметра и уточнить его свойства. Ф. Мостеллер и Дж. Тьюки (1982) считали этот алгоритм «универсальной методикой подобно бойскаутскому ножу, годящемуся на все случаи жизни» (с. 143).
Бутстреп-процедура (или bootstrap) была предложена (Efron, 1979) как некоторое обобщение алгоритма «складного ножа», чтобы не уменьшать каждый раз число элементов по сравнению с исходной совокупностью. По одной из версий слово «bootstrap» означает кожаную полоску в виде петли, прикрепляемую к заднику походного ботинка для облегчения его натягивания на ногу. Благодаря этому термину появилась английская поговорка 1930-х г.: «Lift oneself by the bootstrap», которую можно трактовать как «Пробить себе дорогу благодаря собственным усилиям» (или подобно барону Мюнхгаузену вытянуть себя из болота за шнурки от ботинок).
Основная идея бутстрепа по Б. Эфрону (1988) состоит в том, чтобы методом статистических испытаний Монте-Карло многократно извлекать повторные выборки из эмпирического распределения. А именно: берется конечная совокупность из n членов исходной выборки x1, x2, …, xn-1, xn , откуда на каждом шаге из n последовательных итераций с помощью датчика случайных чисел, равномерно распределенных на интервале [1, n], «вытягивается» произвольный элемент xk, который снова «возвращается» в исходную выборку (т. е. может быть извлечен повторно). Например, при n = 8 одна из таких комбинаций имеет вид x4, x2, x8, x2, x1, x2, x4, x5, т. е. отдельные элементы могут повторяться. Этим способом можно сформировать любое, сколь угодно большое число бутстреп-выборок. Как и в случае «складного ножа», в результате легкой модификации частотного распределения реализаций исходных данных можно ожидать, что каждая следующая генерируемая псевдовыборка будет возвращать значение параметра, немного отличающееся от вычисленного для первоначальной совокупности. Образующийся разброс значений показателя дает возможность построения доверительных интервалов и других полезных выборочных параметров анализируемой величины (Manly, 2007).
Одновременно с внедрением методов планирования эксперимента начали бурно развиваться алгоритмы рандомизации, которые заключаются в многократном случайном перемешивании строк или столбцов таблицы наблюдений относительно уровней воздействия изучаемых факторов. При каждой итерации перестановочного теста на основе сгенерированной псевдовыборки рассчитываются имитируемые значения tran анализируемого показателя или статистики, которые сравниваются с аналогичной величиной tobs, найденной по эмпирическим данным. В ходе перестановок не меняется ни состав исходной таблицы, ни численность групп с разными уровнями воздействия, а только происходит беспорядочный обмен элементами данных между этими группами.
Существуют мнения (Manly, 2007), что рандомизация вообще является частным случаем испытаний Монте-Карло (см. первые работы Бюффона в1777 г.). Однако несмотря на сходство этих методов в основных алгоритмах и ограничениях, между ними есть весьма существенные концептуальные различия (например, для методов Монте-Карло типичны исследования, когда данные наблюдений вообще не используются, чтобы смоделировать вероятностный процесс).
Процедуры ресамплинга не требуют никакой априорной информации о законе распределения изучаемой случайной величины и в этом смысле могут рассматриваться как непараметрические. Они выполняют обработку различных фрагментов исходного массива эмпирических данных, как бы поворачивая их «разными гранями» и сопоставляя полученные таким образом результаты. Вопрос о полной корректности такого приема остается открытым, но если признать его законным, то асимптотические достоинства ресамплинга по сравнению с классическими параметрическими тестами становятся очевидными. Значения параметров, построенных по размноженным подвыборкам, строго говоря, не являются независимыми, однако при увеличении n с ресамплированными значениями статистик можно обращаться как с независимыми случайными величинами.
2. Уточнение выборочных параметров и построение доверительных интервалов
Фундаментальной проблемой статистики является получение наиболее корректной оценки параметров выборочного распределения. Пусть дана выборка x1, x2, …, xn и предполагается, что это – набор независимых и одинаково распределенных реализаций случайной величины, извлеченных из генеральной совокупности X. Задача заключается в изучении свойств некоторой статистики fn (x1, x2, …, xn), которую мы трактуем как выборочную оценку произвольного параметра распределения X. Обычно мы имеем некоторый сдвиг b = E(q ‒ ) вычисленного значения параметра относительно его истинной величины q, который вызывается многими причинами. Во-первых, выборочные значения имеют погрешность измерений, во-вторых, нет особенных гарантий, что выборка состоит из независимых и случайных значений, и, наконец, при оценке параметра мы обычно задаемся какими-то предположениями о законе распределения Х.
Например, в случае нормального распределения Х оценкой меры положения случайной величины является арифметическое среднее, а несмещенной оценкой дисперсии s2 − квадрат стандартного отклонения s2. Однако так ли это на самом деле и справедливы ли наши исходные допущения? Один из способов проверить вычисления заключается в том, чтобы извлекать из нашей генеральной совокупности все новые и новые повторные выборки, пересчитывать на этой основе оценки параметров и анализировать дрейф . Бутстреп предоставляет более экономный способ, позволяющий обойтись без дополнительных измерений, а построить, например, доверительные интервалы анализируемой статистики на основе разброса значений анализируемого показателя, полученного в процессе имитации.
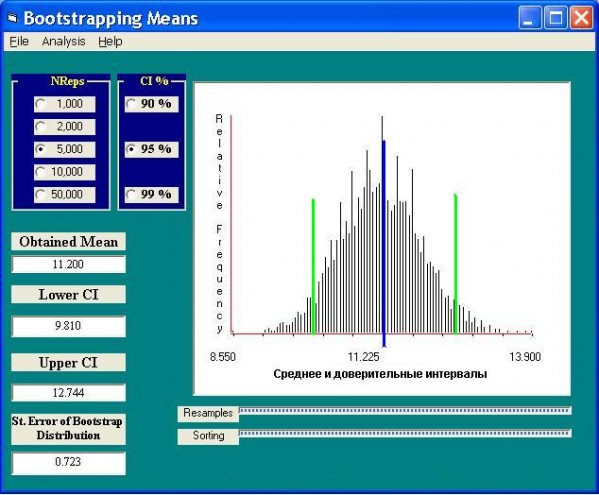
Предположим, что требуется оценить среднее число видов макрозообентоса в одной пробе из р. Байтуган по 40 выполненным измерениям. Выполним 5000 итераций бутстрепа и для каждой сгенерированной псевдовыборки вычислим частные значения среднего и стандартного отклонения. На основе этих имитированных данных по восстановленной гистограмме частотного распределения (рис. 1) легко вычислить улучшенные бутстрепом общие значения среднего и стандартного отклонения, а также найти граничные значения точечного богатства видов при 95%-й доверительной вероятности, не используя при этом предположений о нормальном характере распределения исходных данных. Если для этой выборки рассчитать средние и их доверительные интервалы обычным способом по известным формулам, то полученные значения почти совпадают с бутстрепированными, поскольку анализируемый ряд достаточно гладок и симметричен.
Проанализируем, однако, значения другого ряда – численности Chironomus salinarius в 43 пробах, где этот вид был обнаружен (в скобках – частоты значений):
5 (2); 8; 10 (3); 19; 20 (3); 30; 40; 42; 50 (6); 65 (2); 80 (3); 100 (2); 133; 200; 250; 300;
430; 440; 480; 800; 880; 2400; 3020; 3360; 5200; 6200; 7000; 9000; 19000.
В этом случае (рис. 2) коррекция параметров, выполненная бутстрепом, по сравнению со значениями, полученными по обычным формулам, дает весьма существенный эффект: среднее оказывается около 2000 экз. /м2 вместо 1400, а верхняя граница доверительного интервала становится 3700 экз. /м2 вместо 2500.
Рис. 1. Моделирование параметров распределения числа видов в пробах бентоса с использованием модуля Resampling Procedures 1.3 (Howell, 2001). Здесь и далее на рис. 2‒7: NReps – число генерируемых псевдовыборок; CI – доверительная вероятность; Obtained Mean – среднее, скорректированное бутстреп-методом (линия синего цвета); Lower и Upper CI – соответственно нижняя и верхняя границы доверительного интервала (зеленые линии); St. Error of Bootstrap Distribution – стандартное бутстрепированное отклонение.
Fig. 1. The simulation of the count species distribution parameters at the bentos samples by the bootstrep-method using the module Resampling Procedures 1.3 (Howell, 2001)
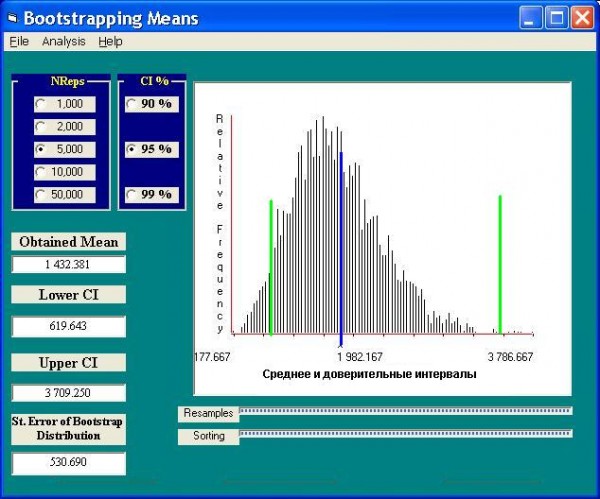
Рис. 2. Моделирование параметров распределения оценок численности Chironomus salinarius бутстреп-методом
Fig. 2. The simulation of the estimations of Chironomus salinarius abundance distribution parameters by the bootstrep-method
С помощью бутстрепа можно делать то, что не всегда под силу обычным параметрическим методам. Например, для асимметричных выборок часто предлагают использовать медиану в качестве оценки меры положения случайной величины вместо математического ожидания. Если распределение данных близко к нормальному, то стандартную ошибку медианы можно приближенно оценить по формуле 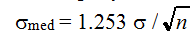
Бутстреп-метод позволяет сгенерировать из исходной выборки 5000 псевдомедиан и можно легко рассчитать и стандартную ошибку медианы, и ее доверительные интервалы. Например, для той же численности Chironomus salinarius значение медианы равно 80, что, кстати, значительно меньше среднего арифметического, а нижняя граница доверительного интервала вообще «вылетает» в отрицательную область (рис. 3). Еще более парадоксальные результаты можно получить, если добавить к представленной выборке пять сотен значащих нулей, т. е. те пробы, в которых Chironomus salinarius вообще не встретился. Так что с огорчением следует признать, что за 200 лет гидробиологии не удалось договориться о том, что считать за параметр центра выборочного распределения популяционной плотности.
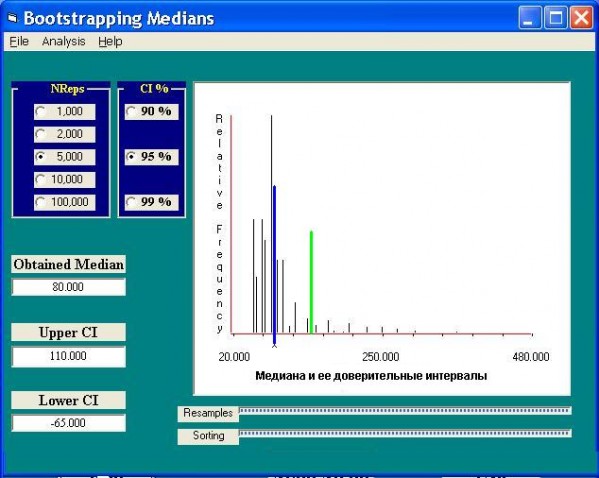
Рис. 3. Расчет доверительных интервалов медианы численностей Chironomus salinarius бутстреп-методом
Fig. 3. The calculation of the median abundance Chironomus salinarius confidential intervals by the bootstrep-method
Важное место в экологических исследованиях занимают индексы, основанные на аддитивных вкладах совокупности видов, образующих сообщество (индекс видового разнообразия Шеннона, индекс Симпсона и т. д.). Естественно, что сравнение экологических объектов с использованием таких индексов должно проводиться с учетом доверительных интервалов: если, например, рассчитанные 95%-е доверительные области двух индексов Шеннона пересекаются, то нет оснований отклонять нулевую гипотезу, а биоразнообразие сопоставляемых сообществ не отличается между собой.
Предположим, что необходимо рассчитать W-статистику Кларка, оценивающую площадь между двумя кумулятивными кривыми обилия бентосных организмов:
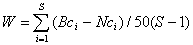 ,
,
где Bci и Nci – накопленные относительные значения биомассы и численности (%) для i-го по рангу вида; S – число видов. Если W > 0, то кумулятивная кривая биомассы располагается выше кривой численности, что, согласно АВС-методу Р.Уорвика (Abundance/Biomass Comparisons – см. публикации Warwick and Clarke, 1986-1992 гг.), является признаком устойчиво развивающегося сообщества. Отрицательное значение W-статистики свидетельствует о доминировании в сообществе r-стратегов и вероятности стрессового воздействия. Ниже представлен фрагмент списка видов макрозообентоса для расчета величины W по результатам гидробиологической съемки на р. Камышла:
Виды Bc Nc Bc - Nc
1 Limnodrilus sp. 98.79 74.02 24.77
2 Tubifex tubifex 93.29 82.41 10.88
3 Micropsectra gr.praecox 97.64 93.44 4.20
4 Limnodrilus hoffmeisteri 98.49 95.13 3.35
…
33 Tipula luna 91.02 98.80 -7.77
34 Dicranota sp 88.04 97.33 -9.29
35 Pseudodiamesa branickii 76.76 90.10 -13.34
18.48 W = 0.011
Оценку стандартных ошибок и 95%-х доверительных интервалов W можно провести бутстреп-методом. Для этого многократно (например, 500 раз) случайным образом с возвращением формируются псевдовыборки из S видов, т. е. на каждой итерации некоторые виды могут отсутствовать, а другие – повторяться два раза или более. Для каждой случайной комбинации видов рассчитывается значение тестируемого показателя и восстанавливается неизвестное статистическое распределение значений W для анализируемого водотока. Будем использовать для расчетов модули forams и bootstrap для статистической среды R и в результате получим стандартную ошибку sW = 0.0202 и доверительные границы показателя от ‒0.029 до 0.05. Для р. Сосновка значение W = 0.07±0.039 (доверительные границы от ‒0.004 до 0.148) и нет оснований полагать, что эти водотоки отличаются по уровню доминирования видов с r-стратегией, поскольку их 95%-е доверительные интервалы пересекаются. Та же методика может быть использована, например, при сравнении видового разнообразия объектов по индексу Шеннона.
3. Проверка статистических гипотез с использованием рандомизации
Основной задачей анализа экологических данных является поиск ответов на ключевые вопросы: отличаются ли между собой две выборки или несколько выборок, является ли статистически значимым группировочный фактор, имеется ли корреляционная связь между изучаемыми переменными и т. д. Эти задачи сводятся к оценке р-значения, «которое является условной вероятностью получить наблюдаемое значение tobs статистики некоего критерия T (и все остальные еще менее вероятные значения этой статистики) при условии, что верна нулевая гипотеза H0» (Хромов-Борисов, 2011). Например, если необходимо оценить, насколько значимо различие средних в двух полученных выборках, рекомендуется вычислить z-критерий или t-статистику Стьюдента и определить соответствующее им значение вероятности р. Если ее величина меньше, предположим, одной тысячной, то нет веских оснований предполагать, что выборки взяты из одной генеральной совокупности. В случае, если величина вероятности р больше 0.05, то нельзя утверждать без серьезного риска ошибиться, что обе выборки отличаются между собой.
Параметрические тесты, использующие популярные статистические критерии (t, z, F и проч.), оценивают не то, насколько близки сами данные в сопоставляемых вариационных рядах, а равны ли их отдельные выборочные параметры. Например, если нужно сравнить две группы наблюдений при разных уровнях воздействия изучаемого фактора, то оценка отличий выборок фактически сводится к сравнению их средних (что не вполне одно и то же): т. е. формулируется гипотеза H0: m1 = m2 и с помощью t-критерия делается частное заключение о равенстве центров распределения обеих групп. При использовании общепринятых непараметрических тестов (например, на основе критерия Манна-Уитни-Вилкоксона) анализ становится еще менее определенным и оперирует уже не со средними, а с такими трудно интерпретируемыми и не вполне точными понятиями, как «сдвиг местоположения». Важно отметить, что после того, как рассчитан выборочный критерий tobs, исходная совокупность отстраняется от дальнейшей обработки и в оценке самого р-значения никакого участия не принимает.
Для того чтобы корректно применять параметрические критерии, необходимо задаться целым рядом предположений: например, что обе сравниваемые совокупности распределены по нормальному закону и у них одинаковая дисперсия. Только в этих условиях t-статистика имеет характерное стандартное распределение в условиях справедливости нулевой гипотезы, которое вырождается (т. е. уходит в область низких вероятностей), если эмпирические данные не соответствуют H0. Приходится либо принимать на веру нормальность и гомоскедастичность выборок, либо проверять эти утверждения с использованием других статистических критериев.
Рандомизация основана на двух концепциях: а) нуль-модели, которая представляет собой образ (имитацию структуры) наблюдаемых данных, сформированный из предположения, что H0 верна, и б) процесса Монте-Карло, позволяющего восстановить плотность распределения оценок вероятности анализируемого критерия. Алгоритм выполнения рандомизационного теста (другой термин – «перестановка» или permutation) для схемы сравнения двух независимых выборок выглядит следующим образом:
- Выбираем произвольную метрику Т, позволяющую оценить статистическую значимость различий двух групп данных (для определенности будем использовать традиционную статистику Стьюдента
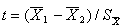 .
. - Вычисляем значение тестируемой статистической величины для исходных (эмпирических) данных, которую обозначим как tobs.
- Повторяем N раз следующие действия, где N – число, большее, чем 1000:
- объединяем данные из обеих выборок и перемешиваем их случайным образом;
- первые n1 наблюдений назначаем в первую группу, а остальные n2 наблюдения отправляем во вторую;
- вычисляем тестовую статистику tran для рандомизированных данных;
- если tran > tobs ,то увеличиваем на 1 счетчик S (т. е. используем односторонний тест).
- Разделив значение S на N, получим относительную частоту, с которой метрика tran на рандомизированных данных превышает значение tobs на данных, которые мы получили в эксперименте. Иными словами, вычисляем оценку вероятности р того, что случайная величина Т примет значение, большее, чем tobs. По традиции, если р > 0.05, то принимается нулевая гипотеза H0 об отсутствии значимых отличий исходных выборок от их нуль-модели по индексу Т, а если р меньше задаваемого уровня значимости, то H0 отклоняется в пользу альтернативы.
Очевидно, что в ходе перестановок не меняется ни состав исходной таблицы, ни численность групп с разными уровнями воздействия, а только происходит беспорядочный обмен элементами данных между этими группами. Интересно, что вместо традиционного t-критерия можно использовать и иные меры, такие как разность между средними или даже среднее для первой выборки. Подчеркнем, что здесь не имеется в виду проверка гипотезы о различии между внутригрупповыми средними, а значение t используется просто как один из подходящих индексов, измеряющих «неодинаковость» выборок. Точно так же можно оценить различие дисперсий или коэффициентов вариаций, любых метрик сходства выборок и проч. Инвариантность теста относительно критерия T позволяет сделать приведенное выше определение более лаконичным: «P-значение (или достигнутый уровень значимости) есть условная вероятность получить наблюдаемую совокупность данных при условии, что верна нулевая гипотеза H0 ».
Предположим, что необходимо выяснить, отличается ли точечное видовое разнообразие зообентоса для верхнего (51 проба) и нижнего (44 пробы) участков р. Сок. Сформируем две выборки из значений индекса Шеннона, рассчитанных для каждой пробы зообентоса, и найдем значение нормированной разности средних (т. е. t-статистики) между этими группами, равное 1.25. Сформируем еще 5000 пар псевдовыборок для таких групп, каждый раз случайно перемешивая исходные 95 индексов Шеннона, и получим возможное частотное распределение t-статистики при отсутствии различий между группами. Наше испытуемое значение расположено где-то внутри этого распределения (рис. 4), в частности, 1089 нуль-модельных комбинаций из 5000 превышают по абсолютной величине эмпирическую t-статистику. Следовательно, Р-значение равно 0.2178, отклонять нулевую гипотезу нельзя и мы принимаем утверждение, что видовое разнообразие зообентоса в верхнем и нижнем течении р. Сок не отличается между собой. Еще раз подчеркнем, что в случае рандомизационного теста нет необходимости проверять предположения о нормальности распределения выборок и равенстве их дисперсий.
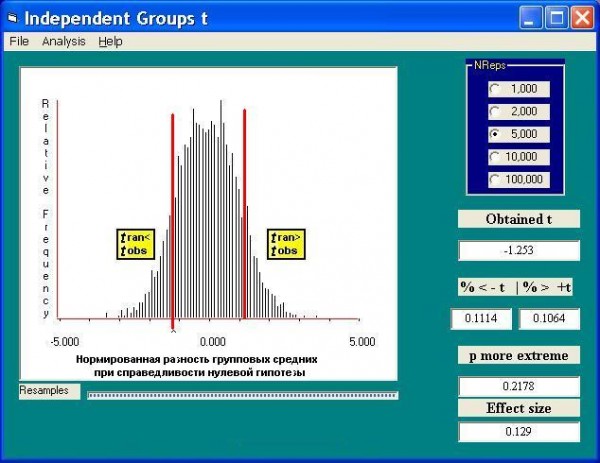
Рис. 4. Распределение t-статистики, оценивающей разность групповых средних индекса Шеннона при справедливости нулевой гипотезы. Красными линиями показано положение наблюдаемой t-статистики (Obtained t); P more extreme – вероятность превышения наблюдаемой статистики; Effect size ‒ доля эффекта от группировки данных
Fig. 4. The t-statistics distribution estimating the index Shennon Distribution group averages assuming the justice of the null-hypothesis
Аналогичные расчеты для р. Чапаевка показывают, что видовое разнообразие в верхнем течении значительно превышает этот показатель в нижнем течении. В результате 5000 перестановок 244 значений индекса Шеннона между двумя группами не нашлось ни одной такой комбинации, чтобы различия оказались бы больше, чем в реальных данных, а эмпирическая t-статистика расположилась далеко за пределами нуль-модельного распределения.
Возможна и другая схема сравнения двух групп по их медианной разности. Медиана индексов Шеннона для верхнего течения р. Чапаевки – 2.45, для нижнего – 1.6, а медианная разность групп – 0.85 (рис. 5). Случайным образом переставляя значения между группами, рассчитаем доверительные интервалы межгрупповой разности медиан при условии справедливости нулевой гипотезы. Очевидно, что эмпирическая разность медиан выходит далеко за пределы этих доверительных интервалов (±0.33), следовательно, нулевая гипотеза и здесь может быть отвергнута.
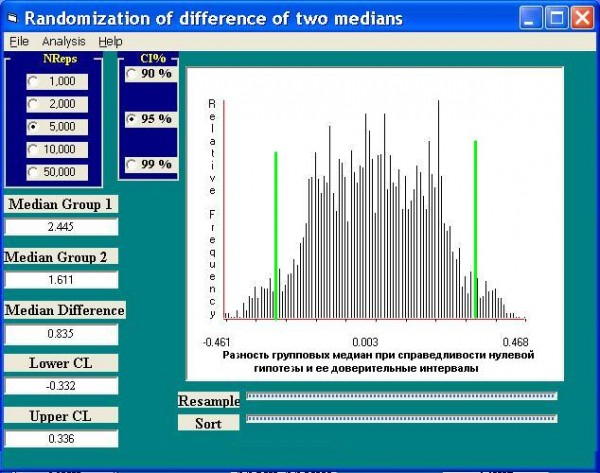
Рис. 5. Оценка доверительных интервалов медианной разности (Median Difference) двух выборок значений индекса Шеннона при справедливости нулевой гипотезы
Fig. 5. The estimation of confidential intervals differences medians of two samples of the values of the index Shennon assuming the justice of the null-hypothesis
Легко также распространить рандомизационный тест для двух независимых групп на более общий случай однофакторного дисперсионного анализа при нескольких группах. Здесь уже нельзя использовать в качестве тестовой статистики сумму значений для первой группы, межгрупповую разность средних или t-значение. Чтобы принять во внимание различия средних для всех групп, в качестве эквивалентных статистик можно использовать сумму квадратов отклонений групповых средних от глобального среднего (SSbetween) или традиционную F-метрику. Во всех остальных деталях рандомизационная процедура имеет вполне знакомые черты.
Предположим, что нам необходимо оценить влияние минерализации воды на структуру липидов многоклеточной макроводоросли Ulva intestinalis (L.) Link (Сhlorophyta). Сформируем три выборки из массовых долей (%) моногалактозилдиацилглицерола (МГДГ) по результатам анализа липидного состава в биологических пробах из малых рек Приэльтонья с различной степенью минерализации: менее 10 г/л (15 проб), от 10 до 20 г/л (25 проб) и свыше 20 г/л (15 проб). На рис. 6 можно увидеть распределение вероятности значений F, где отмечено местоположение значения F = 3.233 для эмпирических данных. Уровень значимости нулевой гипотезы p = 0.048 мы нашли путем подсчета числа итераций ресамплинга с F, большим, чем 3.233. Подчеркнем, что нам не было никакой необходимости проверять при этом нормальность распределения или равенство дисперсий в группах. Воспользовавшись любой стандартной программой дисперсионного анализа, можно легко увидеть, что найденное нами p-значение хорошо согласуется с вероятностью, полученной из теоретического F-распределения с 2 и 53 степенями свободы (что, правда, далеко не всегда будет иметь место).
Аналогичный дисперсионный анализ влияния минерализации на содержание общей суммы липидов в тканях U. intestinalis (мг/г сырой массы) в тех же условиях дал существенно более веские аргументы отклонить нулевую гипотезу: из 5000 нуль-модельных итераций не было получено ни одной комбинации, для которой имитируемая статистика превысила бы эмпирическое значение F = 14.39 (т. е. p = 0). Хотя постоянно подчеркивается, что p-значение не является «реальной и адекватной мерой статистической убедительности» (Хромов-Борисов, 2011) и их значения в разных опытах никогда не должны сравниваться, в рассмотренном случае можно предположить, что отмеченные сдвиги доли МГДГ, в первую очередь, являются «вторичным» следствием изменчивости общей массы липидов под влиянием минерализации.
Рис. 6. Распределение F-статистики, полученное методом рандомизации, для оценки влияния фактора минерализации воды на содержание липида МГДГ в ульве
Fig. 6. The F-statistics distribution received by the method of randomization for the estimation of the water mineralization factor influence to the lipid MGDG maintenance in Ulva
Применение рандомизационной процедуры к оценке линейной связи двух переменных обычно сводится к тому, что проверяется нулевая гипотеза о равенстве нулю коэффициента корреляции r = 0. Предположим, что р. Сок на всем ее протяжении от истоков до устья разбита на 13 участков, и мы хотим проанализировать изменчивость видового состава. Рассчитаем коэффициент корреляции между значениями температуры воды, которая в данном случае олицетворяет продольный градиент реки, и долей Diamesinae + Orthocladiinae в общей численности зообентоса. Для начала вычисляем коэффициент корреляции для исходных данных (он равен ‒0.68). Далее будем случайным образом перемешивать значения одной переменной относительно другой (например, температуру для участка 1 сцепим с долей диамезин для участка 7 и далее в таком же перетасованном беспорядке) и для каждой имитируемой выборки рассчитаем псевдо-коэффициент корреляции. Выполнив 5000 итераций, получим гистограмму распределения моделируемой статистики (рис. 7) при справедливости нулевой гипотезы и подсчитаем количество случаев, когда имитируемый коэффициент корреляции для рандомизированных комбинаций превысил аналогичное значение для исходной выборки.
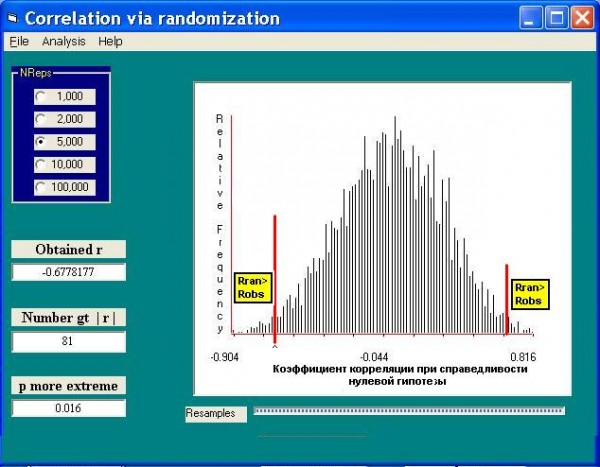
Рис. 7. Распределение коэффициента корреляции R между обилием Diamesinae + Orthocladiinae и температурой воды при нулевой гипотезе. Obtained R – значение R для исходных данных; Number gt |r| и p more extreme – соответственно частота и вероятность превышения этого значения для рандомизированных данных
Fig. 7. The distribution of the correlation factor between Diamesinae+Orthocladiinae abundance and water temperature by the null-hypothesis
Поскольку каждый x был беспорядочно связан со значениями y, то ожидаемый коэффициент корреляции на рандомизированных данных (т. е. на нуль-модели) должен быть равен 0. И только в 81 случае из 5000 нуль-модельный коэффициент корреляции превысил расчетную корреляцию для реальных наблюдений. Это означает, что исходный комплект данных отличается от рандомизированных данных, полученных при условии справедливости нулевой гипотезы, причем вероятность ошибиться в этом нашем предположении менее 1.6%. На этом основании увеличение доли диамезин по мере уменьшения температуры воды можно считать обоснованным.
4. Рандомизационные тесты для анализа видовой структуры сообществ
Поскольку коэффициент корреляции является одной из мер сходства таксономического состава местообитаний, описанную выше процедуру можно распространить на оценку любой другой метрики видового сходства (например, коэффициент Съеренсена) или, в более общем случае, на статистический анализ закономерностей в видовой структуре сообществ. Поскольку «дьявол таится в деталях», рассмотрим нетривиальные особенности этой задачи на примерах.
Пусть в результате экологических наблюдений обнаружено sa видов в сообществе a и sb видов в сообществе b, из которых sab видов оказалось общими (подмножество с). Определена также средняя популяционная плотность каждого вида i в этих подмножествах – соответственно Na(i) и Nb(i). Для оценки сходства видового состава двух биотопов a и b обычно используются две формы индекса Съеренсена-Чекановского:
° качественную 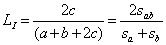 , основанную на бинарной шкале присутствия (1) или отсутствия (0) вида в сообществе (т. е. их инцидентности - incidence);
, основанную на бинарной шкале присутствия (1) или отсутствия (0) вида в сообществе (т. е. их инцидентности - incidence);
° количественную  , использующую показатели обилия особей, (другие наименования этого индекса – мера сходства Ренконена, индекс Штейнгауза, процентная разность Брея-Кертиса и проч.).
, использующую показатели обилия особей, (другие наименования этого индекса – мера сходства Ренконена, индекс Штейнгауза, процентная разность Брея-Кертиса и проч.).
При анализе индексов сходства могут быть использованы две следующие схемы рандомизации:
° обмен элементами выборок при перемешивании может происходить как между отдельными видами, так и между обоими сообществами, что соответствует нуль-модели без ограничений на рандомизацию;
° данные переставляются только в пределах каждого сообщества между отдельными его видами, т. е. значения sa, sb или суммарное обилие сравниваемых биотопов остаются в ходе пермутаций неизменными (нуль-модель с ограничениями на рандомизацию).
Тип перемешиваемых данных для реализации алгоритма роли не играет: это могут быть бинарные признаки наличия/отсутствия видов (1/0), прологарифмированные численности или частоты встречаемости видов в пробах. Для каждой пермутации вычисляется модельное значение индекса, в результате чего восстанавливается его распределение при справедливости нулевой гипотезы. На основании этого можно оценить статистическую значимость отличия реальных суперпозиций видового состава двух сообществ от случайных композиций, извлеченных из некоторого общего «резервуара» видов.
Ранее мы уже выясняли с использованием рандомизационного теста, отличается ли видовое разнообразие по Шеннону для донных сообществ верхнего (в 51 пробе было обнаружено sa = 190 видов) и нижнего (sb = 174 вида в 44 пробах) участков р. Сок. Всего в реке было обнаружено 276 видов и таксонов макрозообентоса, т. е. 88 видов было найдено одновременно на обоих участках. Вычисленные значения индекса Съеренсена-Чекановского (%) для исходных выборок (Lobs) и найденные в процессе 1000 итераций рандомизации (Lran), а также стандартное отклонение (sran), нижняя и верхняя границы 95%-х доверительных интервалов для Lran представлены в табл. 1.
Таблица 1. Статистический анализ индекса сходства биотопов по Съеренсену-Чекановскому (ДИ – доверительный интервал)
| Форма индекса | Lobs по эмпирическим данным | Тип нуль-модели | Средний Lran из 1000 итераций | Стандартное отклонение sran | Нижний уровень 95%-го ДИ | Верхний уровень 95%-го ДИ |
| Качественная LI | 48.35 | без ограничений | 65.93 | 2.01 | 62.01 | 69.86 |
| с ограничениями | 65.84 | 2.08 | 61.76 | 69.92 | ||
| Количественная LR | 42.99 | без ограничений | 30.51 | 2.28 | 26.03 | 34.99 |
| с ограничениями | 30.44 | 2.26 | 26.01 | 34.88 |
Рандомизация дает оценку не самого выборочного параметра, а его имитационной модели при условии справедливости нулевой гипотезы (т. е. для случайных композиций видов и отсутствия влияния изучаемого фактора). Поскольку индекс Съеренсена LI obs для эмпирических бинарных данных в рассматриваемом случае существенно меньше (48%), чем нуль-модельное значение LI ran (66%), то это свидетельствует о том, что различие двух списков видов больше (а сходство меньше), чем при случайном назначении видов, например, с помощью мешочка с бочонками лото. Следовательно, влияние экологических условий реки в верхнем и нижнем течении статистически значимо и это может быть объяснено продольным градиентом или особенностями речного континуума. Если бы мы имели значение эмпирического индекса сходства более 70%, то мы могли бы с уверенностью сказать, что видовой состав макрозообентоса в верховьях и в низовьях один и тот же, т. е. река представляет единое сообщество. Индекс Съеренсена LI obs в диапазоне доверительных интервалов LI ran от 62 до 70% свидетельствует о нейтральностидонного сообщества, в котором представленность видов подчинена случайным флуктуациям в однородных условиях среды, а взаимодействия между видами отсутствуют. При использовании меры Съеренсена LR для количественных данных нулевая гипотеза, по данным табл. 1, также отклоняется, поскольку корреляция популяционных плотностей видов в исходных выборках существенно выше, чем при случайном назначении. И здесь мы сталкиваемся с принципиально разной стратегией оценки видового сходства индексами этих двух типов (Шитиков и др., 2011). Индексы LI, основанные на инцидентности, оценивают сходство по всему видовому составу, делая основной акцент на комплекс редких или трудно обнаруживаемых видов, встречающихся в единичных пробах с малой численностью (таких видов в р. Сок оказалось существенное большинство). Значения «количественных» индексов LR почти целиком определяются различиями популяционной плотности небольшой (5‒10% от общего видового состава) группы ведущих таксонов-доминантов. Кроме оценки доверительных интервалов индекса Съеренсена Lran методом рандомизации при случайных композициях видов (см. табл. 1), могут быть также построены доверительные границы и для самих эмпирических значений Lobs, но уже с применением бутстреп-метода (Chao et al., 2005). Так, 95%-я доверительная область значений для LI obs оценивается от 44.1 до 52.6%, а для LR obs – от 39.2 до 46.8%. Использование этих статистических параметров будет весьма полезно при сравнении взаимного сходства видовой структуры трех или более сообществ (все сообщества так или иначе сходны между собой, но некоторые пары оказываются «сходнее»). Необходимо отметить, что использование разных способов пермутации незначительно сказалось на результатах, полученных в табл. 1, поэтому основные положения рандомизационного теста выглядят вполне убедительными, если речь идет об анализе одномерных выборок. Однако для многомерного случая эта методология сталкивается с проблемой неопределенности выбора ограничений на рандомизацию, т. е. исследователю необходимо предварительно оценить степень «вольности», с которой будут перемешиваться данные, и задать механизм перестановок, адекватный поставленной задаче. Пусть мы имеем матрицу наблюдений X, значениями которой Xij (i = 1, 2, …, s; j = 1, 2, …, m) являются признаки встречаемости s различных видов для каждого из m исследованных экологических объектов (участков рек, биотопов, местообитаний). Ограничимся также представлением данных в альтернативной шкале: 1 – наличие вида, 0 – его отсутствие. Зададимся целью проверить нулевую гипотезу о случайном характере формирования матрицы X, т. е. между видами отсутствует какая-либо взаимосвязь (вероятность их совместного появления или взаимного исключения соответствует стохастическому процессу). Альтернативная гипотеза сводится к предположению, что метаструктура таблицы наблюдений определенным образом детерминирована и конфигурация ее отдельных фрагментов не может быть интерпретирована как случайность. Биологической причиной такой детерминированности могут быть как межвидовые взаимодействия (наличие конкуренции за пищевые ресурсы, отношения «хищник – жертва», кооперация или мутуализм), так и эффект пространственной неоднородности (Шитиков, Зинченко, 2011). Наиболее характерные типы структурной организации матрицы X представлены на рис. 8.
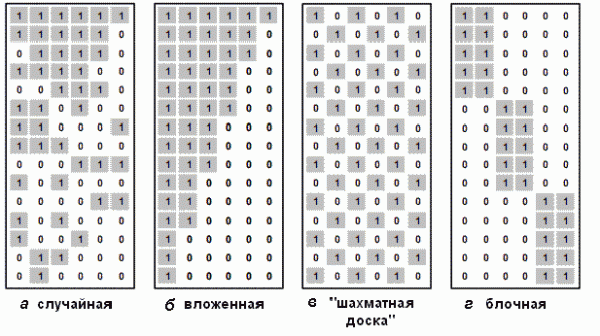
Рис. 8. Наиболее характерные типы структурной организации сообществ
Fig. 8. The most typical structural organizations of communities: (a) random, (b) nested, (c) checkerboard, (d) block
Рассмотрим одну из возможных метрик, которую мы будем использовать для проверки нулевой гипотезы. Если использовать известное положение теории вероятности о том, что общая суммарная дисперсия нескольких случайных величин равна сумме дисперсий каждой из них плюс удвоенная сумма ковариаций, то на основе данных в столбцах таблицы можно записать: 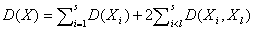 . Компоненты разложения дисперсии в общем случае неизвестны, но могут быть рассчитаны по результатам наблюдений. Пусть выборочная оценка D(Xi) равна
. Компоненты разложения дисперсии в общем случае неизвестны, но могут быть рассчитаны по результатам наблюдений. Пусть выборочная оценка D(Xi) равна 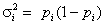 , где pi – средняя встречаемость i-го вида в обследованных объектах, pi = ni/n, а оценка D(X) общей дисперсии появления всех видов –
, где pi – средняя встречаемость i-го вида в обследованных объектах, pi = ni/n, а оценка D(X) общей дисперсии появления всех видов – 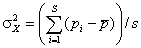 , где
, где 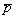 – наблюдаемая средняя встречаемость одного вида в одном местообитании. Нулевая гипотеза (H0) об отсутствии сопряженности между видами справедлива, если сумма ковариаций D(Xi, Xj) равна нулю. Это будет верно, когда виды независимо распределены в таксономических композициях представленных биотопов, но также может иметь место, если положительные и отрицательные ковариации уравновешивают друг друга. Если проверять H0 против альтернативы, что есть чисто положительная или чисто отрицательная зависимость между видами, то, при справедливости H0, имеет место отношение
– наблюдаемая средняя встречаемость одного вида в одном местообитании. Нулевая гипотеза (H0) об отсутствии сопряженности между видами справедлива, если сумма ковариаций D(Xi, Xj) равна нулю. Это будет верно, когда виды независимо распределены в таксономических композициях представленных биотопов, но также может иметь место, если положительные и отрицательные ковариации уравновешивают друг друга. Если проверять H0 против альтернативы, что есть чисто положительная или чисто отрицательная зависимость между видами, то, при справедливости H0, имеет место отношение 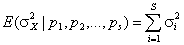 . Следовательно, дисперсионное отношение Шлютера
. Следовательно, дисперсионное отношение Шлютера 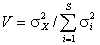 может служить обобщенным «индексом взаимозависимости» видов в матрице наблюдений (Schluter, 1984). Если H0 верна, то ожидаемое значение V = 1. Значение V, большее или меньшее 1, указывает, что между видами в местообитаниях есть статистическое положительное или отрицательное взаимодействие. Термин «статистическое» употреблен нами, чтобы подчеркнуть частный характер таких связей: например, на фоне нейтральных взаимоотношений между большинством видов может оказаться одна или несколько пар видов-»антагонистов», редко встречающихся совместно. Если предположить, что для эмпирических данных справедлива центральная предельная теорема, то при достаточно больших значениях m и s последовательности pi можно интерпретировать как независимые случайные величины, приблизительно распределенные по нормальному закону. Тогда индекс взаимозависимости показателей V при справедливости H0 будет иметь c2-распределение с m степенями свободы, а критические значения для того, чтобы отклонить нулевую гипотезу, определяются пределами табличных значений, например:
может служить обобщенным «индексом взаимозависимости» видов в матрице наблюдений (Schluter, 1984). Если H0 верна, то ожидаемое значение V = 1. Значение V, большее или меньшее 1, указывает, что между видами в местообитаниях есть статистическое положительное или отрицательное взаимодействие. Термин «статистическое» употреблен нами, чтобы подчеркнуть частный характер таких связей: например, на фоне нейтральных взаимоотношений между большинством видов может оказаться одна или несколько пар видов-»антагонистов», редко встречающихся совместно. Если предположить, что для эмпирических данных справедлива центральная предельная теорема, то при достаточно больших значениях m и s последовательности pi можно интерпретировать как независимые случайные величины, приблизительно распределенные по нормальному закону. Тогда индекс взаимозависимости показателей V при справедливости H0 будет иметь c2-распределение с m степенями свободы, а критические значения для того, чтобы отклонить нулевую гипотезу, определяются пределами табличных значений, например: 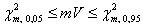 . Однако предположения о нормальности распределения вероятностей появления видов привели к тому, что дисперсионный тест Шлютера в его оригинальной версии оказался чрезвычайно чувствителен к таксонам с высокой частотой и склонен к гипердиагностике взаимосвязи. Для решения этих проблем были разработаны имитационные процедуры рандомизации путем многократного случайного перемешивания матриц наблюдения (Gotelli, 2000). Анализ статистических закономерностей структурой организации сообществ можно также выполнять, не прибегая к теоретико-вероятностным представлениям. Например, индекс заполнения шахматной доски (Checkerboard score – Stone, Roberts, 1990), оценивает среднее число подматриц
. Однако предположения о нормальности распределения вероятностей появления видов привели к тому, что дисперсионный тест Шлютера в его оригинальной версии оказался чрезвычайно чувствителен к таксонам с высокой частотой и склонен к гипердиагностике взаимосвязи. Для решения этих проблем были разработаны имитационные процедуры рандомизации путем многократного случайного перемешивания матриц наблюдения (Gotelli, 2000). Анализ статистических закономерностей структурой организации сообществ можно также выполнять, не прибегая к теоретико-вероятностным представлениям. Например, индекс заполнения шахматной доски (Checkerboard score – Stone, Roberts, 1990), оценивает среднее число подматриц 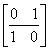 и
и 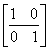 размерностью 2 * 2 для произвольной пары видов i и j:
размерностью 2 * 2 для произвольной пары видов i и j: 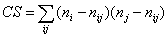 , где ni и nj – частоты их встречаемости, nij – одновременная встречаемость каждой пары видов. Индекс изменяется в диапазоне от 0 до
, где ni и nj – частоты их встречаемости, nij – одновременная встречаемость каждой пары видов. Индекс изменяется в диапазоне от 0 до 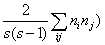 . Существует достаточно большой набор взглядов на способы конструирования алгоритмов рандомизации матриц, поэтому существенной проблемой статистического анализа статистик V и CS является выбор вычислительной процедуры генерации нуль-модели с теми или иными ограничениями на перебор. «Равновероятные» EE (Equiprobable) алгоритмы осуществляют перестановку значений в пределах исходной матрицы без каких-либо ограничений и сохраняют минимальное количество информации, содержащейся в исходных данных. В противоположность этому наименее «либеральная» дважды фиксированная модель FF (Fixed-Fixed) требует, чтобы общая встречаемость «единиц» в строках и столбцах нуль-матрицы соответствовала бы наблюдаемым значениям в эмпирической матрице. Комбинированная модель EF (Equiprobable-Fixed) сохраняет неизменным число видов для каждого объекта, но позволяет частотам появления признаков (т. е. общему количеству единиц в строках) изменяться беспорядочно и равновероятно. Модель FE (Fixed-Equiprobable) делает то же самое в отношении столбцов (т. е. объектов). Разработана также коллекция пропорциональных (Proportional) моделей P, которые в процессе перебора отдают предпочтение тем или иным видам согласно вероятности их встречаемости, а также пропорционально абсолютным значениям их численности либо иным популяционным параметрам. В теоретическом плане становится все более ясным, что статистические тесты, которые используют полностью равновероятные нуль-модели EE, не вполне соответствуют практическому смыслу стохастичности (Gotelli, McGill, 2006). Идеальная нуль-модель должна обладать как хорошей мощностью идентифицировать истинные закономерности, если взаимосвязи между признаками имеют неслучайный характер, так и не обнаруживать статистической значимости эффекта в матрицах, где распределение показателей сгенерировано стохастическим процессом. Сформируем матрицу по данным 51 гидробиологической пробы, выполненных в разных точках верхнего течения р. Сок, в которых было обнаружено всего 190 видов донных организмов. Если в появлении этих видов есть определенная закономерность, то эмпирическая матрица X размером 190 ´ 51 по выбранному критерию E статистически значимо отличается от нуль-модельных матриц, в которых комбинации видов хаотически перемешаны. Проверка статистических гипотез (a = 0.05) проводилась с использованием Z-критерия
. Существует достаточно большой набор взглядов на способы конструирования алгоритмов рандомизации матриц, поэтому существенной проблемой статистического анализа статистик V и CS является выбор вычислительной процедуры генерации нуль-модели с теми или иными ограничениями на перебор. «Равновероятные» EE (Equiprobable) алгоритмы осуществляют перестановку значений в пределах исходной матрицы без каких-либо ограничений и сохраняют минимальное количество информации, содержащейся в исходных данных. В противоположность этому наименее «либеральная» дважды фиксированная модель FF (Fixed-Fixed) требует, чтобы общая встречаемость «единиц» в строках и столбцах нуль-матрицы соответствовала бы наблюдаемым значениям в эмпирической матрице. Комбинированная модель EF (Equiprobable-Fixed) сохраняет неизменным число видов для каждого объекта, но позволяет частотам появления признаков (т. е. общему количеству единиц в строках) изменяться беспорядочно и равновероятно. Модель FE (Fixed-Equiprobable) делает то же самое в отношении столбцов (т. е. объектов). Разработана также коллекция пропорциональных (Proportional) моделей P, которые в процессе перебора отдают предпочтение тем или иным видам согласно вероятности их встречаемости, а также пропорционально абсолютным значениям их численности либо иным популяционным параметрам. В теоретическом плане становится все более ясным, что статистические тесты, которые используют полностью равновероятные нуль-модели EE, не вполне соответствуют практическому смыслу стохастичности (Gotelli, McGill, 2006). Идеальная нуль-модель должна обладать как хорошей мощностью идентифицировать истинные закономерности, если взаимосвязи между признаками имеют неслучайный характер, так и не обнаруживать статистической значимости эффекта в матрицах, где распределение показателей сгенерировано стохастическим процессом. Сформируем матрицу по данным 51 гидробиологической пробы, выполненных в разных точках верхнего течения р. Сок, в которых было обнаружено всего 190 видов донных организмов. Если в появлении этих видов есть определенная закономерность, то эмпирическая матрица X размером 190 ´ 51 по выбранному критерию E статистически значимо отличается от нуль-модельных матриц, в которых комбинации видов хаотически перемешаны. Проверка статистических гипотез (a = 0.05) проводилась с использованием Z-критерия 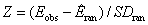 и на основе границ интервалов, соответствующих 95%-й доверительной вероятности. Приведенные в табл. 2 результаты показывают, что итоговые выводы в многомерном случае сильно зависят от принятых ограничений на рандомизацию и выбранной нуль-модели: для EF, FE и EE нулевая гипотеза об отсутствии межвидовых взаимодействий отклоняется, в то время как они принимаются статистически незначимыми в некоторых случаях использования моделей P и FF.
и на основе границ интервалов, соответствующих 95%-й доверительной вероятности. Приведенные в табл. 2 результаты показывают, что итоговые выводы в многомерном случае сильно зависят от принятых ограничений на рандомизацию и выбранной нуль-модели: для EF, FE и EE нулевая гипотеза об отсутствии межвидовых взаимодействий отклоняется, в то время как они принимаются статистически незначимыми в некоторых случаях использования моделей P и FF.
Таблица 2. Статистический анализ двух индексов структурированности сообществ макрозообентоса р. Сок (ДИ – доверительный интервал)
| Наиме нование тестовой статис тики E | Eobs по эмпирическим данным | Тип нуль-модели | Среднее Eran из 100 итераций | Стандартное отклонение sran | Z-статистика | Нижний уровень 95%-го ДИ | Верхний уровень 95%-го ДИ |
| Заполнение шахматной доски (CS) | 7.29 | (P) Пропорционально частотам | 6.44 | 0.19 | 4.45 | 6 | 6.78 |
| (FF) Фиксируются суммы строк и столбцов | 7.22 | 0.04 | 1.51 | 7.15 | 7.32 | ||
| (FE) Фиксируются суммы строк | 7.67 | 0.04 | -9.51 | 7.58 | 7.74 | ||
| (EF) Фиксируются суммы столбцов | 9.4 | 0.05 | -45.08 | 9.3 | 9.49 | ||
| (EE) Равновероятная модель | 9.66 | 0.04 | -61.08 | 9.58 | 9.72 | ||
| Дисперсионный тест Шлютера (V) | 7.96 | (P) Пропорционально частотам | 8.59 | 0.79 | -0.8 | 7.18 | 10.46 |
| (FF) Фиксируются суммы строк и столбцов | 7.96 | 0 | 0 | 7.96 | 7.96 | ||
| (FE) Фиксируются суммы строк | 8.05 | 0.01 | -18.45 | 8.04 | 8.07 | ||
| (EF) Фиксируются суммы столбцов | 54.05 | 5.94 | -7.75 | 44.17 | 67.81 | ||
| (EE) Равновероятная модель | 54.57 | 5.07 | -9.19 | 45.07 | 63.3 |
Все представленные выше имитационные процедуры с различными схемами генерации нуль-моделей можно ранжировать в ряд по мере снижения ограничений на рандомизацию: FF > P > (EF, FE) > EE. В этом же направлении увеличивается уровень ошибки 1-го рода (т. е. анализ становится менее консервативным) и нулевая гипотеза будет отклоняться, даже если взаимосвязь между признаками выглядит весьма сомнительно. Однако в этом же ряду уменьшается ошибка 2-го рода (принятие ложной нулевой гипотезы), поэтому предпочтение часто отдается моделям типа EF. Согласно другим рекомендациям, в условиях пассивного формирования выборок более надежные результаты дают модели FF и P.
Заключение
В каких случаях целесообразно применять ресамплинг, а в каких ‒ другие обычные статистические методы? Если верны исходные предположения (например, о нормальности распределения результатов наблюдений), то при достаточном числе испытаний Монте-Карло бутстреп-оценка параметров и р-значение, полученное при рандомизации, очень близки к классическим оценкам – см. примеры, связанные с рис. 1 и 6. Это дало повод высказать категорическое мнение о бесполезности бутстрепа: «там, где найдены методы анализа данных, в том или ином смысле близкие к оптимальным, бутстрепу делать нечего» (Орлов, 2002). Однако совпадение результатов или выводов является как раз свидетельством верности идеологии рандомизации и бутстрепа, а моделируемое распределение искомой статист ики в ходе повторной генерации выборок добавляет к анализу наглядности и убедительности. Если же обрабатываются данные, статистические свойства которых недостаточно ясны, или мы имеем дело со сложными системами с нетривиальным характером взаимодействий, ресамплинг представляет собой ценный инструмент для изучения ситуации.
Еще раз подчеркнем фундаментальное различие между рандомизацией и бутстрепом: если рандомизационный тест применяется, чтобы оценить степень упорядоченности структуры данных или взаимосвязи между отдельными ее фрагментами, то бутстреп, или «складной нож», используется для получения наиболее корректной оценки параметров распределения случайной величины (среднего, медианы, дисперсии и т. д.). В частности, при подсчете обычной выборочной статистики (например, среднего) порядок следования элементов выборки не имеет значения, и каждая итерация перестановок будет возвращать одну и ту же величину, т. к. сами по себе данные в ходе пермутаций не изменяются. Возможность гибкой настройки и использование идей самоорганизации отличает бутстреп от метода «складного ножа» с его параметризованным и менее интенсивным вычислительным подходом. Вместе с тем алгоритмы jackknife нашли в экологии широкое применение для прогнозирования числа «невидимых» редких видов и экстраполяции видового богатства сообщества (см. обзор Шитикова и др., 2010), т. е. оценки того, сколько видов может быть обнаружено в исследуемой области, если количество выполненных проб будет увеличено, например, вдвое.
Вопрос о полной теоретической корректности методов ресамплинга остается открытым. Например, математики не пришли пока к единому мнению относительно таких проблем бутстрепа, как рецентрирование, эффективность корректировки смещения, процедуры построения доверительных интервалов и т. д. Нельзя не отметить низкую эффективность бутстрепа при недостаточной репрезентативности исходного массива наблюдений, когда начинают генерироваться сходные псевдовыборки с микроскопическим сдвигом корректируемого параметра. Есть много различных путей развития идей размножения выборок (Орлов, 2002), чтобы внести в переборную стохастику некоторое зерно детерминизма. Можно, например, по исходной выборке построить эмпирическую функцию распределения, а затем тем или иным образом от кусочно-постоянной функции перейти к непрерывной функции распределения, например соединив точки [x(i); i/n], i = 1, 2, …, n, отрезками прямых. Другой вариант построения размноженных выборок – к исходным данным добавляются малые независимые одинаково распределенные погрешности (при таком подходе одновременно соединяются вместе идеи устойчивости и бутстрепа).
Не менее серьезные трудности начинаются, когда мы практически сталкиваемся с тонкостями отдельных ситуаций, чтобы корректно проверить статистическую гипотезу, качественно устранить сдвиг и/или скомпенсировать неустойчивость конкретного параметра. В значительной мере ресамплинг к настоящему времени представляет собой сборник «разнокалиберных» алгоритмов, статистические свойства которых по отношению к различным объектам данных являются недостаточно изученными. Это убедительно демонстрирует приведенный нами пример с неопределенностью выбора ограничений на рандомизацию при создании нуль-модели (см. табл. 2). Справедливости ради имеет смысл напомнить, что история широкого использования параметрических методов в статистике насчитывает полторы сотни лет, тогда как о ресамплинге всего 20 лет назад знали лишь узкие специалисты.
Главная трудность недостаточного практического использования процедур рандомизации и бутстрепа сводится к необходимости иметь необходимое программное обеспечение. Хотя сами методики расчета концептуально очень просты, тем не менее у вас должен быть доступный программный модуль, позволяющий осуществить генерацию повторных выборок. В частности, нам не удалось найти внятных возможностей использовать бутстреп-процедуры во многих важных пунктах анализа данных в необычайно, хотя и незаслуженно, популярном пакете Statistica 8.
Ф. Гуд (Good, 2006) в своем практическом руководстве по применению методов ресамплинга при анализе данных рассматривает два подхода:
- использование макроопределений статистических пакетов, таких как MatLab, SAS, Stats, а также непосредственное программирование в средах Visual Basic, C++, Delphi;
- использование программ, управляемых с помощью меню, таких как S-Plus, Stata, StatXact, SYSTAT или Testimate.
В ряде случаев анализ реализуется комбинированным способом: через меню и с использованием системы команд, что является наиболее рациональным. Гуд приводит коллекцию избранных текстов модулей на языках C++ и SAS, список макросов обращений к внутренним компонентам в средах Eviews, MatLab, Resampling Stats, R, S-Plus, Stata, а также дает описание расширения Resampling Stats Excel Add-in.
Поскольку некоторые перечисленные программные комплексы весьма недешевы, рекомендуем обратить внимание на компактные версии очень удобных, бесплатных и «биологически ориентированных» программ, созданных усилиями следующих авторов:
- П. Ядвижчака (P. Jadwiszczack, http://pjadw.tripod.com/), который разработал превосходную программу RundomPro 3.14 с большими возможностями использования классических и современных методов статистики; этот пакет можно порекомендовать, в первую очередь, продвинутым пользователям, поскольку описание методов оформлено в виде ссылок на фундаментальную монографию Б. Манли (Manly, 2007);
- проф. Д. Хауэлла (D. Howell, http://www.uvm.edu/~dhowell/StatPages/Resampling/), который уже был представлен выше вместе с его программой Resampling Procedures;
- Б. Рипли (B. D. Ripley), К. Халворсена (K. Halvorsen), А. Канти (A. J. Canty) и других разработчиков пакетов для бесплатной статистической среды R (www.r-project.org), с помощью которой, если взять на себя труд разобраться в достаточно простом макроязыке, можно делать буквально все мыслимые статистические вычисления в биологии;
- Ф. Хаммера и др. (Ø. Hammer, D. Harper, P. Ryan, http://folk.uio.no/ohammer/past), разработавших прекрасный набор разнообразных статистических функций для анализа палеонтологических (читай ‒ «экологических») данных PAST, где активно представлено уточнение выборочных параметров бутстреп-методом. Весьма полезными для освоения ресамплинга могут быть материалы сайта «Resampling Stats» (http://www.resample.com), который поддерживается Дж. Саймоном и П. Брюсом (J. Simon and P. Bruce), где можно найти книги, статьи, учебные курсы, программные модули и ссылки на другие родственные сайты.
Возможности использования методов ресамплинга выходят далеко за рамки примеров, представленных выше. Точно также неисчерпаемы и конкретные проблемы количественной гидроэкологии, которые можно обосновать с использованием этих методов. Здесь можно отметить различные версии многомерного дисперсионного анализа, подбор наилучшей регрессии, анализ таблиц сопряженности, построение иерархических деревьев и т. д. Описание этих методов детально представлено в приведенных литературных источниках.
Библиография
Анатольев С. Основы бутстрапирования // Квантиль. 2007. № 3. С. 1‒12. URL: http://quantile.ru/03/N3.htm (дата обращения: 29.12.2011).
Мостеллер Ф., Тьюки Дж. Анализ данных и регрессия. М: Финансы и статистика, 1982. Вып. 1. 320 с.
Орлов А. И. Эконометрика. М.: Экзамен, 2002. 576 с. URL: http://orlovs.pp.ru (дата обращения: 29.12.2011).
Хромов-Борисов Н. Н. Синдром статистической снисходительности или значение и назначение p-значения // Телеконференция по медицине, биологии и экологии, 2011. № 4. URL: http://tele-conf.ru/aktualnyie-problemyi-tehnologicheskih-izyiskaniy/3.html (дата обращения: 29.12.2011).
Шитиков В. К., Зинченко Т. Д. Анализ статистических закономерностей организации видовой структуры донных речных сообществ // Журнал общей биологии. 2011. Т. 72. № 5. С. 355–368.
Шитиков В. К., Зинченко Т. Д., Абросимова Э. В. Непараметрические методы сравнительной оценки видового разнообразия речных сообществ макрозообентоса // Журнал общей биологии. 2010. Т. 71. № 3. С. 263‒274.
Шитиков В. К., Зинченко Т. Д., Розенберг Г.С. Макроэкология речных сообществ: концепции, методы, модели. Тольятти: СамНЦ РАН, Кассандра, 2011. 255 с. URL: http://www.ievbras.ru/ecostat/Kiril/Download/Maec.pdf (дата обращения: 29.12.2011).
Шитиков В. К., Розенберг Г. С., Крамаренко С. С., Якимов В. Н. Современные подходы к статистическому анализу экспериментальных данных // Проблемы экологического эксперимента (Планирование и анализ наблюдений). Тольятти: СамНЦ РАН, Кассандра, 2008. С. 212‒250. URL: http://www.ievbras.ru/ecostat/Kiril/Download/Mepe.pdf (дата обращения: 29.12.2011).
Эфрон Б. Нетрадиционные методы многомерного статистического анализа. М.: Финансы и статистика, 1988. 263 с.
Chao A., Chazdon R. L., Colwell R. K., Shen T. J. A new statistical approach for assessing similarity of species composition with incidence and abundance data // Ecol. Letters. 2005. Vol. 8. P. 148‒159.
Chernick M. R. Bootstrap methods, a practitioner's guide. Wiley Series in Probability and Statistics, 1999. 369 p.
Chernick M.R., Fritis R. Introductory biostatistics for the health sciences: modern applications including bootstrap. Wiley Series in Probability and Statistics, 2003. 406 p.
Davison A. C., Hinkley D. V. Bootstrap methods and their application. Cambridge: Cambridge University Press, 2006. 592 p.
Edgington E. S. Randomization tests. N. Y.:Marcel Dekker, 1995. 341 p.
Efron B. Bootstrep methods. Another look at the Jacknife // Ann. Statist. 1979. № 7. P. 1‒26.
Efron B., Tibshirani R. J. An introduction to the bootstrap. N. Y.: Chapman & Hall, 1993. 436 p.
Good P. Permutation, parametric and bootstrap tests of hypotheses. N.Y.: Springer, 2005. 315 p.
Good P. Resampling Methods: a practical guide to data analysis. N.Y.: Springer, 2006. 218 p.
Gotelli N. J. Null model analysis of species co-occurrence patterns // Ecology. 2000. Vol. 81. P. 2606‒2621.
Gotelli N. J., McGill B. J. Null versus neutral models: what’s the difference? // Ecography. 2006. Vol. 29. P. 793‒800.
Howell D. Resampling Statistics: Randomization and the Bootstrap. URL: http://www.uvm.edu/~dhowell/StatPages/Resampling/Resampling.html (Last revised: 31.3.2007)
Lunneborg C. E. Data analysis by resampling: Concepts and applications. Pacific Grove, CA: Duxbury, 2000. 568 p.
Manly B. F. J. Randomization, bootstrap and Monte Carlo methods in biology. London: Chapman & Hall, 2007. 445 p.
Mooney C. Z., Duval R. D. Bootstrapping. A nonparametric approach to statistical inference. Sage,CA: University paper, 1993. 80 p.
Rubinstein R. Y., Kroese D. P. Simulation and the Monte Carlo Method. John Wiley & Sons, 2003. 336 p.
Simon J. L. Resampling: the new statistics. Arlington, Virginia: Resampling Stats, 1997. 209 p.
Schluter D. A variance test for detecting species associations, with some example applications // Ecology, 1984. Vol. 65. P. 998–1005.
Tukey J. W. Bias and confidence in not quite large samples // Ann. Math. Statist. 1958. Vol. 29. P. 614.






 © 2011 - 2026
© 2011 - 2026