Коросов А. В., Киреева М. Л., Гусева Т. Л. Опыт фрактального анализа населения микромаммалий мозаичных ландшафтов Карелии // Принципы экологии. 2015. № 4. С. 35–47. DOI: 10.15393/j1.art.2015.4741

Выпуск № 4

Оригинальные исследования

pdf-версия статьи

574.472

Опыт фрактального анализа населения микромаммалий мозаичных ландшафтов Карелии

Введение

Фрактал – это структура, состоящая из частей, которые в каком-то смысле подобны целому (Федер, 1991). Самоподобие геометрической фигуры выявляется при изменении масштаба исследования – в процессе рассмотрения все меньших и меньших фрагментов объекта эти части в определенном смысле оказываются подобными целому. Природные сообщества могут рассматриваться как стохастические фракталы и при разных размерах могут демонстрировать подобие статистических характеристик (Гелашвили и др., 2013). Если показатели структуры видового сообщества на небольшой площади в определенном смысле подобны структуре сообществ на большей территории, то такую организацию можно назвать фрактальной, ею обладают многие виды в естественных местообитаниях. Как фрактальность структуры сообществ, так и случаи ее нарушения составляют предмет экологических исследований.

Цель сообщения состоит в том, чтобы на примере сообществ мелких млекопитающих средней тайги Карелии рассмотреть применимость мультифрактального анализа для исследования закономерностей пространственного распределения животных и попытаться выявить проблемы, возникающие при описании натурных наблюдений средствами мультифрактального анализа.

Материалы

В работе использованы материалы учета численности и видового состава мелких млекопитающих на участке площадью около 10 кв. км в окрестностях д. М. Гомсельга (Кондопожский р–н, Карелия). На основе дешифрирования космоснимков и полевой съемки построена карта для девяти типов местообитаний животных (Гусева и др., 2014). В их числе (рис. 1: 1–9) верховые сфагновые болота (1), луга (бывшие пашни, 2) и серия стадии сукцессии фитоценозов средней тайги – свежие вырубки, покрытые травой (1–2 года после рубок, 3), молодые вырубки, поросшие кустарником (3–7 л., 4), жердняки (7-11 л., 5), молодые лесные сообщества (в изученном районе – только лиственные, 12–17 л., 6), лиственные леса (18-70 л., 7), смешанные леса (70–100 л., 8), хвойные леса (почти исключительно сосняки, более 100 л., 9). Вследствие длительной истории освоения региона описанные типы местообитания имеют примерно равные площади, образуя очень неоднородную, пеструю среду обитания для животных, которая постоянно претерпевает все новые вмешательства человека.

  

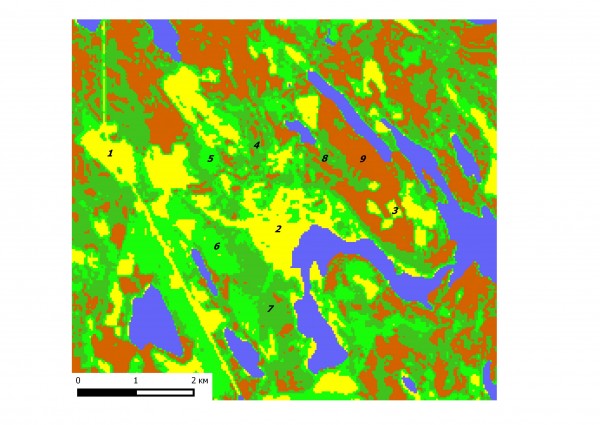
Рис. 1. Мозаика 9 типов биотопов (водные объекты – голубые) на дешифрированном космоснимке района работ (июль 2001 г.)

 Fig. 1. Mosaic of 9 types of habitats (water bodies are blue) on the decoded space image of the studied area (July 2001)

 

В период с 1996 по 2015 гг.  выполнен отлов в 529 линий ловушек. Всего отработано 61559 давилко–суток, отловлено 4278 особей 13 видов зверьков (Clethrionomys glareolus, Microtus agrestis, Microtus oeconomus, Micromys minutus, Sorex araneus, Sorex isodon, Sorex caecutiens, Sorex minutus, Sicista betullina, Neomys fodiens, Talpa europae , Arvicola terrestris, Clethrionomys rutilus ). В работе нами использовались данные отлова только в августе месяце (для 20 лет): отработано 16126 давилко–суток, поймано 2043 особи 11 видов. В анализе использовались следующие обозначения: N – общее число отловленных животных (принято в качестве меры масштаба), p_ij – доля особей i-го вида в j-й выборке.

Для проведения мультифрактального анализа было выполнено агрегирование данных и составлено 66 выборок на основе общей выборки животных. Исходная группа состоит из 56 выборок, относящихся к «локалитетам» – площадкам многолетнего отлова. Каждая из выборок этой группы включает животных, отловленных в разные годы на одной площадке. Отдельная площадка целиком включена в один тип биотопа. Площадки отстоят друг от друга на сотни метров и километры и каждый тип биотопа представлен несколькими площадками (от 4 до 12). Вторая группа состоит из 9 выборок, объединяющих выборки для каждого из изученных типов биотопов. Еще одна общая выборка объединяет все выборки в регионе. В итоге была получена матрица, состоящая из 66 выборок (рядов значений p_ij).

Методы

Мультифрактальный анализ выполнялся в соответствии с опубликованными рекомендациями (Гелашвили и др., 2013). Алгоритм состоит из четырех крупных и серии промежуточных процедур количественной обработки данных.

I. Подготовить стратифицированные выборки (см. выше).

II. Рассчитать серию рабочих переменных (q, M_q, logM_q, logN, F, AIC, t_q , a_т, F(a), D):

1. сформировать исходную матрицу данных размером S*k (S – число видов, k – количество выборок)
2. выбрать масштабную переменную N (например, число особей всех видов)
3. рассчитать значения доли i–го вида в j–той выборке p_ij = N_i / N_j
4. выбрать шаг для приращения степени q
5. рассчитать значения моментов M_q(N) для каждого q 
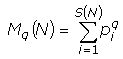
6. рассчитать logM_q, logN и построить графики зависимости между ними
7. оценить линейность этих зависимостей (в отличие от рекомендаций, мы использовали критерий F Фишера)
8. рассчитать скорость изменения моментов t_q как коэффициент регрессии по значениям для всех выборок: logM_q = t_q logN_q+ b

III. Построить график мультифрактального спектра:

1. рассчитать индекс сингулярности a_q = –((t_q+h – t_q–h) / 2h)) (В монографии (Гелашвили и др., 2013) расчетная формула индекса сингулярности на стр. 141 записана с ошибкой – отсутствует знак минуса.)
2. рассчитать значения функции мультифрактального спектра f_a = q*a_q + t_q
3. построить график мультифрактального спектра – график зависимости f_a от а

IV. Дать интерпретацию мультифрактальному спектру в соответствии с рекомендациями (Гелашвили, 2011).

Выборки формировались и корректировались в среде  MS Access  и MS Excel. Расчеты по алгоритму анализа выполнены в среде R (скрипт).

Результаты

 Из 11 видов зверьков, отловленных в августе, доминирующие позиции занимают обыкновенная бурозубка (S. araneus) и рыжая полевка (Cl. glareolus). Реже встречается пашенная полевка (M. agrestis ), малая бурозубка (S. minutus ), равнозубая бурозубка (S. isodon ). В разных биотопах структура доминирования неодинакова. Например, в хвойном лесу доминирующим видом является рыжая полевка (49%), субдоминантом обыкновенная бурозубка (41%), в молодом лиственном лесу доминант обыкновенная бурозубка (67%), субдоминант рыжая полевка (27%) (рис. 2). Остальные виды в обоих сообществах представлены хуже – их суммарная доля составила менее 3%.

 

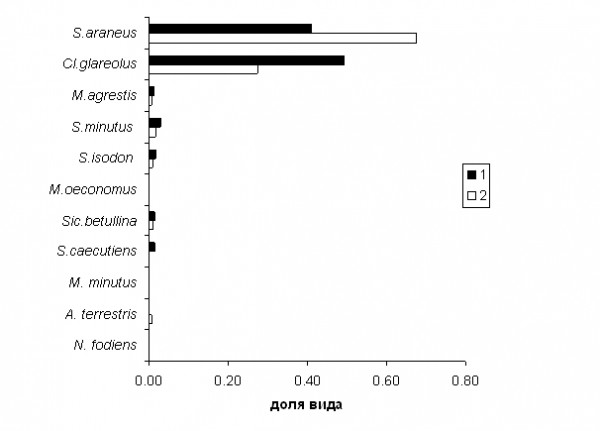
Рис. 2. Структура сообществ мелких млекопитающих в августе: 1 – хвойный лес, 2 – молодой лиственный лес

 Fig. 2. The structure of small mammal's community in August: 1 - coniferous forest, 2 - young leaf forest

 

Дальнейший анализ будем проводить, приняв в качестве меры масштаба объем выборки – общее число отловленных особей, N.

Для расчета моментов M назначили диапазон значений степени q от – 3 до 3 и составили ряды с шагом от 0.4 до 0.75 в разных вариантах рассчетов.

Для каждой из 66 сформированных выборок были рассчитаны моменты M_q – сумма долей всех видов в степени q. Значение M_q – это компактная характеристика структуры видового сообщества, зависящая от величины показателя q. Некоторые значения M_q имеют простую интерпретацию. Значение доли вида, возведенное в степень 1 (q = 1), не меняется, поэтому сумма долей, возведенных в степень 1, дает простую сумму долей всех видов в одной выборке, равную единице, M₁ = 1. Возведение в степень 0 любое число превращает в единицу, поэтому  M₀ (Sp_i⁰) равно количеству видов в выборке. Другие значения q сообщают значениям M_q особенные свойства. Значения q больше 1 усиливают вклад в значение M_q доминирующих видов, поскольку возведение в положительные степени сильнее меняет большие значения, нежели малые. Отрицательные значения q – это обратные величины от доли вида p^–q = 1/p^q и поэтому резко снижают долю доминантов в показателе M_q, усиливая вклад редких видов в величину M_q для данной выборки (Артюшенко и др., 2011).

Для иллюстрации приведем пример расчета четырех значений M  (q =– 2, 0, 1, 2) для первого локалитетата из первого биотопа (табл. 1). Так, M₀ = 4 – в сообществе всего четыре вида; M₂ = 0.66, M_–2 =14479. Сравнение с ними значения для шестого локалитета (один тип биотопа  – см. табл. 2): M₂ = 0.56, M_–2 = 39922 показывает, что роль доминатов в этом локалитете несколько ниже, чем первом, но роль редких видов выше. Это понятно, поскольку в силу большего объема «промысловых усилий» на шестой площадке удалось отловить больше видов (6 против 4).

 

Таблица 1. Исходные данные и этапы расчета моментов для площадки (локалитета) 1 из биотопа 1 (молодой лес) 

вид	ni	pi	pi–2	pi0	pi1	pi2
S. isodon	1	0.0118	7225	1	0.01	0.0001
S. minutus	1	0.0118	7225	1	0.01	0.0001
Cl. glareolus	16	0.1882	28.2226	1	0.19	0.0354
S. araneus	67	0.7882	1.6095	1	0.79	0.6213
Mq = Σ piq	85	1	M-2 = 14479	M0 = 4	M1 = 1	M2 = 0.66

 

 Таблица 2. Сводная таблица расчета моментов по всему массиву данных 

№ биотопа	№ локалитета	Давилко-сутки	N	M–2	M0	M2
1	1	510	85	14479.83	4.00	0.66
1	2	115	11	184.86	4.00	0.37
1	3	160	18	21.90	2.00	0.65
1	4	195	18	335.68	3.00	0.49
1	5	194	33	1098.46	3.00	0.49
1	6	810	130	39922.36	6.00	0.56
1	для биотопа 1	1984	295	66347.85	7.00	0.53
…
9	1	175	9	163.65	3.00	0.63
9	2	175	3	27.00	3.00	0.33
9	3	100	10	110.25	3.00	0.42
9	для биотопа 9	450	22	1501.67	6.00	0.28
0	для всей территории	16126	2043	1455812.8	11.00	0.41

 

Следующий шаг – логарифмирование моментов. В основе фрактального анализа биоразнообразия лежит идея степенной зависимости показателей видового разнообразия от объема природной пробы (объема выборки, площади охваченной территории, продолжительности исследований). Поскольку в логарифмических осях график степенной зависимости становится прямой линией, резонно ожидать, что для сообществ, организованных фрактальным образом, зависимости между логарифмами показателей биоразнообразия и логарифмами показателей масштаба будут линейными (Гелашвили, 2011). Технологически это означает оценку линейности для зависимости между логарифмами моментов для всех выборок lnM_q и логарифмами для их объемов lnN (рис. 3).

 

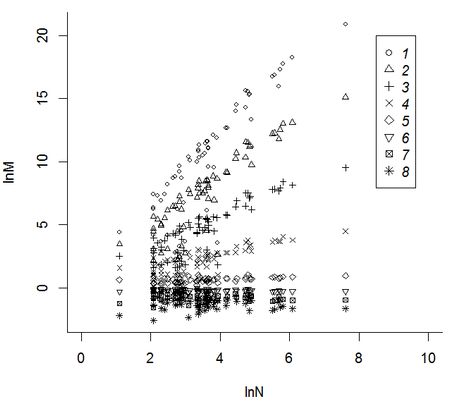
Рис. 3. Зависимость между величинаями lnM_q и lnN: 1-8-значения q в диапазоне от -3 до 3 с шагом 0.75

Fig. 3. The relationship between the values lnM_q and lnN: 1-8 q-values in the range of -3 to 3 in increments of 0.75

 

На первом этапе для этой цели нами был использован дисперсионный анализ Фишера, проверяющий адекватность линейной модели исходным данным (Коросов, 2007). В нашем случае уровень значимости p оказался меньше 0.05 при отрицательных и больше 0.05 при положительных значениях, т. е. линейная модель не адекватна исходным данным (табл. 3, графа p_F). Как известно, это наблюдается, когда зависимость между переменными криволинейна, либо когда высокая изменчивость снижает значимость линейной модели. Рассчитанные для каждого q значения критерия Акаике оказались отрицательными (табл. 3, графа D). Таким образом, доказано, что для отрицательных значений q с ростом масштаба наблюдается криволинейное изменение логарифма моментов. Однако для положительных значений q с ростом масштаба этого сказать нельзя в силу существенной изменчивости данных и отсутствия доказанной зависимости между lnM и lnN.

 

Таблица 3. Уровень значимости линейной модели по критерию Фишера (p_F) и значения критерия Акаике (d)

q	pF	d
-3	< 0.001	-0.59
-2.6	< 0.001	-0.59
-2.2	< 0.001	-0.58
-1.8	< 0.001	-0.57
-1.4	< 0.001	-0.54
-1	< 0.001	-0.48
-0.6	< 0.001	-0.41
-0.2	< 0.001	-0.32
0.2	< 0.001	-0.1
0.6	< 0.001	0.03
1	0.09	0
1.4	0.14	-0.03
1.8	0.18	-0.04
2.2	0.21	-0.05
2.6	0.22	-0.05
3	0.23	-0.05

 

Иными словами, скейлинг структуры сообществ не соответствует степенному закону. В этих случаях есть возможность выполнить локальный мультифрактальный анализ (Якимов и др., 2014), при котором рекомендуется использовать не всю длину масштабной оси, а отрезки для нескольких выборочных масштабов. Автор рекомендации предлагает оценивать углы наклона касательных к сглаженным с помошью сплайна кривым линиям моментов, меняющихя с масштабом. Мы сделали проще, разбив исходную выборку на две группы – в одну объединили пробы для малого и среднего (1 > lnN > 3.8) масштабов (локалитеты и часть биотопов), во вторую – пробы среднего и большого (3.8 > lnN > 7.6) масштабов (часть локалитетов, часть биотопов, общая выборка).

Для каждой из этих выборок продолжили выполнение (теперь уже локального) мультифрактального анализа. Были рассчитаны величины t_q – значения скорости изменения моментов при увеличении размера выборки. Зависимость t_q от q не линейна (рис. 4), т. е. наше сообщество не является монофракталом.

 

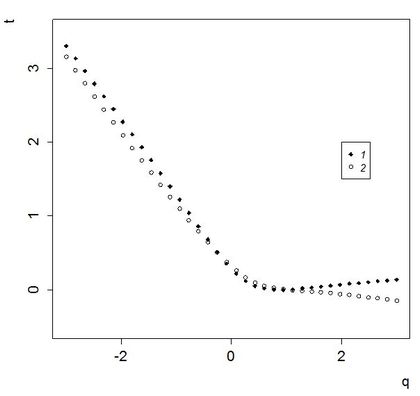
Рис. 4. Динамика t_q: 1– рассчитанная как угол наклона линейной регрессии эмпирического скейлинга моментов, 2 – рассчитанная по последней общей выборке. 

Fig. 4. The dynamics of t_q: 1 – calculated as a tilt angle of the linear regression of empiric scaling of moments; 2 – calculated  on the last total sample.

 

Далее был рассчитан индекс сингулярности a_q, который показывает, меняется ли t_q при изменении q, как именно и в каком диапазоне. Также рассчитывается функция мультифрактального спектра f_a. Если бы сообщество имело монофрактальную структуру, т. е. если бы t_q было линией, то значение a_q было бы единственным, а мультифрактальный спектр свернулся бы в точку с единственным значением f_a, соответствующим мультифрактальной размерности сообщества. Но поскольку функция t_q криволинейна, можно сделать вывод, что мы имеем дело с мультифракталом и поэтому вынуждены рассчитывать и отображать целый спектр значений f_a. Так, для q равного –1.8 индекс сингулярности a_q равен 1, а функция мультифрактального спектра f_a равна 0.13 (табл. 5).

 

Таблица 5. Значения индекса сингулярности и функции мультифрактального спектра 

q	-1.97	-1.8	-0.94	0.09	0.94	1.8	1.97
aq	1.01	1	0.91	0.61	0.08	0.07	0.07
fa	0.11	0.13	0.24	0.31	0.08	0.08	0.09

 

Далее были построены графики мультифрактального спектра – зависимость f_a от а для обеих выборок (рис. 5). Предлагается следующая интерпретация построенных кривых (Гелашвили, 2011). Ордината точек характеризует фрактальную размерность сообщества, абсциссу можно рассматривать как долю видов того или иного подмножества. Левая ветвь спектра характеризует представленность в сообществе доминантных видов, а и правая ветвь – редких видов. Ширина спектра является показателем выравненности видов в сообществе, чем шире спектр, тем меньше выравненность. Высота спектра характеризует видовое разнообразие сообщества, чем выше спектр, тем больше видовое разнообразие.

 

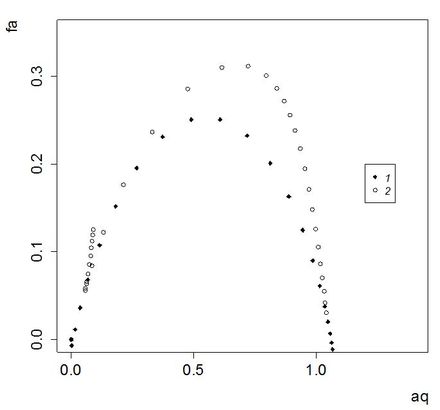
Рис. 5. Кривые мультифрактального спектра для левой (1) и правой (2) частей масштабной шкалы

Fig. 5. Curves of multifractal spectrum to the left (1) and right (2) parts of the scale

 

Как можно видеть на иллюстрации, дуга спектра для малых масштабов существенно ниже дуги для больших масштабов, но обе они примерно одинаковы по ширине. Таким образом и видовое богатство, и доля редких, и доля доминирующих видов выше для выборки больших масштабов. Истоки указанных отличий кроются в составе изученных выборок. Выборки малых и средних масштабов – это результаты непродолжительных учетов в локалитетах и одном из биотопов (болото), мало благоприятном для мелких млекопитающих.  Выборки средних и крупных масштабов – это результаты наиболее продолжительных учетов в локалитетах разных биотопов, а также обобщенные по биотопам выборки и общая выборка. Понятно, что самые продолжительные учеты и объединение учетов по биотопам дают наиболее устойчивую и полноценную картину структуры населения микромаммалий (точные оценки роли разных видов в сообществе). В то же время менее репрезентативные выборки, во-первых, не столь определенно характеризуют роль разных видов (на фоне широкой случайной изменчивости их значимостей), во-вторых, и то не всех.

Обсуждение

 Результаты анализа показали, что для таксоценозов микромаммалий изученных районов фрактальная структура не прослеживается. Такой вывод сделан исходя из доказательства отсутствия линейной зависимости логарифмов моментов от логарифмов меры масштаба в области отрицательных значений q и исходя из отсутствия доказательства линейной зависимости -- для положительных степеней (табл. 3). Важно отметить – анализ диаграммы рассеяния проб не позволяет говорить и о криволинейной связи между этими переменными. Причина отсутствия зависимости очевидна – широкая изменчивость показателей lnM для положительных степеней q (рис. 3, 6).

 

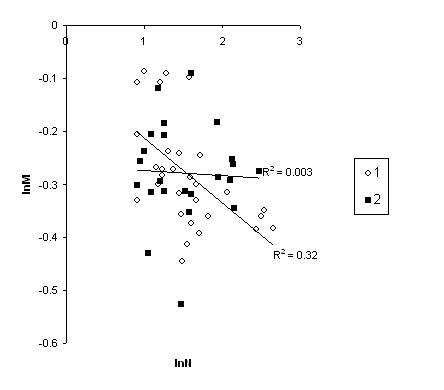
 Рис. 6. Зависимость lnM от lnN при q = 2: 1 – лесные сообщества, 2 – вырубки

 Fig. 6. Dependence of lnM on  lnN at q = 2: 1 – forest communities, 2 – cuttings

 

Причин этого сложного явления может быть несколько. На наш взгляд, фрактальная структура сообществ нарушается из–за антропогенного воздействия. Начиная с 60-х гг. прошлого века на изучаемой территории постоянно велись вырубки леса. Мы выявляем несколько «волн» трансформации (Гусева и др., 2014): масштабные рубки в 60–70-е гг., стагнация в девяностых, активизация рубок с начала века. Вырубки превратили хвойную среднюю тайгу в пеструю мозаику лиственных и хвойно-лиственных фитоценозов, находящихся на разных стадиях сукцессии. Эти мелкоконтурные местообитания населяют более 11 видов мелких млекопитающих в самых причудливых сочетаниях и каждый биотоп и каждая площадка обладает своеобразной структурой сообществ (соотношением значимостей p_i). Вследствие этого моменты для положительных степеней q широко варьируют в области небольших масштабов. Линейность скейлинга моментов ухудшается, правда, не для всех биотопов одинаково. Так, вторичные стации населены в основном доминирующими эврибионтными видами (рыжей полевкой и обыкновенной бурозубкой), поэтому для этих биотопов различие в доле доминирующих видов на малых и средних  масштабах порождает широкую изменчивость моментов (R² = 0.03). Напротив, лесные сообщества с более однообразной и устоявшейся структурой доминирования демонстрируют меньшую изменчивость моментов (R² = 0.32). Анализ обнаружил адекватность линейной зависимости моментов от масштаба для лесных сообществ (p = 0.0009) и ее отсутствие – на разновозрастных вырубках (p = 0.79) (рис. 6).

Вторая очевидная для нас причина отсутствия степенного скейлинга моментов состоит в недостаточной репрезентативности исходных данных. Сопоставим характеристики биоразнообразия двух выборок – для левой и правой частей масштабной шкалы. Как видно на рис. 5, выравненность двух групп примерно одинакова. Казалось бы, увеличение доли доминирующих и редких видов (выявленное  для второй группы) должно сопровождаться снижением выравненности, однако графики спектров показывают, что этого нет – обе группы выборок сходны по этому показателю. Такое возможно, если в группе менее репрезентативных учетов, во-первых, видов меньше, чем в первой группе выборок, и, во-вторых, представленность всех видов широко варьирует без очевидных приоритетов – что и наблюдается для наборов нерегулярных учетов (левой выборки).

Таким образом, анализ полученных диаграмм позволяет выйти на те объемы «промысловых усилий», при которых показатели структуры сообществ мелких млекопитающих должны стабилизироваться. В первом приближении таким числом (порогом репрезентативности) можно принять границу разбиения выборок на две описанные группы – lgN = 3.8, или N = 45. При средней численности зверьков в августе месяце 11 экз./100 д-с (давилко-суток) получается, что на одной пробной площадке необходимо отрабатывать минимум 400 давилко-суток. Учитывая, что для полного цикла динамики сообщества нужно охватить период хотя бы 5 лет, а отдельный учет не должен быть менее 100 д-с, получаем более оправданное число объема отловов на одной площадке – 500 д-с. Примерно такой объем отловов позволяет получить хорошее описание структуры населения на одной площадке отдельного типа биотопа за 5 лет. Если в регионе исследуются 9 типичных местообитаний, изученных хотя бы на 3 площадках в объеме 100 д-с, то для одного сезона получаем 2700 д-с (108 линий по 25 давилок общей длиной 13.5 км); объем отлова должен составить порядка 300 зверьков. Для выполнения такой работы даже в типичный год необходим штат около 10 человек. Таким образом, в рамках наших возможностей (людских, финансовых, территориальных) неточность оценки значимости отдельных видов не может быть ликвидирована. Коль скоро фрактальный анализ требует столь больших выборок, получается, что его очень трудно выполнить в отношении сообществ мелких млекопитающих.

Категоричность этого вывода следует смягчить только тем соображением, что недостижимо большие выборки требуются только для доказательства самоподобия в организации ценозов. Сам же аппарат мультифрактального анализа вполне приложим и к несамоподобным сообществам (например, в форме локального мультифрактального анализа, см. Якимов и др., 2014) как эффективный способ емкого разнопланового описания сложной структуры многих сообществ на обширной территории. Например, сопоставляя мультифрактальные спектры, построенные для выборок, характеризующих разные биотопы, вполе можно получить содержательные заключения (рис. 7).

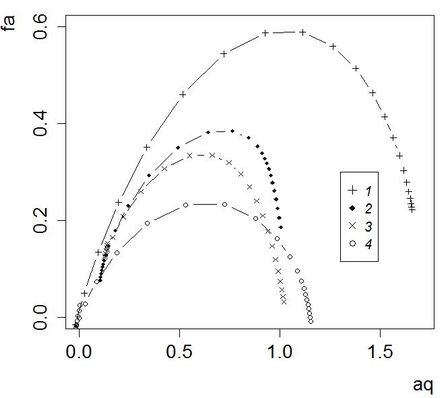
Рис. 7. Мультифрактальные спектры для разных типов биотопов: 1 – молодая вырубка, 2 – лиственный лес, 3 – хвойный лес, 4 – луг

Fig. 7. Multifractal spectra for the different types of habitats: 1 - young cutting, 2 - deciduous forest, 3 - coniferous forest, 4 - meadow

Молодые вырубки отличаются сочетанием частично сохранившегося напочвенного покрова хвойных лесов с развитым разнотравьем, что в летний период привлекает практически все виды микромаммалий региона. По этой причине смешанное видовое богатство в этих биотопах – самое высокое (рис. 7; 1), но выравненность слабая из-за яркого преобладания фоновых эвритопных доминантов (обыкновенной бурозубки и рыжей полевки). На этом фоне луга с неразвитой подстилкой населены только темной полевкой и нечасто посещаются фоновыми доминирующими видами; соответственно, видовое богатство здесь самое низкое, а выравненность невысокая (рис. 7; 4).  Лесные местообитания (рис. 7; 2, 3) обладают более стабильной и сходной структурой доминирования с невысоким биоразнообразием, однако в лиственных лесах (с той или иной примесью хвойных пород) встречается больше видов и с большей численностью, чем в сосняках-зеленомошниках.

Заключение

Что же новое привносит проведенный анализ в наше понимание организации териоценоза микромаммалий? В первую очередь нужно отметить, что для подготовки окончательного варианта представления материалов были выполнены сотни промежуточных вариантов с варьированием структуры изучаемых выборок и методов их объединения. Это позволило существенно лучше оценить достоинства и недостатки накопленных данных, обозначить явные пробелы в потоках биологической информации. Это важный позитивный эффект нашей работы. Выполненный анализ позволил оценить репрезентативность показателей структуры населения мелких млекопитающих. Полученные результаты, на наш взгляд, показывают, что для репрезентативного описания структуры сообщества нужны очень большие наборы данных. Если выборки с одной площадки не должны содержать менее 45 экз. зверьков, то это значит, что многие сезонные и экспедиционные отборы проб не могут сообщить о структуре изучаемых сообществ ничего существенного. Это пессимистическое впечатление, видимо, необходимо проверить методами численного моделирования. Еще одно существенное соображение состоит в том, что для изучаемого района обнаружено явное нарушение степенного скейлинга моментов, нарушение самоподобия населения мелких млекопитающих. В качестве рабочей гипотезы можно принять, что в этом повинна антропогенная мозаичность местообитаний. Однако в предварительной публикации мы решили не углубляться в данную тему. По результатам работы можно сделать ряд конкретных выводов.

1. По данным многолетних учетов в окрестностях с. М. Гомсельга было обнаружено 13 видов мелких млекопитающих ( в августе – 11). 
2. Сообщество мелких млекопитающих окрестностей села М. Гомсельга нельзя назвать самоподобным, поскольку скейлинг логарифмов моментов не удается описать линейной функцией.
3. В список причин отсутствия самоподобия токсоценозов микромаммалий, видимо, следует включить пеструю мозаичность местообитаний, возникших в результате вмешательства человека в форме рубок, а также невысокую и неравную репрезентативность учетов животных на пробных площадках.
4. Процедура мультифрактального анализа сложна, требует больших объемов исходной экологической информации и не обладает  очевидной техникой интерпретации результатов расчетов.
5. Мультифрактальный анализ полезен тем, что позволяет глубоко понять структуру имеющихся материалов и сформировать гораздо более полноценное впечатление о видовой структуре изучаемых сообществ.

Библиография

Благодарности

Авторы выражают признательность С. В. Бугмырину, Л. А. Беспятовой, В. С, Аникановой за участие в сборе материала и В. Н. Якимову за ценные замечания по содержанию статьи.