Введение
Экологическое мировоззрение все ближе к практике: вслед за пониманием всеобщей взаимосвязи явлений в биосфере и зависимости от нее человека от экологии берут стратегию устойчивого развития (принцип существования экосистем). Тактикой новой деятельности становится неистощительное природопользование (там, где это возможно, например в лесном хозяйстве). Все чаще практики природопользования заимствуют у экологии и ее эффективные методы описания динамических систем, в том числе количественные. В нашем сообщении рассмотрен подход к организации неистощительного лесопользования с помощью имитационного моделирования лесной динамики.
В действующем законодательстве РФ большое внимание уделяется определению допускаемых объемов заготовки древесины – «расчетной лесосеки». Приказом Рослесхоза от 27.05.2011 г. № 191 утвержден «Порядок исчисления расчетной лесосеки» с целью определения допустимого ежегодного объема изъятия древесины в эксплуатационных и защитных лесах. Статья 29 Лесного кодекса РФ прямо запрещает заготовку древесины в объеме, превышающем расчетную лесосеку. Таким образом, по закону заготовка древесины в объемах, ведущих к истощению лесов, запрещается. При этом утверждается, что расчетная лесосека определяет ежегодный объем изъятия древесины в эксплуатационных и защитных лесах, обеспечивающий многоцелевое, рациональное, непрерывное, неистощительное использование лесов, исходя из установленных возрастов рубок, сохранения биологического разнообразия, водоохранных, защитных и других полезных свойств лесов.
Однако, по мнению ряда отечественных экспертов (Болотова, 2002; Загадки…, 2014; Отчет…, 2014; Что такое…, 2014; Ярошенко, 2014), существующие методики и подходы к определению расчетной лесосеки, практически не менявшиеся на протяжении XX века, не обеспечивают реальной неистощительности лесопользования по причине наличия существенных недостатков. Это значит, что для России в целом и Республики Карелия в частности актуальным является выработка новых подходов к определению допускаемых объемов заготовки древесины, обеспечивающих реальную неистощительность лесопользования, с учетом установленных возрастов рубок, закономерностей строения и развития древостоев и данных о потребности в древесине.
Цель нашего сообщения состоит в описании нового количественного подхода к определению расчетной лесосеки на базе имитационной модели.
Материалы
При разработке и тестировании имитационной модели были использованы открытые данные лесохозяйственных регламентов центральных лесничеств Республики Карелия (Лесохозяйственные…, 2014) и общие таблицы хода роста нормальных древостоев из справочника «Общесоюзные нормативы для таксации лесов» (Общесоюзные…, 2014).
Традиционные методы исследований
К концу XX века лесной наукой было разработано множество формальных методов для определения объемов расчетных лесосек – например, в работах Н. Н. Свалова, В. В. Антанайтиса и В. В. Загреева (Свалов, 1979; Антанайтис и др., 1981) описывается более 40 различных методов исчисления. Активные исследования в указанном направлении продолжаются до сих пор (см., например, работы (Болотова, 2005; Владимиров и др., 2014 и др.)).
В ряде работ (Свалов, 1979; Болотова, 2004 и др.) отмечается, что среди всех известных методов нет ни одного достаточно универсального. Среди основных причин сложившейся ситуации указанными экспертами выделяются следующие:
- на практике недостаточно учитывается, что объекты регулирования лесопользования (т. е. лесные участки) могут иметь различную исходную возрастную и породную структуру насаждений, например: леса регулированные, относительно равномерно распределенные по возрасту; леса с дефицитом спелых древостоев, леса неурегулированные (природные);
- применяемые на практике методы расчета недостаточно учитывают динамику лесного фонда (т. е. то, что в процессе лесопользования возрастная и породная структура насаждений меняется);
- применяемые на практике методы расчета недостаточно учитывают происходящие процессы лесовосстановления и лесоэксплуатации, вероятные потери от пожаров, нападения лесных вредителей и пр.
Особенно остро недостатки применяемых на практике в России методов расчета объема пользования проявляются при пионерном освоении лесов, когда значительную часть аренды лесопромышленного предприятия занимают ценные малонарушенные лесные территории (Свалов, 1979; Ярошенко, 2014).
Для обеспечения сохранения ценных малонарушенных лесных территорий и постоянства лесопользования (неснижаемости его во времени) необходима выработка новых подходов к исчислению объемов пользования лесом, учитывающих естественную динамику лесов и соблюдающих принцип непрерывности пользования лесом на протяжении всего цикла его развития.
Оригинальные методы исследований
Предваряя наш анализ, выделим защитные и эксплуатационные леса. Задачи сохранения биологического разнообразия, обеспечения водоохранных, защитных и других полезных свойств лесов в условиях лесничеств должны выполняться преимущественно за счет защитных лесов. Вопрос о необходимой площади таких лесов на территории соответствующих лесничеств является весьма актуальным, но выходит за рамки анализа.
Для эксплуатационных лесов в лесничествах должна применяться такая методика оценки расчетной лесосеки, которая гарантирует устойчивое (например, постоянное неснижаемое) обеспечение перерабатывающих предприятий лесного сектора необходимым древесным сырьем на протяжении заранее заданного промежутка времени.
Термин «непрерывное неистощительное лесопользование» в эксплуатационных лесах определяется как возможность использования лесных ресурсов с постоянной высокой эффективностью (при полноценной реализации естественных продуктивных сил леса) на протяжении заранее заданного промежутка времени (или бесконечно). При этом по окончании заданного промежутка времени лес не должен физически исчезнуть на занимаемых площадях, просто его возможности снабжать промышленность древесиной требуемого качества будут полностью исчерпаны. Очевидно, что чем короче планируемый период лесопользования, тем выше уровень использования лесных ресурсов. Такая логика указывает на два ограничения при оценке объемов «расчетной лесосеки». Во-первых, они относятся к заранее заданному периоду лесопользования конечной продолжительности и, во-вторых, они должны обеспечивать постоянство максимально возможного изъятия лесных ресурсов на этот период.
Мы предлагаем подход к определению расчетной лесосеки для эксплуатационных лесов основать на базе имитационной модели динамики возрастной структуры насаждений, учитывающей все возрастные классы – от начальных («молодняки») до старших («спелые леса»).
В отличие от применяемых ныне формул расчета лесосеки, основанных на мысленной модели истощения запасов перестойных, спелых, приспевающих и других насаждений через то или иное время, имитационная модель рассчитывает этот процесс во всех деталях относительно всех разновозрастных групп деревьев. По существу в числовой форме (виртуально, в недрах компьютера) воссоздается и прогнозируется история леса на протяжении любого отрезка времени. Вырубки рассматриваются как скачкообразное и территориально локализованное изменение возрастной структуры древостоя, а модель призвана рассчитать их последствия и дать возможность решать задачи расчета оптимальной величины «расчетной лесосеки» при задаваемых ограничениях на данной территории. Модель позволяет вычислять допускаемые объемы заготовки древесины (расчетной лесосеки) в эксплуатационных лесах с различной исходной возрастной структурой и различной интенсивностью лесопользования.
Моделирование возрастной структуры насаждения
В отдельный момент времени древостой одного возраста занимает площадь ai,j (i – момент времени, j – возраст, a – площадь). В отдельный момент времени i возрастная структура насаждения представлена набором значений относительной площади древостоев разного возраста.
Сумма относительных площадей всех участков разновозрастных древостоев составляет единицу (вся площадь, занимаемая насаждением), т. е.:
∑ ai,j = 1. [1]
В следующий момент времени i + 1 моделируется переход древостоев каждого возрастного класса в более старший ai+1, j+1 = ai,j – древостой на некоем участке на следующем временном шаге переходит в следующий возрастной класс. Шаг возрастной и временной шкалы в модели составляет один год.
В модели учитываются процессы естественного отмирания (sdj), нарушения из-за внешних (включая антропогенные) случайных воздействий (saj), последствия рубок (scj). Они задаются в форме коэффициентов выживания (s – survival; d – death, a – anthropogenic, c – cut). В зависимости от возраста (j) эти коэффициенты могут меняться.
Значения коэффициентов, учитывающих процессы естественного отмирания (sdj) и нарушения из-за внешних случайных воздействий (saj), выбираются по соответствующей специальной литературе и помещаются во встроенных базах данных при программной реализации данной имитационной модели.
Например, для древостоя сосны обыкновенной в возрасте 5 лет вероятность выживания составляет 100 %, sd5 = 1; вероятность нарушения внешними случайными воздействиями составляет 5 % (а сохранения – 95 %; sa5 = 0,95); вероятность быть вырубленным – нулевая (sc5 = 1). Аналогичные цифры для 100 лет: sd100= 1,00; sa100 = 0,95; sс100 = от 0 до 1.
Полная формула перехода древостоев каждого возрастного класса в более старший имеет вид:
ai+1, j+1 = sdj × saj × scj × ai,j. [2]
Значения коэффициентов естественного отмирания (sdj) назначаются при программной реализации математической модели, исходя из данных о продолжительности жизни отдельных деревьев, древостоев в целом и данных о динамике прироста запасов древостоев на корню.
В справочнике (Общесоюзные…, 2014) имеются указания на то, что запас наиболее характерных для европейской части России лесообразующих хвойных пород (сосны и ели) постепенно увеличивается до возраста естественной спелости, затем начинает уменьшаться, в возрасте около 180 лет прирост становится практически нулевым. Известно (Спелость…, 2014), что возраст естественной спелости у деревьев сосны или ели наступает к 300–350 годам, а у их насаждений — к 200–250 годам. Из работ (Арефьев, 2014; Булыгин, 1991) также известно, что береза живет в среднем до 100–120 лет, осина – до 80–100 лет. В модели принято, что предельный возраст хвойных (сосна, ель) насаждений составляет 250 лет, березовых – 130 лет, осиновых – 100 лет.
С учетом изложенного для программной реализации имитационной модели были приняты параметры отмирания наиболее характерных для европейской части России лесообразующих пород деревьев (табл. 1).
Таблица 1. Параметры естественного вымирания основных лесообразующих пород деревьев
| Показатель | Порода | ||
| сосна, ель | береза | осина | |
| Возраст начала вымирания, лет | 180 | 90 | 70 |
| Возраст полного вымирания, лет | 250 | 130 | 100 |
| Уровень ежегодной гибели | 0.05 | 0.08 | 0.11 |
Переводя вышеизложенные факты в используемые в модели единицы площади, приходим к следующим оценкам (для сосны): до возраста насаждений 180 лет естественной убыли площади древостоя не происходит (sd,0-180 = 1); начиная со 180 лет задается прогрессивное снижение площади на 5 % (сохранение – 95 %) sd,180-249 = 0,95. К 249 годам доля перестойных древостоев снизится до 3 % от доли в 180 лет. Для возраста 250 лет принята убыль 100 % – sd,250 = 0.
Значения коэффициентов случайного отмирания (sdj) назначаются при программной реализации имитационной модели, исходя из данных исследований случайной гибели древостоев разного возраста.
По некоторым данным (Forest…, 2013), за период 2004–2008 гг. в Финляндии серьезно пострадало 4.4 % лесных площадей, умеренно пострадало 23.9 %; принимаем оценку: 5 % отмирания (95 % сохранения) – sa,j = 0.95. В то же время проблема определения конкретных значений коэффициента случайного отмирания (sdj) является весьма актуальной (см., например, работы: Болотов и др., 2005; Болотова, 2002) и требует дополнительных исследований.
Определение величины коэффициентов гибели от рубок (scj) и составляет предмет модельного исследования. Они варьируются в модели с целью поиска оптимального варианта лесопользования. Эта технология рассмотрена ниже.
Исходя из формулы перехода древостоев в более старший возрастной класс на каждом i-м шаге, общие потери площадей древостоя составят
(ai,j – sdj × saj × scj × ai,j). [3]
Любые нарушения сплошного растительного покрова (вывалы и ветровалы, пожары и рубки) ведут к появлению территорий без деревьев, которые рассматриваются как пополнение площади (доли) древостоев нулевого возрастного класса (ai,0). Поскольку такие нарушения возможны на территории древостоя любого возраста, нулевой класс в следующий (i + 1) момент времени сформирован суммой площадей с нарушенным древостоем по всем возрастным классам:
ai+1,0 = ∑ (ai,j – sdj × saj × scj × ai,j). [4]
Результатом расчетов по модели является таблица из значений ai,j размером m × k, где m – число шагов модели (продолжительность периода времени для прогноза); k – число возрастных классов. Набор этих значений можно анализировать, представлять в виде диаграмм и пр., а также использовать при настройке параметров функционирования при оценке возможностей неистощительного лесопользования.
Моделирование рубок насаждений
Вырубки представляют собой изъятие деревьев старших возрастных классов (в примере – старше 80 лет, т. е. j > 80) и переход этих площадей в категорию нулевого возрастного класса. Однако вырубаться может только лес на корню, из площади которого уже вычли потери от действия внутренних и внешних факторов (sdj × saj × ai,j):
сi+1, j>80 = ∑ (sdj × saj × ai,j – sdj × saj × scj × ai,j). [5]
Зная запас древесины на 1 га для каждого возрастного класса (Rj), несложно рассчитать объемы рубки древесины (v i+1) на каждом временном шаге модели:
v i+1 = ∑ (Rj × сi+1, j>80). [6]
Запас древесины на 1 га для древостоев всех классов возраста при программной реализации модели определяется по количественным моделям хода роста соответствующих насаждений, построенным на основе общих таблиц хода роста нормальных древостоев (Общесоюзные…, 2014). Вместо таблиц (Общесоюзные…, 2014) могут использоваться таблицы, составленные научным коллективом под руководством профессора А. З. Швиденко (Швиденко и др., 2008), или другие аналогичные.
Поскольку в лесохозяйственных регламентах центральных лесничеств для хвойных пород используются две категории продуктивности: 1–3 и 4–5 классы бонитетов, а для лиственных – одна категория продуктивности, то для построения математических моделей хода роста значения из первоисточника (Общесоюзные…, 2014) усреднялись (см. пример в табл. 2).
К сожалению, указанные материалы (табл. 2) недостаточны для непосредственного моделирования хода роста соответствующих древостоев по двум причинам. Во-первых, они не дают представления о запасе в древостоях старше 160 лет, во-вторых, запас так называемого нормального древостоя существенно выше запаса реальных древостоев.
Например, для сосны 4–5-го классов бонитета нормальный запас в возрасте 100 лет составляет 186 кбм/га (табл. 2), а по лесохозяйственному регламенту Медвежьегорского центрального лесничества Республики Карелия (Лесохозяйственные…, 2014) для спелых и перестойных сосновых насаждений 4–5-го бонитета в эксплуатационных лесах – 154 кбм/га.
Таблица 2. Запасы стволовой древесины в нормальных древостоях, кбм/га
| Возраст, лет | Сосна | Ель | Береза | Осина | ||
| 1–3 бон. | 4–5а бон. | 1–3 бон. | 4–5а бон. | 1–5 бон. | 1–5 бон. | |
| 10 | 28 | 19 | – | 18 | 34 | |
| 20 | 79 | 25 | 64 | – | 51 | 82 |
| 30 | 137 | 44 | 135 | 21 | 88 | 132 |
| 40 | 202 | 68 | 226 | 36 | 123 | 177 |
| 50 | 266 | 92 | 326 | 56 | 155 | 218 |
| 60 | 320 | 116 | 426 | 79 | 182 | 252 |
| 70 | 367 | 137 | 521 | 103 | 204 | 280 |
| 80 | 405 | 156 | 604 | 128 | 222 | 302 |
| 90 | 439 | 172 | 675 | 152 | 237 | 320 |
| 100 | 466 | 186 | 735 | 175 | 249 | 335 |
| 110 | 486 | 197 | 783 | 195 | – | – |
| 120 | 504 | 206 | 820 | 211 | – | – |
| 130 | 520 | 215 | 852 | 225 | – | – |
| 140 | 534 | 223 | 878 | 238 | – | – |
| 150 | 547 | 230 | 901 | 249 | – | – |
| 160 | 558 | 236 | 921 | 259 | – | – |
По этим причинам данные из таблиц хода роста нормальных древостоев (Общесоюзные…, 2014) были преобразованы следующим образом.
Сначала по имеющимся исходным данным (табл. 2) были рассчитаны кривые изменения запасов древесины с возрастом; использованы уравнения полиномов 2-й степени вида:
Rн= a0 + a1 × i + a2 × i 2, [7]
где а – коэффициенты полинома (табл. 3), i – возраст древостоя.
Таблица 3. Коэффициенты для кривых изменения запасов в нормальных древостоях
| Коэффициент | Сосна | Ель | Береза | Осина | ||
| 1–3 бон. | 4–5а бон. | 1–3 бон. | 4–5а бон. | 1–5 бон. | 1–5 бон. | |
| a0 | –56.4111 | –16.5509 | –120.995 | –12.9605 | –27.9833 | –29.55 |
| a1 | 7.589699 | 2.584391 | 8.631785 | 2.520494 | 6.153719 | 4.539637 |
| a2 | –0.02381 | –0.00616 | –0.02038 | –0.00589 | –0.02527 | –0.01746 |
Полученные кривые изменения запаса позволили, в частности, рассчитать возможный запас нормального древостоя для возрастных групп старше 160 лет. Уравнения получены: для сосны и ели двух групп бонитетов (1–3 и 4–5а), для осины и березы всех классов бонитета; всего 6 уравнений.
Затем был введен поправочный коэффициент (K) для расчета кривых изменения запасов древостоя с возрастом для условий каждого конкретного лесничества (Rл), исходя из простого соображения, что эта величина будет отличаться от запаса нормального древостоя (Rн) на величину K:
K = Rл / Rн. [8]
Поправочный коэффициент вычисляется, исходя из соотношения величины запаса древостоя, приведенной в лесохозяйственном регламенте для конкретного района, и величины запаса, рассчитанной по модели динамики запаса нормального древостоя.
Например, для насаждений сосны 4–5-го бонитета Медвежьегорского центрального лесничества Республики Карелия (Лесохозяйственные…, 2014) в возрасте 100 лет модель дает «нормальный» запас, равный
Rн100 = –16.5509 + 2.584391 × 100 – 0.00616 × 1002 = 180.3 кбм/га,
а в лесохозяйственном регламенте указана величина 154 кбм/га, следовательно, искомый коэффициент равен
K = Rл100 / Rн100 = 154 /180.3 = 0.854248.
В дальнейшем этот и другие коэффициенты (табл. 4) используются для определения запасов сосновых древостоев 4–5-го бонитета эксплуатационных лесов Медвежьегорского центрального лесничества Республики Карелия (Лесохозяйственные…, 2014) любого возраста i по формуле:
Rлi = K × Rнi. [9]
Таблица 4. Поправочные коэффициенты для Медвежьегорского центрального лесничества
| Коэффициент | Сосна | Ель | Береза | Осина | ||
| 1–3 бон. | 4–5а бон. | 1–3 бон. | 4–5а бон. | 1–5 бон. | 1–5 бон. | |
| K | 0.637542 | 0.854248 | 0.585236 | 0.960368 | 0.82142 | 0.922408 |
Аналогичным образом вычисляются поправочные коэффициенты для условий каждого конкретного лесничества. При программной реализации математической модели разработан соответствующий блок программы, рассчитывающий эти коэффициенты. От пользователя требуется ввести значения запаса на 1 га для спелых и перестойных древостоев, приведенного в лесохозяйственном регламенте данного региона, программа сравнивает введенное значение с табличными и рассчитывает необходимый поправочный коэффициент для всех возрастных групп.
Оценка «расчетной лесосеки» неистощительного пользования
При вычислении параметров «расчетной лесосеки», обеспечивающей непрерывное неистощительное лесопользование в эксплуатационных лесах, возможно рассматривать два варианта.
Вариант I. «Непрерывное неистощительное лесопользование» в эксплуатационных лесах можно понимать как ежегодное изъятие максимально возможного объема древесины на протяжении заданного числа лет путем ежегодной вырубки территории одного и того же размера (т. е. постоянство рубок по площади (Синицын и др., 1973)).
Этим постулируется, что площадь рубок на протяжении всего периода прогноза должна быть постоянной и максимально возможной; например, для спелых древостоев:
сi, j>80 = const –> max. [10]
При этом в зависимости от запасов разновозрастной древесины и закономерного изменения возрастного состава общий вырубаемый объем древесины (v) будет год от года варьировать.
Вариант II. «Непрерывное неистощительное лесопользование» в эксплуатационных лесах можно понимать как изъятие максимально возможного и постоянного объема древесины на протяжении заданного числа лет путем ежегодной вырубки территории различных размеров (т. е. постоянство рубок по объему древесины (Синицын и др., 1973)).
Этим постулируется, что площадь рубки на протяжении периода прогноза может варьировать, но общий вырубаемый объем древесины должен быть постоянным и максимально большим:
vi = const –> max. [11]
В зависимости от запасов разновозрастной древесины и закономерного изменения возрастного состава год от года варьировать будет уже площадь рубок. Электронные компьютерные средства позволяют рассчитать не один, но множество сценариев, при которых объемы рубок могут варьировать. Каждый из сценариев будет иметь свой критерий реализации. Если критерий количественно определен, он вводится в процедуру оптимизации, которая подбирает такие параметры модели (объемы и/или площади рубок), чтобы заданный критерий был выполнен.
При этом могут быть решены три основных задачи.
1. Вычислить продолжительность периода времени, в течение которого можно постоянно изымать произвольно заданный объем древесины требуемого возраста (в гектарах площади необходимых вырубок или в кубометрах необходимого объема заготовок); эта задача не ограничена никакими критериями и выполняется как простой расчет динамики древостоя при рубках той или иной интенсивности. Расчет останавливается, когда запасы древесины требуемого возраста будут полностью истощены; это и будет возможная продолжительность рубок. Обычная динамика возрастной структуры насаждения сводится к тому, что если принять завышенную расчетную лесосеку, вычисленную по известным формулам (Приказ…, 2014), то ресурсы спелых и перестойных древостоев заканчиваются через 35–50 лет (рис. 1).
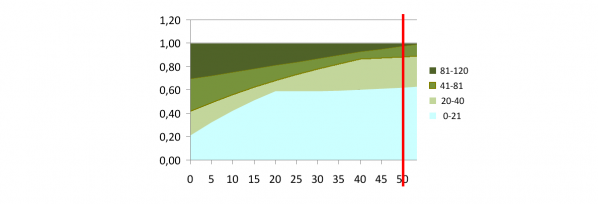
Рис. 1. Изменение соотношения площадей четырех возрастных групп насаждения при использовании завышенных размеров расчетной лесосеки. По оси ординат – доля площади данной группы от всей площади изучаемого района. По оси абсцисс – годы жизни древостоя. Красной чертой отмечена дата, после которой расчетная лесосека становится не обеспеченной лесными ресурсами
Fig. 1. Changes in the ratio of the areas of four age groups of the stand when using oversized allowable cut. The ordinate – part of the studied area occupied by a certain age group. The abscissa – years of life of the stand. Red line denotes the date after which the allowable cut is not provided by forest resources
2. Вычислить максимально возможную ежегодную площадь расчетной лесосеки, которая будет постоянно доступна для рубки в течение произвольно заданного периода времени. Обычная динамика возрастной структуры насаждения демонстрирует плавное снижение площади древостоев (например, спелых и перестойных), назначенных в рубку, вплоть до полного их сведения в последний год прогнозируемого периода (рис. 2).
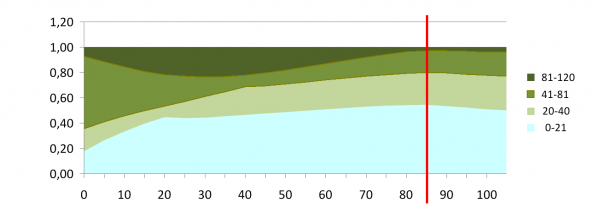
Рис. 2. Изменение соотношения площадей четырех возрастных групп насаждения при условии постоянства площади расчетной лесосеки «главного пользования» на 100 лет. По оси ординат – доля площади данной группы от всей площади изучаемого района. По оси абсцисс – годы жизни древостоя. Красной чертой отмечена дата, после которой расчетная лесосека становится не обеспеченной лесными ресурсами
Fig. 2. Changes in the ratio of the areas of four age groups of the stand provided that the area of the allowable cut of «principal use» is constant for 100 years. The ordinate – part of the studied area occupied by the certain age group. The abscissa – years of life of the stand. Red line denotes the date after which allowable cut is not provided by forest resources
3. Вычислить площадь расчетной лесосеки, вырубка которой будет обеспечивать ежегодно максимально возможный и постоянный объем древесины в течение произвольно заданного периода времени (без варьирований объемов и перерывов в лесодобыче в указанный период). Обычная динамика выглядит вначале как постепенное возрастание площадей рубок (по мере вырубания более продуктивных старших возрастных групп и замене их менее продуктивными младшими) и последующая стабилизация площадей рубок, когда старшие древостои будут в основном сведены (рис. 3, 4).
Отличие от предыдущего варианта состоит в том, что при изменении возрастного состава и, следовательно, запасов на корню для обеспечения заготовок заданного объема древесины в разные годы потребуется вырубать разные площади.
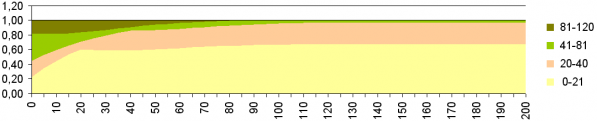
Рис. 3. Изменение соотношения площадей четырех возрастных групп насаждения при условии понижения возраста рубки и постоянства объемов заготовки древесины на 200 лет. По оси ординат – доля площади данной группы от всей площади изучаемого района. По оси абсцисс – годы жизни древостоя
Fig. 3. Changes in the ratio of the areas of four age groups of the stand under the condition of reduced cutting age and constant harvesting volumes for 200 years. The ordinate – part of the studied area occupied by a certain age group . Abscissa – years of life of the stand.
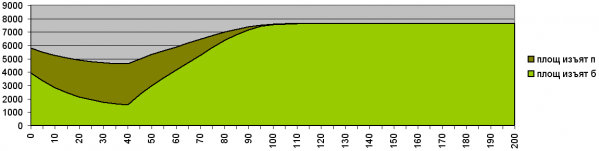
Рис. 4. Изменение соотношения площадей рубок «старших», «п» (спелых), и «младших», «б», возрастных групп в насаждении при условии понижения возраста рубки и постоянства объемов заготовки древесины на 200 лет. По оси ординат – доля площади данной группы от всей площади изучаемого района. По оси абсцисс – годы жизни древостоя
Fig. 4. Changes in the ratio of the cutting areas of «senior», «п» (mature) and «junior», «б» age groups of the stand under the condition of reduced cutting age and constant harvesting volumes for 200 years. The ordinate – part of the studied area occupied by a certain age group. The abscissa – years of life of the stand.
Программная реализация разработанных моделей осуществлялась в двух программных средах.
Среда Excel
Построение модели возрастной структуры насаждения и проверку ее работоспособности проводили в среде пакета MS Excel. За основу была взята технология табличного программирования, при котором на листе Excel строится имитационная система, открывающая возможность настройки модельных параметров встроенными методами оптимизации пакета (Коросов, 2002).
При этой технологии сама модель (матрица возрастной структуры) строится на листе Excel как набор множества стереотипных формул, вычисляющих переход одновозрастной группы во все более старшие возрастные классы с учетом потерь от различных факторов (отмирания, нарушения, рубки).
Модель настраивалась с помощью встроенного макроса процедуры оптимизации «Поиск решения». В такой форме модель имеет прозрачную структуру и средства иллюстрации и доступна для предметного обсуждения специалистами разных профилей (рис. 5).
Помимо отмеченных преимуществ, наглядности и прозрачности, модель, реализованная в среде Excel, обладает отрицательным качеством – крайней громоздкостью; в таком виде она не годится для программирования на алгоритмических языках.
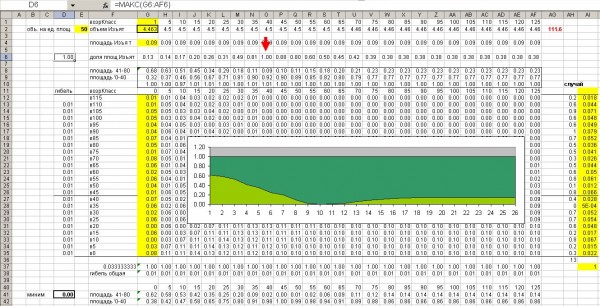
Рис. 5. Общий вид имитационной модели в среде Excel
Fig. 5. General view of the simulation model in Excel
Среда JavaScript
Для практической апробации и широкого обсуждения предлагаемого авторами подхода и моделей была разработана компьютерная программа на языке JavaScript (JavaScript…, 2014). Программная реализация модели на языке JavaScript в целом копирует структуру модели, созданной в среде Excel. При отладке программы на JavaScript использовались результаты моделирования в среде Excel.
Достоинством JavaScript является возможность создания общедоступной через сеть Интернет программы с удобным для пользователей интерфейсом ввода-вывода данных. Программа на JavaScript может работать на компьютере с любой операционной системой, в среде web-браузера, в котором включена обработка javascript-сценариев (по умолчанию она включена).
Разработанная программа на JavaScript (рис. 6) размещена в тестовом режиме в сети Интернет по адресу: http://hcvf.ru/lesoseka/ (вкладка «Новый метод расчета лесосеки») и может быть перенесена на другой адрес. Здесь же размещена краткая справка по самой программе. Программа работает во всех современных web-браузерах (Firefox, Opera, Chrome, Safari, Yandex, Internet Explorer).
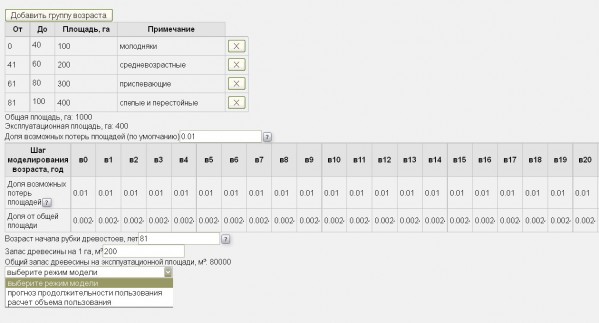
Рис. 6. Фрагмент интерфейса программы для исчисления объема пользования лесом на основе предлагаемого подхода
Fig. 6. Fragment of the interface for the calculation of the volume of forest utilization on the basis of the proposed approach
Разработанная на языке JavaScript программа предназначена для вычисления параметров расчетной лесосеки в спелых и перестойных лесах, обеспечивающей непрерывное неистощительное лесопользование в эксплуатационных лесах. При вычислении используются открытые исходные данные из лесохозяйственных регламентов центральных лесничеств и лесных планов субъектов РФ: площади древостоев различных классов возраста, запас на 1 га в спелых и перестойных древостоях, возраст рубки спелых и перестойных насаждений.
Математическое моделирование хода роста и изменения запаса соответствующих насаждений (см. формулы [6–9]) здесь не применяется, в соответствии с предназначением программы.
Программа позволяет моделировать изменения соотношения площадей возрастных групп насаждения монопородного состава и вычислять на этой основе объемы или площади изъятия лесных ресурсов (параметры расчетной лесосеки) при сплошных рубках, обеспечивающие непрерывное неистощительное лесопользование в спелых эксплуатационных лесах на протяжении всего периода прогноза. Программа обеспечивает моделирование результатов постепенных и выборочных рубок в спелых эксплуатационных лесах.
Для моделирования постепенных (выборочных) рубок исчисление требуемой площади расчетной лесосеки производится путем деления общего запаса древесины, намеченного к изъятию при рубках в соответствующем насаждении, на соответствующий средний запас древесины на гектаре в спелых и перестойных древостоях. Если известна только площадь постепенных (выборочных) рубок, то вычисление общего запаса, намеченного к изъятию, производится путем умножения этой площади на средний запас древесины на гектаре с учетом среднего процента выборки от общего запаса (также приводится в лесохозяйственных регламентах).
Программа может работать в двух режимах:
- «прогноз продолжительности пользования» – прогноз продолжительности пользования спелыми и перестойными древостоями при заранее известном ежегодном объеме их рубки. При выборе этого режима необходимо дополнительно задать планируемый ежегодный объем рубки леса и продолжительность периода прогноза;
- «расчет объема пользования» – расчет объема равномерного пользования спелыми и перестойными древостоями на период прогноза. При выборе этого режима необходимо дополнительно задать продолжительность периода прогноза (желаемое количество лет пользования).
Результаты расчетов в режиме «прогноз продолжительности пользования» выводятся в виде таблицы и графика динамики долей от общей площади всех возрастных групп. Продолжительность пользования лесом при заранее известном ежегодном объеме их рубки указывается на графике.
Результаты расчетов в режиме «расчет объема пользования» выводятся в виде таблицы и графика динамики долей от общей площади всех возрастных групп. Также указывается ежегодный расчетный объем равномерного пользования лесом (т. е. рубки леса) на период прогноза.
Обсуждение
Согласно лесохозяйственному регламенту Пудожского центрального лесничества Республики Карелия (Лесохозяйственные регламенты…, 2014), площадь сосняков 1–3-го классов бонитета составляет 54575 га, в т. ч.: молодняки – 14752 га; средневозрастные – 6559 га; приспевающие – 12435 га; спелые и перестойные насаждения – 20829 га. Средний запас на 1 га в спелых и перестойных насаждениях – 276 куб. м. Рекомендуемая расчетная лесосека – «интегральная», 618 га/год.
Расчет на период 100 лет с помощью разработанной программы показал следующее:
– ежегодная заготовка в объеме 170 тыс. куб. м древесины («интегральная» расчетная лесосека, 618 га/год) возможна на прогнозируемый период. Изменение соотношения групп возраста представлено на рис. 7;
– максимально возможный ежегодный объем заготовки древесины на прогнозируемый период составляет 183 тыс. куб. м (т. е. примерно 666 га/год). При этом важно понимать, что к концу прогнозируемого периода спелые и перестойные насаждения будут полностью вырублены (рис. 8).
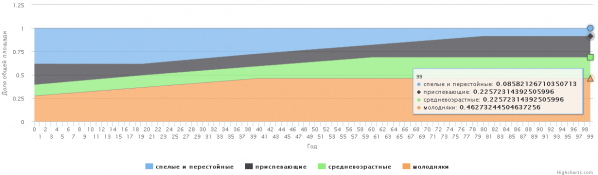
Рис. 7. Динамика соотношения древостоев различных групп возраста при ежегодной заготовке 170 тыс. куб. м древесины (618 га/год) в сосняках 1–3-го бонитета Пудожского центрального лесничества Карелии (отображение результатов расчетов по программе в окне браузера)
Fig. 7. Dynamics of the ratio of different age group stands when harvesting annually 170 thousand cu. meters of timber (618 ha / year) in pine forests of 1–3 yield class in Pudozhsky central forestry of Karelia (the results of computing using the program are displayed in browser)
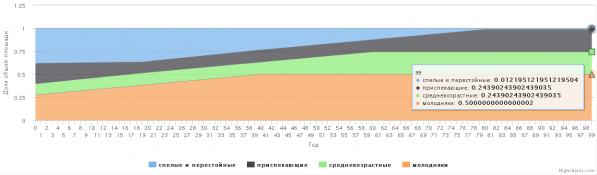
Рис. 8. Динамика соотношения древостоев различных групп возраста при ежегодной заготовке 183 тыс. куб. м древесины (666 га/год) в сосняках 1–3-го бонитета Пудожского центрального лесничества Карелии (отображение результатов расчетов по программе в окне браузера)
Fig. 8. Dynamics of the ratio of different age group stands when harvesting annually 183 thousand cu. meters of timber (666 ha / year) in pine forests of 1–3 yield class in Pudozhsky central forestry of Karelia (the results of computing using the program are displayed in browser)
Таким образом, для рассмотренного примера рекомендуемая по лесохозяйственному регламенту «интегральная» расчетная лесосека в размере 618 га/год может считаться приемлемой на весь период прогноза (100 лет). Если ставить задачу максимально использовать (т. е. полностью вырубить) спелые и перестойные сосняки в течение 100 лет, то ежегодный объем пользования можно увеличить до 183 тыс. куб. м (666 га/год).
Заметим, что данная рекомендация в целом соответствует цифрам так называемой лесосеки равномерного пользования (674 га/год) и второй возрастной лесосеки (664 га/год), указанных в лесохозяйственном регламенте Пудожского центрального лесничества Республики Карелия (Лесохозяйственные…, 2014).
Аналогичные вычисления легко могут быть выполнены заинтересованными экспертами с помощью разработанной программы, на основе открытых исходных данных из лесохозяйственных регламентов центральных лесничеств и лесных планов субъектов РФ.
Заключение или выводы
Авторами предлагается новый подход к определению расчетной лесосеки для спелых и перестойных эксплуатационных лесов и разработанные на его основе компьютерные программы, которые позволяют вычислять параметры расчетной лесосеки, обеспечивающей непрерывное неистощительное лесопользование в этих лесах, на протяжении заданного числа лет.
В отличие от применяемых ныне формул для исчисления расчетной лесосеки, основанных на мысленной модели истощения запасов перестойных, спелых, приспевающих и других насаждений через то или иное время, с помощью предлагаемого подхода можно количественно воспроизвести этот процесс во всех деталях относительно всех разновозрастных групп деревьев. Модельное представление обеспечивает значительно бóльшую универсальность, чем формальное, поскольку, во-первых, позволяет рассчитывать любые характеристики изучаемого процесса, а не только те, что позволяют применяемые формулы, во-вторых, параметры модели могут быть с помощью специальных процедур подстроены под реальные данные, что позволит давать гораздо более реалистичные прогнозы результатов лесопользования.
Опыт разработки предлагаемого подхода и программ на его основе подсказывает следующие основные направления дальнейших исследований:
1. Следует детализировать уже разработанные модели и программы:
а) учесть в модели все типы рубок – сплошные, постепенные, выборочные и рубки ухода, а также связанные с ними эффекты изменения продуктивности, породного состава и запаса насаждения (сейчас учитываются только рубки сплошные, менее точно – постепенные и выборочные);
б) увеличить перечень пород деревьев (и соответствующих им баз данных с характеристиками), для которых может быть выполнена оценка расчетной лесосеки (сейчас охвачено 4 породы);
в) учесть в модели эффекты «накопления» запасов спелых и перестойных насаждений при эксплуатации насаждений, ранее истощенных рубками (т. е. имеющих на начальном этапе моделирования дефицит спелых и приспевающих древостоев, при избытке молодняков).
2. Выйти на моделирование территориального аспекта лесозаготовок:
а) с использованием ГИС-технологий построить модель пространственно-временной динамики насаждений для целей распределения площадей рубок по территории, проектирования сети дорог и других необходимых лесохозяйственных мероприятий;
б) с использованием ГИС-технологий построить модель распределения площадей рубок по территории с учетом транспортной и экономической доступности лесов, а также других природных и производственных факторов (в настоящее время пространственный фактор не учитывается);
в) создать программу автоматического проектирования (оптимизации) сети лесных дорог на основе прогнозируемых объемов (площадей) изъятия лесных ресурсов в долгосрочной перспективе (результаты подобных разработок уже опубликованы – (Болотов и др., 2005; Владимирови др., 2014 и др.)).
В заключение следует отметить, что проблема расчета неистощительного объема пользования лесом имеет особое значение для лесных предприятий, сертифицированных или сертифицируемых по системе FSC (поскольку наличие сертификата FSC подразумевает соблюдение предприятием не только норм и требований действующего законодательства, но и принципов, критериев и требований национального стандарта FSC).
Предлагаемый новый подход рекомендуется для апробации в условиях указанных предприятий. При этом важно учесть, что в связи с внедрением лесной сертификации не все эксплуатационные леса могут использоваться в полном объеме. В эксплуатационных лесах таких предприятий возможно исключение из расчета лесопользования так называемых лесов высокой природоохранной ценности, репрезентативных участков лесных экосистем, не исключенных из расчета лесопользования законодательно.
По результатам апробации возможны дальнейшие усовершенствования предлагаемого подхода, а также выпуск инструкций и рекомендаций, облегчающих практическую работу по вычислению необходимых показателей.
Библиография
Антанайтис В. В., Загреев В. В. Прирост леса . М.: Лесн. пром-сть, 1981. 200 с.
Арефьев С. П. О максимальном возрасте деревьев на территории Тюменской области // Путь в Сибирь. URL: http://library.ikz.ru/georg-steller/aus-sibirien-2013-2009/arefev-s.-p.-o-maksimalnom-vozraste-derevev-na (дата обращения: 13.05.2014).
Болотов О. В., Ельдештейн Ю. М., Болотова А. С. и др. Основы расчета и планирования устойчивого управления лесами и лесопользованием: монография . Красноярск: СибГТУ, 2005. 181 с.
Болотова А. С. Определение расчетной лесосеки на основе моделирования динамики лесного фонда: Автореф. дисс. … канд. с.-х. наук. Красноярск, 2002. 24 с. // disserCat – электронная библиотека диссертаций. URL: http://www.dissercat.com/content/opredelenie-raschetnoi-lesoseki-na-osnove-modelirovaniya-dinamiki-lesnogo-fonda (дата обращения: 22.07.2014).
Болотова А. С. К методике определения расчетной лесосеки // Web-сайт Брянской государственной инженерно-технологической академии (БГИТА). URL: http://science-bsea.bgita.ru/2004/les_2004/bolotova_metodika.htm (дата обращения: 22.07.2014).
Булыгин Н. Е. Дендрология: учебник для высш. учеб. заведений . Л.: Агропромиздат, Ленингр. отд-ние, 1991. 352 с.
Владимиров И. Н., Попова А. К. Моделирование пространственно-временной динамики лесных ресурсов с использованием интеллектной ГИС // Академическое издательство «ГЕО». URL: http://www.izdatgeo.ru/pdf/gipr/2009-1/26.pdf (дата обращения: 22.07.2014).
Загадки расчетной лесосеки: рубим мало? // Forest.ru – Все о российских лесах. URL: http://old.forest.ru/rus/problems/myths/lesoseka.html (дата обращения: 22.07.2014).
Коросов А. В. Имитационное моделирование в среде MS Excel (на примерах из экологии) . Петрозаводск: Изд-во ПетрГУ, 2002. 212 с.
Лесохозяйственные регламенты центральных лесничеств Карелии на 2012–2021 гг. // Официальный интернет-портал Республики Карелия «Карелия официальная». URL: http://gov.karelia.ru/gov/Power/Committee/Forest/lh_regl21.html (дата обращения: 13.05.2014).
Общесоюзные нормативы для таксации лесов (утв. Приказом Госкомлеса СССР от 28.02.1989 г. № 38) // Консультант Плюс. URL: http://base.consultant.ru/cons/cgi/online.cgi?req=doc;base=ESU;n=15893 (дата обращения: 13.05.2014).
Отчет о научно-исследовательской работе по государственному контракту от 30.06.2011 г. № р-6к-11/4 Лот 4 «Разработка технологии повышения эффективности организации лесного хозяйства на основе системы рубок ухода за лесом» (фрагмент) // ФБУ «СПбНИИЛХ». URL: http://www.spb-niilh.ru/pdf/Prilozhenie1.pdf (дата обращения: 22.07.2014).
Приказ Федерального агентства лесного хозяйства (Рослесхоз) от 27.05.2011 г. № 191 «Об утверждении Порядка исчисления расчетной лесосеки» (зарегистрирован в Минюсте РФ 06.07.2011 г. № 21276) // Интернет-портал «Российской Газеты». URL: http://www.rg.ru/2011/07/07/lesoseka-site-dok.html (дата обращения: 13.05.2014).
Свалов Н. Н. Моделирование производительности древостоев и теория лесопользования . М.: Лесн. пром-сть, 1979. 216 с.
Синицын С. Г., Моисеев Н. А., Загреев В. В. и др. Расчет размера лесопользования . М.: Лесн. пром-сть, 1973. 176 с.
Спелость леса // Яндекс словари. URL: http://slovari.yandex.ru/~книги/БСЭ/Спелость леса/ (дата обращения: 13.05.2014).
Что такое расчетная лесосека, и обеспечивает ли она неистощительное лесопользование? // Wood.ru – Первый лесопромышленный портал. URL: http://www.wood.ru/ru/loa298.html (дата обращения: 22.07.2014).
Швиденко А. З., Щепащенко Д. Г., Нильссон С., Булуй Ю. И. Таблицы и модели хода роста и продуктивности насаждений основных лесообразующих пород Северной Евразии (нормативно-справочные материалы) . М.: Федеральное агентство лесного хозяйства, 2008. 886 с.
Ярошенко А. Ю. К вопросу об определении объемов неистощительного лесопользования // Лесной форум Гринпис России. URL: http://www.forestforum.ru/viewtopic.php?p=94107 (дата обращения: 22.07.2014).
JavaScript // Википедия – свободная энциклопедия. URL: http://ru.wikipedia.org/wiki/JavaScript (дата обращения: 13.05.2014).
Forest Finland in Brief 2013 / ed. Yrjö Sevola; Finnish Forest Research Institute, METLA. Vantaa: Kopijyvä, 2013. 48 p.
Благодарности
Исследование выполнено при поддержке проекта WWF и IKEA «Содействие устойчивому лесопользованию в России на основе сотрудничества со всеми заинтересованными сторонами в сферах государственного управления, бизнеса и образования».
Авторы благодарят координатора проектов по лесам высокой природоохранной ценности WWF России Кобякова Константина Николаевича за инициирование размышлений по проблемам исчисления параметров расчетной лесосеки неистощительного пользования и активное участие в обсуждении полученных результатов.
Авторы будут признательны за любые комментарии и замечания по существу разработанного подхода.






 © 2011 - 2026
© 2011 - 2026