Введение
Проблема необходимости учета влияния сопутствующих переменных при анализе экспериментальных данных в медицине и экологии была осознана достаточно давно. В простейшей форме эта проблема появляется как несравнимость экспериментальных групп, различающихся по сопутствующим переменным. Так, в 1747 г. шотландский врач James Lind (1716–1794) при оценке сравнительной эффективности средств от цинги явно сформулировал возможность сравнения тех экспериментальных пар моряков, для которых были одинаковы такие характеристики, как стадия болезни, пища, качество воздуха (Lind, 1953; Tröhler, 2003; Morabia, 2004; Morabia, 2011).
В XIX в. несравнимость групп в эпидемиологических исследованиях чаще всего воспринималась как непреодолимое препятствие, и только в первой половине XX в. были предложены методы для ее решения: рандомизация (Therapeutic…, 1934), цензурирование выборки (Goldberger et al., 1920), стандартизация, предсказываемые вероятности относительно воздействия – exposure propensity scores (Weinberg, 1913; Lane-Claypon, 1926; Winkelstein, 2004). Тем не менее корректного решения этой проблемы, которое устроило бы всех исследователей, не существует до сих пор (Vandenbroucke, 2004).
В настоящей работе проблема учета сопутствующих переменных (конфаундеров) обсуждается для специального случая сравнительных исследований (сравнение результатов для опытной и контрольной групп), которые являются частым случаем многих задач в экологии и экологической медицине (Anderson et al., 1980). Из множества методов решения проблемы конфаундеров в настоящей статье обсуждаются два наиболее популярных метода: классическая процедура стандартизации и статистическое моделирование методами регрессионного анализа. В работе предлагается новая автоматизированная процедура стандартизации, с помощью которой проведено сравнение результатов стандартизации и результатов статистического моделирования регрессионными методами.
Аналитический обзор
Терминология
Сравнительные исследования (Comparative studies) – это исследования, в которых сравниваются результаты, полученные на двух группах объектов. Одна группа традиционно называется «опытная группа» (treatment group) – это группа объектов, которые подвергаются некоторому воздействию (treatment); объекты второй группы («контрольная» группа, control group) не подвергаются данному воздействию. Задача сравнительного исследования состоит в определении влияния воздействия на выбранную исследователем характеристику изучаемых объектов. Эту характеристику называют «Отклик на воздействие» или просто «Отклик» (outcome, response). Разность откликов в опытной и контрольной группах называют эффектом воздействия (Anderson et al., 1980).
Фактор риска. В экологических и эколого-медицинских исследованиях воздействие обычно ассоциируется с некоторым фактором риска (risk factor – RF). Например, при изучении влияния на экологическую систему загрязнения окружающей среды в качестве опытной территории выбирают территорию с «условно высоким» уровнем загрязнения окружающей среды, а в качестве контрольной – условно «чистую» территорию, на которой это загрязнение отсутствует или незначительно. Объекты экологической системы (растения, животные, человек) на опытной территории (обозначим эту территорию как RF = 1, т. е. территория, на которую действует фактор риска RF) подвергаются неблагоприятному воздействию поллютантов, в результате чего некоторая характеристика Y изучаемых объектов изменяется по сравнению с этой же величиной Y для объектов контрольной группы (RF = 0). В качестве отклика системы на воздействие обычно принимают значение Y, усредненное по всем объектам группы (Ῡ). Тогда эффект воздействия, равный разности откликов в опытной и контрольной группах, равен
ΔY(RF) = Ῡ(RF = 1) – Ῡ(RF = 0). [1]
Конфаундер, контроль конфаундеров. Кроме фактора риска (основной изучаемый фактор) объекты исследования могут характеризоваться рядом других факторов (так называемые «сопутствующие факторы» Х), влияние которых на отклик Y может исказить эффект фактора риска RF, т. е. природа сопутствующих факторов может быть такой, что часть изменчивости отклика может объясняться изменчивостью сопутствующих факторов, а не влиянием фактора риска. Казалось бы, можно построить экспериментальное исследование таким образом, чтобы сопутствующие переменные не оказывали влияние на отклик, однако особенности конфаундеров именно в том, что они неустранимы. Например, невозможно устранить влияние таких факторов, как пол или возраст, при исследовании человеческой популяции, а пренебрегать ими не всегда возможно, т. к. они имеют заметное влияние на исследуемый отклик.
Именно такие неустранимые факторы называют конфаундерами (confounding factors, confounders). Согласно определению (Bonita et al., 2006), сопутствующий фактор Х является конфаундером, если он удовлетворяет двум условиям: 1) фактор Х оказывает влияние на отклик Y; 2) распределения фактора Х в группах с различными уровнями RF различны. Эти два условия можно перевести на математический язык следующим образом: сопутствующий фактор Х является конфаундером для фактора риска RF, если Х имеет статистически значимую связь как с Y, так и с RF.
Смещение. Искажающее влияние конфаундера Х на эффект, производимый основным исследуемым фактором риска RF, называют confounding, а величину искажения эффекта – смещением (bias). Задача исследователя заключается в том, чтобы устранить (уменьшить) смещение, т. е. определить максимально «точно» эффект именно фактора риска RF, отделив его от искажающего влияния конфаундера. Процедуры, которые позволяют «выделить» эффект фактора риска на фоне действующих конфаундеров, обобщенно называют «Контроль конфаундеров» или «Учет конфаундеров» (сontrol for confounders, accounting for confounders, methods to adjust for confounders) (Anderson et al., 1980; Bonita et al., 2006).
Например, в экологическом исследовании изучается влияние RF на некоторую характеристику объектов Y, причем Y зависит от сопутствующего фактора, например от возраста объектов Х. Пусть возраст объектов в одной группе отличается в среднем от возраста объектов в другой группе. При таких условиях, согласно приведенному выше определению, возраст Х является конфаундером для фактора риска RF. Примем для определенности, что Y увеличивается с увеличением Х и среднее значение Х в опытной группе выше, чем в контрольной. Понятно, что при этих условиях различие возрастов в группах RF = 0 и RF = 1 будет увеличивать эффект ΔY(RF), в противном случае (возраст в опыте меньше, чем в контроле) – уменьшать эффект изучаемого фактора риска RF.
Методы контроля (учета) конфаундеров
Контроль за влиянием конфаундеров возможен как на этапе планирования экспериментальных исследований, так и на этапе анализа данных. Методы контроля конфаундеров на этапе планирования (общее название методов – уравнивание, англ. Matching) в данной работе не рассматриваются; они подробно описаны, например, в монографиях (Anderson et al., 1980; Bhopal, 2002; de Graaf et al., 2011). Методы контроля конфаундеров на этапе анализа данных (общее название методов – подгонка, корректировка, англ. Adjustment procedure или просто adjustment) делятся на две группы: 1) методы стандартизации путем стратификации массива данных; 2) методы, основанные на статистических моделях. Именно методы учета конфаундеров на этапе анализа являются предметом исследования настоящей работы.
В общем виде назначение любых процедур учета конфаундеров на этапе анализа данных (Adjustment procedure) состоит в устранении различий в распределениях конфаундеров Х в опытной и контрольной группах. С математической точки зрения такое устранение различий приводит к тому, что Х перестает коррелировать с фактором риска RF и, следовательно, сопутствующий фактор Х перестает быть конфаундером (т. е. не может искажать эффект ΔY(RF) изучаемого RF).
В следующих подразделах описаны два метода контроля (учета) конфаундеров. Первый из них – процедура стандартизации, являющаяся одним из вариантов процедуры контроля конфаундеров на этапе анализа данных. Второй – процедура контроля конфаундеров с помощью регрессионных моделей.
Стандартизация в сравнительных исследованиях
Пусть некоторая характеристика Y (отклик) измеряется на объектах двух групп, разделенных по фактору риска (RF = 0 и RF = 1), т. е. мы имеем случай сравнительного исследования влияния фактора риска RF на отклик Y; изучаемые объекты характеризуются набором сопутствующих переменных Х, влияние которых на Y может исказить эффект исследуемого фактора риска. Задача состоит в корректном определении величины эффекта фактора риска ΔY(RF), определяемого формулой [1].
Один из классических способов устранения искажающего влияния конфаундера – стандартизация путем стратификации массива наблюдений (Weinberg, 1913; Goldberger et al., 1920; Bhopal, 2002; Власов, 2004). Ниже мы рассмотрим процедуру так называемой прямой стандартизации (наиболее распространенная из процедур, основанных на стратификации); описание других приемов стандартизации можно найти в монографии (Anderson et al., 1980, глава 7). Техническое исполнение процедуры прямой стандартизации (в дальнейшем будем использовать термин «Стандартизация») проиллюстрируем на следующем примере.
Пусть ставится задача определения влияния загрязнения территории проживания на здоровье населения (фактор риска RF – загрязнение территории). Это типичная эколого-эпидемиологическая задача, суть которой понятна даже неспециалисту в области экологии или эпидемиологии. Для решения этой задачи выбираются две территории (например, два города), один из которых можно считать «условно чистым» (RF = 0), второй – загрязненным (RF = 1). В двух городах собираются сведения о заболеваемости населения и рассчитываются средние значения заболеваемости Ῡ(RF = 0) и Ῡ(RF = 1). В гипотетическом случае отсутствия конфаундеров разность этих средних дает ожидаемый эффект (эффект влияния загрязнения на заболеваемость).
В описанном выше примере появление конфаундеров – неизбежная плата за невозможность постановки активного эксперимента (исследователь может лишь фиксировать имеющиеся уровни загрязнения и заболеваемости, но не изменять их). Одним из типичных конфаундеров в описанной задаче является возраст. Предположим, что в задаче определения влияния загрязнения на здоровье «чистый» город является «спальным» районом мегаполиса, в котором живет значительная доля пожилого населения, а город с сильным загрязнением территории – промышленный город с высокой долей молодого населения. Поскольку заболеваемость населения, очевидно, увеличивается с возрастом, заболеваемость в «чистом» городе будет повышена за счет высокой доли пожилых людей, а в промышленном городе – понижена за счет молодой части населения и повышена вследствие загрязнения среды обитания. В этом случае эффект фактора риска «Загрязнение территории» будет снижен (относительно «истинного») за счет различий в возрастных структурах населения этих двух городов.
Процедура стандартизации путем стратификации данных предполагает разделение населения обоих городов на одинаковые слои (страты) по возрасту, например по 10 лет. В каждой страте определяется численность населения ni(RF = 0), ni(RF = 1) и средняя заболеваемость населения каждого города отдельно Ῡi(RF = 0), Ῡi (RF = 1), где i – номер страты. Эффект от загрязнения без учета возраста (конфаундера) определяется по формуле (Bonita et al., 2006, Вараксин и др. 2012)
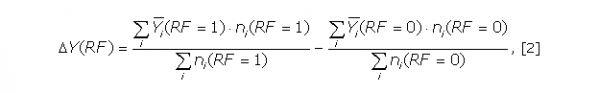
в которой суммирование идет по всем возрастным стратам.
Формула [2] является вариантом представления формулы [1] с учетом стратификации данных, полностью ей эквивалентна и дает тот же результат. Расчет эффекта загрязнения территории с учетом возраста (стандартизация по возрасту) осуществляется по формуле
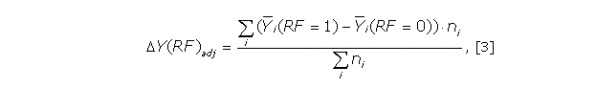
где нижний индекс adj означает adjustment (подгонка). Формула [3] отличается от [2] тем, что в [2] отклики Ῡi(RF = 0) и Ῡi(RF = 1), рассчитанные для i-й страты, суммируются с весами ni(RF = 0) и ni(RF = 1), которые различаются для групп RF = 0 и RF = 1, а в [3] веса ni для групп RF = 0 и RF = 1 – одинаковы. Именно таким образом устраняются различия в распределении возрастов в опытной и контрольной группах и «устраняется» искажающее влияние возраста на ΔY(RF).
Показывая формальный путь устранения влияния конфаундера, процедура стандартизации не дает однозначного ответа на вопрос, как выбрать численные значения весов ni в формуле [3]. Несколько часто встречающихся вариантов для рассмотренного выше примера таковы:
a) численности ni равны средней численности населения в опытной и контрольной группах для i-й страты
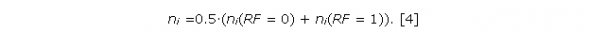
б) численности ni выбираются равными численностям населения в i-й возрастной группе для целого региона, в котором расположены «чистый» и загрязненный города; вместо региональной можно выбрать возрастную структуру страны в целом, мировую возрастную структуру и т. п.
Очевидно, что каждый вариант выбора ni приводит к разным результатам при оценке эффекта ΔY(RF). В разделе «Заключение» мы дадим комментарии этой неоднозначности оценки ΔY(RF). Кроме ni, эффект ΔY(RF) будет также зависеть от способа разделения массива наблюдений на страты (число страт и их границы), поэтому предметная трактовка полученных скорректированных (adjusted) значений эффекта ΔY(RF) зависит от содержательного смысла выбранных страт и их численностей ni.
При выполнении процедуры стандартизации действует ограничение: процедура осуществима при условии, когда обе численности ni(RF = 0) и ni(RF = 1) отличны от нуля для каждой i-й страты; в случае нулевого значения ni(RF = 0) либо ni(RF = 1) данная i-я страта должна быть полностью исключена из анализа вследствие невозможности рассчитать один из откликов Ῡi(RF = 0) либо Ῡi(RF = 1), для которого ni(RF) = 0. Впрочем, есть возможность не терять эти данные, если выбрать иные границы страт таким образом, чтобы ни одна из них не оказалась пустой.
Статистические методы контроля конфаундеров
Процедура стандартизации является ясной и предметно-понятной процедурой учета конфаундеров. Единственный недостаток процедуры стандартизации – трудность практической реализации при наличии многих конфаундеров. Чтобы преодолеть эту трудность, было предложено использовать методы статистического моделирования. Одной из первых публикаций в этом направлении является работа Рональда Фишера (Фишер, 1958), в которой рассматривается применение методов ковариационного анализа. В 1957 г. специальный выпуск журнала Biometrics (Vol. 13 (3)) был посвящен ковариационному анализу и его применениям; в этом выпуске поднимался вопрос и о конфаундерах (variable for adjustment). По-видимому, переход к другим статистическим моделям как средству учета конфаундеров был сделан именно через ковариационный анализ. В результате для учета конфаундеров стали применяться регрессионные модели (линейные и логистические), которые в некоторых областях экологии и эпидемиологии стали основными (Miettinen, 1976; Stein et al., 2013).
Рассмотрим применение методов статистического моделирования на примере бинарного отклика Y, когда Y принимает два значения Y = 0 и Y = 1 (в случае заболеваний эти два значения Y соответствуют градациям «здоров» и «болен»). В этом случае стандартным методом статистического моделирования является логистическая регрессия.
Контроль конфаундеров методом логистической регрессии проводится следующим образом. По экспериментальным данным строится уравнение логистической регрессии, описывающее эффект фактора риска RF
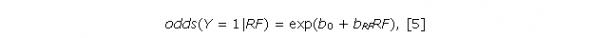
где odds(Y = 1|RF) – шанс появления значения Y = 1 (шанс заболеть). Показателем эффекта, производимого фактором риска RF, в логистической регрессии является отношение шансов (OR) – отношение шанса заболеть при наличии фактора риска odds(Y = 1|RF = 1) к шансу заболеть при отсутствии фактора риска odds(Y = 1|RF = 0). Согласно теории логистической регрессии, искомое отношение шансов рассчитывается по формуле (Hosmer et al., 2002):
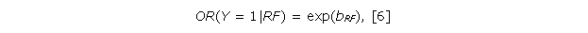
где bRF – коэффициент уравнения [5].
При наличии конфаундеров их контроль производится путем включения в уравнение [5] имеющихся конфаундеров Х1, Х2, …, Xk, т. е. путем построения уравнения множественной логистической регрессии:
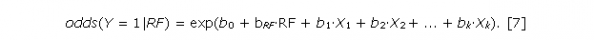
Включение конфаундеров в уравнение логистической регрессии приводит к изменению значения коэффициента bRF при факторе риска RF (значение bRF заменяется на b*RF); это изменение трактуется как учет конфаундеров при расчете эффекта фактора риска RF (Hosmer et al., 2002; Bonita et al., 2006; van Stralen et al., 2010; Tripepi et al., 2011).
Аналогичным образом описывается в (Bonita et al., 2006; van Stralen et al., 2010; Tripepi et al., 2011) случай количественного отклика Y, когда вместо логистической регрессии используется линейная регрессия:
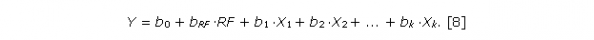
Описанная процедура контроля конфаундеров с использованием логистической регрессии является очень популярной в эпидемиологических исследованиях. Например, описанная процедура является практически единственной, принятой для использования авторами авторитетного журнала Epidemiology, который позиционирует себя не только как медицинский журнал (эпидемиология – наука о распространении массовых заболеваний), но и как журнал для публикации исследований в области прикладной статистики (Statistical Science Web, 2014). При этом стандартизация и статистическое моделирование рассматриваются многими современными авторами как два равноправных подхода для учета конфаундеров, хотя равносильность этих двух подходов не доказана и, по-видимому, основана на вере в то, что корректность применения подобной процедуры в форме ковариационного анализа сохраняется и для общих регрессионных моделей. По нашему мнению, имеются веские аргументы против такого метода учета конфаундеров (Вараксин и др., 2011; Austin, 2011). Во-первых, нет доказательств того, что метод логистической регрессии действительно устраняет (уменьшает) различия в распределениях конфаундера в изучаемых группах RF = 0 и RF = 1. Во-вторых, изменение коэффициента bRF в уравнениях [5]–[6] при переходе к [7] может происходить в отсутствие корреляционной связи между конфаундером Х и откликом Y (просто за счет наличия корреляционных связей между Х и RF). Согласно введенному выше определению, отсутствие связи между Х и Y «выводит» сопутствующий фактор Х из разряда конфаундеров. Учитывая, что в практических исследованиях специальная проверка того, что переменная Х является конфаундером, проводится не всегда (чаще всего не проводится!), изменение коэффициентов регрессии bRF после добавления Х может создать неправильное представление о переменной Х как о конфаундере в ситуации, когда Х таковым не является.
Сравнение результатов контроля конфаундеров, полученных путем стандартизации и регрессионных моделей
Проведем сравнение результатов контроля конфаундеров, полученных путем стандартизации, методом логистической регрессии и ковариационного анализа.
Как отмечалось выше, равносильность двух подходов учета конфаундеров (стандартизация и регрессионное моделирование) требует доказательств. Однако провести формальное доказательство этого довольно трудно, учитывая статистическую природу обоих методов. В то же время доказательство их неэквивалентности можно построить точно так же, как в математической статистике проверяются статистические гипотезы: необходимо выбрать ситуацию, когда возможно применить оба метода учета конфаундеров, и показать, что при анализе этой ситуации оба метода дают разные результаты. Если результаты, полученные методами стандартизации и регрессионного анализа, не совпадают, это будет доказательством неприменимости метода логистической регрессии.
При сопоставлении двух подходов появляются затруднения, связанные с неоднозначностью процедуры стратификации (разделение массива наблюдения на страты, как было описано выше). Чтобы преодолеть эти неоднозначности, нами предложен алгоритм, минимизирующий различия в распределениях конфаундера Х в группах по фактору риска и, следовательно, уменьшающий смещение оценки эффекта ΔY(RF).
Суть алгоритма следующая. Проведем упорядочение значений Х для всех объектов исследования. Выбираем первое (минимальное) значение Х и определяем его принадлежность к группе RF = 0 или RF = 1. Выбираем следующее значение Х и также определяем его принадлежность к группе по фактору риска. Если первое и второе значения Х принадлежат к разным группам (например, первое значение Х принадлежит к группе RF = 0, а второе значение Х – к группе RF = 1), считаем, что эти два значения образуют первую страту. Если оба значения Х принадлежат к одной группе, выбираем третье значение Х и т. д. до тех пор, пока в выборке не окажутся объекты сразу двух групп (хотя бы один объект в каждой группе по RF). Минимальное число объектов n1, удовлетворяющих этому условию, составляют первую страту (i = 1). Для объектов этой страты можно вычислить среднее значение отклика Y в группах по фактору риска; это будут Ῡ1 (RF = 0) и Ῡ1 (RF = 1). Продолжая описанную процедуру вплоть до достижения максимального значения Х, получаем все необходимые данные для расчета эффекта ΔY(RF) по формуле [3].
Такой способ разделения на страты минимизирует различия распределений конфаундера Х в группах по фактору риска, поскольку средние значения конфаундера в опыте и контроле различаются минимально именно при минимальных размерах страт. Выбор в качестве ni численностей «объединенных» страт (объекты обоих групп по RF) соответствует условию [4] и кажется естественным в описанной ситуации. Дополнительным преимуществом описанного алгоритма является возможность его компьютерной реализации, что избавляет пользователя от необходимости ручных расчетов (несложных, но утомительных). Такая реализация была нами выполнена, и созданная компьютерная программа стандартизации «Программа для контроля конфаундеров при изучении действия факторов риска в задачах экологии человека» с описанием способа применения доступна на сайте Института промышленной экологии УрО РАН (http://www.iie-uran.ru). Для выполнения процедуры стандартизации необходимо запустить компьютерную программу, указать в базе данных имена переменных отклика Y, фактора риска RF и конфаундера X; все остальное выполняется компьютерной программой автоматически.
Проведем сравнение методов стандартизации, логистической регрессии и ковариационного анализа на примере реальных данных 861 жителя Свердловской области, у которого специалистом-кардиологом проведено определение состояния сердечно-сосудистой системы (ССС) и изучается влияние на развитие патологии ССС таких факторов, как возраст, артериальное давление и метеотропные реакции (база данных Института промышленной экологии УрО РАН, 1994 (Вараксин и др., 2011)). В приведенных ниже расчетах откликом Y является показатель состояния ССС (здоровые Y = 0 и лица с явными проявлениями сердечно-сосудистых заболеваний Y = 1), фактором риска RF считается показатель «Метеотропные реакции» (человек отмечает у себя наличие/отсутствие реакций на изменение погоды), конфаундерами являются «Возраст» и «Диастолическое артериальное давление» (ДАД). Поскольку наш алгоритм стандартизации работает только с одним конфаундером, возраст и ДАД выступают конфаундерами в двух отдельных расчетах.
Начнем с оценки степени влияния фактора риска без учета конфаундеров. Эффект фактора риска «Метеотропные реакции» выражается отношением шансов OR = 7.1 (95 %-й доверительный интервал: 5.2–9.7). В соответствии с обычной трактовкой отношения шансов отсюда можно сделать вывод, что метеотропные реакции являются значимым фактором риска развития сердечно-сосудистых патологий.
При изучении влияния метеотропных реакций на появление заболеваний ССС конфаундерами могут выступать такие сопутствующие факторы, как возраст и артериальное давление. Проверка условий того, что факторы являются конфаундерами, показывает следующее. Для фактора «Возраст» среднее значение в группе «Здоровые» (отклик Y = 0) равно 33.3 года, в группе «Больные» (отклик Y = 1) – 52.9 года. Различие этих средних значений является статистически значимым по критерию Стьюдента (p < 0.00001), следовательно, имеется статистически значимая связь между откликом Y и сопутствующим фактором «Возраст». Аналогично среднее значение возраста в группе RF = 0 «Нет метеотропных реакций» равно 36.7 года, в группе RF = 1 «Есть метеотропные реакции» – 52.1 года. Различие средних значений является статистически значимым по критерию Стьюдента (p < 0.00001), следовательно, имеется статистически значимая связь между фактором риска RF и сопутствующим фактором «Возраст». Таким образом, фактор «Возраст» удовлетворяет обоим условиям, необходимым для того, чтобы быть конфаундером при изучении связи распространенности заболеваний ССС и метеотропных реакций.
Что касается фактора «Диастолическое артериальное давление», среднее значение в группе «Здоровые» (отклик Y = 0) равно 77.9 мм рт. ст., в группе «Больные» (отклик Y = 1) – 89.5; среднее значение ДАД в группе RF = 0 равно 82.6 мм рт. ст., в группе RF = 1 – 87.3 мм рт. ст. Различия средних значений являются статистически значимыми по критерию Стьюдента (p < 0.00001), следовательно, показатель ДАД является конфаундером при изучении связи распространенности заболеваний ССС и метеотропных реакций.
Таблица. Примеры применения программы стандартизации и сравнение результатов стандартизации с логистической регрессией и ковариационным анализом
Table. Examples of application of standardization program and comparison of standardization, logistic regression and analysis of covariance results
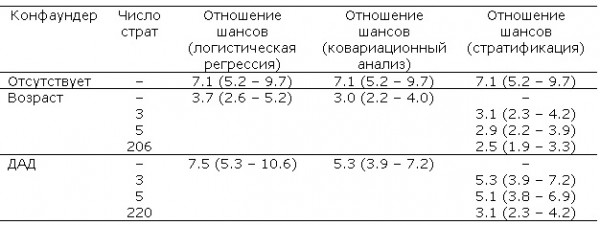
Как показывают данные таблицы, применение процедуры стандартизации понижает эффект фактора риска: в случае конфаундера «Возраст» отношение шансов уменьшается в 7.1 / 2.5 = 2.8 раза, в случае конфаундера «Диастолическое давление» в 7.1 / 3.1 = 2.3 раза. В то же время учет конфаундера методом логистической регрессии дает разнонаправленные результаты для двух конфаундеров. Для конфаундера «Возраст» логистическая регрессия дает OR = 3.7; это значение OR попадает в 95%-й доверительный интервал для OR, рассчитанного методом стандартизации. Для конфаундера «Диастолическое давление» процедура стандартизации и логистическая регрессия дают принципиально различные «сдвиги»: стандартизация уменьшает отношение шансов (т. е. эффект фактора «Метеотропные реакции» снижается в результате учета конфаундера ДАД), в то время как метод логистической регрессии предсказывает повышение отношения шансов. Расчет отношения шансов OR методом ковариационного анализа и в случае конфаундера «Возраст», и в случае конфаундера «Диастолическое давление» показывает значения, практически совпадающие со значением OR, получаемым при стратификации с малым числом страт (3 страты). Заметим, что дисперсионный анализ, применяемый для сопоставления средних значений в группах, образованных всевозможными сочетаниями уровней действующих факторов, в контексте проблемы учета конфаундеров можно рассматривать как специальный вид стандартизации, при котором выбор страт происходит естественной стратификацией выборки по сочетаниям уровней факторов, а значения кратностей в формуле [2] определяются фактическими объемами полученных страт.
Таким образом, в некоторых случаях поправка изучаемого эффекта на конфаундер, полученная методом стандартизации, кардинально отличается (даже знаком) от поправки, рассчитанной методом логистической регрессии. Поскольку процедура стандартизации является предметно-обоснованным методом учета конфаундеров, отличие от нее результатов применения логистической регрессии показывает неприемлемость этого метода учета конфаундеров как безусловного аналога стандартизации. Вообще говоря, возможны случаи, когда применение обоих методов (стандартизации и логистической регрессии) дает качественно согласованные результаты, но предсказать, когда это будет именно так, а не иначе, не представляется возможным. Более того, даже при качественном согласовании будут сохраняться количественные различия результатов учета конфаундеров обоими методами (например, в форме различия величин отношения шансов), и это может создать проблемы с интерпретацией результатов расчета.
Проблема учета влияния конфаундеров в сравнительных исследованиях является давно осознанной, предложены различные методы ее решения. Их можно разделить на два методологически различных класса: учет конфаундеров на стадии планирования эксперимента и учет конфаундеров на этапе анализа данных (при анализе соответствующей статистической модели). Первый способ применим только при активном (постановочном) эксперименте, что редко встречается в эколого-медицинских исследованиях. Второй способ предполагает возможность корректного учета конфаундеров некоторыми вычислительными процедурами.
Технически процедура учета конфаундеров в статистических моделях состоит в том, что сравниваются значения коэффициентов при основном изучаемом факторе для моделей с конфаундерами и без них. Изменение коэффициентов модели при включении в нее конфаундеров не является следствием какого-либо варианта стандартизации, а происходит в результате чисто вычислительной процедуры аппроксимации модели (например, методом наименьших квадратов или методом наибольшего правдоподобия). Любая такая процедура a priori принимает все имеющиеся переменные равнозначно и, следовательно, изменение коэффициента при основном исследуемом факторе отражает аппроксимационные качества статистической модели в целом, а не только вклад данной переменной. В частности, нет оснований для того, чтобы считать, что в результате такой модификации параметров модели происходит нечто подобное стандартизации, например выравнивание распределений конфаундера в группах по уровням фактора риска.
На основании представленного анализа мы считаем, что следует избегать применения статистических моделей регрессионного типа для учета конфаундеров и использовать их только в том случае, когда корректность такого применения предварительно доказана, что не всегда возможно.
Заключение
Если Х является конфаундером для фактора риска RF (Х влияет на Y и статистически связан с RF), задача «избавиться» от влияния конфаундера Х на ΔY(RF) является невыполнимой в принципе (как избавиться от влияния Х на Y, если это влияние реально существует?). Из изложенного выше следует, что устранение влияния конфаундера сводится, в конечном счете, к некоторому «договору», согласно которому эффект ΔY(RF) рассчитывается при некоторых условиях, накладываемых на конфаундер. Например, если конфаундером в рассмотренных выше примерах является возраст, мы делаем попытку оценить величину эффекта ΔY(RF) в «гипотетической» ситуации, когда распределения возрастов объектов в опытной и контрольной группах не различаются. При этом результат расчета эффекта ΔY(RF) будет явно зависеть от того, какое конкретное распределение объектов по возрастам мы выберем в процедуре стандартизации. Выбирая разные распределения, получим разные значения эффекта ΔY(RF). Следовательно, процедура поправки на конфаундер – это не способ избавиться от конфаундера, а некая форма «договора» с ним. Таким образом, при публикации полученного результата (результата расчета эффекта ΔY(RF) изучаемого фактора риска RF) декларация «договора» является обязательной. В противном случае остается неопределенность, которая сильно снижает достоверность полученных результатов.
Библиография
Вараксин А. Н., Панов В. Г., Константинова Е. Д. Некоторые подходы к статистическому анализу биологических и медицинских данных с конфаундерами // Экологические системы и приборы. 2012. № 7. С. 37–42.
Вараксин А. Н., Панов В. Г., Казмер Ю. И. Статистические модели с коррелированными предикторами в экологии и медицине . Екатеринбург: Изд-во Уральского университета, 2011. 144 с.
Власов В. В. Эпидемиология . М.: ГЭОТАР-Мед, 2004. 464 с.
Фишер Р. Э. Статистические методы для исследователей . М.: Госстатиздат, 1958. 268 с.
Anderson S., Auquier A., Hauck W.W., Oakes D., Vandaele W., Weisberg H.I. Statistical Methods for Comparative Studies. New York: Wiley, 1980. 289 p.
Austin P. An Introduction to Propensity Score Methods for Reducing the Effects of Confounding in Observational Studies // Multivariate Behavioral Research. 2011. № 46. P. 399–424.
Bhopal R. Concepts of Epidemiology: An integrated introduction to the ideas, theories, principles and methods of epidemiology. Oxford University Press, 2002. 317 p.
Bonita R., Beaglehole R., Kjellstrom K. Basic Epidemiology. WHO, 2006. 212 p.
De Graaf M. A., Jager K. J., Zoccali C., Dekker F. W. Matching, an Appealing Method to Avoid Confounding? // Nephron Clin Practice. 2011. Vol. 118. № 4. P. 315–318.
Goldberger J., Wheeler G. A., Sydenstricker E. A study of the relation of family income and other economic factors to pellagra incidence in seven cotton-mill villages of South Carolina in 1916 // Public Health Rep. 1920. № 35. P. 2673–2714.
Hosmer D. W., Lemeshow S. Applied logistic regression. 2nd ed. Wiley, 2000. 376 p.
Lane-Claypon J. A further report on cancer of the breast: reports on public health and medical subjects. London, UK: His Majesty’s Stationary Office, 1926. Report № 32. P. 1–189.
Lind J. A treatise of the scurvy, 1753. Edinburgh: University Press, 1953. 440 p.
Miettinen O. S. Stratification by a Multivariate Confounder Score // American Journal of Epidemiology. 1976. Vol. 104. № 6. P. 609–620.
Morabia A. History of the modern epidemiological concept of confounding // J Epidemiol Community Health. 2011. № 65. P. 297–300.
Morabia A. A history of epidemiological methods and concepts. Basel: Springer, 2004. 406 p.
Statistical Science Web: Main Journal List. URL: http://www.statsci.org/jourlist.html (дата обращения: 02.04.2014).
Stein C. R., Savitz D. A., Bellinger D. C. Perfluorooctanoate and Neuropsychological Outcomes in Children // Epidemiology. 2013. Vol. 24. № 4. P. 590–599.
Van Stralen K. J., Dekker F. W., Zoccali C., Jager K. J. Confounding // Nephron Clin Practice. 2010. Vol. 116. № 2. P. 143–147.
Therapeutic Trial Committee of the Medical Research Council. The serum treatment of lobar pneumonia // Lancet. 1934. № 1. P. 290–295.
Tripepi G., Jager K. J., Stel V. S., Dekker F. W., Zoccali C. How to Deal with Continuous and Dichotomic Outcomes in Epidemiological Research: Linear and Logistic Regression Analyses // Nephron Clin Practice. 2011. Vol. 118. № 4. P. 399–406.
Tröhler U. James Lind and scurvy: 1747 to 1795 // The James Lind Library. 2003. URL: http://www.jameslindlibrary.org (дата обращения: 03.04.2014).
Vandenbroucke J. P. The history of confounding. In: Morabia A., ed. History of epidemiological methods and concepts. Basel: Birkhäuser, 2004. P. 313–326.
Weinberg W. Die Kinder der Tuberkulosen. Leipzig: S. Hirzel, 1913. 160 p.
Winkelstein W. Jr. Vignettes of the History of Epidemiology: Three Firsts by Janet Elizabeth Lane-Claypon // Am J Epidemiol. 2004. Vol. 160. P. 97–101.
Благодарности
Работа выполнена при поддержке Программы Президиума УрО РАН «Фундаментальные науки – медицине», грант № 12-П-2-1033.






 © 2011 - 2026
© 2011 - 2026