Коросов А. В. Смысл и применимость ядерных методов в экологических исследованиях // Принципы экологии. 2024. № 4. С. 59–90. DOI: 10.15393/j1.art.2024.15662

Выпуск № 4

Методы экологических исследований

pdf-версия статьи

57.087.1

Смысл и применимость ядерных методов в экологических исследованиях

Введение

В отечественных публикациях по экологии все чаще используются ядерные методы (Бельская и др., 2017; Середкин и др., 2019; Зайцев и др., 2021), которые зачастую рассматриваются как статистическая обработка данных, дающая вероятностную оценку распространения изучаемых явлений во времени и пространстве. Эти завышенные ожидания могут привести к не вполне адекватным выводам. Фактически непараметрические ядерные методы играют роль лишь технологических приемов, позволяющих «конденсировать» имеющуюся информацию, сглаживать или, напротив, контрастировать различия между биологическими объектами в разные временные периоды или из разных географических областей (в зависимости от поставленных задач). Это очень мощные методы, но нельзя от них ждать большего, чем они могут дать.

Информация, полученная при выполнении экологических исследований, зачастую страдает как избыточной вариативностью, так и пробелами в базах данных. Ядра, фильтры, сплайны и т. п. − все это звенья одной цепи, это приемы избавления от избыточной вариабильности, вычленения в полученных данных устойчивых отношений и зависимостей и вычисления на этой основе новых «сглаженных», а также «пропущенных» значений.

В обоих случаях необходимо вычислить некое новое значение изучаемой переменной в проблемной точке, ориентируясь на значения в соседних точках.

Методы «исправления» первичных данных в той или иной форме развиваются и применяются в разных дисциплинах и относительно разных предметов. Разведочный анализ (Тьюки, 1981), картография (Девис, 1990), улучшение изображений (Иванов и др., 2007; Варламова, Турсунов, 2023), фильтрация сигналов (Отнес, Эноксон, 1982; Давыдов, 2005), аппроксимация распределений и зависимостей (Dinardo, 2001), функциональный анализ (Босс, 2005), машинное обучение (Норкин, 2024) и другие направления исследований зачастую используют разную терминологию, теоретическую базу и цели, однако обнаруживают большое сходство в идеологии и технологии исправления изучаемых рядов данных.

В принципе, содержание нашего сообщения можно выразить следующей цитатой, относящейся к фильтрации изображений:

«...задано исходное полутоновое изображение A, ... интенсивности его пикселей A(x, y). Линейный фильтр определяется вещественнозначной функцией F, заданной на растре.

Данная функция называется ядром фильтра, а сама фильтрация производится при помощи операции дискретной свертки (взвешенного суммирования). Результатом служит изображение B» (Иванов и др., 2007, с. 144).

Дальнейшее изложение посвящено расшифровке, детализации и иллюстрации этих положений и терминов относительно одномерных данных: рядов, профилей, выборок.

Методы вычисления новых (сглаженных или заполняющих) значений меняются в зависимости от фактуры и объема данных, поставленных задач, требуемой точности и должны осознанно подбираться для каждого случая. В нашей работе представлен широкий, но не исчерпывающий спектр методов. В цели автора не входят ни полный обзор всех методов, ни рассмотрение их математической подоплеки. Главный акцент сделан на общности и преемственности логических основ этих разных методов, а также на практике их использования с помощью функций среды R (The R…, 2023). Все использованные функции представлены в базовых пакетах (base, stats).

Цель публикации состоит в том, чтобы познакомить читателей с технологиями «исправления» эмпирической информации путем ликвидации избыточной изменчивости и пробелов в данных в среде R.

Такие методы, как фильтрация, аппроксимация полиномами, сплайном, известны и используются в экологии очень давно, поэтому они помещены в раздел «Традиционные методы». Ядерные методы проникли в экологию относительно недавно, их описание нашло свое место в разделе «Оригинальные методы».

Материалы

Для иллюстрации применения методов использовались оригинальные авторские материалы, полученные в Карелии. Часть из них представляет собой показания температуры тела рептилий и температуры среды, полученных в полевых экспериментах с помощью температурных микрологгеров в августе 2018 г. (Карелия, N62.0828, E33.9701) (Коросов, Ганюшина, 2020). Температура фиксировалась через 1 мин., за сутки выполнялось 1440 замеров (файл "tve202280_5_10_46.csv"). Часть материалов − морфологические характеристики обыкновенных гадюк (файл "vip.csv"), отловленных на островах Кижского архипелага (N62.0834, E35.2163) (Коросов, 2010).

Традиционные методы исследований

Для решения проблемы сглаживания и подстановки данных можно использовать одни и те же алгоритмы − подстановку, фильтры, сплайны, регрессионные тренды, компонентный анализ, ядерные методы.

Формальная постановка проблемы состоит в следующем. Имеется набор из m значений переменной x, полученных для серии отдельных «шагов» (i = 1, 2, … m). Отдельными шагами можно считать координаты в пространстве, отсчеты во времени или просто индексы упорядоченных объектов (особей, проб). Зачастую отдельные отсчеты отстоят друг от друга на разное расстояние по шкале x, т. е. шаги не равномерные. Если шаги задать равномерными, то могут выявиться три проблемы. Для некоторых шагов i не будет значений x_i (пробелы). На других шагах накопится несколько значений x_i (повторы). Либо значения на соседних шагах (x_i и x_i+1) будут сильно отличаться друг от друга (варьирование).

Несмотря на дефицит или избыток данных, зачастую требуется дать характеристику главному тренду изменения исходного показателя x. Такая задача может решаться с помощью регрессионного анализа. Однако во многих случаях следует сначала изучить характер естественной структуры и динамики данных, прежде чем навязывать им тот или иной вариант аппроксимации или описания.

Итак, требуется ряд значений x (объемом m) преобразовать в такой ряд значений y, чтобы для каждого шага i из множества равномерных шагов i = 1:n получить по одному значению y_i: x_{i (m)} → y_{i (n)}. При этом удается избавиться от избыточной изменчивости (вместо группы варьирующих x получаем одно значение y), а также заполнить пропуски (вместо пробела на месте x_i на шаге i определяем величину y_i).

Все названные методы используют общий технический прием − «скользящее окно». Окно − это относительно небольшая группа соседних значений х (или интервал на шкале 0X), которые берутся для выполнения над ними той или иной операции с целью получить «сглаженное» значение y. Термин «скользящее» относится к процедуре перебора (просмотра) все новых и новых групп x при последовательном смещении окна на один шаг вправо (рис. 1). Обычно размер окна (обозначается h), число отобранных значений x, остается одинаковым на протяжении всей процедуры сглаживания. Кроме термина «окно» используются другие — апертура, маска, фильтр, ядро, которые в определенном смысле выступают синонимами.

Поскольку в поле зрения оказывается серия коротких отрезков ряда x, их можно поместить в таблицу как отдельные выборки и использовать для расчета y_i (см. рис. 1). Самый простой вариант − это расчет «скользящей средней» (см. рис. 1, mean). Другие методы по-иному используют подготовленную таблицу фрагментов исходного ряда в стремлении рассчитать более обоснованную характеристику центра окна.

 

Рис. 1. Схема работы скользящего окна (h = 5): из ряда динамики температуры тела (x) последовательно отбираются по 5 соседних значений, из которых формируется таблица для расчета сглаженных значений температуры тела (y)

Fig. 1. The scheme of operation of the sliding window (h = 5): 5 adjacent values are sequentially selected from a series of body temperature dynamics (x), from which a table is formed for calculating smoothed body temperature values (y)

 

  Подстановка

Эти методы отличаются от прочих тем, что никаких вычислений не производится, а в качестве искомого значения y_i берется некое реальное значение x_i из окрестностей точки i (...i-3, i-2, i-1, i, i+1, i+2, i+3...).

Прореживание

Один из самых простых приемов − прореживание. Сначала формируются индексы шагов i будущих значений, которые назначаются с существенно большим шагом в исходном массиве, т. е. число значений новой выборки будет меньше, чем в исходной. Затем отбираются значения признака x, соответствующие новым отсчетам: y_i = x_i.

Для отображения суточного хода температуры тела гадюки можно вместо 1440 поминутных значений взять значения через 20 мин. или через 60 мин., т. е. каждое 20-е или 60-е значение (рис. 2).

head(v<-read.csv("tve202280_5_10_46.csv" )) x<-round(v$tv[1:1440],) (i<-seq(1,1440,60)) ; y<-x[i] plot(x,type='b',col='grey',cex=.5) lines(i,y)

 

 

 

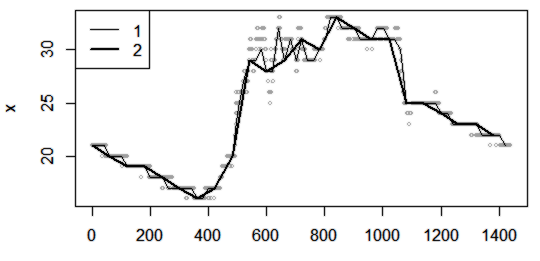
Рис. 2. Замена 1440 поминутных промеров температуры тела гадюки (x) значениями, взятыми через 20 мин. (1), через 60 мин. (2)

Fig. 2. Replacing 1440 minute-by-minute measurements of the viper's body temperature (x) with values taken after 20 min. (1), after 60 min. (2)

 

Для характеристики длины хвоста (lc = x[,2]) самок (f) гадюки с разной длиной тела (lt = x[,1]) можно взять только те промеры хвоста, которые попадают, например, в 50 интервалов, на которые разбита шкала длины тела. При этом сформируются 50 групп значений длины хвоста, соответствующих интервалам по длине тела. Из каждой группы можно выбрать либо случайное значение (таков метод подстановка с подбором внутри групп), либо медиану. Так сформируется ряд значений, соответствующих каждому интервалу, в котором резко снижена изменчивость и каждый центр получает определенное значение, соответствующее задачам сглаживания и заполнения пробелов. При использовании более широких интервалов значения существенно выравниваются (рис. 3). Случайный выбор числа из короткого ряда можно рассматривать как ядро (фильтр), в котором все члены (веса), кроме одного, равны нулю, а одно случайное значение равно единице. 

head(ve<-read.csv("vip.csv" ),2) f<-na.omit(ve[ve$S=='f',9:10]) x<-f[order(f[,2]),] ; lc<-x[,1] ; lt<-x[,2] s y<-rep(NA,s) for (i in 2:(s-1)){ y[i]<- # lc[which(lt>=dlt[i-1] & lt<=dlt[i+1])] [1] } median(lc[which(lt>=dlt[i-1] & lt<=dlt[i+1])] )} plot(lt,lc,col='grey',cex=.5) lines(dlt[1:s],y,type='l')

 

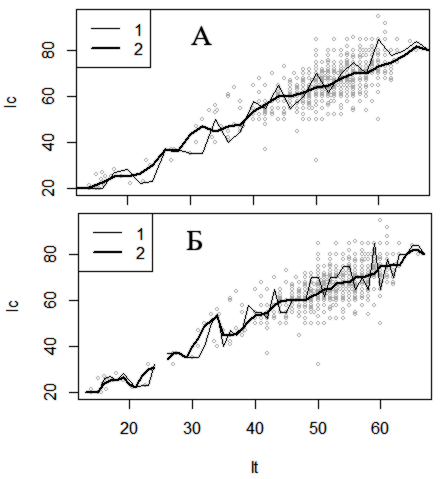  Рис. 3. Замена выборки единичным значением длины хвоста lc для шкалы длины тела lt, разбитой на 50 (А) и 80 (Б) интервалов: 1 − взяты случайные значения из групп, 2 − взяты медианные значения

Fig. 3. Replacing the sample with a single lc tail length value for the lt body length scale, divided into 50 (A) and 80 (Б) intervals: 1 − random values from the groups are taken, 2 − median values are taken

 

Широкий набор инструментов для подстановки множественной импутации, multivariate imputation) представлен в пакете mice среды R (Buuren, Groothuis-Oudshoorn, 2011).

Медиана

Второй прием состоит в том, чтобы очередное значение нового ряда y_i задавать как медиану из серии значений в окрестностях значения x_i (Тьюки, 1990). Для сглаживания по тройкам новое значение выбирается из трех (h = 3): y_i = med(x_i-1, x_i-1, x_i-1,); для сглаживания по пятеркам − из пяти (h = 3): y_i = median(x_i-2, x_i-1, x_i, x_i+1, x_i+2) и т. д.

Применяя метод скользящей медианы при сглаживании ряда значений по тройкам, в окне будут последовательно рассматриваться следующие наборы значений: y₂ = median(x₁, x₂, x₃), y₃ = median(x₂, x₃, x₄), y₄ = median(x₃, x₄, x₅) и т. д. После сглаживания всего ряда определяются краевые значения по формуле: y₁ = median(x₁, y₂, 3*y₂ − 2*y₃) (Тьюки, 1990, с. 228). В среде R функция runmed() выполняет подбор медиан для окон разной ширины. Функция smooth() возвращает медианы для разных правил сглаживания, представленных в (Тьюки, 1990). Функция smoothEnds() рассчитывает краевые значения по представленной выше формуле. Функция runmed() с аргументом endrule = c("median") выполняет обе эти операции и восстанавливает полный ряд.

Чем шире окно, тем более выравненным оказывается ряд результирующих медиан, тем результирующая кривая будет более гладкой и без разрывов (рис. 4). Скользящую медиану называют еще «нелинейным фильтром» (Иванов и др., 2007).

head(ve<-read.csv("tve202280_5_10_46.csv")) i<-seq(500,600) ; x<-ve[i,3] y1<-runmed(x, k=3, endrule = c("median")) y2<-runmed(x, k=7, endrule = c("median")) y3<-runmed(x, k=33, endrule = c("median")) plot(i,x,type='p',col='grey',lwd=5) lines(i,y1,lwd=1) ; lines(i,y2,lwd=2) ; lines(i,y3,lwd=4,col=2) legend('bottomright',lwd=c(1,2,4), col=c(1,1,2),legend=c(1,2,3))

 

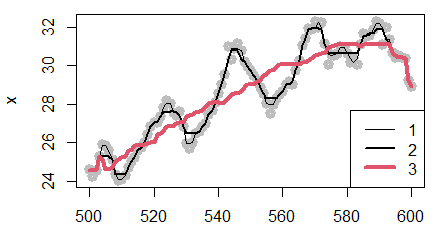
Рис. 4. Динамика скользящих медиан для температуры тела гадюки с 500-й по 600-ю минуту суток, определенных в окне шириной h = 3 (1), h = 7 (2), h = 33 (3) на фоне точек исходных данных

Fig. 4. Dynamics of sliding medians for the body temperature of the viper from 500 to 600 minutes of the day, defined in a window with widths h = 3 (1), h = 7 (2), h = 33 (3) against the background of the initial data points

 

Сглаживание взаимозависимых переменных обычно ведет к росту корреляции.

ve<-read.csv("tve202280_5_10_46.csv") i<-seq(500,600) ; xv<-ve[i,3] ; xo<-ve[i,4] yv<-runmed(xv, k=33, endrule = c("median")) yo<-runmed(xo, k=33, endrule = c("median")) cor(xv,xo) ; cor(yv,yo) [1] 0.8626159 [1] 0.9466184

 

Линейный фильтр

Фильтрация данных в общем смысле − это отбор записей из баз данных, удовлетворяющих заданным условиям.

Применительно к сглаживанию «фильтр» − это метод для усиления или подавления определенных частот входного сигнала (Отнес, Эноксон, 1982; Яновский, Буховец, 2015). Название «линейный фильтр» соответствует формуле для расчета новых значений y_i, в которой входные переменные и выход связаны линейными зависимостями. Самый известный фильтр − метод скользящей средней.

Окно фильтра (размером h = 3) скользит вдоль ряда x с шагом 1 и на каждом i-м шагу по трем значениям x рассчитывает новое сглаженное значение y_i:

y_i = Σ(x_i−1 , x_i, x_i+1 )/3.

Формулу можно переписать с использованием коэффициентов пропорциональности w, которые в сумме составляют единицу Σw_j = 1. Число весовых коэффициентов равно ширине окна (h). Средняя по тройкам для шага i равна (рис. 5):

y_i = 0.333*x_i−1 + 0.333*x_i + 0.333*x_i+1.

 

 

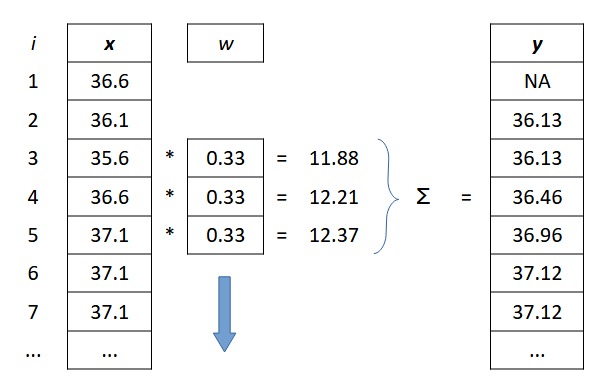
Рис. 5. Скользящая средняя: процесс расчета четвертого (i = 4) значения ряда y с использованием трех значений ряда x и трех значений фильтра w (h = 3)

Fig. 5. Moving average: the process of calculating the fourth (i = 4) value of the y series using three values of the x series and three values of the w filter (h = 3)

  

Для окон других размеров и формы выполняется расчет нового значения y_i для данного шага i с использованием серии значений x, попадающих в окрестности точки i (окна шириной h = 2N+1). Сглаженное значение y_i рассчитывается как сумма первичных значений x, входящих в окно, умноженных на весовые коэффициенты w (Σw_j = 1):

y_i = (w₁*x_i−N + … + w_j*x_i + … + w_h*x_i+N).

 В среде R линейную фильтрацию выполняет функция filter(). Функция возвращает ряд, укороченный слева и справа на величину N = (h − 1)/2. Причина состоит в том, что для расчета новых крайних значений y₁ и y_n, например, по тройкам требуются значения x₀ и x_n+1, которых нет в ряду. Вместо y₁ и y_n функция подставляет NA, т. е. длина выходного ряда y равна длине входного x, что удобно при построении графиков сглаженных линий.

Основные аргументы функции filter(x, filter) − это массив значений, которые нужно сгладить (x), и вектор весовых коэффициентов w (filter).

Функция позволяет использовать окна фильтра разной ширины и формы (рис. 6). Под формой фильтра понимается некое правило или функция, определяющая различие между весовыми коэффициентами в окне (Σw_j = 1). Фильтры разной формы подходят для решения разных задач. Например, если необходимо выявить самый общий характер хода данных, проще воспользоваться широким плоским (прямоугольным) фильтром с равными весовыми коэффициентами (рис. 7: 2). Если необходимо подчеркнуть крупные волны, лучше воспользоваться каким-либо выпуклым (например, параболическим) фильтром. В тех областях ряда x, которые по форме похожи на фильтр (гребень волны), новая переменная y получит высокие значения, а для понижений графика фильтр даст низкие оценки. В примере параболическая весовая функция Ланцоша более выразительно подчеркивает перепады в исходных данных, чем простая средняя (для h = 11) (рис. 7: 3). Исходя их различных теоретических соображений, предложен большой ряд различных весовых функций, используемых при том или ином варианте сглаживания рядов (Давыдов, 2005).

Ширина фильтра влияет на ход сглаженной кривой. Чем шире окно фильтра, тем более выравненной будет результирующая линия (см. рис. 7).

 

 Рис. 6. Формы окон фильтров: прямоугольное, треугольное, Шеппарда, Ланцоша

Fig. 6. Shapes of filter windows: rectangular, triangular, Shepard, Lanczos 

head(ve<-read.csv("tve202280_5_10_46.csv")) i<-seq(540,560) ; x<-ve[i,4] plot(i,x,cex=.5) h y1<-filter(x,w) h y2<-filter(x,w) lines(i,y1,lty=2) ; lines(i,y2) pro<-c(1,3,5,3,1) ; (w<-pro/sum(pro)) y3<-filter(x,w) lines(i,y3,lwd=2,col=2) legend('topleft',legend=c(1:3), lty=c(2,1,1),lwd=c(1,1,2),col=c(1,1,2))

  

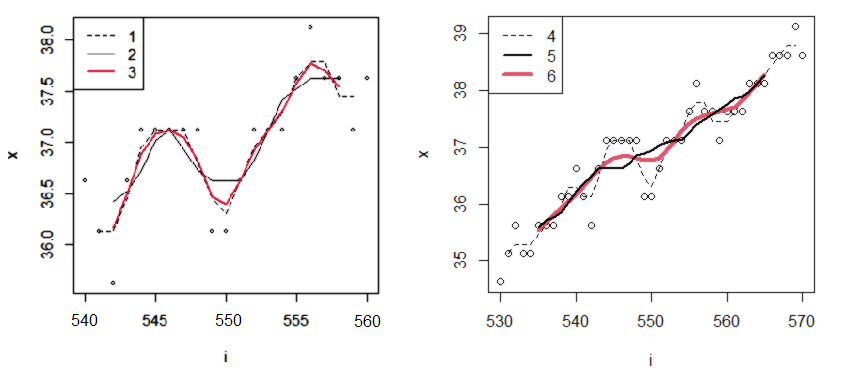
 Рис. 7. Ряды значений температуры, сглаженные разными фильтрами: 1 − плоский (h = 3), 2 − плоский (h = 5),         3 − треугольный (h = 5), 4 − плоский (h = 3), 5 − плоский (h = 11), 6 − параболический (Ланцоша ) (h = 11)

Fig. 7. Series of temperature values smoothed by different filters: 1 − flat (h = 3), 2 − flat (h = 5), 3 − triangular (h = 5),   4 − flat (h = 3), 5 − flat (h = 11), 6 − parabolic (Lanczos) (h = 11)

 

Достаточно простое понятие фильтра позволяет дать первичное определение некоторым терминам, которые понадобятся в дальнейшем.

 

Свертка

Понятие «свертка» используется для характеристики взаимного совпадения, или коррелированности, двух функций. Рисунок 5 в целом отражает эту процедуру − линейную дискретную свертку (Давыдов, 2005). При этом одна функция (w) смещается относительно другой (x) вдоль оси аргумента (i) и для всех совпадающих позиций по i отыскивается произведение значений функций (w*x). Результат интегрируется (в примере суммируется по тройкам, ∑(w*x)) и предстает как значение третьей функции (y) для каждого значения аргумента i.

Фильтрация − это свертка. В качестве первой функции выступает ряд значений x, в качестве второй функции выступают веса w, в качестве результирующей функции выступает ряд y. Эта процедура преобразования двух функций в одну выполняется при многих видах анализа, в т. ч. в ядерных методах, а также в некоторых видах нейронных сетей (в сверхточных нейронных сетях, CNN).

 

Ядро

В контексте процедуры сглаживания ядро − это набор коэффициентов фильтра, или, иначе, это та функция, которая используется для свертки другой функции. Можно считать, что совокупность весовых нагрузок w линейного фильтра − это и есть ядро, ядро фильтра. По сути, фильтр, ядро, ядерная функция, весовая функция − это синонимы.

 

Назначения весовой функции методом ближайших соседей

В рассмотренных случаях для фильтрации данных строились окна методом ближайшего соседа (Черненький, Птицын, 2005; Воронцов, 2009). Это значит, что весовые нагрузки для значений функции x назначаются, учитывая только порядковый номер значения x_i в упорядоченном ряду, т. е. с ориентацией на индекс i. В примере (табл. ОП. xw5, рис. 9: 1) для окна шириной h = 5 в расчет нового значения y_i включаются пять соседних значений x₇ = 27.0, x₈ = 27.4, x₉ = 27.7, x₁₀ = 29.05, x₁₁ = 31.0, для которых назначены разные весовые нагрузки, зависящие от удаления индекса i от центра окна; для симметричной треугольной весовой функции они равны: wr5 = (0.077, 0.237, 0.387, 0.237, 0.077). Сглаженное значение y₉ составило (табл. 1, xwr5, рис. 8: 2):

y₉ = 0.077*26.99 + 0.237*27.44 + 0.387*27.67 + 0.237*29.04 + 0.077*29.54 = 28.45.

Несмотря на то, что соседние с центром значения x₈ = 27.44 и x₁₀ = 29.04 удалены от него на разное расстояние, 0.05 и 0.27, они получают одинаковые весовые нагрузки w₈ = w₁₀ = 0.237, поскольку, судя по индексам, являются одинаково близкими соседями к центральной точке окна.

 

Таблица 1. Расчет сглаженного значения y₉ в окне шириной h = 5 методом ближайшего соседа (xw5 и xwr5) и методом Парзена (xw)

	i	x	w5	xw5	wr5	xwr5	d	W	w	wx
536	7	26.99	0.20	5.40	0.08	2.08	0.14	0.73	0.22	5.88
537	8	27.44	0.20	5.49	0.24	6.50	0.05	0.91	0.27	7.44
538	9	27.67	0.20	5.53	0.39	10.71	0.00	1.00	0.30	8.27
541	10	29.04	0.20	5.81	0.24	6.88	0.27	0.45	0.14	3.95
542	11	29.54	0.20	5.91	0.08	2.27	0.37	0.25	0.08	2.24
Сумма			1	28.14	1	28.45		3.34	1	27.78

   

 

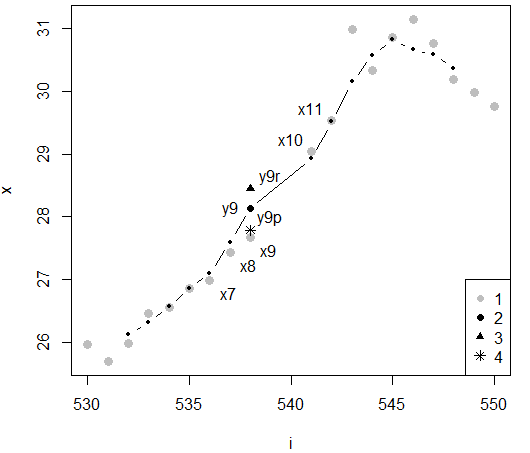
Рис. 8. Исходные (1) и сглаженные значения температуры тела гадюки (для точки 9) методом ближайшего соседа в прямоугольном (2, y9) и треугольном (3, y9r) окнах и методом Парзена (4, y9p) с треугольной весовой функцией; x7−x11 − 5 значений исходного ряда, взятых для расчета сглаженного значения y₉

Fig. 8. The initial (1) and smoothed values of the body temperature of the viper (for point 9) using the nearest neighbor method in rectangular (2, y9) and triangular (3, y9r) windows and the Parsen method (4, y9p) with a triangular weight function; x7−x11 − 5 values of the initial series taken to calculate the smoothed value of y₉

   

Назначения весовой функции методом Парзена

В отличие от предыдущего, метод Парзена учитывает фактическое расстояние между значениями x_i (Черненький, Птицын, 2005; Воронцов, 2009). Весовая функция рассчитывается в зависимости от расстояния между центром окна и всеми значениями x, попадающими в окно на данном шаге. Чем дальше от центра окна расположено значение x, тем меньше у него будет весовая нагрузка при расчете нового значения y. Рассмотрим эту технологию детальнее. Ширина окна h задается в единицах переменной x. В примере (табл. 1) пять соседних значений x₇ = 27.0, x₈ = 27.4, x₉ = 27.7, x₁₀ = 29.5, x₁₁ = 31.0 удалены от центральной точки (27.7) на разные расстояния: 0.7, 0.2, 0.0, -1.9, -3.3, новые веса должны быть им пропорциональны. Для унификации расчетов используют относительные расстояния, деля расстояния от центра на ширину окна: (x_i – x₀)/h. Например (табл. ОП, d), относительное расстояние от центра до точки i = 7 равно (при h = 5):

d₇ = (x₇ − x₉) / h = (26.99 −27.67) / 5 = 0.17.

При любой ширине окна относительное расстояние от центра как до левого, так и до правого края окна будет равно 0.5, так, для h = 5 d = |0 − 2.5| /5 = 0.5.

Можно задать, например, такую весовую функцию, чтобы весовая нагрузка была максимальной в центе и снижалась до 0 к краям, т. е. для d = 0, W = 1, а для d = 0.5, W = 0 (рис. 9). Иными словами, необходимо подобрать треугольную функцию зависимости W от d:

W = f(d) = K(|x_i – x₀|/h).

Указанному соотношению соответствует простое уравнение W = 1−2*d, используя которое можно рассчитать весовые нагрузки для всех значений x_i, входящих в окно (табл. ОП, W). Так, для второго значения x₈ = 27.44 расстояние составит:  |27.44 −27.67| / 5 = 0.05, а нагрузка W = 1−2*0.05 = 0.91.

 

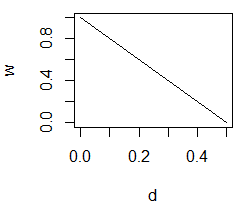
 Рис. 9. Правая ветвь треугольной весовой функции

Fig. 9. The right branch of the triangular weight function

 

Сумма всех нагрузок W оказалась больше единицы ΣW = 3.34. Однако в сумме весовые нагрузки в пределах окна должны составлять 1, значит, полученные веса надо нормировать на их сумму:

w = W/ΣW.

Получаем w₈ = W₈ /ΣW = 0.91 /3.34 = 0.27.

Итак, вклад значения x₈ в сглаженную величину y₉ составит:

w₈*x₈ = 0.27 * 27.44 = 7.4.

Суммирование вкладов всех объектов, включенных в окно, дает новое сглаженное значение y₉ = 27.78.

Все выполненные выше вычисления можно выразить следующими формулами:

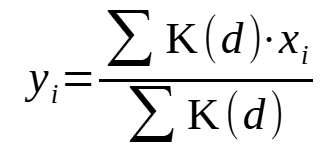 , где  .

Итак, для треугольной весовой функций имеем:

 . 

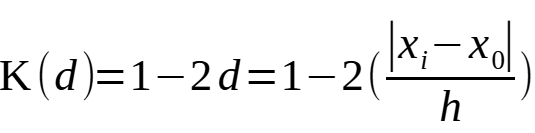head(ve<-read.csv("tve202280_5_10_46.csv"),2) i<-c(530:538,541:550) x<-ve[i,3] di<-c(7,8,9,10,11) w5=rep(0.2,5) ; xw5=w5*x[di] ; y5<-sum(xw5) wr5=c(0.077, 0.237, 0.387, 0.237, 0.077) ; xwr5=wr5*x[di] ; y5r<-sum(xwr5) d<-abs((x[9]-x[id])/5) ; pro<-a[1]+a[2]*d wp5<-round(pro/sum(pro),3) ; xwp5<-wp5*x[di] ; y5p<-sum(xwp5) (rez<-data.frame(i=i[id],x=x[id], w5,xw5,wr5,xwr5, d,pro,wp5,xwp5)) srez<-round(apply(rez,2,sum),2)

При рассмотрении результатов сглаживания средней треугольным окном ближайших соседей и треугольным окном Парзена хорошо видны различия (рис. 9). В первом случае сглаженное значение y₉ явно завышено, а в третьем − выглядят наиболее естественными.

Весовая функция Гаусса

Помимо прямоугольной и треугольной весовых функций при сглаживании широкой популярностью пользуется функция Гаусса:

.

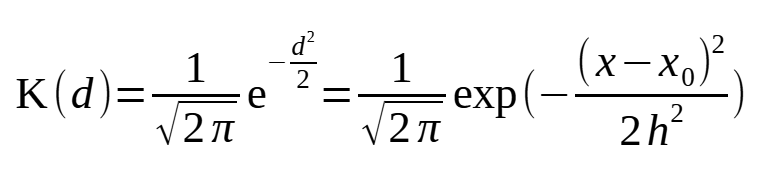У этой функции есть ряд преимуществ перед прочими функциями. Поскольку область определения этой функции составляет бесконечность, ±∞, для ее расчета не требуется отбирать значения x, соответствующие заданному окну, т. е. расчет функции можно выполнять по всем значениям ряда x. Величина h играет роль стандартного отклонения, значит, на расстоянии ±3h от точки сглаживания весовые нагрузки станут практически равны нулю, т. е. в активные расчеты вовлекаются значения из интервала примерно x_i ± 3h. Величину h можно назначить, исходя из соображений о нужной ширине окна сглаживания. Если для сглаживания температуры тела рептилии принять окно шириной 5 мин., то следует назначить h = 0.9, если огрублять данные до 60 мин., то h = 30. Расчеты с этими параметрами выполняет скрипт; результаты приведены на рис. 10.

head(ve<-read.csv("tve202280_5_10_46.csv"),2) i<-c(530:538,541:550) x<-round(ve[i,3],2) h d<-((x[9]-x)/h) pro<-(1/sqrt(2*pi))*exp(-(d^2)/2) (w<-round(pro/sum(pro),3)) (rez<-round(data.frame(i=i,x=x,d=d,W=pro,w=w,wx=w*x),3)) (y7<-sum(w*x))

 

 

 Рис. 10. Расчет весовой функции Гаусса для значения x₉ при ширине окна h = 0.9 и h = 30

Fig. 10. Calculation of the Gaussian weight function for the value x₉ at window widths h = 0.9 and h = 30

 

Весовые нагрузки узкого окна (h = 0.9) вовлекают в расчеты практически только ближайших соседей, отстоящих от центра на 3−4 шага. Широкое окно (h = 30) привлекает все окрестные точки. Для нашего короткого ряда (i = 1 ... 19) при h = 30 все веса оказались примерно одинаковы (они оценивают верхушку очень широкой гауссианы). Сглаживание с разными окнами дали разные значения y для точки 9: для окна h = 0.9 y₉ = ∑wx = 27.278, для h = 30 y₉ = ∑wx = 28.61.

 

Тренды

 Выявление трендов в общем смысле не является задачей сглаживания, это задача поиска зависимостей (регрессии) или анализа составных временного ряда (Шитиков, Мастицкий, 2017). Однако этот метод может служить для целей заполнения пробелов в данных. Для выявления генеральных трендов используются линейная регрессия, для выявления периодических составляющих − синусоиды, для выявления хода специфических зависимостей − криволинейные функции, в т. ч. степенные, экспоненциальные, логарифмические и полиномиальные. С помощью полиномов различных степеней можно достаточно точно охарактеризовать динамику изучаемого признака. Как известно, полином n−1-й степени может описать все n точек исходной выборки. Однако вычислять тренды, копирующие данные, нет никакого смысла, поскольку при сглаживании стоит задача избавления от изменчивости, а не ее точное описание. Имеет смысл аппроксимация с помощью какой-либо гладкой функции y_i = f(x_i). Однако необходимо помнить, что на конечный результат математического описания динамики какого-либо показателя накладывает отпечаток в большей мере форма той функции, которую предлагает теория, а не сами данные, которые наблюдаются в реальности.

В первом примере показано, что степенная функция зависимости массы тела от размера тела самцов гадюки позволяет выполнить интерполяцию для длины тела 25 см (11.4 г), для которой не было эмпирических данных (рис. 11).

head(ve<-read.csv("vip.csv" )) head(vm<-ve[ve$S=='m',]) head(ltp<-na.omit(vm[,10:11])) x<-ltp$LT ; y<-ltp$P tr<-lm(y~poly(x,2)) (new<-data.frame(x=seq(0,70,5))) ypr<-predict(tr,newdata=new) lt25<-data.frame(x=25) p25<-predict(tr,newdata=lt25) plot(ltp) lines(data.frame(new,ypr)) points(lt25,p25,pch=16) legend('topleft',legend=c(1,2),pch=c(1,16))

  

 Рис. 11. Зависимость массы (P) от длины тела (LT) самцов гадюки (1) и прогноз массы для особи (2) длиной 25 см с помощью полиномиальной регрессии

Fig. 11. The dependence of mass (P) on body length (LT) of male vipers (1) and the forecast of mass for an individual (2) with a length of 25 cm using polynomial regression

 

Во втором примере зависимость температуры тела рептилии от времени суток описана с помощью серии полиномов разных степеней (рис. 12). Полином второй степени выявляет генеральная составляющая повышения температуры утром и понижение днем вечером. А полином двадцатой степени смог выразить колебания изменения температуры тела в дневное время, связанное с облачной погодой (периодические прерывания инсоляции).

В среде R аппроксимацию можно выполнить с помощью функций lm() и glm(), включающих в себя функцию poly(), которая упрощает расчеты. Основными аргументами является зависимые и независимые переменные, формула вида функции, степень полинома. 

head(ve<-read.csv("tve202280_5_10_46.csv")) i<-seq(530,770) ; x<-ve[i,3] xpr2<-predict(lm(x~poly(i,2))) xpr20<-predict(lm(x~poly(i,20))) plot(i,x,cex=1.2,pch=16,col='grey',type='l',lwd=4) lines(data.frame(i,xpr2),lwd=3,lty=2) lines(data.frame(i,xpr20),lwd=3) legend('bottomright',legend=c(1,2,3),lty=c(1,2,1), col=c('grey',1,1),lwd=c(4,2,2))

  

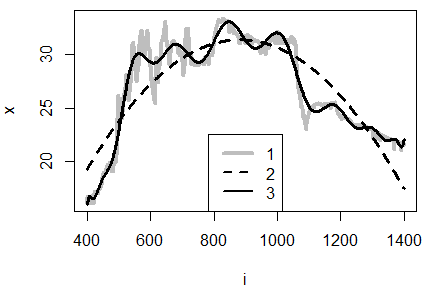
 Рис. 12. Данные по температуре тела гадюки (1), сглаженные полиномами второго (2) и двадцатого (3) порядка; по оси абсцисс — минуты от полуночи

Fig. 12. Data on the body temperature of the viper (1), smoothed by polynomials of the second (2) and twentieth (3) order; on the axis of the abscissa — minutes from midnight

 

Выявленный тренд (уравнение) позволяет рассчитать недостающее значение y_i  в пару к имеющемуся значению x_i, что и составляет метод заполнения по регрессии (Литтл, Рубин, 1990). Предсказания будут более обоснованными, если для восстановления пропуска использовать уравнения множественной регрессии с несколькими исходными переменными, не ограничиваясь линейными моделями, но добавляя и нелинейные члены.

 

 Имитационное моделирование

Сгладить динамики равномерного процесса (и выполнить интерполяции) можно методом имитационного моделирования (Коросов, 2002, 2024). Имитационная модель призвана описывать зависимости переменных и процессы, длящиеся во времени и простирающиеся в пространстве. Жизнь модели превращается в серию шагов, которые перебираются в цикле от первого до последнего. На каждом шаге рассчитывается новое значение y’, используя приращение dy’, которое было получено на предыдущем шаге:

dy_i = f(a, x_i, my_i),

my(i+1) = my_i+ dy_i,

где dmy_i – приращение значения модели на i-м шаге,

a – коэффициенты пропорциональности,

x_i – значения независимых переменных (внешней среды),

my_i – значение модели на i-м шаге,

my(i+1) – значение модели на следующем i+1-м шаге.

Первое уравнение рассчитывает приращение модели, второе – новое значение модели. Зачастую представляет интерес автономный процесс, когда текущее приращение модели зависит от текущего модельного значения (здесь – линейно):

dy_i = a1 + a2*my_i.

В расчете dy_i могут участвовать и внешние факторы (x_i), имеющие разную выраженность на разных шагах модели (в разные моменты времени):

dy_i= a1 + a2*my_i + a3*x_i.

Чтобы модель хорошо описывала фактические данные, необходимо ее настроить, т. е. подобрать оптимальные коэффициенты a. С помощью функции минимизации nlm() или optim() приходится подбирать такие коэффициенты a, чтобы минимизировать невязку, свести к нулю сумму квадратов отклонения модельных значений от эмпирических: Σ (y – my)² → 0.

Важно отметить, что модель с одними и теми же коэффициентами a рассчитывает значения y на каждом шаге, следовательно, шаги должны быть равномерными, одинаковой длительности или длины. Проще всего заранее подобрать множество шагов (ось абсцисс) таким образом, чтобы они начиналась с единицы i₁ = 1 и прирастали тоже на 1, т. е. были рядом натуральных чисел: i = 1, 2, 3 ... m.

Для имитации увеличения массы самцов гадюки (p) по мере увеличения длины тела (lt) в качестве шага выбрали прирост на 1 см: i₁ = 1 см, i₂ = 2 см ... i₆₀ = 60 см, ns = 60.

#============== model ============= yymod<-function(a){ yy[1]<-a[3] for (i in 1:(ns-1)) ;{dy yy[i+1] #============= minimizing ========== minres<-function(p) {yy<-yymod(p) return(sum((y-yy[x])^2,na.rm=TRUE))} #-------------- read data ------------------------ head(data<-read.csv("vip.csv" )) head(vm<-data[data$S=='m',]) head(xy<-na.omit(vm[,10:11])) (N<-nrow(xy)) ; n (x<-c(1,xy$LT[r])) ; (y<-c(1,xy$P[r])) #----------------- modeling ---------------------- ns<-60; s p<-c(1,0.01,0) (mod<-nlm(minres,p)) a<-mod$estimate (p<-a) #------------------ plot result model ------------ yy<-yymod(p) plot(x,y,xlim=c(1,60),ylim=c(1,130)) lines(s,yy,lwd=2,col=3) points(25,yy[25],pch=16)

В первом блоке задана функция расчета модельных значений y, причем первое значение теоретического ряда yy рассматривается как настраиваемый параметр. Во втором блоке задана функция расчета невязки − суммы квадратов отличия модели от реальности. В третьем блоке прочитаны данные и подготовлены для манипуляции; в эмпирические ряды добавлена пара значений p = 1 и lt = 1 для стабилизации хода модельной кривой. В следующем блоке задана структура модели − 60 шагов по 1 см, массив под расчетные значения, приблизительные модельные параметры p; выполнена настройка модели. В последнем блоке рассчитаны модельные значения и построена диаграмма (рис. 13); у гадюки с длиной тела 25 см прогнозная масса − 15.7 г. В целом эта модель отличается от полиномиальной тем, что не требует аргумента x.

  

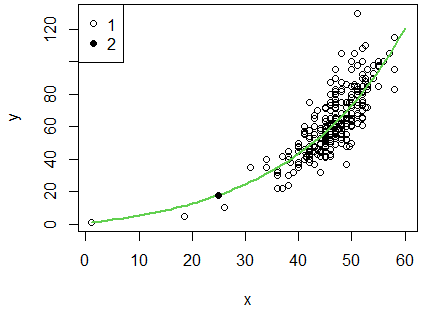 Рис. 13. Имитация зависимости массы (P) от длины тела (LT) самцов гадюки (1) и прогноз массы (2) для особи длиной 25 см

Fig. 13. Simulation of the dependence of mass (P) on body length (LT) of male vipers (1) and the forecast of mass (2) for an individual with a length of 25 cm

 

 Локальная регрессия

Этот метод аппроксимации данных не обременяет результаты теоретическими соображениями и обладает высокой степенью гибкости. Метод во многом похож на фильтр. В его основу так же положено скользящее окно определенного размера.

Отличие состоит в том, что в каждом окне рассчитывается не взвешенная средняя по соседним точкам, а точечный прогноз по локальной линии регрессии, построенной по точкам, попавшим в окно. Прогнозное значение приписывается центру окна (рис. 14).  Поскольку регрессия аппроксимирует каждое из значений ряда, результирующая кривая оказывается плавной. При этом участие каждой точки в расчете линии регрессии зависит от расстояния до центра окна, т. е. используется парзеновское окно.

  

 

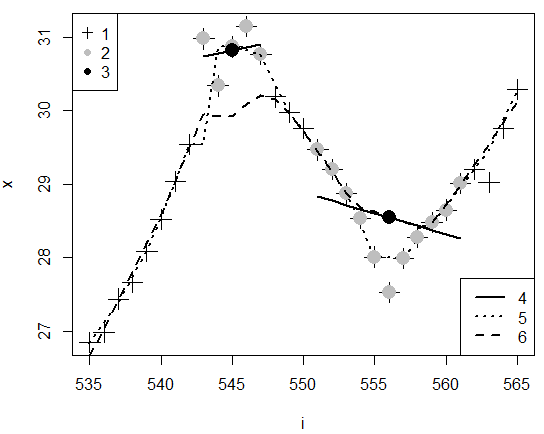
Рис. 14. Поминутная динамика температуры тела гадюки и расчет сглаженных значений y₅₄₅ в окне размером h = 5 и y₅₅₆ в окне размером h = 11: 1 − исходные значения x, 2 − значения, попавшие в окно h = 5 в окрестностях точки x₅₄₅ и в окно h = 11 в окрестностях точки x₅₅₆, 3 − точки y₅₄₅ и y₅₅₆, рассчитанные по регрессии, 4 − линии регрессии по 5 и по 11 точкам, 5 − линия от функции lowess() с окном h = 5 (f = 5/31 = 0.16), 6 − линия от функции lowess() с окном h = 11 (f = 11/31 = 0.34)

Fig. 14. Minute-by-minute dynamics of the viper's body temperature and calculation of smoothed values of y₅₄₅ in a window of size h=5 and y₅₅₆ in a window of size h = 11: 1 − initial values of x, 2 − values that fell into the window h = 5 in the vicinity of point x₅₄₅ and into the window h = 11 in the vicinity of point x₅₅₆, 3 are points y₅₄₅ and y₅₅₆ calculated from regression, 4 are regression lines for 5 and 11 points, 5 is a line from the lowess() function with a window of h = 5 (f = 5/31 = 0.16), 6 is a line from the lowess() function with a window of h = 11 (f = 11/31 = 0.34)

 

В среде R для такого сглаживания одной переменной x удобно пользоваться функцией lowess(x,f) с двумя аргументами: x − вектор для сглаживания, f − ширина окна, отнесенная к длине ряда f = h/n. Функция сразу возвращает сглаженное значение, готовое к нанесению на диаграммы. Название lowess − это акроним от local weited regression.

Для построения поверхности, когда одновременно аппроксимируется две или несколько входных переменных, используется функция loess() (хотя она может сглаживать и один ряд). Подбор коэффициентов для локальной регрессии (линейной или полиномиальной) осуществляется либо методом наименьших квадратов, либо с помощью алгоритмов подгонки − минимизации суммы квадратов отклонений (Chambers et al., 2018; Difference…, 2018).

На рис. 14 видно, что значения, спрогнозированные нами напрямую по линии локальной регрессии, практически совпадают со значениями, предсказанными функцией lowess. Отличие связано с тем, что при расчете нашей (иллюстративной) регрессии поправка на расстояние от центра окна не вводилась.

head(ve<-read.csv("tve202280_5_10_46.csv")) i<-c(535:565) ; x<-round(ve[i,3],2) di<-c(9:13) ; h<-length(di) dh<-h/length(i) ; (ce<-1+(h-1)/2) reg<-lm(x[di]~i[di]) ;(xx<-predict(reg)) spx<-lowess(x,f = dh) ilx<-data.frame(i,spx)[,c(1,3)] plot(i,x,cex=2,pch=3) points(i[di],x[di],cex=2,pch=16,) points(i[di[ce]],xx[ce],cex=2,pch=16) lines(i[di],xx,lwd=2) lines(ilx,col=1,lty=3,lwd=2) legend('topleft',legend=c(1,2,3),pch=c(3,16,16),col=c(1,'grey',1)) legend('bottomright',legend=c(4,5,6),lty=c(1,3,2),lwd=c(2,2,2))

 Как и для линейного фильтра, чем шире выбрано окно для локальной регрессии, тем более плавной становится сглаженная линия, чем окно уже, тем подробнее отображаются перепады значений признака x.

 

 Сплайн

Сплайн представляет собой кривую, «сшитую» «встык» из нескольких кривых полинома 2-3 порядка (рис. 15).

 

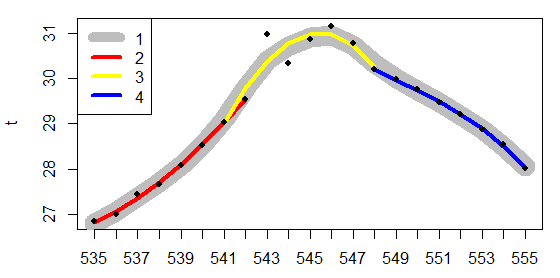
 Рис. 15. Сглаживание исходных данных по температуре тела гадюки с помощью сплайна (1) и трех кривых кубического полинома для трех участков по 8 точек (2-4)

Fig. 15. Smoothing of the initial data on the viper body temperature using a spline (1) and three cubic polynomial curves for three sections of 8 points (2-4)

 

В среде R сплайн строится с помощью функции smooth.spline(t,spar) с двумя основными аргументами — именем исходного ряда данных (x) и базовой длиной отрезка (шириной окна) для которого строится локальная полиномиальная кривая (spar). Чем больше величина spar, тем более плавной будет сглаженная кривая. Серьезную техническую проблему представляет «сшивка» каждой пары кривых. Однако этот вопрос выходит за рамки нашей темы, поэтому остается только ограничиться иллюстрацией того факта, что три полиномиальных кривых длиной по 8 точек (spar=8/21=0.38) вполне точно ложатся на кривую сплайна. 

head(ve<-read.csv("tve202280_5_10_46.csv")) d<-c(535:555) ; t<-round(ve[d,3],2) ; i<-1:length(d) spx<-lowess(t,f = 0.38) plot(i,t,cex=2,pch=3,type='n',xaxt='n') spx2<-smooth.spline(t,spar=0.38) lines(spx2,lwd=20,col='grey') a=1:8 ; b=7:14 ; c=14:21 is<-data.frame(a,b,c) ; xs<-data.frame(t[a],t[b],t[c]) y<-xs[,1] ; x<-is[,1] lines(x,predict(lm(y~poly(x,3))),lwd=4,col='red') y<-xs[,2] ; x<-is[,2] lines(x,predict(lm(y~poly(x,3))),lwd=4,col='yellow') y<-xs[,3] ; x<-is[,3] lines(x,predict(lm(y~poly(x,3))),lwd=4,col='blue') points(i,t,cex=.8,pch=16) legend('topleft',legend=c(1,2,3,4),lwd=c(10,4,4,4), col=c('grey','red','yellow','blue')) axis(1,at=i,d)

 Разрывающие фильтры

Помимо фильтров, сглаживающих изменчивость, предложены разнообразные фильтры, подчеркивающие аномальную изменчивость, существенные перепады значений. Это разностные, разрывающие, контрастоповышающие, дифференцирующие, повышающие резкость и др. фильтры (Дэвис, 1990; Гонсалес и др., 2005, 2012; Иванов и др., 2007; Яне, 2007). Основная идея состоит в том, что первая и вторая производные от изучаемой функции (ряда) x будут резко меняться в местах перепада значений x. Соответственно, их графики и выскакивающие значения позволяют судить о нарушении плавной динамики показателя, о наличии границы между областями, перегиба на графике относительно спокойного изменения переменной x. Разрывающие фильтры включают в свои формулы аналоги первой и второй производных.

Мы рассмотрим только один из таких фильтров − расщепляющее окно. Этот фильтр составлен из двух частей, левой (л) и правой (п) относительно центральной точки, которой приписывается отфильтрованное значение. В формуле сравниваются две половинки окна и их количественные показатели − средняя (М) и дисперсия (S²):

.

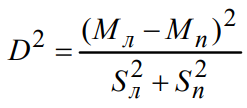При оценке параметров центр окна x_i входит и в левую, и в правую выборки.

Полученная метрика будет иметь минимальное значение, когда разность между средними отсутствует, а дисперсии велики; это соседние точки на вершинах и на дне впадин. Величина D отыскивает положение экстремумов.

При анализе суточного хода температуры тела гадюки (рис. 16), большой интерес представляют ее резкие перепады, свидетельствующие либо об изменении потока инсоляции в тени облаков, либо о терморегуляторной реакции, меняющей текущую температуру тела. Провалы, обнаруженные разрывающим окном, четко соответствуют точкам перелома хода кривой.

   

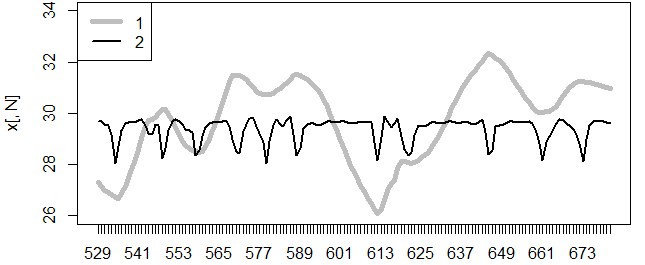
Рис. 16. Поминутный ход дневной температуры тела гадюки (1) и динамика показателя перегиба разрывающего окна (2) с шириной окна h=7

Fig. 16. The minute-by-minute course of the daily body temperature of the viper (1) and the dynamics of the inflection index of the bursting window (2) with a window width of h=7 

head(ve<-read.csv("tve202280_5_10_46.csv")) i<-c(535:565) ; x<-round(ve[i,3],2) di<-c(9:13) ; h<-length(di) dh<-h/length(i) ; (ce<-1+(h-1)/2) head(ve<-read.csv("tve202280_5_10_46.csv")) di<-c(525:685) ; te<-ve[di,3] n<-length(di) h t<-lowess(te,f = .08)$y j<-seq(1,m) ; x<-t[j] for (i in 1:(h-1)){x<-data.frame(x,t[j+i])} M<-abs(apply(x[,1:N],1,mean)-apply(x[,N:h],1,mean))^2 S<-apply(x[,1:N],1,sd)^2+apply(x[,N:h],1,sd)^2 (msc<-data.frame(M,S,c=round(sqrt(M/S),2))) plot(x[,N],ylim=c(26,34),type='l',col='grey',lwd=5,xaxt='n') lines(msc[,3]+28,lty=1,lwd=2) axis(1,at=j,di[j+N]) legend('topleft',legend=c(1,2),lwd=c(5,2),col=c('grey',1))

 

 Главные компоненты

Компонентный анализ предназначен для выявлении структуры отношений многомерных данных, вычленяя группы зависимых признаков и группы сходных объектов. Этим методом обрабатывают двумерные таблицы, в которых столбцы имеют смысл отдельных переменных, а строки относятся к отдельным объектам. На основе этих исходных характеристик он рассчитывает линейные индексы (главные компоненты), коэффициенты в которых показывают, насколько сильно исходные признаки коррелируют друг с другом. Расчетные значения главных компонент выражают некие общие причины, из-за которых группы признаков изменяются согласованно, а объекты оказываются разделенными на группы по силе сходства (Дэвис, 1990).

Один из вариантов применение компонентного анализа − изучение последовательностей, временных рядов, для выявления доминирующих трендов и периодических составляющих (Ефимов и др., 1988). С целью формирования из одного временного ряда двумерного массива используется принцип скользящего окна — последовательно со смещение на 1 шаг выбирают серию из h соседних значений (h – ширина окна, или лаг), из которых формируют таблицу исходных значений.

Рассматривая данные по суточной динамике температуры рептилии (рис. 17), можно заметить, столбцы таблицы составлены из фрагментов исходного ряда («tve202280_5_10_46.csv»), смещенных относительно друг друга. Все расчеты описаны в скрипте «script 01 PCA as filter.R». 

  

Рис. 17. Фрагмент временного ряда (te, n = 288; замеры взяты через 20 мин. для 4 суток) и фрагмент массива (xt, 11*277), составленного из отрезков по h = 11 значений 

Fig. 17. Fragment of the time series (te, n = 288; measurements were taken after 20 min. for 4 days) and a fragment of an array (xt, 11*277) made up of segments of h = 11 values

 

При исследовании временных трендов предполагается, что каждое значение временного ряда в каком-то смысле определяется серией предыдущих значений. «Нарезая» ряд на фрагменты, в центр внимания мы помещаем такую связанную совокупность соседних значений (Коросов, 1996). В примере массив составлен из 11 соседних значений, формирующих 11 столбцов. Они играют роль отдельных переменных, между которыми отыскиваются корреляции и для которых подбираются коэффициенты пропорциональности в главных компонентах, факторные нагрузки (они же весовые коэффициенты). Каждый столбец относительно другого представляет собой показатель «температура в близкий момент времени». Коэффициенты парной корреляции между такими столбцами имеют смысл автокорреляции и свидетельствуют о силе зависимости температуры в момент i от температуры в предыдущие моменты i−1, i−2, i−3, …. Факторные нагрузки концентрируют информацию обо всех взаимных корреляциях. Факторные нагрузки, соответствующие одной компоненте, по сути представляют собой автокорреляционную функцию по длине, равной ширине окна; в терминах сглаживания факторные нагрузки одной компоненты − это весовая функция, ядро. Поскольку динамика автокорреляций на разных фрагментах может быть разной, компонентный анализ рассчитывает несколько главных компонент, несколько наборов факторных нагрузок (несколько наиболее характерных для данного ряда автокорреляционных функций). При этом выполняются условие ортогональности компонент и условие снижения дисперсий главных компонент.

Решить, какие компоненты имеют смысл, помогает анализ величины их дисперсий (рис. 18. m.e$values). Поскольку исходные значения нормированы и центрированы, средняя дисперсия одного признака равна 1, а полная дисперсия комплекса равна числу изучаемых переменных, в примере − 11. В нашем случае только первые две дисперсии больше единицы, а последующие − меньше единицы, что меньше дисперсии отдельной исходной переменной, значит, ими можно пренебречь. Итак, только первые две компоненты могут быть интересны, прочие в основном отражают стохастический шум.

 

  

Рис. 18. Значения дисперсий (m.e$values) и факторные нагрузки (m.a$vectors) первых пяти компонент (окно h = 11)

Fig. 18. Variance values (m.e$values) and factor loadings (m.a$vectors) of the first five components (window h = 11)

 

Как правило, факторные нагрузки первой компоненты представлены почти равными значениями, что соответствует плоскому фильтру (или прямоугольному ядру), фактически это простая скользящая средняя, включающая в расчет h соседних значений с почти равными весами (см. рис. 18). Соответственно, график первой главной компоненты представляет собой сглаженную общую динамику изучаемого показателя (рис. 19). Отметим, что в качестве исходных данных взят ряд из центра окна (xt[,6]). Чем шире окно, тем более плавным будет график компоненты (рис. 20).

 

 

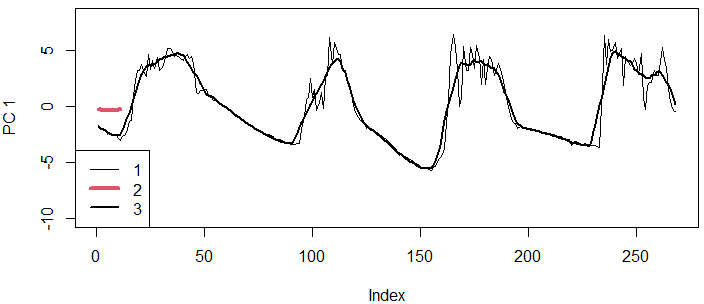
Рис. 19. Сглаживание с помощью первой главной компоненты (окно h = 11); 1 − исходные шкалированные данные (st[,6]*3.2), 2 − форма фильтра PC1 (график факторных нагрузок первой компоненты, m.e$values[,1]), 3 − значения первой главной компоненты

Fig. 19. Smoothing using the first main component (window h = 11); 1 is the original scaled data (st[,6]*3.2), 2 is the form of the PC1 filter (graph of factor loads of the first component, m.e$values[,1]), 3 is the values of the first main component

 

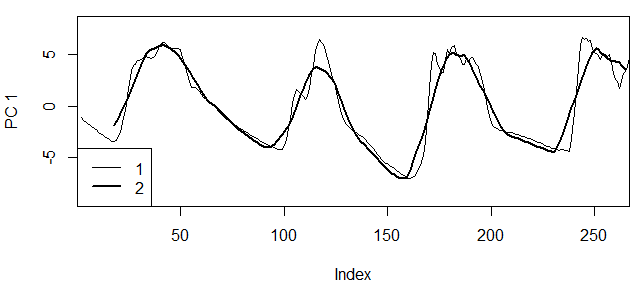
Рис. 20. Графики первой главной компоненты: 1 — окно h = 5, 2 — окно h = 21

Fig. 20. Graphs of the first main component: 1 — window h = 5, 2 — window h = 21

 

Факторные нагрузки второй компоненты представляют собой набор значений, по форме похожий на какой-либо другой типичный фрагмент исходного ряда. В нашем случае это левый склон круто восходящей волны: первые значения коэффициентов большие отрицательные, последние − большие положительные (см. рис. 18, m.e$vectors[,2]). Расчетные значения второй главной компоненты будут тем выше, чем точнее изучаемый фрагмент по форме соответствует этим факторным нагрузкам. Так, начальные значения температур показывают плавное снижение, что плохо соответствует нагрузкам во второй компоненте, следовательно, значения второй компоненты оказались довольно низкими (около нуля). Начиная с 15-го отсчета график температур начал подниматься, стал больше соответствовать «волне» второго набора нагрузок, вследствие чего значения второй компоненты стали возрастать и достигли пика примерно на 20-м отсчете (рис. 21). Затем начался период переменчивой температуры, что привело к падению величины второй компоненты. К концу первого дня (40−45-й отсчет) температура стала резко падать, что прямо противоположно графику нагрузок-2, поэтому значения второй компоненты оказались большими отрицательными. На протяжении последующих дней наибольшая скорость прироста температуры хорошо отражается максимальными пиками второй компоненты, наибольшая скорость падения − резкими провалами (см. рис. 21).

На основании этих описаний первую компоненты можно назвать «средняя взвешенная температура», вторую − «скорость роста температуры».

 

  

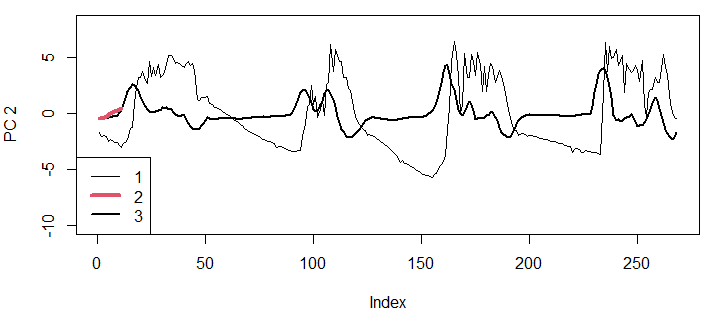
Рис. 21. Сглаживание с помощью второй главной компоненты (окно h = 11); 1 − исходные шкалированные данные (st[,7]*3.2), 2 − форма фильтра PC2 (график факторных нагрузок второй компоненты, m.e$values[,2]), 3 − значения второй главной компоненты

Fig. 21. Smoothing by using the second main component (window h = 11); 1 − initial scaled data (st[,7]*3.2), 2 − the form of the PC2 filter (graph of factor loads of the second component, m.e$values[,2]), 3 − values of the second main component

 

В отличие от других вариантов фильтрации, форма фильтра в компонентном анализе задается не произвольно, но исходя из автокорреляционных зависимостей между соседними значениями, т. е. исходя из структуры корреляций. В каком-то смысле это «естественные» корреляционные фильтры.

Продолжая тему анализа временного ряда, необходимо отметить, что и спектральный анализ (поиск периодических компонент ряда) также рассматривается как вариант линейной фильтрации, когда в качестве фильтров берутся отрезки гармоник (Ефимов и др., 1988).

К числу многомерных методов, которые используют скользящее окно для целенаправленного видоизменения рядов данных, можно отнести методы, применяющие не метрику корреляций между фрагментами ряда, а метрики евклидовых расстояний, в т. ч. и между нечисловыми показателями (например, по числу совпадений). В таком случае для сглаживания можно использовать неметрическое шкалирование и модификацию метода главных компонент − PCA-seq (Efimov et al., 2019).

Оригинальные методы исследований

В центре теории ядерных методов находится понятие ядра. Динамические иллюстрации смысла ядерных методов можно увидеть на сайте (Kernel…, 2023).

 Ядро

Ядро − это набор коэффициентов, с помощью которых значения x, попадающие в окно, преобразуются в единственное значение y_i. Ядерная функция − это математический метод расчета весовых коэффициентов в ядре (Воронцов, 2007). Ядро, скользящее вдоль ряда значений x, превращает его в ряд сглаженных значений y. В нашем первом примере (см. рис. 5) коэффициенты 0.33, 0.33, 0.33, служащие для расчета скользящей средней по тройкам, это и есть ядро. Можно выразиться и по-другому: ядро − это вторая функция w, которая в процессе свертки превращает функцию x в функцию y. В приведенных выше примерах ядра строились методом ближайших соседей.

В методах оценки ядерных плотностей распределения и ядерной регрессии используется Парзеновское окно. Весовые коэффициенты этого окна назначаются пропорционально расстоянию d значений x от центра окна x_i. Для характеристики размера ядра (фильтра) используются разные термины: ширина окна, лаг, ширина ядра, диаметр ядра, полоса фильтрации, полоса пропускания. По сути все они обозначают ширину окна, которое скользит вдоль по ряду значений x и с помощью той или иной ядерной функции превращает группу видимых значений x в сглаженные значений y.

Ядерные функции могут быть различными, т. е. способы расчета весовых коэффициентов могут различаться (Норкин, 2024). В прямоугольном ядре весовые коэффициенты одинаковы для всех значений, попавших в окно. В треугольном ядре веса снижаются от центра к периферии прямо пропорционально расстоянию, гауссова ядерная функция задает плавное снижение весов. Предложены ядра и с другими свойствами, которые специально задаются в аргументах соответствующих функций среды R ("rectangular", "triangular", "epanechnikov", "biweight", "gaussian", "cosine", "optcosine") (рис. 22).

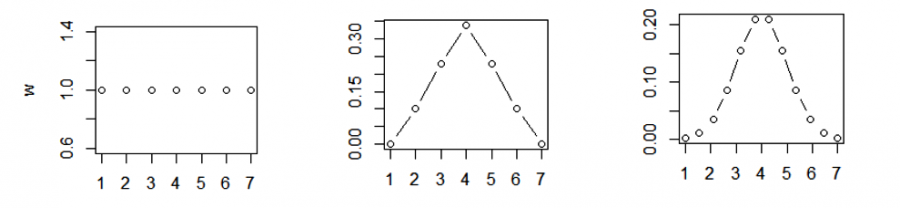
Рис. 22. Виды ядерных весовых функций: А — прямоугольная, Б — треугольная, В — Гаусса

Fig. 22. Types of nuclear weight functions: A — rectangular, B — triangular, C - Gaussian

 

 Ядерная регрессия

Ядерная регрессия, или ядерное сглаживание, служит для общей характеристики зависимости одной переменной (в примере – температура, x) от другой (в примере — минуты суток, i). Технология процесса ядерного сглаживания в общем рассмотрена выше (см. Весовая функция Гаусса). Вначале выбирается ширина окна h и вид ядерной функции K для назначения весовых коэффициентов w для точек x, попавших в окно (в зависимости от их расстояния d до центра). Ядро (окно) скользит вдоль ряда i, поочередно выделяя группы значений x, назначая им весовые коэффициенты w, рассчитывая произведения wx и их сумму, которая и оказывается значением y_i, относящимся к центру окна (Воронцов, 2007; Кэмерон, Триведи, 2015).

В среде R сглаживание выполняется с помощью функции ksmooth(), основные аргументы − это массив данных для сглаживания (x,y), принятая ядерная функция (kernel) и ширина окна (bandwidth − полоса пропускания) в единицах оси абсцисс (x). Аргумент kernel устанавливает весовую функцию или прямоугольную (расчет средних), или гауссиану и др. На рис. 23 представлены результаты сглаживания с помощью узкого h = 5 и широкого h = 50 окон и гауссианы как весовой функции.

  

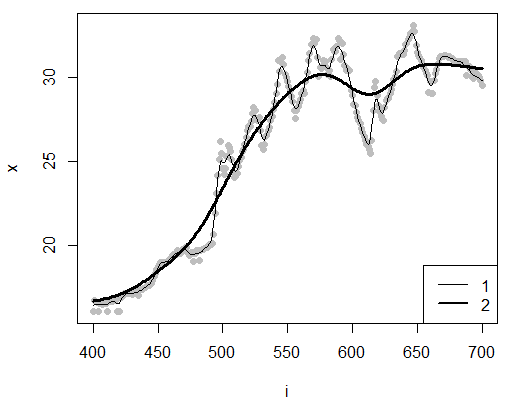
Рис. 23. Сглаживание динамик суточной температуры тела гадюки (6−16 часов) с помощью ядерной регрессии для окон размером h = 5 (1) и h = 50 (2) (ядерная функция − гауссиана)

Fig. 23. Smoothing the dynamics of the daily body temperature of a viper (6−16 hours) using nuclear regression for windows of size h = 5 (1) and h = 50 (2) (Gaussian nuclear function)

head(ve<-read.csv("tve202280_5_10_46.csv")) i<-seq(400,700) ; x<-ve[i,3] y5 <-ksmooth(i,x,kernel = "normal",bandwidth = 5) y50<-ksmooth(i,x,kernel = "normal",bandwidth = 50) plot(i,x,pch=16,col='grey') lines(y5) lines(y50,lwd=3) legend('bottomright',legend=c(1,2),lwd=c(1,2))

Предложены и другие технологии расчета ядерной регрессии, например, пакет {np} среды R позволяет глубже анализировать ядерную регрессию, в частности рассчитывать доверительные интервалы (Nonparametric…, 2024).

  

Ядерное сглаживание распределений

Исходная совокупность для сглаживания распределений представляет собой наборы значений x, как близкие друг к другу (сконцентрированные в одних областях оси x), так и взаимно удаленные (разреженные группы). Сглаживанию подлежат не значения x, а частота повторений или «сгущений» значений x. В процессе расчетов формируется ряд новых относительных частот p_j, новое распределение.

В среде R ядерную оценку плотности распределения выполняет функция density(). Внешне ее работу можно представить следующим образом (рис. 24):

plot(density(x=c(1,2,2.3),bw=.4))

Вокруг каждого исходного значения x_j (в примере их всего три) строятся «ядра» − отдельные «искусственные» распределения (в примере − нормальные). Затем все ядра объединяются, т. е. суммируются их относительные частоты; результирующее распределение и является искомой сглаженной оценкой плотности (Everitt, Hothorn, 2011).

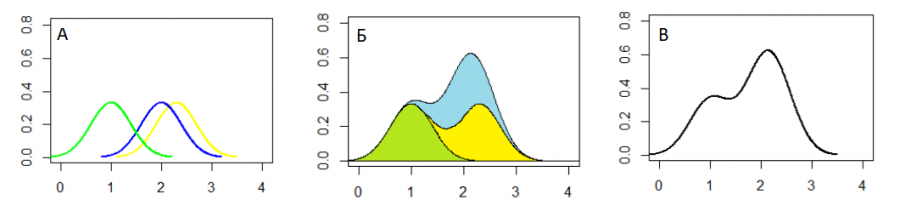 Рис. 24. Этапы построения оценки плотности распределения для x<-c(1,2,2.3): А − построение ядер, Б − объединение ядер, В − результирующая плотность распределения

Fig. 24. The stages of constructing a distribution density estimate for x<-c(1,2,2.3): A − building the, Б − combining the kernels, В −  the resulting distribution density

 

Привычная форма представления распределения − это гистограмма, для построения которой ось x разбивается на серию равновеликих интервалов, в которых подсчитывается число значений x, попавших в пределы каждого интервала a_j. К сожалению, форма гистограммы существенно меняется в зависимости от ширины выбранного интервала и положения первого отсчета x_min. Ядерная оценка призвана, во-первых, сделать гистограмму независимой от ширины интервала, во-вторых, дополнить случайные провалы в контуре распределения.

Процедура ядерной оценки плотности аналогична ядерному сглаживанию, рассмотренному выше, но отличается в деталях. Рассмотрим конкретный пример применения функции density() с аргументами x, bw, kernel, n.

Выборка значений x − это данность, независимая от процедуры сглаживания. Однако расчеты ядерной плотности не обязательно выполнять по всей выборке; используя процедуры ресамплинга, можно лучше изучить статистические свойства выборки (Мастицкий, Шитиков, 2014).

При выборе функции ядра обычно рекомендуют гауссиану,  kernel="gaussian". Форма распределения Гаусса зависит от величины стандартного отклонения, S.

Задавая ширину окна bw (bandwidth, пропускную полосу), ориентируются как раз на величину стандартного отклонения, рассчитанного для исходного ряда x. Обычно рекомендуют "nrd0". Эта эмпирическая величина составляет примерно 40 % от S и зависит от характеристик ряда x (подробнее см. ?bw.nrd0). Ширину ядра можно задавать и числом. Как и в других методах сглаживания, ширина окна определяет степень сглаживания; при очень узком окне сглаженная кривая скопирует гистограмму, при очень широком − новое распределение станет равномерным.

Аргумент n − это количество равноотстоящих точек, для которых необходимо оценить плотность. По умолчанию n = 512. В примере (см. рис. 24) именно поэтому вокруг каждого значения и построена гладкая кривая плотности, что использовалось большое число значений для расчета плотности нормального распределения.

Рассмотрим расчет функцией density() пяти значений плотности (n=5) вокруг отдельного значения (x=2), с окном, равным единице (bw=1).

> str(density(x=2,bw=1,kernel="gaussian",n=5)) List of 7 $ x : num [1:5] -1 0.5 2 3.5 5 $ y : num [1:5] 0.00447 0.12983 0.39887 0.12983 0.00447 $ bw : num 1 $ n : int 1 $ call : language density.default(x = 2, bw = 1, n = 5) $ data.name: chr "2" $ has.na : logi FALSE - attr(*, "class")= chr "density" > dnorm(x=c(-1,0.5,2,3.5,5),mean=2, sd=1) [1] 0.004431848 0.129517596 0.398942280 0.129517596 0.004431848

 Как можно видеть, используя заданные аргументы, функция density(), во-первых, создает окно размером от x±3*bw – от −1 до 5. Во-вторых назначает пять (n=5) равноотстоящие значения $x для расчета относительных частот: $x = −1, 0.5, 2, 3.5, 5. В-третьих, рассчитывает значения плотности нормального распределения $y = 0.00447, 0.12983, 0.39887, 0.12983, 0.00447. Эти значения практически совпадают с расчетами по функции dnorm() для тех же пяти значений x, средней mean=2 и стандартным отклонением sd=1.

На этом примере отчетливо видно различие между терминами «ядерная функция» и «ядро». Первое — это метод расчета относительных частот распределения ("gaussian"). Второе — это конкретные значения рассчитанных относительных частот (0.00447, 0.12983, 0.39887, 0.12983, 0.00447), привязанных к определенным позициям на шкале x (−1, 0.5, 2, 3.5, 5).

Полная процедура оценки ядерной плотности для выборки значений x выглядит следующим образом. Окно движется вдоль ряда х, принимая очередное выборочное значение x_i за центр нового распределения. Затем рассчитывает диапазон значений x (x±3*bw) для расчета новых частот, задает для этого интервала серию равномерно отстоящих значений x и рассчитывает для них теоретически значения нормальной плотности. Далее сохраняет результаты и выполняет аналогичные расчеты для следующего значения x_i+1. После расчета всех оценок плотности для всех значений x выполняется их объединение относительных частот в общее распределение y.

Чем шире окно, тем шире будут ядра, тем более гладкой будет результирующая кривая распределения, чем уже окно, тем ближе будет график плотности к исходной гистограмме (рис. 25).

head(data<-read.csv("vip.csv" )) head(vm<-data[data$S=='f',]) head(xy<-na.omit(vm[,10:11])) N<-nrow(xy) ; n x<-c(1,xy$P[r]) p<-hist(x,breaks=50,plot=FALSE) plot(p$mids,p$density,type='h',lwd=5,col='grey',xlab='p, г') lines(density(x,bw=3),lwd=1) lines(density(x,bw='nrd0'),lty=2,lwd=2) legend('topleft',legend=c(1,2,3),lty=c(1,1,2),lwd=c(5,1,2),col=c('grey',1,1))

 

  

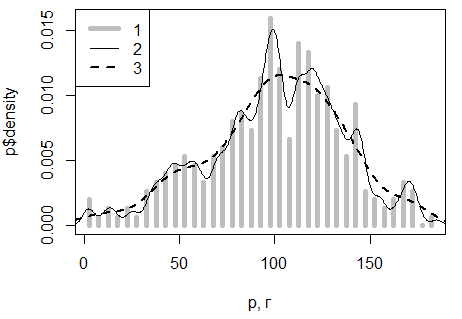
Рис. 25. Гистограмма (1) и ядерные оценки плотности распределения массы обыкновенной гадюки (p, г) с окнами шириной bw=3 (2) и (3)

Fig. 25. Histogram (1) and nuclear estimates of the mass distribution density of the common viper (p, g) with windows of width bw=3 (2) and (3)

Обсуждение

Выбор метода сглаживания в конце концов определяется тем, с какой целью производится это сглаживание. Для интерполяции по точкам с неизвестными данными лучше подойдут регрессии, ядерные методы; для иллюстраций трендов − сплайны и полиномы и пр.

В любом случае потребуется провести кривую так, чтобы она в наименьшей степени зависела от случайных ошибок, т. е. избавлялась от «излишней» изменчивости и выявляла «основные» тренды. Если эти категории («лишний», «основной»), апеллирующие к интуиции, перевести на количественный язык, вопрос может прозвучать так: «Какую долю видимой изменчивости следует ликвидировать в процессе сглаживания?» или «Сколько точек достаточно в сглаженной линии для отображения тренда?» В зависимости от ответов следует назначать ширину окна. Если для эмпирических данных с рис. 26 хочется сохранить сглаженные значения низких температур в диапазоне 435−535, а изменчивость температуры в диапазоне 535−635 минут не важна, то ширина окна должно быть около 100. Если же перепад температур в диапазоне времени 535−635 важен для анализа, то ширина окна должна быть около 30. Путем перебора значений h можно выбрать окончательный вариант.

Вместе с тем можно использовать формальные алгоритмы поиска лучших решений, например рандомизацию и кросс-проверку (Мастицкий, Шитиков, 2014). Общий смысл такой проверки состоит в том, чтобы многократно на серии случайных выборок (извлеченных из исходных данных) определять параметры модели, а на другой серии рандомизированных выборок оценивать погрешность прогноза модели (ŷ) относительно реальных значений (y) по сумме квадрата отклонений: SSE = Σ(y − ŷ)²/n. Чем меньше ошибка, тем лучше модель с принятыми параметрами описывает действительность.

При сглаживании по всему ряду исходных значений наименьшую ошибку будет иметь кривая, прошедшая через все точки, однако такой результат противоречит цели сглаживания. Если же сглаживание проводить многократно на небольших выборках, случайно отобранных значений из исходного ряда, то даже при одной и той же ширине окна сглаженные ряды будут различаться по точности воспроизведения исходных данных. Перебирая размеры окна, можно найти оптимальный вариант. Лучшим параметром сглаживания (h) можно считать такой, при котором средние погрешности прогноза будут минимальны.

В примере подбирали лучшую ширину окна для ядерного сглаживания температуры тела гадюки в дневные часы. Объемы случайных выборок (nn) составили от 1/3 до 1/7 от исходного ряда (n). Перебрали 295 значений ширины окна (nstep=295) от 5 до 300 отсчетов. Для оценки средней ошибки (SSE) каждого варианта ширины окна (h) по 100 раз брали случайные выборки, рассчитывали ошибки (sr) и усредняли.

head(ve<-read.csv("tve202280_5_10_46.csv")) id<-c(435:867) ; xx<-round(ve[id,3],2) ; n<-length(id) num nstep=295 ; SSE300) ; sr<-1:100 #-------------------------------------- for (i in 1:nstep){ for (r in 1:100){ j<-sort(sample(num,nn)) ; x<-xx[j] y<-ksmooth(j,x,ban=h[i])$y ; m<-sum(complete.cases(y)) sr[r]<-sum(((x-y)^2)/m,na.rm=TRUE) } SSE[i]<-mean(sr) } #-------------------------------------- SE<-filter(SSE,rep(0.2,5)) ; fh<-which(SE==min(SE,na.rm=TRUE)) plot(SE,type='l',xlab='h') ; fh #-------------------------------------- y<-ksmooth(num,xx,ban=fh)$y plot(num,xx,col='grey',cex=.7,xaxt='n',ylab='tv') ; lines(num,y,lwd=2) ind<-seq(1,n,20) ; axis(1,at=num[ind],id[ind])

В примере по мере роста ширины окна средние ошибки (SE) вначале падали, затем снова стали возрастать (рис. 26, А). Окончательной выбирали ту ширину окна, при которой ошибка была минимальной.

Оказалось, что в этой методике окончательный результат будет зависеть от выбранной величины выборок для оценки ошибки сглаживания. Однако число возможных прогонов резко сокращается: обучающие выборки объемом n/3−n/9 дают всего 7 вариантов ответов, из которых остается выбрать лучший. Конечно, можно было составить скрипт поиска минимальной SEE с помощью процедур минимизации (например, optim()). Для упрощения объяснений мы выбрали перебор.

 

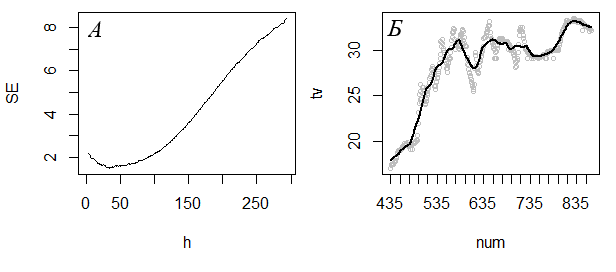
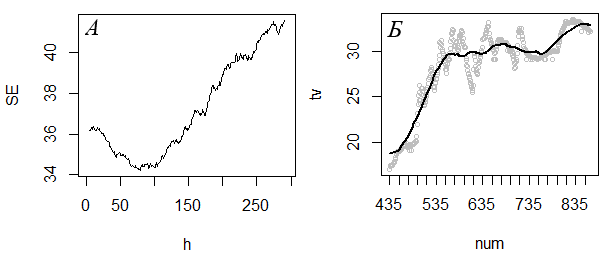
Рис. 26. Изменение величины средней погрешности (SE) сглаженного ряда температуры тела гадюки (tv) для разных значений ширины окна (h) (А) и результат ядерного сглаживания динамики дневной температуры тела (Б) для разных объемов тренировочного ряда x: вверху − для n/3 получили h = 32, внизу − для n/7 получили h = 79

Fig. 26. The change in the mean error (SE) of the smoothed viper body temperature series (tv) for different values of window width (h) (A) and the result of nuclear smoothing of the dynamics of daytime body temperature (Б) for different volumes of the training series x: at the top − for n/3 we got h = 32, at the bottom − for n/7, we got h = 79

Заключение или выводы

Чтение специальной литературы показывает, что в самых разных областях науки разработаны и используются аналогичные методы количественного преобразования данных, когда короткий ряд чисел, скользя вдоль длинного ряда чисел, преобразует его в третий ряд чисел. В зависимости от времени разработки и области исследований авторы используют разные, но синонимичные термины, а идеология скользящего окна остается одинаковой. В то же время методы преобразования (свертки) ряда x в ряд y постоянно развиваются и меняются в зависимости от объектов исследования.

Все рассмотренные выше методы (и их разнообразные варианты) − подстановка, скользящая медиана, скользящая средняя, фильтры, локальная регрессия, сплайны, ядерная регрессия, оценка ядерной плотности − используют принцип скользящего окна и свертки. Даже такие методы анализа временных рядов, как автокорреляция, кригинг, разложение Фурье, спектральный анализ, компонентный анализ, многомерное шкалирование, можно рассматривать как вариант применения скользящего окна с переменной шириной.

Отдельную область составляет теория и практика применения метода скользящего окна на двумерных и многомерных пространствах. Картография, обработка изображений, многомерная классификация данных, многомерная ядерная регрессия, вейвлет-анализ, сверточные нейронные сети − вот некоторые направления развития рассматриваемой идеологии, которую можно успешно применять в экологических исследованиях.

Библиография