Коросов А. В. Решение задачи классификации с помощью нечеткой логики // Принципы экологии. 2024. № 3. С. 96–116. DOI: 10.15393/j1.art.2024.15002

Выпуск № 3

Методы экологических исследований

pdf-версия статьи

574.4:510.644.4

Решение задачи классификации с помощью нечеткой логики

Введение

Нечеткая логика призвана трансформировать множество неточных фактов и соображений в конкретный вывод, решение, действие. Начиная с семидесятых годов алгоритмы нечеткой логики используются для управления роботами и производственными процессами (Рыбин, 2007). Нечеткая логика − это синтез аппарата формальной логики и теории множеств (Паклин, 2021). По мнению ряда авторов, теория нечеткой логики оказалась главным прорывом математики прошлого века (Ланге, 2018). В экологической сфере она позволяет классифицировать природные явления (объекты) (Меншуткин, 2010) в медицине − диагностировать заболевания (Харьков, 2011; Зюбова, 2013; Быков и др., 2016; Ramirez-Mendoza, 2022). Наработки нечеткой логики используются в близких дисциплинах − биометрике (boimetrics − распознавание личности по биологическим свойствам, Du, 2012) и биоинформатике (bioinformatics − моделирование структуры биологических макромолекул, Baldi, Brunak, 2001; Bandyopadhyay et al., 2007). Собственно биометрия (biostatistics, прежняя biometrics), широко используемая в экологических исследованиях, практически игнорирует эту область: ни в одном достаточно свежем учебнике по биометрии (Quinn, Keough, 2002; Дюк, Эмануэль, 2003; Chang, 2011; Джеймс и др., 2016; Соколов и др., 2016; Pagano, Gauvreau, 2018) нет предложений по использованию нечеткой логики. Основной лейтмотив нашей публикации состоит в популяризации этого метода количественной обработки экологических данных.

Цель сообщения − показать алгоритм конструирования классификационных построений в экологических исследованиях с помощью аппарата нечеткой логики.

В нашем сообщении рассмотрен подход к решению задачи определения пола обыкновенной гадюки (Vipera berus L.) по качественным и количественным признакам. По мере изложения задач вводятся необходимые теоретические понятия. Расчеты выполнены в среде R (The R…, 2023). Все этапы можно повторить, выполняя представленные в тексте скрипты. Перед чтением статьи мы рекомендуем ознакомиться с кратким, но рельефным описанием изучаемой технологии (Палкин, 2021). Этот удачный текст поможет создать общее впечатление о методе, тогда как наш материал детально покажет все этапы осуществления процедуры.

Материалы

Данные по морфологии обыкновенной гадюки собраны нами в 1992−2023 гг. на островах Кижского архипелага (Коросов, 2010). В качестве источника данных служит обширная таблица, сокращенный вариант которой (datavip.csv, 325 записей) доступен по гиперссылке. Пол гадюк из представленной базы данных определялся по серии внешних морфологических признаков, часть из которых проанализирована в статье. Подтверждение определений пола выполнено при вскрытии около 50 особей.

Традиционные методы исследований

Нечеткая логика является развитием формальной («четкой») логики и решает в том числе похожие задачи, например классификацию особей по статусу. Рассмотрим решение задачи прижизненной диагностики пола обыкновенной гадюки сначала методами традиционной логики, а в следующем разделе − с помощью нечеткой логики.

Цель предстоящей работы состоит в том, чтобы составить логические правила, которые позволяют по внешним морфологическим признакам выявить среди гадюк самцов и самок. Сначала предстоит изучить экстерьерные признаки, выявить значения, характерные для разнополых особей, и в заключение построить логическую модель для идентификации пола. В качестве характеристик выступят следующие: окраска спины и хвоста, размеры тела и хвоста.

Для введения в метод понадобится ряд терминов формальной логики и теории множеств. Формальная (аристотелева) логика изучает методы правильного мышления и рассматривает три главных темы: понятия, суждения и «законы» логики (Свинцов, 1987).

Вводя биологическое понятие, например «хвост», о котором пойдет речь, нужно видеть весь путь становления этого понятия. Непосредственное чувственное восприятие конкретных хвостов гадюк сохраняем в памяти как представление о них. Опыт изучения разнообразных примеров приводит к абстрагированию от конкретного наполнения, к обобщению, собственно к понятию, относящемуся ко всем объектам данного класса: «хвост − это часть тела, орган животного, который включает в себя позвоночный столб и расположен позади ануса или клоаки». Определение понятия дается по правилам: определяемое равно определяющему, без логического круга, с положительным содержанием, видовые признаки следуют за родовыми. В нашем примере используются следующие понятия: тело, хвост, спина, окраска, размеры, пол.

(Здесь не обойтись без примеров ошибочных дефиниций. Так, непрофессионализм некоторых авторов Википедии виден по логическим ошибкам даже в простейших определениях: «Хвост... − отдел сегментированного тела, располагающийся позади анального отверстия и не содержащий кишечника» (https://ru.wikipedia.org/wiki/Хвост); налицо отрицательное содержание, т. е. ошибка в построении дефиниции. Однако известное определение Н. Винера «...информация − это... не вещество и не энергия...» (что, в принципе, позволяет добавить: «и не заячий хвостик»), на наш взгляд, не следует рассматривать как ошибку, но как умышленную провокацию, заставляющую исследователей глубже вникать в тему.)

Понятия объединяются в словесные конструкции − простые суждения, логически сочетающие субъект (предмет, «хвост») и предикат (характеристики, «длинный») и поэтому обладающие свойством истинности (ИСТИНА − это когда суждение соответствует наблюдению, и ЛОЖЬ − когда не соответствует). В формализованной теории множеств суждения обозначаются латинскими буквами (A, B...), а значения истинности — цифрами 0 и 1, в среде R − константами FALSE, TRUE. Утверждение «длинный хвост» (A) истинно, если перед нами самец гадюки, и ложно, если самка; для любой самки A = 0, для самца A = 1. Другое утверждение, «спина серая», для самцов истинно, B = 1, для самок − ложно, B = 0.

Память подсказывает, что для самцов истинными будут следующие суждения: спина серая, спина синяя, спина черная, хвост длинный, хвост (снизу) черный, тело длинное, тело короткое.

Сложные суждения объединяют серию простых суждений, которые занимают во фразе свои позиции. Находясь в пропозиции, они объединяются пропозициональными союзами. Для наших целей важны лишь три метода объединения простых суждений, три союза: конъюнкция (логическое И, ∩), дизъюнкция (логическое ИЛИ, ∪) и импликация (логическое ВЛЕЧЕТ, →). Сложное суждение обретает значение истинности в зависимости от истинности входящих в него суждений и способа их объединения (табл. 1).

 

Таблица 1. Значения истинности для суждения «самец» по характеристикам гадюк 

Хвост длинный, A	Спина серая, B	A ∩ B	A ∪ B	A → B
0	0	0	0	1
0	1	0	1	1
1	0	0	1	0
1	1	1	1	1

  

Смысл операций, представленных в табл. 1 для гадюк из нашего примера, очевиден. Конъюнкция (∩). Это не самец, когда хвост не длинный И спина не серая (0 ∩ 0 = 0), когда хвост не длинный И спина серая (0 ∩ 1 = 0), когда хвост длинный И спина не серая (1 ∩ 0 = 0). У самца обязательно длинный хвост и серая спина (1 ∩ 1 = 1). Дизъюнкция (∪). Это может быть самец, когда ИЛИ хвост длинный (1 ∪ 0 = 1), ИЛИ спина серая (0 ∪ 1 = 1), ИЛИ и хвост длинный, и спина серая (1 ∪ 1 = 1); это не самец, если хвост не длинный и спина не серая (0 ∪ 0 = 0). Импликация (→). Когда хвост не длинный, то спина не серая (0 → 0 = 1); импликация истинна (это не самец). Когда хвост длинный, то спина серая (1 → 1 = 1); импликация истинна (это самец). В отличие от первых союзов, импликация содержит неравнозначные суждения, второе важнее. Поэтому если верное (второе) суждение получено из неверного (первого) суждения, в целом оно считается истинным. Все равно, какой хвост, когда спина серая (0 → 1 = 1), импликация истинна. Независимо от того, какой хвост, когда спина не серая (1 → 0 = 0), импликация ложна (это не самец).

Сложные суждения должны подчиняться «законам логики»: тождества, непротиворечия, исключения третьего. Формальная логика имеет дело только с двумя значениями − ИСТИНА и ЛОЖЬ: если данная особь самец (ИСТИНА), то это не самка (ЛОЖЬ), и наоборот. Здесь проявляется закон исключения третьего: суждение может быть либо истинным, либо ложным, третьего не дано. Стремление к однозначности характерно для интерпретации человеком явления окружающего мира, когда все хочется свести к дихотомии: «Крым наш или нет?», «пить вредно или полезно?». И это понятно, поскольку управленческие решения должны приниматься только тогда, когда ситуация «созреет»; таков, например, механизм одноконтурной отрицательной обратной связи. Дискретное, в т.ч. дихотомическое, решение при моделировании во многих случаях полезно, но это не единственный путь.

Теперь есть все термины, чтобы построить логическую модель для идентификации пола гадюк. Любая модель включает в себя входные переменные (X), действия над ними (f) и выходные переменные (Y) (Коросов, 2002).

 

Выходная переменная − это пол особи со значениями «самец» (y = 1) и «самка» (y = 0). Для большей наглядности можно эти значения отобразить на диаграмме, где по оси абсцисс отложить значения пола, а по оси ординат − истинность этого утверждения (иначе − нашу уверенность в конкретном диагнозе,  μ) (рис. 1).

 

  

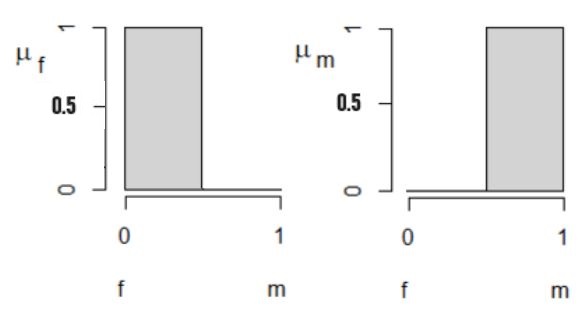
Рис. 1. Выходные функции принадлежности  μ_F «самки» и  μ_M «самцы» для признака «пол» (y)

Fig. 1. The output membership functions µ_F "females" and µ_M "males" for the attribute "sex" (y)

 

Входные переменные − это морфологические характеристики особей: окраска спины и хвоста, размер тела и хвоста (табл. 2). Вспоминая свою многолетнюю работу с гадюками (Коросов, 2010), можно отметить пять основных градаций окраски спины: коричневая (самки), зеленая (самки), серая (самцы), синяя (самцы), черная (оба пола). У самцов хвост снизу почти весь черный, у самок на треть − желтый. Размер хвоста тоже отличается: он короткий у самок и длинный у самцов. По размерам тела гадюки обоего пола могут быть средними и крупными (мелкие молодые особи не рассматриваются, т. к. они однотипно окрашены в коричневые ювенильные тона).

 

Таблица 2. Обозначения и значения модельных переменных 

Свойство	Градации (термы)
Окраска спины (Color)	коричневая ( dark yellow)	зеленая (salad)	серая (grey)	синяя (blue)	темная (dark)
Окраска хвоста (Tail)	желтый (yellow)	черный (black)
Размер тела (Length total)	средний (small)	крупный (big)
Длина хвоста (Length caudal)	короткий (short)	длинный (long)
Пол (Sex)	самка (female) (y = 0)	самец (male) (y = 1)

 

Практика показывает, что одни характеристики однозначно указывают на самцов, например, самки не могут быть ни серыми, ни синими. Некоторые характеристики имеют смысл только в сочетании с какими-то другими, например, у средних самцов хвост короткий и неотличим от крупных самок, черную окраску могут иметь оба пола. Разные свойства отличаются по трудоемкости их получения, например, определить окраску хвоста снизу можно только поймав змею. По причине определенной опасности этой процедуры такое свойство нельзя рекомендовать как приоритетное; сначала следует понять, можно ли идентифицировать особь по другим характеристикам, дистанционно.

Действия над входными переменными − это логические операции преобразования входных переменных в выходные. Для диагностики пола особи необходимо отобразить такие сочетания значений изучаемых признаков, которые характерны для самок, и отдельно − которые характерны для самцов. Все возможные сочетания градаций этих характеристик отображены в обобщающей табл. 3. Часть сочетаний не была включена в таблицу, поскольку они невозможны. Например, в природе нет средних коричневых самок с желтым и длинным хвостом. Таким образом, была создана модель в виде правил классификации (см. табл. 3).

 

Таблица 3. Правила для диагностики пола обыкновенной гадюки

Входные переменные				Выходная переменная	Краткая запись правила
окраска спины, Co	окраска хвоста, T	размер тела, Lt	длина хвоста, Lc	пол, y	B∩T∩S∩L → y
коричневая	желтая	средний	короткий	самка	y∩y∩s∩s → 0
зеленая	желтая	средний	короткий	самка	s∩y∩s∩s → 0
серая	черная	средний	короткий	самец	g∩b∩s∩s → 1
синяя	черная	средний	короткий	самец	b∩b∩s∩s → 1
темная	черная	средний	короткий	самец	d∩b∩s∩s → 1
темная	желтая	средний	короткий	самка	d∩y∩s∩s → 0
коричневая	желтая	крупный	короткий	самка	y∩y∩b∩s → 0
зеленая	желтая	крупный	короткий	самка	s∩y∩b∩s → 0
серая	черная	крупный	длинный	самец	g∩b∩b∩l → 1
синяя	черная	крупный	длинный	самец	b∩b∩b∩l → 1
темная	черная	крупный	длинный	самец	d∩b∩b∩l → 1
темная	желтая	крупный	короткий	самка	d∩y∩b∩s → 0

 

Каждая строка из табл. 3 представляет собой сложное суждение, в котором для объединения пяти простых суждений используются три союза И (конъюнкция), а также союз ВЛЕЧЕТ (импликация): B∩T∩S∩L → y. Применяя рассмотренные ранее обозначения, все продукционные правила были записаны в символической форме.

Итак, логическая модель (см. табл. 3) построена. Теперь настает время воспользоваться результатами проделанной работы. Таблица дает однозначную идентификацию пола гадюки по описанным морфологическим признакам.

Проанализируем первые попавшиеся в Интернете картинки по запросу «vipera berus» (рис. 2). Гадюка серой масти (g∩... → 1) (https://avatars.mds.yandex.net/i?id=8bd188b4d5dde604dc081a659bcdd95f4d17ea98-4860111-images-thumbs&n=13) легко определяется как самец (y = 1); у крупной коричневой змеи виден короткий и на треть желтый хвост (y∩y∩b∩s → 0) (https://avatars.mds.yandex.net/i?id=f440ff55dcee3023f7eea2fdbc6edfaa4932af31-10525373-images-thumbs&n=13), значит, это самка (y = 0).

 

                              

 Рис. 2. Фото из Интернета: самец и самка обыкновенной гадюки

Fig. 2. Photo from the Internet: male and female common viper

 

Представленный выше алгоритм классификации был основан на экспертном мнении (воспоминаниях) автора о наличии тех или иных показателей у разнополых гадюк. Во многих случаях представлений экспертов достаточно, чтобы можно было составить успешную классификацию, тем более что существуют методы, позволяющие путем итеративных опросов нескольких экспертов прийти к выравненным оценкам (Григорьева и др., 2018). Иногда и не существует других путей анализа ситуации. Однако в нашем случае мы можем обратиться к фактам, статистике и построить распределения выбранных значений в изученной выборке (рис. 3) для уточнения диагностических свойств рассмотренных характеристик. В среде R распределение показателя позволяют построить функции table() для качественных данных, hist() − для количественных. В расчетах использована обучающая выборка из 250 экз., выбранных случайно. Расчет и построение частотных распределений входных переменных (см. рис. 3) выполняется в первой части скрипта 01 memfun.R.

   

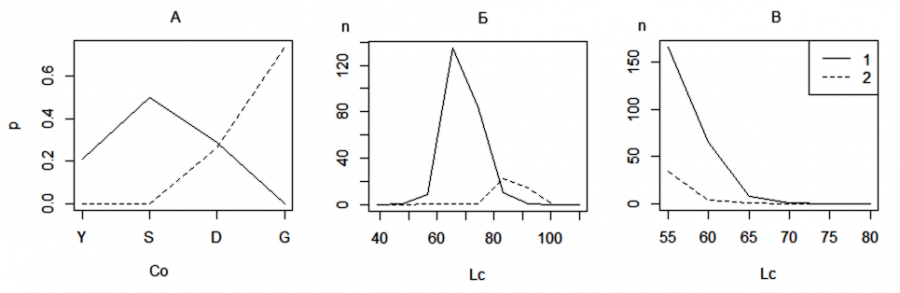
Рис. 3. Распределение самок (1) и самцов (2) гадюки по окраске спины (Co, А), по длине хвоста (Lc, Б) и по длине тела (Lt, В)

Fig. 3. Distribution of female (1) and male (2) vipers by back coloration (Co, A), tail length (Lc, Б) and body thickness (Lt, В)

 

Анализ распределений показывает, что у разных полов есть представители со всеми вариантами окраски, даже одна серая самка! Утверждение (суждение) «серая спина» для самцов оказалось не абсолютно истинным, B ≠ 1. Еще хуже оказалась ситуация с длиной хвоста: трансгрессия между распределениями для разнополых животных «на глаз» больше половины от размаха выборки. Иначе говоря, вопреки экспертному мнению, утверждение «у самцов хвост длинный» далеко от истины, А < 1.

Итак, реальность указывает на то, что экспертные бинарные утверждения не были абсолютно истинными. Если стоит цель описать действительность, то категории «истинность» и «ложность» должны быть не дискретными целочисленными, но непрерывными дробными.

Собственно в этом и состоит переход от четкой логики к нечеткой: с подачи автора, Л. Заде (1976), истинность стала рассматриваться как переменная, которая принимает не два, а множество разных значений: «очень истинно», «более-менее истинно», «не очень ложно» и т. д., и выражаться дробным числом в диапазоне от 0 до 1.

Оригинальные методы исследований

В стремлении включить в логические категории все многообразие мира, автор теории нечеткой логики (Заде, 1975) приблизил ее к естественному языку, который в большей мере соответствует действительности, чем формальная бинарная логика Аристотеля. Теорию и приложения нечеткой логики можно найти во многих публикациях (Рыбин, 2007; Григорьева и др., 2018; Ланге, 2018; Чернов, 2018 и др.).

 

Функция принадлежности

 В первую очередь было предложено отказался от дискретной степени истинности и вместо двух значений ЛОЖЬ (0) и ИСТИНА (1) использовать дробную степень истинности, которая была названа «функция принадлежности» (membership function, обозначается MF или μ). В литературе можно найти разные синонимичные обозначения для этой функции − характеристическая, совместимости, соответствия, уверенности, истинности. В каждом случае имеется в виду «степень принадлежности определенного значения характеристики x к данному классу объектов». Эта степень принимает дробные значения в пределах от 0 до 1 (Заде, 1975).

Функции принадлежности могут быть заданы, исходя из теоретических представлений, мнений экспертов или с опорой на эмпирические данные.

Функцию принадлежности можно задать графически или аналитически, с помощью формул (Чернов, 2018). Часто используют функции в форме треугольника, трапеции, гауссианы и логита (рис. 4).

 

 Рис. 4 . Варианты форм функции принадлежности

Fig. 4. Variants of the forms of the membership function

 

Для треугольной функции принадлежности аналитическая форма определяется тремя значениями абсциссы для левой (a), средней (b) и правой (c) вершин треугольника, в которых функция принадлежности равна 0, 1, 0; промежуточные значения MF вычисляются по формуле:

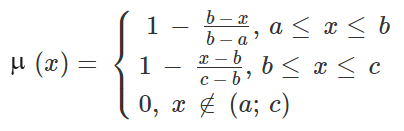
Трапеция задается четверкой значений x (a, b, c, d), которым соответствуют значения MF: 0, 1, 1, 0. Промежуточные значения MF вычисляются по формуле:

 

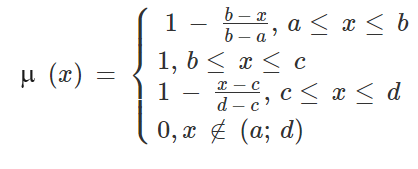
Ключевые точки (a, b, c, d) задаются, исходя из теоретических или практических соображений. Частным случаем трапеции можно считать прямоугольник, для задания которого достаточно всего двух значений − одной абсциссы и одной ординаты (см. выше).

Функция принадлежности может быть задана гауссовой кривой с двумя параметрами (средней M и стандартным отклонением S): μ_x = a * exp{−[(x − M) / S]²}. В этом случае предварительно нужно изучить статистические свойства базовой переменной x и назначить параметры M и S.

Для той же цели можно использовать формулу логита: μ_x = 1/(1 + exp(−(a₀ + a₁ * x)), заранее подбирая параметры кривизны (a) и смещения. Для моделирования двух альтернативных термов удобнее всего выбрать именно этот вариант.

Параметры функций принадлежности в процессе работы над моделью могут быть изменены, в т. ч. с помощью методов оптимизации.

* * *

Решая поставленную задачу, для начала составим функции принадлежности в графической форме. Для этого найдем относительные веса тех или иных значений для каждой группы, используя ранее полученные распределения.

Так, окраску D (черную) имеют 69 самок из 237 (0.29 из 1) и 10 самцов из 39 (0.26 из 1) (табл. 4). Рассчитав отношение долей (0.29 и 0.26) к сумме (0.55), находим, что при обнаружении, например, черной особи (Dark) степень уверенности в том, что это самка, составит 0.52, что самец − 0.48.

 

Таблица 4. Расчет значений функции принадлежности μ_Co для показателя окраски Co 

		Варианты окраски спины
Показатель	Пол	Yallow-dark	Salad	Dark	Grey	Сумма
Число самок	f	50	118	69	0	237
Число самцов	m	0	0	10	28	38
Доля от самцов	f	0.21	0.5	0.29	0	1
Доля от самцов	m	0	0	0.26	0.74	1
μCoF	f	1	1	0.52	0
μCoM	m	0	0	0.48	1

 

Расчет эмпирических входных функций принадлежности выполняется во второй части скрипта 01 memfun.R. Все рассчитанные эмпирические значения функций принадлежности были записаны в файлы 'mfCo.csv', 'mfLc.csv', 'mfLt.csv' и представлены на диаграмме (рис. 5). Для упрощения рассчетов данные по окраске хвоста опустили.

 

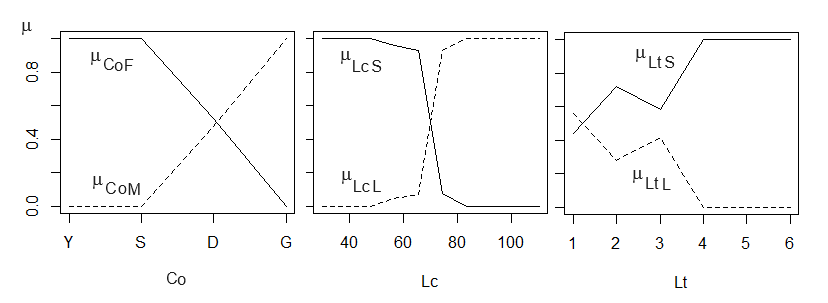
Рис. 5. Функции принадлежности для показателей окраска спины (Co) («цветная, самочья», μ_CoF; «бесцветная, самцовая», μ_CoM), длина хвоста (Lc) («хвост короткий», μ_LcS; «хвост длинный», μ_LCL) и длина тела (Lt) («тело короткое», μ_LtS; «тело длинное», μ_LtL)

Fig. 5. Accessory functions for indicators back coloration (Co) ("colored, female", µ_CoF; "colorless, male", µ_CoM), tail length (Lc) ("tail short", µ_LcS; "tail long", µ_LCL) and body length (Lt) ("body short", µ_LtS; "body long", µ_LtL)

 

Рассмотрим показатель «длина хвоста» (Lc) для класса объектов «самки гадюки» (см. рис. 3, 5). Не все значения длины хвоста принадлежат этому классу. Значения менее 50 мм, действительно, принадлежат только самкам (см. рис. 3, 5), значения от 50 до 70 мм частично принадлежат не только самкам, но и самцам; …; ни одно значение более 90 мм не принадлежит самкам. По этому описанию (используя частоты распределения) можно построить график, соответствующий ходу функции принадлежности значений длины хвоста, обнаруженной у самок гадюки. От 30 до 50 мм она будет равна единице, затем начнется снижение, и с 90 мм она будет равна нулю (см. рис. 5). Поскольку все же часть значений из этого ряда встречается и у самцов, эту функцию принадлежности следует назвать «кроткий хвост» (μ_LcS). Аналогичное построение нужно выполнить и для самцов (см. рис. 5), построив функцию принадлежности «длинный хвост» (μ_LCL).

Для конкретных значений переменной Lc первый график μ_LсS читается так: для промера Lс = 60 мм с уверенностью на 90 % (μ_LcS = 0.9) мы можем утверждать, что хвост короткий. Для того же значения на втором графике μ_LcL: утверждение «хвост длинный» для Lс = 60 мм истинно на 10 %. Важно отметить, что отдельные функции принадлежности − это как бы прежние дискретные суждения («у самцов хвост длинный»), которые в новой интерпретации расширились, разрослись до серии количественных оценок истинности, отображаемых в виде графика функции.

В дальнейшем при упоминании термина «функция принадлежности» перед внутренним взором читателя должен возникать образ одной кривой линии графика, отражающего соответствие всех изучаемых значений признака x − одному из классов.

Таким образом, говоря о каком-то свойстве одной группы в рамках нечеткой логики, мы имеем в виду два ряда значений: 1) базовую переменную (это собственно промеры, например, x₁, длина хвоста, варьирующая от 20 до 110 мм) и 2) функцию принадлежности (степень уверенности, что эти числа принадлежат данной группе, μ, варьирующей от 0 до 1).

Рассматривая все эти графики, по-прежнему можно видеть, что обычно самки крупнее, у самцов хвост длиннее, серые особи − самцы, а зеленые − самки. Однако теперь прежние простые однозначные суждения «расширились», получив плавные количественные характеристики, т. е. они стали полнее описывать действительность. Став функциями принадлежности, эти утверждения не потеряли смысла логических суждений (со своей степенью истинности). Именно поэтому над ними можно производить логические операции, строить логические модели, т. е. соединять пропозициональными союзами в сложные логические суждения.

 

Лингвистическая переменная

 Автор теории нечеткой логики предложил название «лингвистические переменные» для подобных многозначных характеристик. В примере их три: «окраска спины гадюки», «размер хвоста гадюки», «размер тела гадюки». Обозначение «лингвистическая» (или «словесная») эти переменные получили потому, что они призваны словами охарактеризовать какие-то градации. Так, «длина тела» (Lt) включает две градации, два качества особей, обозначенные словами «длинное тело» (рис. 5: 1) (в основном самки) и «короткое тело» (рис. 5: 2) (в основном самцы). В нашем примере лингвистическая переменная «длина тела» составлена из двух функций принадлежности (называемых еще «термы»). Две другие лингвистические переменные − «длина хвоста» и «окраска спины» также имеет по два терма, по две функции принадлежности. На диаграмме (рис. 5) показаны три лингвистические переменные. В строгое определение лингвистических переменных входят не только список термов, значения базового признака x и функции принадлежности μ_x, но и другие характеристики. Однако пока достигнутого объема знаний достаточно для построения нашей модели.

 

Построение логической модели (продукционные правила)

Новая логическая модель имеет типичную структуру: входные переменные в результате некоторых действий над ними должны превращаться в выходные переменные (рис. 6).

Однако на этом пути «четкие» входные переменные (имеющие физическую размерность − граммы, секунды, миллиметры, x, y) преобразуются в «нечеткие» величины − функции принадлежности (μ_x, μ_y), выражающие степень соответствия конкретных значений тем или иным классам объектов. Такое преобразование названо фаззификацией. Далее выполняются некие действия (по определенным правилам) над преобразованными входными величинами, в результате получают преобразованную выходную величину (μ_y). Затем выполняется обратное преобразование нечеткой переменной μ_y в «четкую» величину, выходное модельное значение y’. Эта операция названа деаззификация.

 

Рис. 6. Схема моделирования с помощью аппарата нечеткой логики

Fig. 6. The scheme of modeling using the fuzzy logic apparatus

 

Вернемся к примеру.

Выходная лингвистическая переменная («пол» со значениями y = 1 «самец» и y = 0 «самка») по-прежнему задана как два терма (прямоугольной формы) со значениями функций принадлежности 0 и 1 (см. рис. 1).

Входные лингвистические переменные «окраска спины», «длина хвоста», «размер тела» заданы в виде графиков функций принадлежности μ_Co, μ_Lc, μ_Lt для базовых переменных Co, Lc, Lt (см. рис. 5).

Действия над входными переменными − это логические операции преобразования входных лингвистических переменных в выходные лингвистические переменные. В примере смысл этих операций состоит в том, чтобы, получив характеристики конкретных особей, можно было оценить, насколько хорошо они соответствуют характеристикам самок и самцов.

Существует несколько алгоритмов нечеткого моделирования; ниже рассмотрен алгоритм Мамдани (Осовский, 2002; Григорьева и др., 2018; Чернов, 2018).

 

Продукционные правила для расчета выходных функций принадлежности

Общая формула нечеткого логического вывода выглядит так же, как и для формальной логики μ_Co ∩ μ_Lc ∩ μ_Lt → μ_S. Однако из-за изменения смысла входных переменных операции конъюнкции, дизъюнкции и импликации в нечеткой логике приняли форму действий над множествами, это операции пересечения, усечения, объединения.

Конъюнкция становится пересечением множеств в точке x:

μ_FM = μ_Co ∩ μ_Lc ∩ μ_Lt = min(μ_Co, μ_Lc, μ_Lt ).

Импликация принимает смысл усечения выходной функции принадлежности.

Дизъюнкция становится объединением усеченных множеств в точке x:

μ_FM = μ_F1 U μ_F2 U … U μ_M7 U μ_M8 = max(μ_F1 ..., ... μ_M8).

Используя эти операции, составляем модель − таблицу продукционных правил (табл. 5), которые позволяют по конкретным значениям характеристик (Co, Lc, Lt) для каждой особи определить пол (y).

С формальной стороны продукционные правила должны строиться так, чтобы рассматривать все возможные сочетания функций принадлежности (как это было сделано в табл. 5). Если какие-то сочетания невозможны, то их не включают в таблицу и не используют в расчетах. В нашем примере все три входные функции имеют по два терма, значит, общее число комбинаций термов равно восьми: 2³ = 8. 

Составление продукционных правил представляет собой не формальный, а основной, интеллектуальный, этап работы при моделировании с помощью нечеткой логики. Для каждого сочетания входных функций принадлежности нужно подобрать такую выходную функцию принадлежности, чтобы она была адекватна реальности. При этом необходимо учитывать все наблюдаемые сочетания характеристик у разнокачественных объектов. Например, даже если особь имеет светлую самцовую окраску, но короткий хвост и длинное тело, это явно самка (правило 6). Если построенные правила не охватывают всех вариаций реальности, значит, нужно увеличивать число термов и расширять спектр возможных ситуаций, строить дополнительные продукционные правила.

  

Таблица 5. Продукционные правила для диагностики пола обыкновенной гадюки

	Входные лингвистические переменные с градациями			Выходная лингвистическая переменная
№	окраска спины (Co:Colored/Gray/Dark)	длина хвоста (Lc: Short/Long)	размер тела (Lt: Short/Long)	пол (S: M/F)
1	F	S	S	F
2	F	S	L	F
3	F	L	S	M
4	F	L	L	F
5	M	S	S	M
6	M	S	L	F
7	M	L	S	M
8	M	L	L	M
Выходная переменная: y = точка равновесия (max(min(μCo, μLc, μLt))

 

Возможна и более компактная форма записи тех же правил:

min(μ_CoF, μ_LcS, μ_LtS) → μ_F

min(μ_CoF, μ_LcS, μ_LtL) → μ_F

min(μ_CoF, μ_LcL, μ_LtS) → μ_M

min(μ_CoF, μ_LcL, μ_LtL) → μ_F

min(μ_CoM, μ_LcS, μ_LtS) → μ_M

min(μ_CoM, μ_LcS, μ_LtL) → μ_F

min(μ_CoM, μ_LcL, μ_LtS) → μ_M

min(μ_CoM, μ_LcL, μ_LtL) → μ_M

 Последовательно рассмотрим смысл пересечения, усечения и объединения функций принадлежности для правил 1 и 7, представленных в табл. 5.

 Правило 1. min(μ_CoF, μ_LcS, μ_LtS) → μ_F означает, что для некоей особи неизвестного пола, имеющей индивидуальные значения трех переменных (самочья цветная окраска, короткий хвост, короткое тело − F, S, S), мы сначала определяем три значения функции принадлежности (μ_CoF, μ_LcS, μ_LtS), затем выбираем наименьшее (рис. 7). Отыскивая самое слабое звено в наших суждениях, мы выбираем минимальный, но тем самым гарантированный результат. После этого выбора мы усекаем (→) функцию принадлежности «самки» (μ_F) по этому уровню, получая определенную степень уверенности, что при данном конкретном сочетании значений (F, S, S) перед нами самка.

Так, конкретная темная особь с хвостом 80 мм и телом 57 см (Co = D, Lc = 80, Lt = 57) по графикам функций принадлежности получает три значения (μ_CoF = 0.52, μ_LcS = 0.04, μ_LtS = 0.58), из которых выбираем минимальное 0.04. Теперь переносим (→) эту величину на диаграмму выходной переменной μ_F (см. рис. 1) и отсекаем от нее фигуру выше границы μ_F = 0.04 (см. рис. 7). Итак, гарантированная уверенность в том, что особь с характеристиками (Co = D, Lc = 80, Lt = 57) по первому правилу является самкой, составляет 0.04.

Задача состоит в том, чтобы выполнить расчеты по всем правилам для данной особи с неизвестным полом. Для примера остановимся на расчете правила 7, затем рассмотрим результаты вычислений по всем остальным правилам. 

 

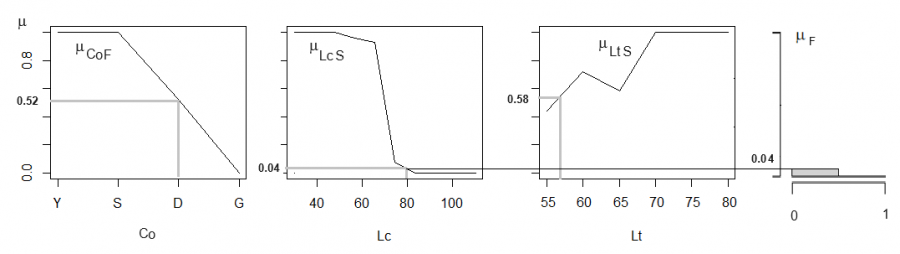
Рис. 7. Применение правила 1: определение значений трех функций принадлежности ( μ_CoF = 0.52, μ_LcS = 0.04, μ_LtS = 0.58) к категории «самка» отдельной особи с характеристиками Co = D, Lc = 80 мм, Lt = 57 см; конъюнкция (пересечения) функций принадлежности и отсечение значения от терма «самка» для выходной переменной «пол»

Fig. 7. Application of rule 1: determination of the values of three membership functions (µ_CoF = 0.52, µ_LcS = 0.04, µ_LtS = 0.58) to the category "female" of an individual with characteristics Co = D, Lc = 80 mm, Lt = 57 cm; conjunction (intersection) of membership functions and cutting off the value from the term "female" for the output variable "gender"

 

Правило 7. min(μ_CoM, μ_LcL, μ_LtS) → μ_M означает, что для той же особи неизвестного пола, имеющей индивидуальные значения трех переменных (Co = D, Lc = 80, Lt = 57) мы по графикам определяем три значения (μ_CoF = 0.48 μ_LcL = 0.98 μ_LtS = 0.58) функции принадлежности и выбираем наименьшее μ = 0.48 (рис. 8). Переносим (→) эту величину на диаграмму выходной переменной μ_M (см. рис. 1) и отсекаем от нее фигуру по граничному значению μ_M = 0.48 (рис. 8). Итак, правило 7 утверждает, что со степенью уверенности 0.48 эта особь является самцом.

  

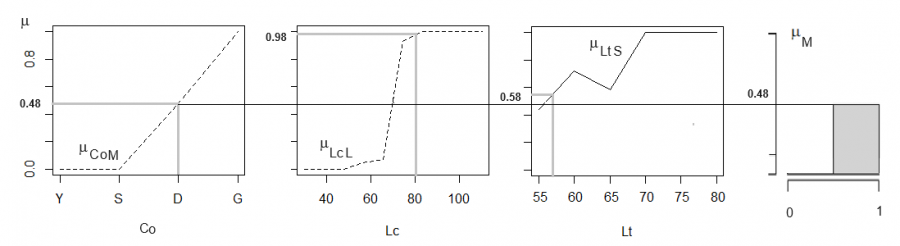
Рис. 8. Применение правила 7: определение значений трех функций принадлежности (μ_CoF = 0.48, μ_LcS = 0.98, μ_LtS = 0.58) к категории «самец» отдельной особи с характеристиками Co = D, Lc = 80 мм, Lt = 57 см; конъюнкция (пересечения) функций принадлежности и отсечение значения от терма «самец» для выходной переменной «пол»

Fig. 8. Application of rule 7: determination of the values of three membership functions (µ_CoF = 0.48, µ_LcS = 0.98, µ_LtS = 0.58) to the category "male" of an individual with characteristics Co = D, Lc = 80 mm, Lt = 57 cm; conjunction (intersection) of membership functions and cutting off the value from the term "male" for the output variable "gender"

 

Как можно было видеть, для отдельной особи нужно определить 6 значений для 6 функций принадлежности (табл. 6), а затем проанализировать все возможные их комбинации и для каждого случая определить значение выходной лингвистической переменной μ (табл. 7).

 Всего для 8 правил рассчитываем 4 значения для выходного терма μ_F и 4 значения для μ_M. 

 

Таблица 6. Значения всех функций принадлежности для особи с характеристиками Co = D, Lc = 80 мм, Lt = 57 см 

	μCo	μLc	μLt
S	0.52	0.04	0.58
L	0.48	0.96	0.42

 

Таблица 7. Поиск точки равновесия выходной лингвистической переменной для особи с характеристиками Co = D, Lc = 80 мм, Lt = 57 см 

Правила	μCo	μLc	μLt	min	μF	μM
1	0.52	0.04	0.58	0.04	0.04
2	0.52	0.04	0.42	0.04	0.04
3	0.52	0.96	0.58	0.52		0.52
4	0.52	0.96	0.42	0.42	0.42
5	0.48	0.04	0.58	0.04		0.04
6	0.48	0.04	0.42	0.04	0.04
7	0.48	0.96	0.58	0.48		0.48
8	0.48	0.96	0.42	0.42		0.42
max					0.42	0.52
Баланс					y = 0.53

 

Обобщение выходных функций принадлежности 

Формула объединения значений всех термов выходной лингвистической переменной «пол» – это логическое ИЛИ, дизъюнкция, которая в терминах теории множеств превращается в поиск максимального значения: μ_M = max (μ_f, μ_m). Смысл такой процедуры можно понимать как поиск лучшего для наших целей решения. Поскольку цель состоит в диагностике пола, нужно брать самые высокие оценки уверенности в том, что данная особь самка или самец. В результате этого выбора получаем фигуру, совмещающую максимальные значения функции принадлежности к самкам и самцам (рис. 9).

  

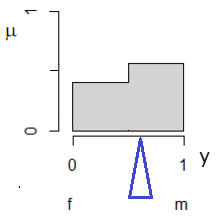
Рис. 9. Объединенная выходная функция принадлежности μ для значений пола y  с отметкой центра равновесия (0.53) для особи с характеристиками Co = D, Lc = 80 мм, Lt = 57 см

Fig. 9. The combined output function of membership μ for the values of sex y with the mark of the center of equilibrium (0.53) for an individual with characteristics Co = D, Lc = 80 mm, Lt = 57 cm

 

Расчет выходного значения y

 Последняя процедура нашей модели – определение единственного «четкого» выходного значения y’ (Чернов, 2018), собственно пола для конкретной особи. Один из методов такой оценки состоит в определении точки равновесия полученной фигуры для выходной лингвистической переменной по формуле: y = Σ(μ*y) / Σμ.

Поскольку выходные функции принадлежности мы задали в форме прямоугольника, в качестве абсциссы (y) можно взять единственные значения – центры левого и правого прямоугольников (y_F = 0.25 и y_M = 0.75). 

В качестве ординат нужно взять относительные веса выходных функций принадлежности: 

w0 = 0.42/(0.42 + 0.52) = 0.45, w1 = 0.52/(0.42 + 0.52) = 0.55.

Расчеты дали величину: y’ = 0.25*w0 + 0.75*w1 = 0.53.

Поскольку величина 0.5 была ранее принята как пограничное значение между самцами и самками, необходимо заключить, что для данной особи (y = 0.53 > 0.5) чаша весов склоняется в сторону самцов (рис. 9 ОБ).

 

 Полный цикл моделирования в среде R

 Процедура моделирования с помощью нечеткой логики сводится к восьми этапам (метод Мамдани):

1. определение базовых переменных: это входные x и выходная y; 

2. задание функций принадлежности для выходной лингвистической переменной μ_y;

3. задание функций принадлежности для входных лингвистических переменных μ_x;

4. построение продукционных правил (конъюнкция и усечение);

5. задание формул обобщения промежуточных выводов (дизъюнкция);

6. задание формул расчета выходной переменной;

7. настройка модели (классификация обучающей выборки объектов);

8. верификация модели (классификация тестовой выборки объектов);

9. использование: классификация неизвестных объектов.

 Выполняя скрипты 01 memfun.R, 02 fuzzy steps.R, 03 fuzzy verific.R, можно в деталях изучить всю процедуру. Первый скрипт подготавливает эмпирические значения для расчета функций принадлежности, второй находит логистические формулы для функций принадлежности и с их помощью классифицирует особей из обучающей выборки. Третий скрипт определяет пол особей по тестовой случайной выборке и оценивает погрешность. Ниже будут даны пояснения для работы некоторых фрагментов кода.

 1. Определение базовых переменных. Скрипт 01 memfun.R читает значения «четких» входных переменных из файла datavip.csv: для 325 особей представлены значения пола (S), окраски спины (Co), длины хвоста (Lc), длины тела, больше 50 см (Lt > 50). Формирует массив v для обучающей выборки объемом 250 экз. и массив y для «четкой» выходной переменной.

nv<-250 v<-read.csv("vipdata.csv" )[-1][sample(1:325,nv),] y<-rep(0,1,nv)

 2. Для выходной лингвистической переменной заданы два массива с четырьмя нулями. Эта запись присутствует в скрипте 02 fuzzy steps.R в теле цикла расчетов для каждой особи.

yF<-yM<-rep(0,1,4)

 3. Входные функции принадлежности должны быть заданы в форме шести уравнений логистической регрессии, построенной по эмпирическим данным, представленным на рис. 5: одно уравнение для одной функции принадлежности. Для каждой переменной скрипт 01 memfun.R рассчитывает частоты эмпирических распределений и эмпирические функции принадлежности, которые записывает в следующие файлы: для окраски 'mfCo.csv', для длины хвоста 'mfLc.csv', для длины тела 'mfLt.csv' (табл. 8).

 

Таблица 8. Значения функций принадлежности для длины тела в файле mfLt.csv 

	V1	V2	V3	V4	V5	V6
	55	60	65	70	75	80
ddf	0.445	0.742	0.636	1	1	1
ddm	0.555	0.258	0.364	0	0	0

  

Скрипт 02 fuzzy steps.R, используя данные для всех переменных, рассчитывает функции принадлежности в форме логистической регрессии (с помощью функции glm()), формирует массив коэффициентов a (табл. 9) и записывает их в файл fuzzparameters.csv. Теперь функции принадлежности оказались гладкими (рис. 10).

 

Таблица 9. Коэффициенты a в уравнении логистической регрессии вида μ_x = 1/(1 + exp(−(a₁ + a₂*x)) для шести функций принадлежности 

	[1]	[2]
1	70.96563	-23.5829293
2	-70.96563	23.5829292
3	26.89796	-0.3853506
4	-26.89796	0.3853506
5	-11.04376	0.1935276
6	11.04376	-0.1935276

 

 

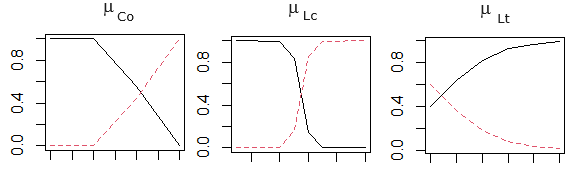
Рис. 10. Функции принадлежности, рассчитанные по формулам логистической регрессии

Fig. 10. Membership functions calculated using logistic regression formulas

 

4. В скрипте 02 fuzzy steps.R выполняется работа восьми продукционных правил для определения пола у особей. Для удобства пол задан как числовой массив se. Расчеты выполняются в цикле для каждой особи из группы случайно отобранных (в количестве nn экз.). Сначала задаются массивы для хранения значений выходных функций принадлежности (yF nn, yM). Затем формируется массив входных переменных (x), который содержит дублированные значения (x<‑cbind(s=se[j],v[j,3:5])[,c(2,2,3,3,4,4)]). Это позволяет с использованием коэффициентов a сразу рассчитать все значения функций принадлежности для данной особи (mf<-1/(1+exp(-(a[,1]+x*a[,2])))). Для наглядности полученные значения разносятся по ячейкам, имеющим говорящие названия (CoF – функция принадлежности «самочья окраска» и т.п.). Далее, в соответствии с рассмотренными выше правилами, выбираются наименьшие значения из сочетания входных функций принадлежности (min(CoF,LcS,LtS)...) и присваиваются соответствующим выходным функциям принадлежности (yF[1]...).

5. Формулы обобщения промежуточных выводов из правил включены в цикл расчета для каждой особи (скрипт 02 fuzzy steps.R) – это выбор максимального значения из четырех значений, рассчитанных (max(yF)...).

6. Формула расчета выходной переменной включена в цикл расчета для каждой особи (скрипт 02 fuzzy steps.R) и реализует рассмотренный выше метод поиска центра равновесия с помощью относительных весов: w0<-syF/(syF+syM) ; w1<-syM/(syF+syM) ; y[j]<-0.25*w0+0.75*w1.

7. Настройка модели состоит в снижении расхождений между прогнозом модели и реальными значениями. Снизить расхождение (невязку) можно, если целенаправленно менять модельные параметры, от которых зависит форма входных и выходных функций принадлежности. Когда параметры функций принадлежности принимаются умозрительно экспертами, такая настройка может привести к существенному улучшению работы модели. Однако в нашем примере параметрами модели являются коэффициенты логистической регрессии, построенной по реальным репрезентативным данным, и мы не имеем возможности произвольно менять эти коэффициенты. В то же время выборка, по которой выполняется расчет, имеет меньший размер (250 записей), чем исходные данные (325 записей), следовательно, можно несколько раз извлекать разные случайные выборки и остановиться на той, которая дает лучший прогноз. Степень прогностических возможностей построенной модели можно оценить по доле случаев совпадения прогноза по самцам и самкам (sum(round(y)==se)/nv). Представленный вариант модели дает погрешность 12 % (рис. 11).

 

 

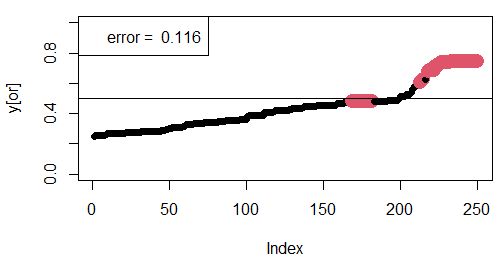
Рис. 11. Соответствие между прогнозными значениями y’ (упорядочены по возрастанию) и реальными значениями пола гадюк (самцы – крупные красные значки)

Fig. 11. The correspondence between the predicted values of y’ (sorted in ascending order) and the real values of the sex of the vipers (males – large red signs)

 

8. Верификация состоит в проверке точности прогноза пола по тестовой выборке, которая по большей части не участвовала в построении модели, в расчете коэффициентов для входных функций принадлежности. Для этого служит скрипт 03 fuzzy verific.R. Из исходной выборки (объемом 325 записей) извлекаются 100 случайных особей и выполняется идентификация пола. Серия прогонов показала, что доля правильных определений составляет от 0.86 до 0.93 (рис. 12).

  

 

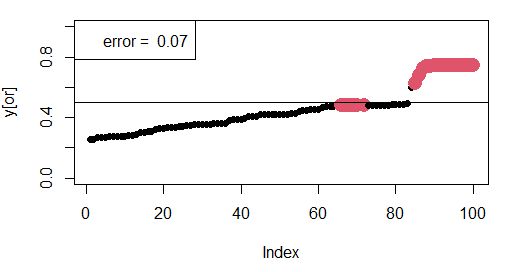
Рис. 12. Соответствие между прогнозными значениями y’ (упорядочены по возрастанию) и реальными значениями пола гадюк (самцы – крупные красные значки) для проверочной выборки

Fig. 12. The correspondence between the predicted values of y’ (sorted in ascending order) and the real values of the sex of the vipers (males – large red signs) for the test sample

 

9. Возможность использования модели для определения пола особей неизвестного качества должна определяться, исходя из требований к точности модели. На наш взгляд, погрешность в 10 % слишком велика для того, чтобы рекомендовать такую модель в практику герпетологических исследований. Оказалось, что изученных признаков недостаточно для уверенной диагностики пола, необходимы дополнительные характеристики. Возможно, если бы в анализ были включены показатели окраски низа хвоста, наличие «перетяжки» в области клоаки, толщина и масса особи, то погрешность модели снизилась бы до приемлемой величины.

Обсуждение

Первую тему для обсуждения можно выразить в вопросе: почему инструментарий нечеткой логики почти не используется в биолого-экологических исследованиях? Это не вполне понятно, ведь обсуждаемая методика довольно проста и с ее помощью, как мы показали, можно достичь целей классификации. В первую очередь, такой пробел можно объяснить тем, что в изданиях по биометрии описания методики либо вообще отсутствуют, либо даны очень кратко и то относительно лишь некоторых ее приложений (Шитиков, Розенберг, 2013). Что же касается специальной математической литературы, то для обычных биологов она вряд ли может служить эффективным пособием по применению, а упрощенные публикации из Интернета грешат неточностями и недосказанностью. Другую причину можно усмотреть в кажущейся умозрительности представления знаний в рамках этой методик. Разве можно добиться уточнения выводов, если вместо реальных характеристик анализировать наши представления о них, т.е. степень принадлежности реальных значений к тем или иным оценочным сущностям? Если есть факты (конкретная выборка значений), то может ли наше представление о них быть лучше самих фактов? В рамках моделирования этот вопрос можно переозвучить так: разве преобразование исходных данных может улучшить описание закономерности? И тогда ответ становится очевидным: конечно, может! Хорошо известно, что такие преобразования, как избавление от избыточной изменчивости или «выпрямление» соотношений (например, путем логарифмирования) позволяет точнее и полнее описать изучаемые биологические зависимости. Функции принадлежности выполняют именно эту роль – ликвидируют «эмпирические перекосы». Ближайшая аналогия − процедура неметрического шкалирования, которая сохраняет от конкретных фактов только свойство их упорядоченности, но не величину или пропорции. Функции принадлежности играют роль неких семантических целесообразных фильтров, которые уже на первом этапе обработки сообщают (приписывают) данным те или иные «веса» ценности, оперирование которыми и приводит к искомому результату. Функции принадлежности, на первый взгляд, могут показаться произвольно назначенными. Однако если настройку модели организовать как итеративную процедуру приближения к нужному результату (см. ниже), умозрительность построения быстро превратится в объективность. Поначалу странное впечатление может произвести и очень нестрогая формальность («нематематичность») всей процедуры построения нечеткой модели. Число тремов, форма функций принадлежности, состав и число продукционных правил − все назначается автором модели. Такая ситуация сильно контрастирует с привычными формализованными методами статистического анализа (регрессии, главных компонент и пр.). Все это так, однако свободу действий, гибкость модели можно считать большим плюсом этой методики, что открывает пути ее использования в самых разных отношениях, в т.ч. в возможности дополнять и усиливать формальные статистические процедуры, например кластерный анализ (C-means). Стоит отметить, что аналогичные неформальные этапы присутствуют и при нейросетевом моделировании (назначение функций активации, число входных, скрытых и выходных слоев и их элементов, структура связей между нейронами и пр.), что позволяет наращивать эффективность  и точность этого метода количественного исследования.

Вторая важная тема для обсуждения – это принципы назначения функций принадлежности, решение вопросов о выборе формы функции и методах задания параметров этих функций. Простые способы задания функций принадлежности (треугольник, трапеция) удобны для программирования в аналоговых устройствах управления бытовыми приборами (Acun, Cunkas, 2023). Они менее удобны для построения количественных описаний (классификаций) биологических объектов, поскольку содержат логические операторы, которые медлительны, требуют несколько строк кода и неудобны при настройке параметров методами оптимизации, а также непрерывно не дифференцируемы (Чернов, 2018). Для целей количественного анализа более удобны функции, задаваемые одной формулой с параметрами, определяющими форму кривой. Для краевых термов подходит логит, для промежуточных термов – гауссиана. Когда входные функции принадлежности назначаются по реальным данным, то предложенные формулы очень хорошо подходят для описания эмпирических распределений. Также следует отметить, что в качестве выходной функции принадлежности удобно использовать прямоугольные фигуры, заданные одним всего двумя числами – ординатой 1 и абсциссами 0.25 и 0.75 для альтернатив. Когда моделируется бинарная классификация (самка / самец), основное отличие прямоугольника от трапеции состоит в том, что первые фигуры не будут иметь трансгрессии, а трапеции будут. Здесь возникает вопрос: а имеет ли смысл эта трансгрессия? Во-первых, если цель − получить дихотомию, может быть, ее стоит заложить в выходные термы и точнее сформулировать продукционные правила? Во-вторых, трансгрессия трапеций относительно незначительна, ее роль теоретически непонятна («на всякий случай»?) и практически малозначима. Тогда, видимо, проще использовать прямоугольные функции. Подбирая вид функций принадлежности, следует помнить о запрете нарушать требование: каждое значение базовой переменной должно иметь свое значение функции принадлежности (Чернов, 2018).

Необходимо сказать и о процедуре настройки модели, которая может состоять как в изменении числа входных и выходных термов, так и в изменении значений параметров функций принадлежности. В нашем примере единожды рассчитанные значения параметров более не менялись. Главный аргумент состоял в том, что они характеризуют обширные выборки, значит, высоко репрезентативны и не будут меняться при дальнейшем росте объема выборки. По этой причине мы не рассматривали процедуру настройки параметров модели. В иных ситуация (например, когда исходная выборка мала) может потребоваться изменение параметров с целью подгонки модельных прогнозов под реальность. Другой случай – когда форма (параметры) функций принадлежности назначается умозрительно, исходя их неких теоретических представлений. Перестройка как структуры такой системы, так и количественных соотношений ее компонентов может составлять весь смысл построения такой модели. Процесс оптимизации построенной модели будет состоять из трех этапов: а) расчет стартовых значений параметров и выходных модельных значений, б) сравнение модельного выхода и реальных характеристик (оценка невязки), в) направленная модификация параметров с целью снижения невязки. Процедура повторяется до тех пор, пока невязка не перестанет снижаться. Как показала практика, если функции подгонки параметров функций принадлежности передать искусственной нейронной сети, то образуется очень функциональный синтетический комплекс – neuro-fuzzy – нейро-нечеткие системы, или нечеткие нейронные сети (Осовский, 2002; Научная сессия..., 2005; Анисимова, 2015). К сожалению, примеры использования нечетких нейронных сетей в близких к биологии областях известны только для моделирования структуры биологических макромолекул (Asman et al., 2023), для диагностики в медицине (Melin et al., 2021), для управления процессами в биотехнологии (Лубенцова, Пиотровский, 2017), но не в экологии. Эта тема ждет своего развития в нашей области.

Заключение или выводы

1. С помощью метода Заде – Мамдани можно создавать математические правила классификации биологических объектов, в частности диагностику пола животных.

2. Средствами R несложно создать программу, осуществляющую полный цикл расчетов – ввод эмпирических данных, построение функций принадлежности, расчет продукционных правил, расчет модельного прогноза (характеристики статуса объекта).

3. Построенная модель прижизненной диагностики пола обыкновенной гадюки по окраске тела, размерам хвоста и тела обеспечивает определение пола в 90 % случаев, что нельзя признать удовлетворительным; следует расширить набор характеристик.

4. Очевидным преимуществом рассмотренного алгоритма классификации является возможность использования признаков любого типа (качественных, счетных, пластических).

Библиография