Коросов А. В. О применении алгоритмов MaxEnt в экологии // Принципы экологии. 2024. № 1. С. 80–96. DOI: 10.15393/j1.art.2024.14742

Выпуск № 1

Методы экологических исследований

pdf-версия статьи

57.087.1:519.2

О применении алгоритмов MaxEnt в экологии

Введение

В последнее время получила широкое распространение программа Maxent, позволяющая строить модели пространственного распространения (Species distribution models) отдельных видов животных и растений, SDM-модели (Шитиков, 2020). Программа представлена в свободном доступе (Maxent…, 2023), руководство к этой программе изложено как на английском, так и на русском языках (Phillips, 2009; Краткое введение в MaxEnt, 2013). Теоретические основы изложены с статье J. Phillips and M. Dudik (2008), есть и перевод (Теоретические основы…, 2013). Обсуждению эффективности этой программы посвящена серия публикаций (Лисовский, Дудов, 2020; Шитиков и др., 2021 и пр.). По существу, программа MaxEnt позволяет рассчитать вероятность встречи того или иного вида животных в разных точках пространства, ориентируясь на распространение значимых для этого вида экологических факторов, т.е. реконструировать видовые ареалы.

Анализируя опыт использования этой программы по отношению к животным, можно увидеть как завышенные ожидания (Некрасова, Титар, 2014), так и избыточную критику (Черлин, 2020). Источником этого видится недопонимание отдельными авторами существа метода максимальной энтропии (ММЭ), положенного в основу программы MaxEnt (Maximum Entropy). Программный продукт MaxEnt реализует множество процедур обработки данных (ввод-вывод, статистическая обработка-иллюстрации и пр.), тогда как собственно метод максимальной энтропии по сути представлен одним блоком, который «лишь» высчитывает критерий успешности подбора модельных параметров. Предметом нашего рассмотрения служит логика и технология построения такого классификатора.

Во многих источниках во введении к содержательной части можно найти краткое выражение сути ММЭ, например: «...производится максимизация энтропии в пространстве, т.е. проводится поиск наиболее равномерного географического распределения предсказанного присутствия вида» (Лисовский, Дудов, 2020), или «...из всех возможных распределений вероятностей, при известных ограничениях, распределение с наибольшей энтропией наилучшим образом представляет моделируемые данные» (Шитиков и др., 2021), или «...among all probability distributions satisfying the constraints, we choose the one of maximum entropy, i.e. the most unconstrained one» (Phillips, Dudik, 2008), а также поясняющие его формулы:

Такое конспективное пояснение недостаточно для полноценного использования метода в экологических исследованиях. Необходимо глубже понимать смысл процесса и его ограничения, чтобы это знание предостерегло от неточностей в изложении результатов анализа. На наш взгляд, для формирования понимания этой идеи и соответствующих математических процедур следует конкретизировать все расчеты до уровня числа, начиная с самых простых примеров. Один из возможных вариантов объяснения этого метода реализован в среде MS Excel (Maximum-Entropy…, 2010). Мы попытались расширить понятийную часть и поспособствовать популяризации этого метода построения классификаций среди специалистов в области биологии и экологии.

Цель сообщения состоит в объяснении работы метода максимальной энтропии на серии усложняющихся числовых примеров из экологии. Все расчеты выполнены в среде R (The R…, 2023). Данные для приведенных скриптов загружаются по гиперссылке.

В разделе «Традиционные методы» на примерах поясняется собственно принцип максимальной энтропии. В разделе «Оригинальные методы» рассмотрены процедуры программы MaxEnt, выполняющие классификацию биологических объектов по их количественным характеристикам.

Материалы

Данные по морфологии обыкновенной гадюки, использованные во втором примере, были собраны по стандартным методикам на островах Кижского архипелага Онежского озера (Карелия) в 1991–2023 гг., оформлены в базу данных и частично опубликованы (Коросов, 2010).

Традиционные методы исследований

Метод максимальной энтропии используется в процедуре подгонки модели под реальность, качество которой оценивается по величине энтропии. «Найти параметр распределения p, при котором энтропия распределения максимальна (при известных внешних ограничениях)» – вот краткая формулировка этого метода (Джейнс, 1982; Белашев, Сулейманов, 2002; Philips et al., 2006). Рассмотрим входящие в нее термины.

Распределение – это соотношение между значениями признака (y) и частотой их встречаемости (a) (Иванова и др., 1981). Так, в нашем примере изучается альтернативное распределение, которое имеет всего два значения, два класса объектов, – совокупность особей обыкновенной гадюки, составленная из 373 взрослых самок и 229 самцов: k = 2, y = 0 и y = 1, a_(y=0) = 373, a_(y=1) = 229. Другие виды распределения имеют большее число классов, k > 2. Обычно распределение задают как соотношение между значениями из i-го класса и относительной частотой (вероятностью) его встречи, как серию значений p_i. Параметр p_i вычисляется как доля объектов в каждом классе от общего объема выборки, p_i = a_i/n. Обычно вероятности разных значений (классов) не равны: p₁ ≠ p₂ … ≠ p_i … ≠ p_k, их сумма равна единице Σp_i = 1. Так, p_(y=0) = 373/603 = 0.62; p_(y=1) = 0.38.

Энтропия – это мера разнообразия возможных состояний, мера неопределенности исхода эксперимента (Экоинформатика, 1992; Энтропия…, 2022). Здесь рассматривается не физический, а информационный смысл термина. Каждый эксперимент может закончиться по-разному (то ли появится A, то ли появится B). Если вероятности разных исходов наблюдений равны (такое распределение называется равномерным), то энтропия принимает свое максимальное значение, равное E = log(k), где k – число возможных исходов. Так, для альтернативного распределения (в котором есть всего два типа значений k = 2) неопределенность составит ln(2) = 0.693 или log₂(2) = 1 (один бит). Когда же вероятности разных исходов не равны, неопределенность (энтропия) рассчитывается по формуле К. Шеннона: E = – Σ(p_i*log(p_i)). Для нашего альтернативного распределения энтропия составит:

E = –(p₀ * ln(p₀) + p₁ * ln(p₁)) = –(0.62 * log(0.62) + 0.38 * log(0.38)) = –(0.296 – 0.368) = 0.664,

что меньше, чем при полной выравненности ln(2) = 0.693.

Ограничения – условия формирования вероятности p_i. В первой задаче таких условий нет, во второй задаче вероятность «быть самцом» определяется морфологическим обликом особей (представленным в промерах).

Итак, максимальное значение E_max = log(k) энтропия обретает в том случае, когда вероятности ожидаемых событий равны: p₁ = p₂ = p_i = … = p_k , т.е. при равномерном распределении.

 ***

Задача 1: использовать метод максимальной энтропии для оценки параметров простого распределения с семью равновероятными исходами.

Нужно найти вероятности распределения p₁ = p₂ = p_i = … = p_k (k = 7), для которого наблюдается максимум энтропии E → max (т.е. параметр p_i равномерного распределения).

Сразу понятно, что условие выполняется при p_i = 1/7 = 0.1428571. Однако в следующей задаче значения p_i будут зависеть от характеристик самого объекта и внешних факторов. Следовательно, сначала нужно ознакомиться с алгоритмом перебора значений p_i в стремлении найти тот вариант, когда энтропия максимальна, т.е. все вероятности равны друг другу.

Первый технический момент состоит в том, что подбор параметров будет выполняться с помощью алгоритма оптимизации, значит, нужна формула для расчета невязки. При подгонке параметров требуется максимизировать значение E. Однако такие функции оптимизации среды R, как nlm() или optim(), призваны минимизировать невязку, сводить ее к нулю. Превратить задачу максимизации в задачу обнуления можно, если определить невязку как положительную разность между максимальным значением энтропии E_max и промежуточными значениям энтропии E_j, получаемым в процессе настройки. Энтропия имеет максимальное значение при полной выравненности распределения и равна полной неопределенности исхода E_max = ln(n). Текущее значение энтропии при исходных значениях p будет отрицательным E = –Σ(p_i * log(p_i)). Следовательно, всегда положительная невязка, подлежащая обнулению, будет равна ln(n) + Σ(p_i * ln(p_i)) (хотя достичь нуля практически никогда не удается).

Второй момент связан с сохранением условия Σp_i = 1, поскольку изучается одно распределение, для которого какое-нибудь отдельное событие из полной группы событий обязательно случится. Это условие приходится навязывать процедуре оптимизации (нормировать p_i на сумму). Стартовое (случайное) распределение вероятностей зададим формулой: p1<-s/sum(s) (s – случайные числа); промежуточные значения будем рассчитывать как p2<-p/sum(p).

В скрипте в первой строке определяем пользовательскую функцию расчета невязки, исходя из принципа максимальной энтропии. Сначала происходит нормирование набора значений p_i на их сумму (p<-p/sum(p)), затем рассчитывается энтропия распределения sum(p*log(p)) и величина невязки log(n)+sum(p*log(p)). Далее в программе получаем первичный случайный ряд значений вероятностей (p1<-s/sum(s)). Затем вызываем функцию настройки f. Эта функция, перебирая разные значения p_i, стремится получить максимум энтропии и после ряда итераций дает распределение вероятностей, которое оказывается равномерным (p2), что хорошо видно на рис. 1.  

f<-function(p){p<-p/sum(p) ; return(log(n)+sum(p*log(p)))} n ← 7 ; s ← runif(n) ; p1 ← s/sum(s) sum(p1) plot(p1,type='h',ylim=c(0,.5),lwd=2) p←nlm(f,p1)$estimate ; p2←p/sum(p) lines(p2,col=2,lwd=2) legend("topright",legend=c(1,2), col=c(1,2), lwd=c(2,2)) p2 [1] 0.1420203 0.1410479 0.1443041 0.1432673 0.1444094 0.1442522 0.1406988 sd(p1) ; sd(p2) [1] 0.08978224 [1] 0.00159423 sum(p1*log(p1)) ; sum(p2*log(p2)) ; log(n) [1] -1.744039 [1] -1.945857 [1] 1.94591

 

Рис. 1. Случайные значения параметра p1 (1) и значения параметра p2 после настройки (2)

 Fig. 1. Random values of parameter p1 (1) and values of parameter p2 after setting (2)

 

По сравнению со стартовым рядом случайных чисел p1 новый ряд вероятностей p2 имеет почти предельно большое значение энтропии (1.94586 против 1.94591) и резко сниженную дисперсию (0.0016 против 0.0898). Новые значения вероятностей равны друг другу с точностью до сотых: p1[1]≈...≈p1[7]≈ 0.14.

Метод максимума энтропии долгое время использовался в математических и технических сферах, пока его не предложили для применения в биологии в качестве алгоритма описания ареалов животных и растений. С появлением удобной программы MaxEnt (Phillips, Dudik, 2008) он вошел в арсенал новых ценных методов биометрии.

Оригинальные методы исследований

Необходимость в применении метода максимальной энтропии возникает при существенном дефиците или неточности экологической информации (Лисовский, Дудов, 2020). Так, при изучении области распространения видов безусловным фактом можно считать только наличие вида (событие y = 1), тогда как отсутствие встречи вида в данной точке местности может быть вызвано как неподходящими для него условиями обитания (событие y = 0), так и отсутствием полевых наблюдений или ошибками при их проведении (вид есть, но не зарегистрирован). По этой причине для всех случаев ненаблюдения вида нельзя точно сказать, имело ли место событие y = 0. Таким образом, информация об условиях обитании вида оказывается однобокой, мы имеем характеристики лишь благоприятных местообитаний, которые лишены контраста, характеристик для альтернативы нет. Такая неполноценная односторонняя информация не позволяет рассчитать области обитания вида с помощью традиционных методов «классификации с обучением» (регрессионные, дискриминантные, нейросетевые…), для которых необходима тренировочная выборка из серии объектов с точно известным качеством двух типов (y = 0 и y = 1).

Метод максимальной энтропии меняет логику подхода: для него достаточно выборки точно установленных объектов одного качества (y = 1). С его помощью строится модель, максимально унифицирующая, выравнивающая объекты по статусу, по их свойству «быть объектами y = 1». В конечном итоге модель позволяет разделить выборки на «объекты y = 1» и «объекты не y = 1», которые можно считать «объектами y = 0».

Для уяснения сути метода максимальной энтропии мы взяли проблему, не связанную с оценкой ареалов. Возможно, смена задачи позволит читателям с другой стороны посмотреть на интерпретацию результатов работы программы MaxEnt.

 ***

Задача 2: определить пол гадюк по размерным показателям (x).

Используя характеристики особей, предстоит найти формулу для расчета вероятности «быть самцом», с помощью которой можно, во-первых, надежно определить особей первой группы как самцов, во-вторых, оценить вероятность принадлежности каких-либо особей второй группы к самцам, если они там есть. Понятно, что особи «не самцы» будут самками. Модель должна выражать зависимость вероятности q «быть самцом» (y = 1) от морфологических характеристик x:

q_i(y = 1) ~ F(x_i, a),

где q – вероятность i-го события y_i = 1 (самец) среди таких же событий в данной выборке, F – функция связи между переменными, x_i – морфологические характеристики особи, соответствующие событию y = 1 , a – параметры модели.

Величину q можно воспринимать как индекс пола, основанный на соотношении промеров; подобные индексы, разделяющие особей разного статуса (пол, возраст, вид), широко распространены в экологии животных.

Наша выборка включает несколько (N = 20) особей гадюки, разделенных на две группы. В первую вошли n = 10 самцов, во вторую ‒ еще 10 особей, возможно, разнополых. У змей описана окраска спины (номера 7 категории: Grey, Dark, Melanist, Black, Cyan, Light, Salad) x1, измерена длина хвоста x2, длина тела x3, масса тела x4. Для придания результатам большей определенности для примера подобрали только взрослых гадюк с длиной тела от 50 до 55 см. Можно сразу указать на признаки, достаточно хорошо выделяющие самцов гадюки, ‒ это обычно светлый фон спины (коды 1, 2, 3, 5) и относительно длинный хвост.

Поскольку в дальнейшем предстоят логарифмические операции и сравнение вклада разных показателей в диагностику пола, все характеристики необходимо трансформировать в безразмерные «функции предикторов» (features) f(x) (Phillips et al., 2006), что можно сделать разными способами (Лисовский, Дудов, 2020). Мы привели данные по гадюкам к величинам из диапазона от 0 (минимальный промер) до 1 (максимальный промер) по формуле: f(x_i) = (x_i ‒ x_min)/(x_max ‒ x_min). Важно отметить, что шкалирование выполняется для всех N = 20 особей исходной выборки (max и min определялись по всей выборке), поскольку в конечном итоге вероятность «быть самцом» (q_i) будет рассчитываться для всех особей.

Теперь можно конкретизировать формулу для нашего случая:

q_i ~ a1 f(x1_i) + a2 f(x2_i) + a3 f(x3_i) + a4 f(x4_i),

где q_i ‒ вероятность для i-й особи быть самцом; a ‒ коэффициенты пропорциональности; f(x_i) ‒ шкалированные значения исходных характеристик x_i; ~ ‒ знак, обозначающий форму зависимости между переменными, которая будет обсуждаться ниже.

Рассмотрим, какой смысл вкладывается в величину q_i в алгоритме MaxEnt. Значение q_i оценивает вероятность каждой особи быть самцом в пределах класса «самцы» (y = 1), точнее, это доля от общей вероятности для группы из n самцов, приходящаяся на одну особь. Сумма всех этих значений устанавливается равной единице Σq_i = 1. На первый взгляд кажется очевидным, что для любой особи эта величина будет равна q_i = 1/n, поскольку в группе из n самцов каждая особь ‒ самец, имеющий одну и ту же вероятность быть самцом. Однако задача поставлена так, чтобы дать заключение, является ли данная особь самцом, ориентируясь не на половые, а на пластические морфологические признаки, на промеры. В этом смысле самцы несколько отличаются друг от друга, имеют разную степень «самцовости» («брутальности»), хотя все вместе явно отличаются от самок. Величина q_i призвана выразить степень «самцовости» по размерным признакам, предположительно связанными с полом.

Идеальным можно считать случай, когда каждый самец получил бы одно и то же значение (индекс) «самцовости» q_i, а каждая самка получила бы другое значение, отличное от самцового. Поскольку о самках по условию задачи нам ничего неизвестно, остается отыскивать такое значение q_i, к которому будут тяготеть все изучаемые самцы (первая группа). Иными словами, нужно построить такую модель, расчеты по которой для каждого самца будут давать как можно более близкие значения q_i.

Величина q_i зависит как от значений промеров x, так и от величины коэффициентов пропорциональности a. Следовательно, необходимо подобрать такие значения коэффициентов a, чтобы расчетные значения q_i для всех самцов были как можно более близкими. Поскольку величины q_i представляют собой доли, в сумме дающие единицу, для них можно рассчитать метрику выравненности, энтропию, по формуле Шеннона (см. выше). При наибольшей близости всех значений q_i энтропия будет максимальной.

В этом и состоит принцип максимума энтропии применительно к нашей задаче: найти такие значения параметров a, при которых энтропия распределения q_i  примет наибольшее значение E→max.

Теперь необходимо определиться с конкретной формой зависимости вероятности «быть самцом среди других самцов» от размерных признаков. Не вдаваясь в детали теории вероятностей и математической физики, приведем рабочую формулу для расчета q_i (Phillips, Dudík, 2008):

,

где q – вероятность быть самцом, λ – коэффициенты пропорциональности, f(x) – шкалированные значения переменных x, k – число переменных (i = 1, 2, …, k), Z – значение для нормирования частных значений q_i , чтобы в сумме они давали единицу; по факту, это просто сумма всех значений q_i , рассчитанных для всех n особей (j = 1, 2, …, n):

 .

В результате расчетов для каждого самца будем получать значения q_i, сумма которых равна единице.

Приведенная формула описывает экспоненциальное распределению Гиббса, которое используется в статистической физике для характеристики распределения микросостояний объектов (Ансельм, 1973). Почему же мы можем принять, что вероятность «быть самцом» будет подчиняться экспоненциальному закону? В силу отличия самцов друг от друга распределение q_i не будет равномерным, но резко асимметричным: большинство особей действительно будут довольно близки друг к другу, хотя малая часть особенно «брутальных» самцов будет отличаться от остальных.

Запишем эту формулу для нашего случая:

 .

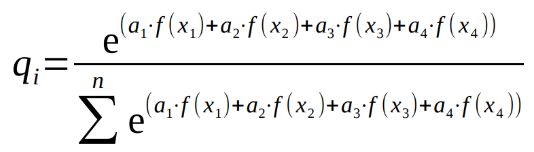В формате программы R формула примет следующий вид (для самцов mn<-1:10):

suv<-exp(a[1]*v[mn,1]+a[2]*v[mn,2]+a[3]*v[mn,3]+a[4]*v[mn,4]) q<-suv/sum(suv)

Перед составлением программы расчетов нужно отметить один нюанс. Значения характеристик x преобразуются к диапазону 0÷1 безразмерной вкличины v для всех N = 20 особей исходной выборки. Однако значения вероятности q_i нормируются и выравниваются только для выборки первых десяти особей (самцов).

* * *

Итак, у нас есть вся информация для составления скрипта модели.

Вначале создаем пользовательскую функцию fu, чтобы рассчитывать значения q распределения Гиббса, значения его  энтропии sum(q*log(q) для всех особей и значения невязки log(20)+sum(q[nm]*log(q[nm])) только для самцов.

fu<-function(a) { suv<-exp(a[1]*v[,1]+a[2]*v[,2]+a[3]*v[,3]+a[4]*v[,4]) q<-suv/sum(suv) return(log(20)+sum(q[nm]*log(q[nm]))) }

Затем из файла загружаем массив данных для 10 самцов и 10 других особей (индекс цвета – col, длина хвоста – lc, длина тела – lt, масса – w, индекс пола – s). ("vipmor_10.csv")

head(x<-read.csv("vipmor_10.csv" )[-1],3) col   lc    lt     w  s 1 1 80 52.0  92  1 2 1 80 51.0  85  1 3 3 90 50.5 100 1

Далее задаем размеры выборок и преобразуем исходные значения переменных x в безразмерные величины v.

N<-nrow(x) ; n←10 ; f←10 nm←1:n ; nf←(n+1):(n+f) ; nmf←c(nm,nf) v<-data.frame(col=rep(0,N),lc=rep(0,N),lt=rep(0,N),w=rep(0,N)) v[1]<-(x[,1]-min(x[,1]))/(max(x[,1])-min(x[,1])) v[2]<-(x[,2]-min(x[,2]))/(max(x[,2])-min(x[,2])) v[3]<-(x[,3]-min(x[,3]))/(max(x[,3])-min(x[,3])) v[4]<-(x[,4]-min(x[,4]))/(max(x[,4])-min(x[,4])) head(v,3)                col         lc              lt              w 1 0.3333333 0.7500 0.4285714 0.0000000 2 0.1666667 0.6875 0.1428571 0.1428571 3 0.0000000 0.7500 0.7142857 0.7959184

 Выводим исходные данные на диаграмму (рис. 2).

matplot(v[nmf,c(1:4)],pch=c(1:4),col=1,xlim=c(1,24)) legend('topright',legend=c(1:4),pch=c(1:4))

 

  

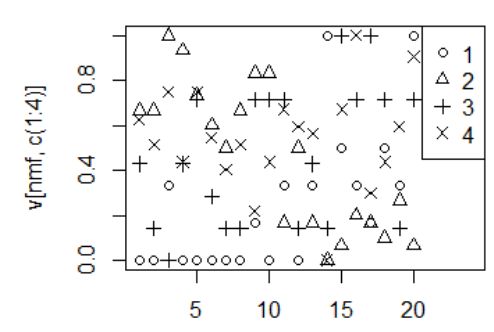
 Рис. 2. Приведенные к диапазону 0÷1 значения индекса окраски (1), длины хвоста (2), длины тела (3), массы тела (4) для самцов (первые 10 значений) и прочих особей (11‒20)

Fig. 2. The values of the coloration index (1), tail length (2), body length (3), body weight (4) for males (the first 10 values) and other individuals (11–20) reduced to the range 0÷1

 

Можно заметить, что самцы, как правило, имеют минимальные значения индекса окраски (1) и высокие значения длины хвоста (2), по остальным признакам разнополые особи неразличимы.

 Далее задаем случайные стартовые значения параметров a1.

(a1<-runif(4)) [1] 0.7268095 0.7427056 0.9009481 0.1611613

Используя функцию fu и случайные параметры a1, выполняем настройку модели с помощью функции оптимизации модифицированным методом Ньютона: подбираются такие значения коэффициентов a2, чтобы обнулить функцию невязки fu.

opa<-optim(a1, fu, method = "L-BFGS-B") (a2<-opa$par) [1] -3.829332 4.268631 -1.233534 -1.449245

Далее рассчитываем значения вероятностей q1 с использованием исходных значений параметров a1 и значения вероятностей q2 с использованием настроенных значений параметров a2.

suv<-a1[1]*v[,1]+a1[2]*v[,2]+a1[3]*v[,3]+a1[4]*v[,4] q1<-exp(suv) ; q1<-q1/sum(q1) suv<-a2[1]*v[,1]+a2[2]*v[,2]+a2[3]*v[,3]+a2[4]*v[,4] q2<-exp(suv) ; q2<-q2/sum(q2) miq<-min(q2) ; maq<-max(q2)

Теперь строим диаграмму (рис. 3), выражающую соотношение между самцами и самками по значениям вероятности q, а также рассчитываем стандартные отклонения и величину энтропии для распределения q1 и q2.

plot(q1[(nmf)],xlim=c(1,22),ylim=c(miq,maq),pch=x[,5], xlab=c('m                     f')) points(nm,q2[nm],col=2, pch=16) points(nf,q2[nf],col=4, pch=15) legend('topright',legend=c(1:4),pch=c(1,16,0,15),col=c(1,2,1,4)) #-------------------------------- print(c(sd(q1[nm]), sd(q2[nm])),4) [1] 0.009525 0.039428 print(c(log(n), -sum(q1[nm]*log(q1[nm])), -sum(q2[nm]*log(q2[nm]))),4) [1] 2.303 1.384 2.132

 

 Рис. 3. Значение вероятности q для изучаемых самцов (1, 2) и прочих особей (3, 4) до (1, 3) и после (2, 4) настройки параметров a

Fig. 3. The probability value q for the studied males (1, 2) and other individuals (3, 4) before (1, 3) and after (2, 4) parameter settings a

 

Отображенные на диаграмме (см. рис. 3) результаты ясно показывает, что с исходным значениями параметров a1 (0.9706960 0.4910060 0.2369080 0.4903713) рассчитанные значения q1 не позволяют выделить самцов среди всех особей выборки. После настройки значения параметров a2 сильно изменились (–3.63407654 3.44157111 –0.68394084 –0.04437958). Как и ожидалось, выделяются веса для индекса окраски (‒3.6) и длины хвоста (3.4). Значения q2 для конкретной особи тем больше, чем у нее меньше индекс окраски и длиннее хвост, т.е. у самцов. Остальные параметры стремятся просто снизить значения ненужных показателей. В результате облако точек для самцов оказалось расположено существенно выше облака для особей с неизвестным полом. Однако одна точка (особь 12) оторвалась от второй группы и приняла значение, неотличимое от самцов. Поскольку мы все же знаем реальный пол особей в выборке, то можем сказать, что особь 12 ‒ это и есть один самец среди самок второй группы.

При этом величина энтропии после настройки существенно увеличилась с 1.384 до 2.132, хотя и не достигла своего максимума ln(10) = 2.303.

Для более рельефного отображения результатов моделирования значения q, которые выражают «вероятность быть самцом среди других самцов», можно превратить в величину p «вероятность быть самцом». Между ними имеется криволинейная зависимость, которая описывается уравнением логистической регрессии (Phillips, Dudik, 2008):

p(y = 1|x) = e^Hq(x)/(1 + e^Hq(x)),

где H ‒ энтропия распределения q(x) для тех или иных значений прометров (x) всех особей выборки.

В программе мы оформили этот расчет и построение диаграммы как отдельную функцию (plof). Сначала рассчитывается энтропия H<--sum(qq*log(qq)), затем значения вероятности «быть самцом» pp<‑exp(H)*qq/(1+exp(H)*qq), которые далее выводятся на диаграмму (рис. 4).

plof<-function(qq,le){ H<--sum(qq*log(qq)) p<-exp(H)*qq/(1+exp(H)*qq) np<-data.frame(p,x[,5]) #---------------------------------- plot(np[,1],type='n', xlim=c(1,N),ylim=c(0,1)) text(np[,1],lab=np[,2],col=1) abline(h=le) legend('topright',legend=c(1,0)) } plof(q1,.5) plof(q2,.5)

 

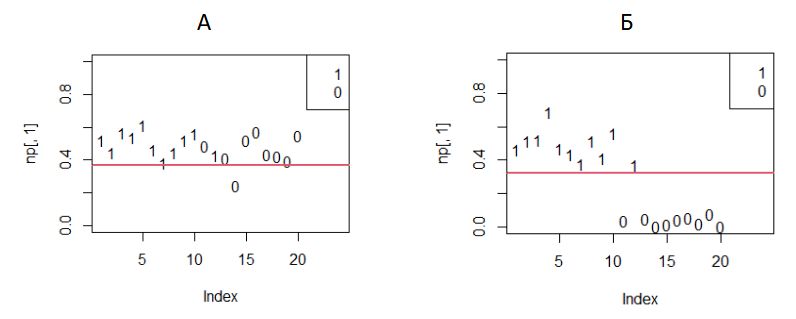
 Рис. 4. Вероятность «быть самцом» до (А) и после (Б) настройки параметров модели: 1 ‒ самцы, 0 ‒ самки

 Fig. 4. The probability of "being a male" before (A) and after (Б) setting the model parameters: 1 ‒ males, 0 ‒ females

 

На диаграмме достаточно хорошо видно, что когда параметры модели вначале имеют случайные значения (a1), самцы и самки неразличимо перемешаны. После настройки модели по критерию максимальной энтропии разнополые особи отчетливо разделяются.

Таким образом, модель не только позволила отделить особей, исходно заданных как самцы, но и по морфологическим признакам определить пол неизвестной особи. Иными словами, принцип максимума энтропии позволяет правильно настраивать модели классификации с использованием односторонней неполной информации.

Обсуждение

В соответствии с заявленными целями мы рассмотрели процедуру построения классификационной модели с использованием принципа максимальной энтропии, которая в деталях отличается от алгоритма, реализованного в программе MaxEnt (Maximum…, 2010; Краткое введение…, 2013). Тем не менее попытка решить эту задачу в среде MS Excel по точному алгоритму MaxEnt, представленному в Интернете (Maximum…, 2010), дала такие же результаты: первый десяток и еще особь 12 были идентифицированы как самцы.

Это позволяет считать наш алгоритм работоспособным и в его рамках обсудить важный вопрос о назначении границы, отделяющей самцов от самок, т.е. проблему назначения порога бинаризации прогноза (точки отсечения, cut-point, сp). Собственно к методу MaxEnt этот вопрос не относится, поскольку проблема назначения границ по-своему решается разными методами классификации. Однако важно обсудить, как эта задача решается на результатах применения методов максимальной энтропии.

Чему должна быть равна вероятность p, чтобы особь «была самцом»? Казалось бы, вероятность должна быть выше 0.5, поскольку в типичной популяции соотношение полов близко к паритету. Тем не менее результаты анализа показывают (рис. 4, 5), что облако точек для самцов располагается выше линии p = 0.3, а не p = 0.5. На это есть свои причины, обсуждение которых увело бы нас в сторону от основной темы. Проблеме поиска границы, разделяющую события y = 1 и y = 0 методом MaxEnt, посвящено много публикаций (см.: Schisterman et al., 2005; Лисовский, Дудов, 2020). Рассмотрим некоторые пути разрешения проблемы.

 

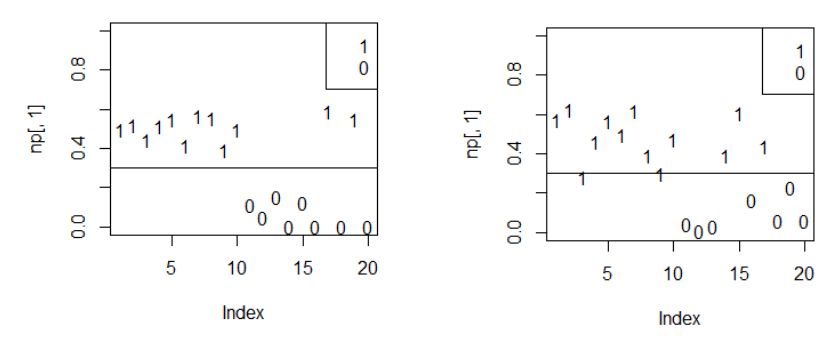
 Рис. 5. Вероятность «быть самцом» для разных случайных выборок; 1 – самцы, 0 – самки

Fig. 5. The probability of "being a male" for different random samples; 1 – males, 0 – females

 

Одним из вариантов поиска классификационного порога является ROC-анализ (Шитиков, Мастицкий, 2017; Беляев и др., 2023). Он состоит в переборе всех возможных значений порога – от 0 до 1 (с шагом 0.1, 0.01 или другим) в стремлении найти лучший. На каждом шаге назначается все увеличивающееся значение порога и текущее значение используется для разделения объектов (особей) на две группы. Если для данной особи текущее значение вероятности «быть самцом» выше порога p_i > cp, особь попадает в группу самцов (y = 1), если ниже – в группу прочих (y = 0). Далее на этом шаге по всем особям рассчитываются две величины: а) доля правильно рассчитанных значений y = 1 (показатель называется чувствительность, sensitivity, se) и б) доля правильно рассчитанных значений y = 0 (показатель называется специфичность, specificity, sp). Эти величины (se, sp) позволяют построить графики их зависимости от значений порога (cp) (рис. 6). Точка пересечения графиков рассматривается как выполнение требования баланса между чувствительностью и специфичностью (Логистическая регрессия..., 2020; Беляев и др., 2023), соответствующее ей значение cp принимается как оптимальная точка отсечения. Для численного определения этого значения служит индекс Юдена, смысл которого состоит в том, что на ROC-кривой эта точка максимально удалена от главной диагонали: сp_opt = maximum{se + sp – 1} (Schisterman et al., 2005; Беляев и др., 2023).

Рассмотрим скрипт для определения оптимально сбалансированного порога бинаризации. В качестве данных возьмем выборку из 150 самцов и 150 прочих особей. К этому этапу уже рассчитаны и записаны в файл ('s_p_300_samples.csv') значения вероятности быть самцом p_i для каждой особи с известным полом s_i. После загрузки данных выполняется подсчет, сколько реальных самцов (n1) и самок (n0) находится в выборке. Далее задаем число шагов вычислений steps=100; размеры массивов se, sp. Определяем значения серии возможных точек отсечения сp<-seq(0,1,length out=steps). Организуем цикл расчетов для каждого порога бинаризации (100 шагов).

steps<-100 (cp<-seq(0,1,length.out=steps)) sp<-read.csv('s_p_for_300_samples.csv') s<-sp[,1] ; p<-sp[,2] (n1<-sum(s==1)) (n0=N-n1) se<-sp<-rep(0,steps) #---------------------------------- for (i in 1:steps){ y1<-which(p>cp[i]) y11<-sum(s[y1]==1) (se[i]<-y11/n1) y0<-which(p<cp[i]) y00<-sum(s[y0]==0) (sp[i]<-y00/n0) } (ocp<-cp[which((se+sp-1)==max(se+sp-1))]) #---------------------------------- plot(cp,se,type='l', lwd=3,,ylab='se, sp') lines(cp,sp,type='l',lty=2, lwd=2) abline(v=ocp[3]) legend("right",legend=c(1,2,3),lty=c(1,2,1),lwd=c(3,2,1),col=c('grey',1,1))

 Рассчитываем чувствительность se. Особь включается в список c положительными оценками y = 1, если значение p_i превысило очередной порог, cp.: y1<-which(p>cp[i]). Например, для cp[1]=0 все особи стали «самцами». Далее определяем, сколько особей из этого списка действительно являются самцами: y11<-sum(s[y1]==1), после чего вычисляем долю правильно положительно определенных самцов среди самцов se[i]<-y11/n1.

Рассчитываем специфичности sp. Особь включается в список c положительными оценками y = 0, если значение p_i было ниже текущего порога, cp.: y0<which(p<cp[i]). Для порога сp[1]=0 ни одна особь не получила статуса «самка». Далее определяем, сколько особей из этого списка действительно являются самками: y00<-sum(s[y0]==0), после чего вычисляем долю правильно положительно определенных самок среди реальных самок sp[i]<-y00/n0.

Полученные ряды se и sp наносим на график (рис. 6), отыскиваем точку пересечения, опускаем нормаль и визуально определяем сбалансированное значение точки отсечения. Для точного расчета лучшего сбалансированного значения точки отсечения находим ряд значений se+sp-1, а среди них – максимальное значение. В примере оказалось, что таких значений четыре: 0.15, 0.16, 0.17, 0.18. На диаграмму нанесено третье.

(ocp<-cp[which((se+sp-1)==max(se+sp-1))]) [1] 0.1515152 0.1616162 0.1717172 0.1818182

 

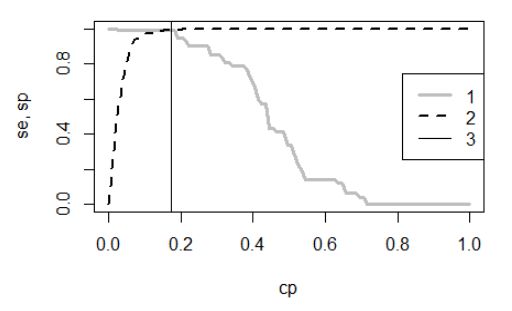
 Рис. 6. Графики Чувствительности (1) и Специфичности (2) модели для разных значений точки отсечения (cp); вертикальная линия (3) проведена из точки пересечения графиков и соответствует значению cp = 0.17

Fig. 6. Graphs of Sensitivity (1) and Specificity (2) of the model for different values of the cut-off point (cp); a vertical line (3) is drawn from the intersection point of the graphs and corresponds to the value cp = 0.17

 

При всей строгости анализа применение этой логики в рамках метода MaxEnt имеет существенный изъян. В нашем примере мы точно знаем число объектов разного качества n1 и n0. Обычно же (по условиям задачи) информация ограничена: нам известно только, что серия объектов обучающей выборки (объемом n) принадлежит к группе y = 1. Таким образом, мы можем рассчитать только «чувствительность», долю правильно рассчитанных значений y = 1 относительно этой группы. Однако у нас нет информации о том, какие объекты второй группе наверняка имеют статус y = 0. Следовательно, мы не можем рассчитать «специфичность», долю правильно рассчитанных значений y = 0, не можем корректно выполнить ROC-анализ, не можем точно определить порог бинаризации. Конечно, у исследователя всегда есть представление о том, что определенные объекты, «видимо», принадлежат к классу y = 0. Кроме того, оценки отсутствующих встреч можно подменить косвенными показателями, например расчетами соотношения обследованной площади и той, где объекты встречались (Phillips, 2009; Краткое введение…, 2013). Однако все равно это будет лишь приблизительная информация. Любые оценки точки отсечения на таких данных должны будут сопровождаться эпитетом «видимо». Правда, судя по литературе, почти никто из авторов, применяющих MaxEnt на практике, не затрудняется делать такую оговорку, считая алгоритм программы MaxEnt непогрешимым.

Иногда для программы MaxEnt рекомендуют брать «механический» порог 10 процентилей; в случае анализа размещения видов это значит, что лишь «90 % точек присутствия, включенных в анализ, попадают в "потенциальный ареал"» (Олонова, Гудкова, 2017, с. 40). Для нашего случая это означает, что 10 % самцов не нужно считать самцами. Для первого примера (см. рис. 4 Б) 10 % – это одна особь с наименьшим значением p = 0.38, т.е. граница составит cp = 0.39. Для задачи определения пола введение такого порога кажется странным, поскольку пол определялся точно по первичным и вторичным признакам, и в том, что перед нами самец, сомнения нет. Более логичным кажется (чтобы избежать исключения кого бы то ни было) назначать пороговый уровень бинаризации, равным минимальному значению p, выше которого расположены все самцы, формирующие обучающую выборку; тогда граница будет равна cp = 0.30. В то же время назначение столь важной границы по величине интервала ограниченной группы объектов выглядит несерьезно, ведь морфологическое разнообразие реальных объектов (самцов) может быть больше, чем в изучаемой обучающей выборке. Очевидно, нужен какой-то статистический показатель, корректно экстраполирующий свойства выборки на свойства генеральной совокупности, т.е. статистический прием для назначения точки разрыва.

В качестве такой величины можно рассмотреть границы доверительного интервала. В процессе настройки модели алгоритм стремится выровнять значения p_i для обучающей выборки самцов так, чтобы рассчитанная по ним энтропия стала максимальной. Процедура выравнивания значений p_i обычно не может свести их к одной величине, но вполне может ликвидировать избыточную изменчивость (нивелировать сильно отклоняющиеся варианты) и обеспечить более или менее симметричное распределение, близкое к нормальному (в примере уже для 150 особей гистограмма стала симметричной, рис. 7). Это значит, что в качестве критических границ можно взять не процентиль от размаха, а квантиль от распределения. Квантиль p = 0.975 традиционно используется в биометрии для построения доверительных интервалов и составляет удвоенное стандартное отклонение от средней. Исходя из этого получаем формулу расчета порога бинаризации для p = 0.95: cp_opt = M_q(y=1) – 2*S_q(y=1), или в формате R: cp<-mean(p[mn])-2*sd(p[mn]), где mn = 150 – число реальных самцов в обучающей выборке.

 
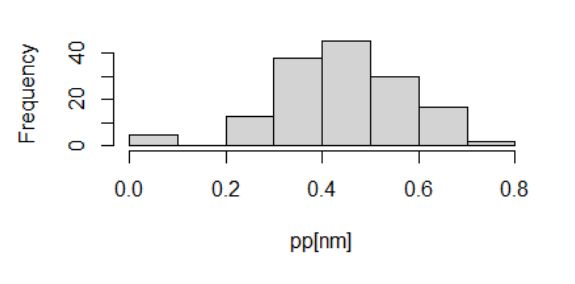 Рис. 7. Распределение значений вероятности «быть самцом» для 150 самцов обучающей выборки (см. рис. 8Б)

Fig. 7. Distribution of the probability values of "being a male" for 150 males of the training sample (see Fig. 8Б)

 

Для нашего примера (mean(qm) = 0.4446, sd(qm) = 0.1335) значение точки отсечения cp_q=0.975 = 0.1775, рассчитанное как нижняя граница доверительного интервала, практически совпало со значением индекса Юдена, рассчитанным при выполнении ROC-анлиза (с точным знанием о статусе всех объектов!).

На наш взгляд, квантильный индекс логически более уместен при использовании метода максимальной энтропии по той причине, что в его расчет включены характеристики только тех объектов, статус которых точно известен, и вместо неопределенных предположений о наличии объектов y = 0 можно пользоваться количественно заданными терминами «репрезентативность» и «доверительная вероятность» в отношении объектов с известным статусом y = 1. По простоте расчетов и прозрачному смыслу этот квантильный показатель порога cp лучше оценок, получаемых в ROC-анализе.

Эти соображения позволяют дополнить скрипт функции plof для вывода результатов.

plof<-function(qq){ H<--sum(qq*log(qq)) pp<-exp(H)*qq/(1+exp(H)*qq) np<-data.frame(pp,x[,5]) #---------------------------------- plot(np[,1],type='n', xlim=c(1,N),ylim=c(0,1)) text(np[,1],lab=np[,2],col=1) p<-(np[nm,1]) cp<-mean(p)-2*sd(p) abline(h=cp,col=2,lwd=2) legend('topright',legend=c(1,0)) } plof(q2)

 Как можно видеть на рис. 8, в разных прогонах полученная граница хорошо разделяет разнополых особей. При этом все же часть самцов оказалась за этой границей, т.е. должна быть идентифицирована как самки. Одна из возможных причин – незначительная редукция хвоста у самцов (из-за обморожения на зимовке), которая делает их неотличимыми от самок.

   

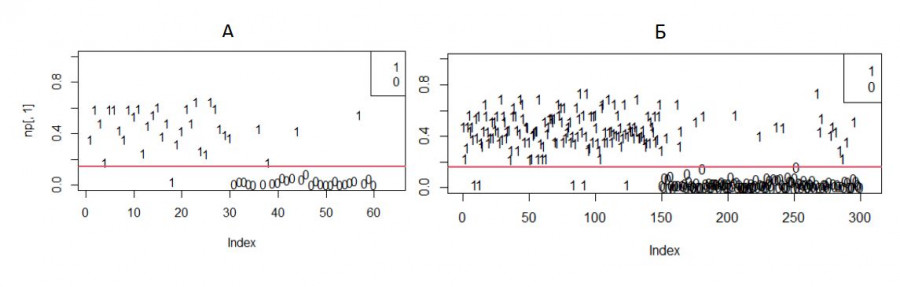
Рис. 8. Вероятность «быть самцом» для разных случайных выборок объемом 60 (А, 30 самцов и 30 прочих особей) и 300 (Б, 150 и 150); 1 – самцы, 0 – самки

Fig. 8. The probability of "being a male" for different random samples with a volume of 60 (A, 30 males and 30 other individuals) and 300 (Б, 150 and 150); 1 – males, 0 – females

Заключение или выводы

Подводя итоги изложенного, в первую очередь хочется отметить не вычислительные, а новаторские логические аспекты рассмотренного метода. Обычные методы классификаций объектов стремятся уловить контраст между разделяемыми группами. В технологии MaxEnt происходит лишь выявление (и усиление) феномена однообразия объектов одного статуса, и это автоматически приводит к отделению их от объектов другого статуса. Моделирование с помощью принципа максимума энтропии состоит в том, чтобы «выпятить» те свойства, которые делают изучаемую группу объектов единообразными, узнаваемыми, но в то же время «затушевать» другие, «банальные», свойства с неопределенной широкой изменчивостью. Как ни удивительно, этого оказывается достаточно, чтобы отсечь от изучаемых объектов все прочие, которые, следовательно, классифицируются как имеющие иной статус.

Оборотной стороной такой логики становится невозможность однозначной интерпретации результатов. Если альтернатива изучаемому классу (y = 1) явно не задана, всегда остается сомнение в справедливости полученного правила классификации, особенно в величине выбранного порога бинаризации. А что если набор изученных показателей не содержит подходящих характеристик для надежного разделения объектов по классам и их составы оказались не «чистыми»? Видимо, поэтому при анализе ареалов животных и растений обычно формируют огромный список всевозможных факторов влияния (и предлагают все новые) в надежде, что какие-нибудь из них да сработают. Несмотря на детальность и сложность процедур оценки значимости полученных коэффициентов, в классификационной модели в основе выводов всегда будет оговорка «видимо», поскольку предположение о статусе альтернативных объектов (y = 0) остается всего лишь предположением.

Принимая во внимание эти особенности моделирования с помощью принципа максимальной энтропии, остается рекомендовать читателям накапливать опыт по дифференциации биологически значимых разностей с затаенным восторгом от этой замечательной процедуры, классификации методом максимальной энтропии.

Библиография

Благодарности

Автор признателен В. В. Горбачу, С. В. Бугмырину и рецензентам за ценные замечания по улучшению текста.