Введение
Одним из важных процессов жизнедеятельности растительного организма является его водный обмен. Водный обмен растения – динамичный процесс, зависящий с одной стороны, от внутренних параметров растения, прежде всего, сопротивления движению воды и ее запасов в разных частях водопроводящей системы, с другой стороны – от факторов внешней среды. Исследованиям водного обмена растений разных экологических зон в широком диапазоне факторов среды посвящено множество работ (Kaipiainen et al., 1996; Sellin, 2001; Шереметьев, 2005; Сазонова и др., 2011; Bucci et al., 2012; Brodersen, McElrone, 2013; Сенькина, 2013; Scoffoni et al., 2014). Однако до сих пор остается открытым вопрос о возможных механизмах регуляции водного обмена на уровне целого растения, для выявления которых необходима информация о свойствах водопроводящей системы разных видов растений. В этой связи очевидный интерес представляют исследования водного режима древесных растений с аномалиями роста и развития. Уникальным экспериментальным объектом в этом плане являются растения березы повислой (Betula pendula Roth), особенностью которой является способность образовывать две формы: обычной березы повислой (Betula pendula Roth) с прямослойной древесиной и карельской березы (Betula pendula Roth var. carelica) с узорчатой древесиной. Вопрос о роли воздействия факторов среды на формирование структурных аномалий древесины и коры карельской березы широко обсуждается в литературе (Ермаков, 1986; Ветчинникова, 2004; Новицкая, 2008). В этом контексте изменения структурной организации тканей ствола, вероятно, должны влиять на обменные процессы, в частности, водный режим деревьев. Данное предположение требует дополнительных исследований параметров водообмена деревьев березы повислой с разной степенью выраженности признака узорчатости древесины.
Возможным вариантом для более глубокого анализа метаболического статуса растения и его адаптационных возможностей представляется моделирование биоритмов физиологических показателей в широком диапазоне внешних условий. Тренд сезонного мониторинга параметров водного режима позволяет предположить существование суточного ритма изменения этих величин с определенной амплитудой, периодом и сдвигом фазы относительно начала суток. Однако стохастическая природа данных требует применения вероятностных методов для анализа результатов, полученных в ходе наблюдения. Для этих целей в конце 60-х годов прошлого века была разработана процедура косинор-анализа (Хальберг, 1972; Багриновский и др., 1973). Этот метод предполагает, что если за нулевую точку ритмического тренда взять начало первых суток наблюдения (0 часов 0 минут), то в отсутствии других начальных условий для однозначного определения искомой ритмической кривой необходимо найти четыре параметра: амплитуду и частоту (период) колебания, акрофазу (сдвиг фазы относительно нулевой точки отсчета) и мезор (нулевой уровень, относительно которого происходит колебание). Для такого общего случая впоследствии была разработана циклическая расчетная процедура косинор-анализа, с помощью которой можно определить неизвестный период колебания и соответствующие ему остальные величины (Емельянов, 1976; Ашофф, 1982; Карп, 1989).
Целью нашего исследования была сравнительная оценка суточных ритмов водного потенциала облиственных побегов березы повислой (Betula pendula Roth) и карельской березы (Betula pendula Roth var. carelica (Merclin) Hämet Ahti) в вегетационной динамике с помощью косинор-анализа.
Материалы
Исследование проводили на экспериментальных участках Института леса Карельского научного центра РАН (ИЛ КарНЦ РАН) на территории Агробиологической станции КарНЦ РАН в окрестностях г. Петрозаводска (южная Карелия, 61045′N, 34020′Е). Объектами исследования служили 5-летние саженцы обычной березы повислой (Betula pendula Roth) с прямослойной древесиной и карельской березы (Betula pendula Roth var. сarelica) с узорчатой древесиной, произрастающие в одинаковых почвенно-климатических условиях (Сазонова и др., 2012).
Полевые исследования проводили в суточной динамике с интервалом в 3 часа с июня по сентябрь 2009 г. в дни с разными погодными условиями. Отбор образцов проводили в соответствии с фенологическим развитием деревьев рода Betula в фазы развертывания листьев, роста листьев и побегов, окончания интенсивного роста и осеннего расцвечивания листьев. В каждый срок отбор образцов проводили в 3-х биологических повторностях.
Методы
Водный потенциал (Ψ) в облиственных побегах определяли с помощью камеры давления Plant Moisture Vessel SKPM 1400 (Skye Instruments Ltd., Великобритания). Метеорологические параметры регистрировали с помощью системы LI-COR 6400ХТ (LI-COR Inc., США).
Для обработки результатов применяли методы описательной статистики (Гланц, 1999), автокорреляционного анализа, дисперсионного анализа ANOVA, а также процедуру одномерной линейной регрессии (Glantz, Slinker, 2003). Данные на графиках представляют средние значения из трех биологических повторностей. Проверку гипотез на статистическую достоверность различий и значимость рассчитанных статистик осуществляли при 5%-ном уровне значимости.
Подходы к статистической обработке временных рядов значений Ψ побегов берез. Предварительный статистический анализ временных рядов водного потенциала (Ψ) облиственных побегов березы повислой и карельской березы показал, что период колебательной компоненты тренда Ψ составил 24 часа. Мезор определили как линейную функцию, зависимую от времени вегетационного периода (месяц), параметры которой рассчитали методом наименьших квадратов отдельно перед использованием процедуры косинор-анализа. При этом единственными неизвестными параметрами биоритма остались амплитуда колебания и сдвиг фазы относительно нулевой точки отсчета (акрофаза).
Стандартная процедура косинор-анализа, реализованная в электронной таблице Excel (Шереметьев, 2005) и в среде R, предполагает неизвестными 3 параметра (мезор, амплитуду и акрофазу), при этом мезор считается константой. Решение задачи в этом случае происходит на основе квадратной матрицы 3х3. Оценив предварительно значение и сезонную динамику мезора, мы редуцировали матрицу до размера 2х2, что значительно упростило процедуру расчета амплитуды и акрофазы. Хотя такой подход не позволил использовать существующее программное обеспечение по косинор-анализу, он показался нам более естественным и отвечающим целям и задачам исследования, поэтому был разработан упрощенный алгоритм косинор-анализа для решения этой задачи в условиях, когда только два из трех параметров аппроксимирующей синусоиды остаются неизвестны. Колебательная компонента сезонной динамики Y представлена формулой:
y = R·Cos(t+φ),
где t - время суток, переведенное в радианы, y – значение исследуемого показателя (Ψ), R – амплитуда суточного колебания показателя вокруг нулевого уровня, j – фазовый сдвиг периода колебания показателя относительно точки отсчета.
Параметры кривой определяли по центрированному временному ряду каждого из объектов. Поскольку модель колебаний построена на основе центрированных данных, для определения полной модели необходимо добавить формулу расчета мезора, которая является линейной функцией от переменной времени. Результатом стандартной процедуры линейной одномерной регрессии было выражение вида: x0(d) = a·d + b, где а и b – параметры линейной регрессии, определяемые заданным набором данных; d – независимая переменная (натуральное число), определяющая день, для которого рассчитывается среднесуточное значение; x0 – среднесуточное значение показателя водного режима в конкретный день. Первый день сезона измерений обозначили как d = 1, далее дни пронумеровали последовательно до конца сезона измерений.
С учетом поправки значение показателя водного статуса растения Ψij =Ψ(di,tj) можно рассчитать по формуле:
Ψ(d,t) = a·d + R·Cos(t+φ) + b
Таким образом, на основе статистического исследования трендов сезонной динамики Y березы повислой и карельской березы нами была выбрана аддитивная модель, состоящая из двух частей: суточного колебания относительно среднесуточного значения Y (мезора) и линейного дрейфа самого среднесуточного значения в течение сезона. Все полученные тренды обрабатывали в соответствии с процедурой косинор-анализа.
Результаты
Результатами расчета параметров колебательной модели суточного биоритма Ψ исследуемых форм берез были два множества значений: акрофаза, рассчитанная относительно начала суток (0 часов, 0 минут), и соответствующая ей суточная амплитуда центрированного тренда Ψ. Результаты расчетов для березы повислой и карельской березы представлены в виде кривых сезонного изменения этих двух параметров (рис. 1), сглаженных по методу скользящего среднего с окном, равным трем соседним значениям.
Проведенный анализ показал, что фазовый сдвиг биоритма Ψ с приближением к осеннему периоду увеличивается как у обычной березы повислой, так и у карельской березы, т.е. суточный минимум значений исследуемого показателя удаляется по времени от начала суток. Амплитуда суточного колебания у обеих форм берез также нарастает с приближением конца вегетационного периода. Однако следует отметить, что даже на сглаженном тренде у березы повислой рост амплитуды нарушается краткосрочными провалами, тогда как у карельской березы эти эффекты отсутствуют. Этот факт позволяет предположить большую реактивность Y березы повислой на изменения окружающей среды.
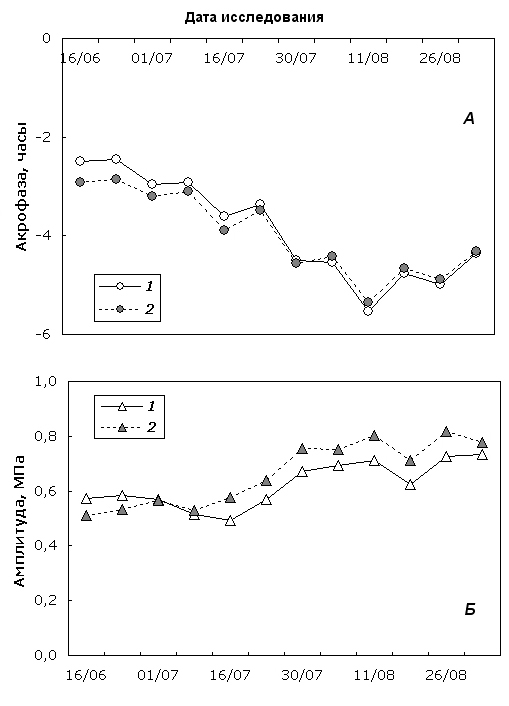
Рис. 1. Сезонная динамика акрофазы (А) и амплитуды (Б) суточного биоритма Ψ березы повислой (1) и карельской березы (2).
Fig. 1. Seasonal dynamics of acrophase (А) and amlitude (Б) of Ψ diurnal rhythm in silver birch (1) and curly birch (2).
Сравнение модельных и исходных значений Ψ показало достаточную точность для обеих форм берез суточной колебательной компоненты модели динамики исследуемого показателя (рис. 2), рассчитанной по данным центрированного тренда для нескольких дней, выбранных из периода наблюдений (16 июня, 24 июня и 1 июля).
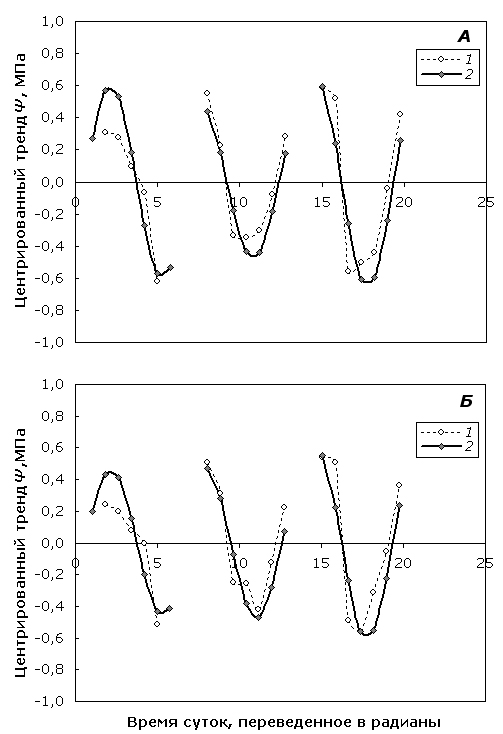
Рис. 2. Соответствие эмпирических (1) и модельных (2) значений колебательной компоненты суточной динамики центрированного тренда Ψ березы повислой (А) и карельской березы (Б).
Fig. 2. Comparison of empirical (1) and modeled (2) values of diurnal dynamics oscillation component of centered Ψ trend in silver birch (А) and curly birch (Б).
Вторая компонента аддитивной математической модели отражает усредненную реакцию водного статуса дерева на изменения окружающей среды и другие внешние воздействия. Проведенный однофакторный дисперсионный анализ ANOVA показал, что среднесуточные значения Ψ, полученные в различные дни в течение всего периода наблюдений, значимо различаются (p<0.05), как у березы повислой, так и у карельской березы. Параметры модели были рассчитаны методом одномерной линейной регрессии (рис. 3).
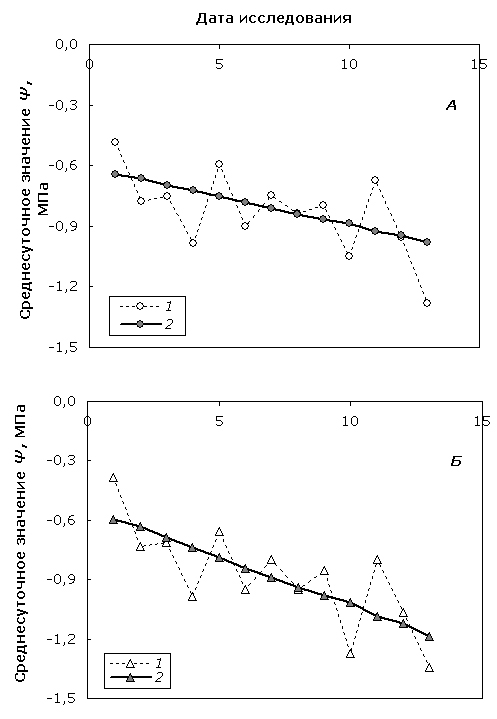
Рис. 3. Сезонная динамика эмпирических (1) и модельных (2) среднесуточных значений Ψ березы повислой (А) и карельской березы (Б).
Fig. 3. Seasonal dynamics of empirical (1) and modeled (2) diurnally mean Ψ values of silver birch (А) and curly birch (Б).
Следует отметить явную тенденцию снижения среднесуточного Ψ по мере приближения к осеннему периоду для обеих форм берез. Колебания значений Ψ вокруг регрессионной прямой показывают, что динамика среднесуточного значения исследуемого показателя также распадается на 2 компоненты. Этот факт позволяет предположить, что система регуляции включает как инерционную составляющую, ответственную за формирование медленной реакции на усредненные внешние воздействия и изменения гомеостаза, так и лабильную часть, оперативно реагирующую на локальные и/или сильные изменения внешних факторов, что требует быстрой настройки системы на оптимальное функционирование или сохранения ее состояния в допустимых для жизнедеятельности пределах. Эти более тонкие взаимосвязи требуют отдельного исследования.
В дальнейшем, сложив две рассчитанные компоненты (суточную колебательную и сезонную линейную), можно получить полную аддитивную математическую модель динамики Ψ деревьев березы в течение вегетационного периода. Так, на рисунке 4 представлена сравнительная динамика реального и расчетного тренда Ψ обеих форм берез, полученная для 5 дней, выбранных из всего пула наблюдений (11, 16, 24 июня и 1, 8 июля).
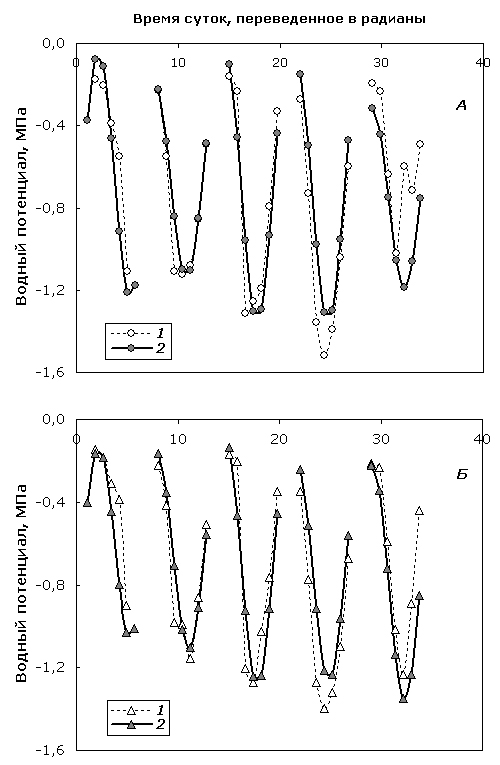
Рис. 4. Сезонная динамика эмпирических (1) и модельных (2) значений Ψ березы повислой (А) и карельской березы (Б) и ее приближение с помощью полной аддитивной модели.
Fig. 4. Seasonal dynamics of empirical (1) and modeled (2) Ψ values of silver birch (А) and curly birch (Б) and its approximation with complete additive model.
Следует отметить, что в результате моделирования сезонной и суточной динамики Ψ исследуемых форм берез были выявлены внутривидовые различия в некоторых параметрах моделей. Так, модельное представление сезонной динамики среднесуточного значения Ψ (рис. 5) облиственных побегов обычной березы повислой и карельской березы значимо различалось (p = 0.005).
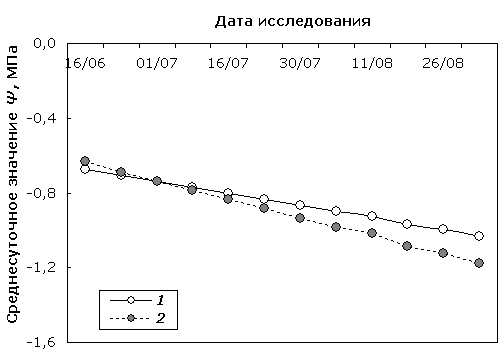
Рис. 5. Линейные компоненты модели сезонной динамики среднесуточных значений Ψ березы повислой (1) и карельской березы (2).
Fig. 5. Linear components of seasonal dynamics model of diurnally mean Ψ values in silver birch (1) and curly birch (2).
Аналогичная закономерность была установлена и в отношении моделирования сезонной динамики амплитуды суточного ритма Ψ (рис. 6), в случае которого исследуемый показатель также значимо различался (р<0.0001) у прямослойной и узорчатой формы березы. Однако следует отметить, что аппроксимация сезонной динамики акрофазы не показала значимых различий (р>0.05) между математическими моделями динамики Ψ для березы повислой и карельской березы. Этот факт, вероятно, свидетельствует о том, что фазовый сдвиг экстремального суточного значения Ψ у деревьев обеих форм берез нарастает одинаково с приближением осеннего периода. При этом более существенные изменения в ходе вегетационного сезона происходят с исследуемым показателем водообмена карельской березы по сравнению с обычной березой повислой.
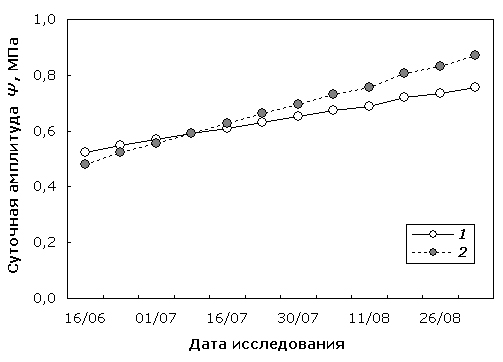
Рис. 6. Линейные компоненты модели сезонной динамики амплитуды суточного ритма Ψ березы повислой (1) и карельской березы (2).
Fig. 6. Linear components of seasonal dynamics model of amplitude of Ψ diurnal rhythm in silver birch (1) and curly birch (2).
Обсуждение
Наиболее вероятной причиной различий в значениях Ψ у разных форм березы повислой является более высокое ксилемное сопротивление у растений карельской березы вследствие аномальной структуры проводящих тканей. Так, например, различия суточных ритмов значений Ψ, вероятно, обусловлены тем, что днем запасы влаги в водопроводящей системе минимальны, а сопротивление ее движению максимально (Сазонова и др., 2011). Кроме того, факт устойчивой тенденции более низких величин Ψ у побегов карельской березы в вегетационной динамике, вероятно, обусловлен разницей в величине осмотической составляющей общего водного потенциала исследуемых форм березы. Известно, что вклад осмотического потенциала в общий водный потенциал у древесных растений незначителен, поскольку концентрация растворенных веществ в ксилемном соке мала (Kozlowski et al. 1991; Marschner, 1996). Однако у карельской березы в период активных ростовых процессов происходит увеличение концентрации ксилемного сока вследствие интенсивного оттока ассимилятов в стволовую часть (камбиальную зону), в которой на фоне высокой водопроводимости ксилемы во флоэме происходит накопление избыточного количества транспортной сахарозы, что, в свою очередь, индуцирует аномальный камбиальный рост (Новицкая, 2008). Кроме того, ранее нами (Сазонова и др., 2012) уже было показано увеличение степени различий водного дефицита и насыщающего содержания воды в листе березы повислой и карельской березы с усилением выраженности узорчатой текстуры древесины ствола в онтогенезе. При этом структурной основой поддержания высокой оводненности тканей листа карельской березы и водного баланса на постоянном уровне при изменении условий среды может служить наличие резервного пула воды в вакуолях паренхимных клеток древесины и коры (Новицкая, 2011), что, в свою очередь, вероятно, нивелирует влияние внутривидовых структурных отличий и обуславливает однонаправленность изменений суточных ритмов водного потенциала облиственных побегов березы повислой и карельской березы в вегетационной динамике. Очевидно, что адаптационная стратегия древесного растения направлена на поддержание оводненности его тканей и органов на довольно стабильном уровне, необходимом для успешного функционирования важнейших метаболических путей и синтеза органических соединений.
Заключение
Проведенное исследование подтвердило предположение о взаимосвязи между структурной организацией проводящих тканей ствола древесного растения и переменными водообмена. Сравнительный анализ суточных ритмов водного потенциала побегов березы повислой и карельской березы выявил однонаправленность изменений исследуемого показателя в вегетационной динамике при разной его вариабельности. Более существенные изменения в ходе вегетационного сезона происходят с водным потенциалом облиственных побегов у карельской березы по сравнению с обычной березой повислой. Выполненное моделирование биоритмов физиологических показателей позволило провести более детальный анализ временных рядов значений показателя водного статуса растения и выявить специфические внутривидовые различия, которые сложно обнаружить при обычной статистической обработке экспериментальных данных.
Библиография
Ашофф Ю. Биологические ритмы / Пер. с англ. М.: Мир, 1982. 414 с.
Багриновский А. К., Багинская Н. В., Баженова А. Ф., Колпаков М. Г., Маркель А.П. Математический анализ циркадных систем организма на основании процедуры «Косинор» // Кибернетические подходы к биологии. Новосибирск, 1973. C. 196−209.
Ветчинникова Л. В. Береза: вопросы изменчивости (морфофизиологические и биохимические аспекты) . М.: Наука, 2004. 183 с.
Гланц С. Медико-биологическая статистика / Пер. с англ. М.: Практика, 1999. 459 с.
Емельянов И. П. Формы колебаний в биоритмологии . Новосибирск: Наука, 1976. 128 с.
Ермаков В. И. Механизмы адаптации березы к условиям Севера . Л.: Наука, 1986. 144 с.
Карп В. П. Математические методы исследования биоритмов // Хронобиология и хрономедицина / Ред. О. М. Комаров. М.: Медицина, 1989. С. 29−45.
Новицкая Л. Л. Карельская береза: механизмы роста и развития структурных аномалий . Петрозаводск: Verso, 2008. 144 с.
Новицкая Л. Л. Механизмы индукции аномального камбиального роста древесных растений на примере карельской березы // Матер. междун. конф. «Структурные и функциональные отклонения от нормального роста и развития растений под воздействием факторов среды». Петрозаводск, 2011. С. 225-230.
Сазонова Т. А., Болондинский В. К., Придача В. Б. Эколого-физиологическая характеристика сосны обыкновенной . Петрозаводск: Verso, 2011. 207 с.
Сазонова Т. А., Позднякова С. В., Придача В. Б. Особенности водного режима Betula pendula (BETULACEAE) с нормальной и аномальной древесиной ствола в онтогенезе // Бот. журн. 2012. № 11. С. 1435−1447.
Сенькина С. Н. Водный режим сосны и ели в фитоценозах Севера . Екатеринбург: РИО УрО РАН, 2013. 104 с.
Хальберг Ф. Хронобиология // Кибернетический сборник. 1972. № 9. C. 189−247.
Шереметьев С. Н. Травы на градиенте влажности почвы (водный обмен и структурно-функциональная организация) . М: Т-во науч. изд. КМК, 2005. 271 с.
Brodersen C. R., McElrone A. J. Maintenance of xylem network transport capacity: a review of embolism repair in vascular plants // Front Plant Sci. 2013. Vol. 4. P. 108−119. doi:10.3389/fpls.2013.00108.
Bucci S. J., Scholz F. G., Campanello P. I., Montti L., Jimenez-Castillo M., Rockwell F. A. Hydraulic differences along the water transport system of South American Nothofagus species: do leaves protect the stem functionality? // Tree Physiol. 2012. Vol. 32. P 880–893. doi:10.1093.
Glantz S. A., Slinker B.K. Primer of applied regression and analysis of variance. N.Y.: McGraw-Hill, 2003. P. 162−318.
Kaipiainen L., Nirinmaa E., Marine M., Sazonova T. Geographical variation in the regularities of woody structure and water transport // Acta forestalia fennica. Production Process of Scots Pine: Geographical Variation and Models. Helsinki, 1996. Vol. 254. P. 49–78.
Kozlowski T., Kramer P., Pallardy S. The physiological ecology of woody plants. London: Academic press, 1991. 657 p.
Marschner H. Mineral nutrition of higher plants. London: Academic press, 1996. 889 p.
Scoffoni C., Vuong C., Diep S., Cochard H., Sack L. Leaf shrinkage with dehydration: coordination with hydraulic vulnerability and drought tolerance // Plant Physiology. 2014. Vol. 164. Р. 1772–1788.
Sellin A. Hydraulic and stomatal adjustment of Norway spruce trees to environmental stress // Tree Physiol. 2001. Vol. 21. P. 879–888.
Благодарности
Работа выполнена в рамках государственного задания ИЛ КарНЦ РАН и при частичной финансовой поддержке РФФИ (гранты 09-04-00299-а и 13-04-00827-а).






 © 2011 - 2026
© 2011 - 2026