Введение
Масштабные биогеографические и экосистемные исследования, проводимые в рамках международных программ, обусловили поиск путей адекватной количественной оценки биологического разнообразия, что одновременно является средством осмысления сущности этого непростого явления (Hurlbert, 1971; Magurran, 2004; Ricotta, Szeidl, 2006). Являясь типичным искусственно сконструированным понятием, разнообразие, однако, позиционируется как комплексный критерий, отражающий одновременно три важнейших характеристики сообществ:
1) богатство, или общее число элементов S: видов, таксонов, функциональных групп, характерных признаков, узловых точек эволюции и т. д.;
2) выравненность, или степень неравномерности статистического распределения относительных частот pi встречаемости отдельных компонент;
3) экологические расстояния, или меру различий dij между отдельными элементами внутри сообщества. Под последними могут пониматься: таксономическая удаленность (число узлов, разделяющих виды i и j на дереве линнеевской классификации), генетическая дивергенция (результат сравнения участков последовательностей ДНК, принадлежащие двум генотипам), функциональные отличия в пространстве характеристических признаков и др.
Важнейшей проблемой поиска оценки «истинного» разнообразия (true diversity) является соизмерение относительной количественной значимости перечисленных характеристик в процессе их обобщения. Особое значение это имеет при сравнении биоразнообразия двух или нескольких местообитаний, когда необходимо найти разумный баланс между вкладами редких и фоновых видов.
Цель настоящей работы – на примере донных сообществ средней равнинной реки проанализировать современные методики сравнительной оценки уровня видового и таксономического разнообразия экосистем, включая проверку статистических гипотез об их однородности.
Материалы
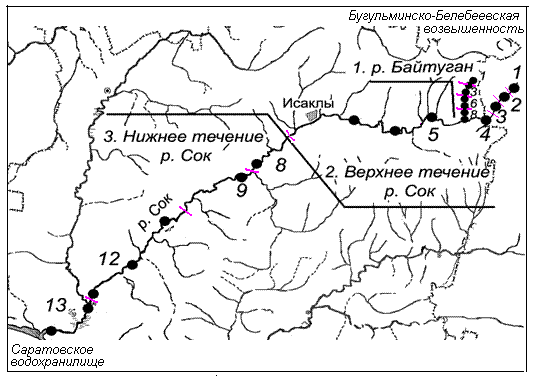
Анализ оценок разнообразия проводился по данным гидробиологической съемки, выполняемой в течение ряда лет на всем протяжении р. Сок (длина 375 км), которая является незарегулированной равнинной рекой II–IV класса качества вод, и ее притока р. Байтуган предгорного типа (22 км). Всего по результатам 147 проб было обнаружено 374 таксономические группы донных организмов, определенные, как правило, с точностью до вида (Особенности пресноводных, 2011). С учетом гидрологических характеристик по продольному профилю рек выделено 13 биотопически однородных участков (см. рис. 1), на каждом из которых было выполнено примерно одинаковое количество гидробиологических проб (от 9 до 11). Для проведения расчетов были сформированы матрицы N и P размерностью 13x374, которые включали суммарные значения численности Ni особей каждого i-го вида и их относительные доли pi от общей численности бентосных организмов во всех пробах, взятых на каждом из 13 участков.
Рис. 1. Схема расположения участков и станций гидробиологической съемки на реке Сок
Fig. 1. The scheme of sites and stations of hydrobiological sampling on the river Sok
Вся обработка данных была выполнена с использованием свободно распространяемых программных модулей статистической среды R (R Development, 2012).
Традиционные методы исследований
Предполагается, что большое изменение видового разнообразия экосистемы должно вызвать адекватное изменение значения оценивающего его показателя. В имеющейся практике видовое разнообразие оценивается с использованием императивных индексов, основанных на предположении о «нейтральности» видов (т. е. при равном экологическом расстоянии между ними, dij = const). Например, среднее логарифмическое из S частот pi называют информационным индексом Шеннона H (Shannon, Weaver, 1949; Розенберг, 2009) и он соответствует среднему минимальному числу испытаний, в результате которых из сообщества будет извлечена особь самого многочисленного вида. Другая популярная мера видового разнообразия – индекс Джини–Симпсона – равен смещенной оценке дисперсии частот pi. Таким образом, эти меры дают только косвенную оценку биоразнообразия, подобно тому как радиус является косвенной оценкой площади круга.
Пусть (Jost, 2006) на континенте присутствует миллион видов с одинаковой численностью и произвольное катастрофическое воздействие (например, падение метеорита) убивает 999 900 видов, оставляя только 100 из них. Любой эколог сказал бы в этом случае, что воздействие метеорита вызвало огромное абсолютное и относительное понижение разнообразия. Однако популярный индекс Симпсона–Джини уменьшается при этом только от 0,999999 до 0,99 (снижение менее чем на 1 %). Очевидно, что поведение этой меры не соответствует интуитивному понятию разнообразия, и биологи, полагающиеся на индекс Симпсона, могут недооценивать величину изменений в экосистеме. В этих же условиях индекс Шеннона уменьшается с 19,9 до 6,6, т. е. уменьшение видового богатства в 10 000 раз сопровождается снижением меры разнообразия только в 3 раза. Это не означает, что шенноновская энтропия – неудачная мера, но её значение оценивает неопределенность, а не разнообразие.
Другим спорным моментом оценки разнообразия является иерархическая организация биологических сообществ. В наиболее общем смысле под биологическим разнообразием подразумевают «разнообразие жизни». Это понятие охватывает как филогенетическое разнообразие различных видов, так и более высоких таксономических единиц (семейств, классов, типов и т. д.), а также разнообразие сред обитания и экосистем.
Оригинальные методы исследований
1. «Эффективное видовое богатство» и числа Хилла
Обобщением энтропии Шеннона, учитывающим возможную нелинейность логарифмических функций от pi для отдельных элементарных компонент, является семейство обобщенных энтропий Реньи qH порядка q – см. табл. 1. При увеличении q возрастает вклад, который вносят в показатель энтропии виды с высокой представленностью (доминанты). Верно также обратное утверждение: при снижении q растет вклад редких видов, особенно при уходе в область отрицательных значений.
Таблица 1. Связь индексов энтропии–разнообразия с показателями «истинного разнообразия» Хилла–Джоста; приведены значения γ-разнообразия для разделов р. Сок
Table 1. Relation of indices of entropy–diversity with Hill–Jost’s measures «true» diversity; values γ-diversity for sections the river Sok are presented.
Индексы видового разнообразия, основанные на энтропии или дисперсии, обладают рядом привлекательных свойств (Ricotta, 2003): (1) симметричность относительно своих аргументов; (2) расширяемость, т. е. добавление видов с нулевым обилием не изменяет оценки полного разнообразия; (3) «монотонность», т. е. перемещение единицы обилия от массового к более редкому виду не уменьшает разнообразия; (4) однородность, т. е. разнообразие зависит только от относительных частот видов, а не от их абсолютного обилия. Однако для них не соблюдается два других ключевых правила: удвоения (Hill, 1973) и нормализации (Jost, 2006).
Принцип удвоения (или репликации) утверждает, что если объединить два сообщества с непересекающимися списками видов, у которых одинаковые функции распределения обилия p и богатство S, то первоначальная оценка разнообразия должна быть удвоена. Нормализация разнообразия сводится к задаче поиска эквивалентного сообщества, составленного из видов с одинаковой встречаемостью pi, у которого значение показателя разнообразия численно то же самое, что и у реально рассматриваемого сообщества. То есть если в сообществе присутствует S видов с одинаковым обилием, то мера его разнообразия должна быть максимальна и равна S. В противном случае, при гетерогенности частот pi, количество видов Sэкв эквивалентного сообщества, S > Sэкв, будет отражать «эффективное богатство видов» (MacArthur, 1965) или состоятельную оценку разнообразия изучаемого сообщества.
Обоим этим правилам удовлетворяет экспоненциальная форма энтропий Реньи, называемая числами Хилла (см. табл. 1), которые можно трактовать как обобщенные показатели разнообразия qD порядка q, зависящие только от значения q и частот обилия видов p. Ряд исследователей (Jost, 2006, Tuomisto, 2010; De'ath, 2012) видят в числах Хилла концептуально особый смысл и интуитивно приписывает им свойства «истинного» (или подлинного) разнообразия, отличая тем самым от десятка других энтропийных индексов или показателей иной функциональной формы.
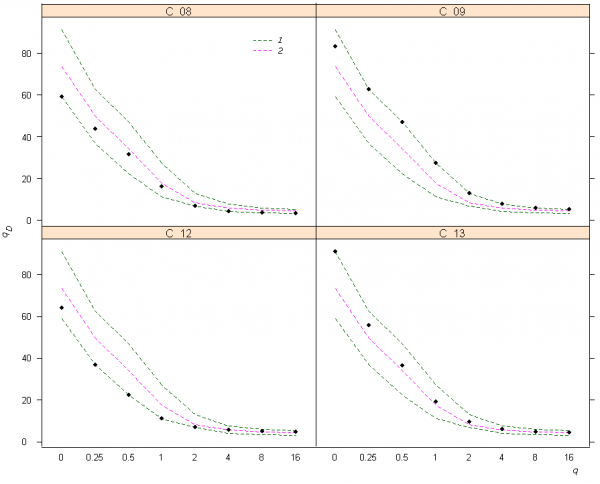
Содержательный анализ изменчивости разнообразия с использованием чисел Хилла сводится к графической интерпретации кривых зависимости qD от порядка q. Например, на рис. 2 можно усмотреть, что максимум богатства видов в нижнем разделе р. Сок приходится на устьевой участок С_13, однако при увеличении q приоритет в уровне разнообразия переходит к участку С_09, где не столь выражено доминирование олигохет и эврибионтных таксонов хирономид.
Рис. 2. Кривые зависимости показателей qD видового разнообразия Хилла–Джоста от порядка q для четырех участков в нижнем течении р. Сок: 1 – минимальная и максимальная огибающие кривые, 2 – медиана; использована функция renyi(…) пакета vegan статистической среды R
Fig. 2. Curves of «true» diversity indices qD of Hill-Jost depending on the order q for four sites in the bottom sections of the river Sok: 1 – the minimum and maximum envelopes, 2 – a median; function renyi(…) of vegan package in statistical environment R is used
2. Сравнительный анализ групп местообитаний
Если рассматривать видовое γ-разнообразие для группы из n участков, то общий энтропийный индекс Шеннона Hγ в силу своей аддитивности рассчитывается с использованием частот обилия 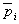 , средних для всех участков. Аналогично α-разнообразие в первом приближении может быть рассчитано как среднее разнообразие по совокупности проб внутри каждого однородного участка:
, средних для всех участков. Аналогично α-разнообразие в первом приближении может быть рассчитано как среднее разнообразие по совокупности проб внутри каждого однородного участка: 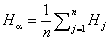 (De'ath, 2012). Тогда β-разнообразие (или дифференцирующее разнообразие между отдельными участками) будет равно Hβ = Hγ – Hα.
(De'ath, 2012). Тогда β-разнообразие (или дифференцирующее разнообразие между отдельными участками) будет равно Hβ = Hγ – Hα.
Нетрудно заметить, что с учетом соотношения 1D= eH разложение разнообразия на компоненты для чисел Хилла при q = 1 будет 1Dβ= 1Dγ / 1Dα, т. е. β-разнообразие приобретает смысл относительного прироста эффективного числа видов при объединении участков. Подробное рассмотрение всех аспектов «новой» концепции оценки α-, γ- и β-разнообразия и способов пропорционирования частот pi представлено в работах (Jost, 2007; Tuomisto, 2010a, b).
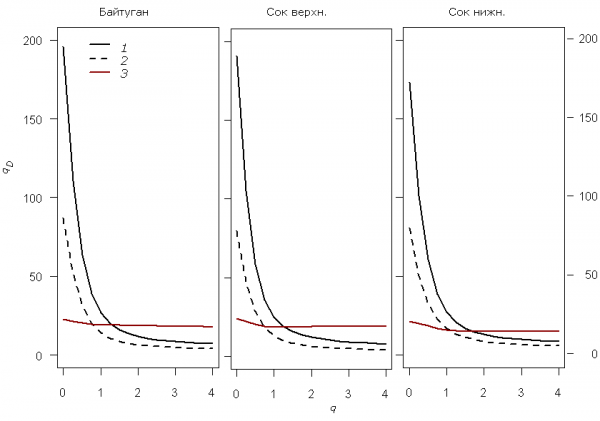
Значения γ-разнообразия для трех групп участков, объединяющих верхний и нижний разделы р. Сок и р. Байтуган, приведены в табл. 1, а на рис. 3 представлены кривые зависимости трех компонентов разнообразия α, γ и β от порядка чисел Хилла q. Не обращая внимание на немногие частные отличия, отметим, что значения показателей «истинного» видового разнообразия для анализируемых трех зон на всех уровнях разложения оказались весьма близкими: например, β-разнообразие варьирует в интервалах от 2.14 до 2.4 (q = 0) и от 1.5 до 1.89 (q = 2). Однако поставим своей целью подтвердить предположение об однородности видового разнообразия в группах участков статистическими методами.
Рис. 3. Разложение показателей видового разнообразия Хилла–Джоста на компоненты в зависимости от порядка q для трех разделов р. Сок; использована функция trudi(…) пакета simba R: 1 – γ-разнообразие, 2 – α-разнообразие, 3 – β-разнообразие
Fig. 3. Partitioning of Hill–Jost’s «true» diversity indices into α- γ- and β-components depending on the order q for three sections of the river Sok; function trudi(…) of simba package R is used: 1 – γ-diversity, 2 – α-diversity, 3 – β-diversity
Оценка различий показателей видового разнообразия для трех или более сообществ основана на алгоритмах множественных парных сравнений в рамках моделей однофакторного дисперсионного анализа (ANOVA). При этом сравнивается не только γ-разнообразие групп, но и учитывается внутригрупповая дисперсия α-разнообразия для отдельных участков. Пусть мы имеем матрицу частот P из S строк (виды) и столбцов наблюдений (пробы или средние численности по участкам), каждый из которых относится к k-й группе, j = 1, …, Jk, k = 1, …, L. При таком способе группировки по обычным формулам ANOVA можно вычислить:
° значения индекса видового разнообразия Ijk для каждого j-го участка (т. е. столбца);
° групповые средние 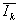 для каждой k-й группы участков из L;
для каждой k-й группы участков из L;
° остатки εjk = Ijk – 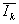 , групповые средние остатков
, групповые средние остатков 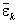 и оценку остаточной дисперсии
и оценку остаточной дисперсии 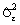 .
.
Между выделяемыми группами возможно M множественных сравнений, механизм реализации которых определяется матрицей С априорных ортогональных контрастов. Коэффициенты контрастов cmi задают смысл проверяемых гипотез и подчиняются условию 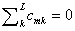 для всех m = 1, …, M. Например, матрица контрастов Тьюки СТ определяет при L = 3 все возможные переборы трех групп, а контрасты Даннета СD – механизм сравнения контрольной группы со двумя остальными.
для всех m = 1, …, M. Например, матрица контрастов Тьюки СТ определяет при L = 3 все возможные переборы трех групп, а контрасты Даннета СD – механизм сравнения контрольной группы со двумя остальными.
Метод бутстреп-оценки одновременных (simultaneous) доверительных интервалов тестовой статистики при сравнении произвольного индекса I в нескольких группах описан в работах Р. Шерера с соавторами (Scherer, Schaarschmidt, 2013). Набор M из p-значений, скорректированных с учетом множественных сравнений между группами (multiplicity-adjusted p-values), рассчитывается следующим образом:
1. Выполняется непараметрический бутстреп вектора остатков εjk. Случайный выбор с возвращениями осуществляется только в пределах каждой группы из L. Вычисляются групповые средние 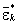 и общая дисперсия остатков
и общая дисперсия остатков 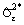 на бутстреп-выборке.
на бутстреп-выборке.
2. Для каждого m-го варианта парного сравнения групп вычисляется статистика межгрупповых отличий 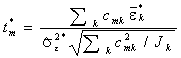 , учитывающая контрасты k-й группы.
, учитывающая контрасты k-й группы.
3. Шаги 1–2 повторяются B раз и на каждой b-й итерации находится максимум 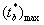 из всех возможных m-х вариантов парного сравнения.
из всех возможных m-х вариантов парного сравнения.
4. Пусть Rbm = 0 при tm > и Rbm = 1 в противном случае, где tm – эмпирическое значение тестовой статистики. Тогда скорректированное p-значение для m-го контраста с учетом множественных сравнений будет равно 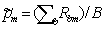 .
.
В табл. 2 представлены результаты сравнения видового разнообразия по индексу Шеннона донных сообществ для трех зон системы водотоков Сок–Байтуган, объединяющих 13 участков этих рек. При использовании контрастов Даннета в качестве контрольного региона была взята р. Байтуган. Нулевая гипотеза об однородности уровня видового разнообразия на всем протяжении речной системы не отклоняется.
Таблица 2. Сравнение видового разнообразия трех разделов р. Сок с использованием функции sbdiv(…) пакета simboot R; обрабатывалась матрица 13x374 средних численностей видов на 13 участках; tm – эмпирическая статистика (аналог t Стьюдента); CIl и CIu – нижний и верхний доверительные интервалы; p и padj – уровни значимости без учета и с учетом множественных сравнений
Table 2. Comparison of a species diversity of three sections of the river Sok with function sbdiv(…) a package simboot R use; the matrix 13x374 average abundance of species on 13 sites was processed; tm – the empirical statistics (analogue t Student); CIl and CIu – the bottom and top confidential intervals; p and padj – significance values without taking into account and taking into account multiple comparisons
| Сравниваемые участки | tm | CIl | CIu | p | padj |
| 1. Использование контрастов Тьюки (все возможные переборы) | |||||
| Сок_верх – Байтуган | –0.063 | –0.896 | 0.769 | 0.828 | 0.976 |
| Сок_нижн – Байтуган | 0.150 | –0.727 | 1.028 | 0.651 | 0.876 |
| Сок_нижн – Сок_верх | 0.214 | –0.619 | 1.046 | 0.486 | 0.744 |
| 2. Использование контрастов Даннета (контрольная группа – «Байтуган») | |||||
| Сок_верх – Байтуган | 0.063 | –0.876 | 0.749 | 0.853 | 0.968 |
| Сок_нижн – Байтуган | 0.150 | –0.706 | 1.007 | 0.636 | 0.852 |
Аналогичные выводы были получены также на основе расчетов, выполненных при сравнении чисел Хилла в диапазоне q от –1 до 3 с использованием функции mcpHill(…) пакета simboot (Pallmann et al., 2012).
3. Таксономическое разнообразие, основанное на числах Хилла
«Филогенетическое разнообразие является более обоснованным индикатором сохранения биологических ресурсов, чем богатство видов, а оценка его с использованием длины ветвей (таксономического дерева) выглядит лучшей из возможных процедур, основанной лишь на топологии» (Crozier 1997, p. 243). Ранее нами (Шитиков, Зинченко, 2013) на примере данных гидробиологической съемки донных сообществ реки Сок рассматривались индексы таксономического разнообразия, использующие квадратичную энтропию Рао Q =  , где di – длина пути, который связывает виды i и j на дереве линнеевской классификации.
, где di – длина пути, который связывает виды i и j на дереве линнеевской классификации.
Другой подход, основанный на формуле информационной энтропии Шеннона, представлен индексом таксономической энтропии (Ricotta, Avena, 2003):
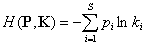 ;
; 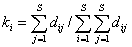 ;
; 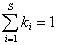 ,
,
где P – вектор относительного обилия множества видов S в сообществе; K = (k1, k2, …, ks) - вектор относительных вкладов видов в таксономическое разнообразие, который вычисляется путем взвешенного усреднения значений dij в строках матрицы расстояний D, учитывающей филогенетические различия между видами.
Таксономическая энтропия Риккоты – Авены может быть разложена на две неотрицательные составляющие – традиционную энтропию Шеннона H(P) и дивергенцию Кульбака H(P||K), учитывающую прирост информации в экосистеме за счет разнообразия таксонов рангом выше вида:
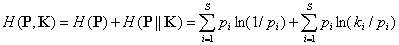 .
.
Б. Аллен с соавторами (Allen et al., 2009), изучив на сообществах летучих мышей статистические свойства таксономических энтропий, показали, что H(P, K) и H(P||K) иногда могут монотонно уменьшаться с увеличением видового богатства, что противоречит основным принципам оценки биоразнообразия. Они предложили новую модификацию индекса разнообразия Шеннона – индекс филогенетической энтропии:
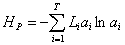 ,
,
где Li – длина i-й ветви иерархического филогенетического дерева T для сообщества, ai – относительное суммарное обилие видов, которые представлены «листьями», связанными с ветвью i.
Энтропийные индексы H(P, K) и Hp не удовлетворяют принципам репликации (удвоения), поэтому было предложено (Chao et al., 2010) распространить подход Хилла–Джоста на оценку «истинного» разнообразия для таксономического дерева с L уровнями классификации. Тогда можно записать обобщенное выражение для среднего филогенетического разнообразия порядка q: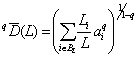 , где BL – множество всех ветвей в интервале уровней иерархии [0, L], Li – длина i-й ветви в множестве BL, а ai является полным обилием видов, связанных с этой ветвью. Тогда общая мера разнообразия qD(L) =
, где BL – множество всех ветвей в интервале уровней иерархии [0, L], Li – длина i-й ветви в множестве BL, а ai является полным обилием видов, связанных с этой ветвью. Тогда общая мера разнообразия qD(L) = 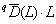 определяет эффективное (т. е. эквивалентное заданному порядку q) количество классификационных узлов филогенетического дерева. Она численно равна разнообразию сообщества, состоящего из z видов с равным числом особей, причем каждый вид принадлежит к своему уникальному роду, семейству и т. д. (т. е. имеется z ветвей, исходящих от корня).
определяет эффективное (т. е. эквивалентное заданному порядку q) количество классификационных узлов филогенетического дерева. Она численно равна разнообразию сообщества, состоящего из z видов с равным числом особей, причем каждый вид принадлежит к своему уникальному роду, семейству и т. д. (т. е. имеется z ветвей, исходящих от корня).
Легко показать, что таксономическое обобщение чисел Хилла, выполненное А. Чао с соавторами, в частных случаях q с точностью до элементарных преобразований сводится к описанным выше мерам:
° при q = 0 – к кладистическому разнообразию 0D(L) = CD (Vane-Wright et al., 1991), т. е. общему числу узлов дерева;
° при q = 1 – к индексу филогенетической энтропии Аллена, 1D(L) = exp(Hp);
° при q = 2 – к квадратичной энтропии Рао, 2D(L) = 1/(1 – Q).
Для оценки показателей таксономического разнообразия были выполнены следующие действия:
° формировалась общая таксономическая таблица размерностью 11x374, состоящая из наименований 11 систематических уровней для каждого из 374 видов донных организмов в реках Сок–Байтуган согласно линеевской классификации: вид → род → триба → подсемейство → семейство → подотряд → отряд → подкласс → класс → подтип → тип;
° рассчитывалось таксономическое расстояние между каждой парой видов и с использованием функции taxa2dist(…) пакета vegan формировалась квадратная симметричная матрица D размерностью 374x374;
° вычислялся вектор K вкладов всех S видов макрозообентоса, и для каждого участка или их группы находились индексы таксономической энтропии (Ricotta, Avena, 2003);
° с использованием метода средней связи формировалось таксономическое дерево видов (рис. 4), которое было сохранено в формате Newick и преобразовано в ультраметрическое филогенетическое дерево (функции пакета ape);
° для расчета показателей таксономического разнообразия на основе чисел Хилла использовался комплект скриптов R в составе компьютерной программы PhD (Phylogenetic Diversity – Chao et al., 2010), дополненный нами процедурой проверки статистической гипотезы методом рандомизации.
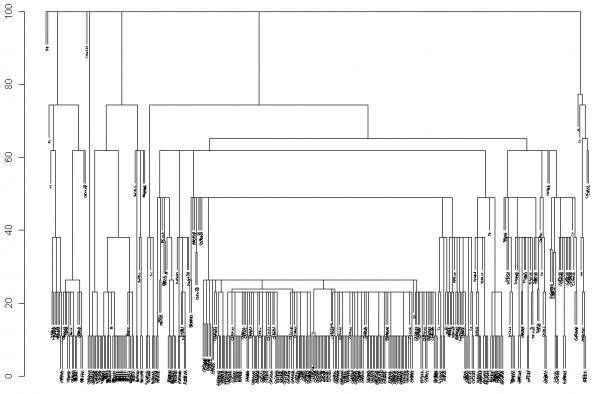
Рис. 4. Таксономическое дерево линеевской классификации 374 видов макрозообентоса, обнаруженных в пробах на р. Сок; использована функция hclust(…) пакета stats R
Fig. 4. The taxonomic tree of Linnaean systematics of 374 species of macrozoobenthos, found in the river Sok; function hclust(…) of stats package R is used
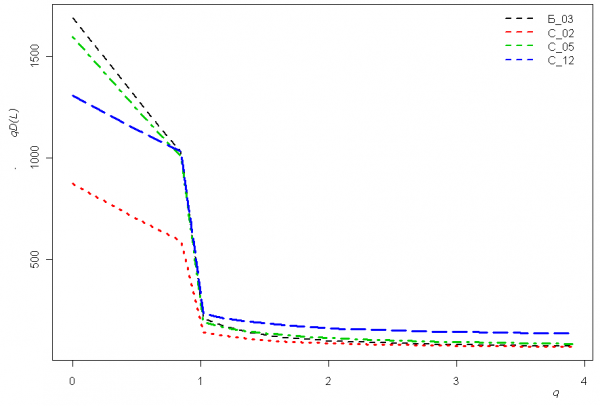
Профили зависимости общего таксономического разнообразия qD(L) от порядка q для четырех характерных участков системы водотоков представлены на рис. 5. Нетрудно отметить, что при q = 0 (т. е. без учета численности видов) максимальное разнообразие имеет место в реке Байтуган Б_03 и среднем участке р. Сок С_05, тогда как уже при q = 1 (т. е. основанной на формуле энтропии Шеннона–Аллена) приоритет переходит к устьевому участку С_12.
Рис. 5. Графики зависимости показателей qD(L) таксономического разнообразия от порядка q для четырех различных участков р. Сок, полученные программой PhD, использующей среду R
Fig. 5. Curves of «true» taxonomic diversity indices qD depending on the order q for 4 diffferent segments of the river Sok, received by PhD program using environment R
Поставим задачу оценить статистическую значимость парных отличий таксономического γ-разнообразия донных сообществ группы участков в нижнем течении р. Сок от двух остальных разделов водотоков – табл. 3. Нулевая гипотеза о равенстве произвольного показателя разнообразия I для двух сравниваемых групп может быть проверена с использованием рандомизационного теста, состоящего из следующих шагов (Шитиков, Розенберг, 2013):
1. Рассчитывается разность эмпирических показателей Δobs = I1 – I2, полученных для сравниваемых групп 1 и 2 с использованием наблюдаемых частот обилия видов pi.
2. Для случайного набора видов Sper из S, Sper ≈ 0.5S, значения частот меняются местами, т. е. pi1 → pi2 и pi2 → pi1, и рассчитывается разность Δsim показателей разнообразия, полученных из предположения, что видовой состав обеих групп является однородным и статистически случайным.
3. Шаг 2 повторяется многократно В раз и рассчитывается В значений Δsim при справедливости нулевой гипотезы (поскольку имитируемые показатели основаны на случайных наборах частот). Статистическое распределение Δsim дает возможность найти среднюю разность mD (как правило, близкую к нулю) и ее доверительные интервалы: если значение Δobs находится за доверительными пределами, то нулевая гипотеза об однородности разнообразия отклоняется.
3. Статистическая значимость нулевой гипотезы, может быть оценена по формуле р = (b + 1)/(B + 1), где b – число итераций рандомизации, для которых абсолютная величина Δsim превысила Δobs.
Таблица 3. Показатели таксономического (филогенетического) разнообразия трех разделов изучаемой системы водотоков и результаты проверки нулевой гипотезы при парных сравнениях нижнего течения р. Сок с двумя остальными разделами
Table 3. Taxonomic (phylogenetic) diversity measures for three sections of water system under study and results of testind of a null-hypothesis for pairwise comparisons of the bottom sections of the river Sok with two other sections
| Показатели разнообразия | Разделы системы водотоков | Р-значения парных сравнений | |||
| Байтуган | Сок верхн. | Сок нижн. | Сок_нижн – Байтуган | Сок_нижн – Сок_верх | |
| Энтропия Риккоты–Авены H(P, K) | 5.992 | 5.995 | 5.993 | 0.999 | 0.999 |
| Филогенетическое разнообразие
qD(L) , q = 0 |
2818 | 2697 | 2680 | 0.582 | 0.98 |
| q = 1 или exp(Hp) | 222.6 | 245 | 296.7 | 0.094 | 0.199 |
| q = 1.5 | 133.9 | 157.1 | 204.1 | 0.015 | 0.174 |
| q = 2 | 103.6 | 122.6 | 167 | 0.005 | 0.134 |
| q = 2.5 | 89.3 | 105.1 | 146.6 | 0.005 | 0.069 |
| q = 3 | 81 | 94.8 | 133.2 | 0.01 | 0.054 |
Обсуждение
Расчеты показали, что таксономическая энтропия в модификации Рикотты и Авены H(P, K) основывается на недостаточно интерпретируемом «среднем таксономическом расстоянии» ki вида i от всех остальных, т. е. по существу не учитывает межвидовые различия dij как таковые. Кроме того, поскольку вектор K имеет, как правило, существенно меньшую статистическую вариацию, чем P, то после замены в формуле Шеннона ln(pi) на ln(ki) новый показатель сильно теряет чувствительность при оценке выравненности сообществ, мало что приобретая взамен. Напротив этому, для филогенетической энтропии Hp, предложенной Алленом с соавторами, характерно вполне гармоничное соизмерение всех трех составляющих разнообразия: выравненности, богатства видов и межвидовых отличия.
Распространение формулы для чисел Хилла на показатели таксономического разнообразия, выполненное Чао с соавторами, вносит дополнительные возможности в анализ особенностей видовой структуры сообществ. Представленные в табл. 3 профили изменения qD(L) дают возможность установить, что при увеличении порядка q монотонно возрастет превышение таксономического разнообразия в нижней части р. Сок над аналогичными показателями для других разделов водотока. Уже при q = 1.5 такое превышение по сравнению с р. Байтуган становится статистически значимым. С экологических позиций это означает, что подмножество видов-доминантов на устьевых участках водотока принадлежит к разным таксонам (моллюски, олигохеты, пелофильные хирономиды и ракообразные). В противоположность этому, донное сообщество р. Байтуган таксономически более разнообразно в области минорных видов, но доминантную часть видового состава образует весьма компактная группа реофильных хирономид.
Заключение или выводы
Все эти экологические нюансы не могли быть обнаружены при оценке биоразнообразия на основе индексов, использующих концепцию «нейтральных видов». Представленный опыт апробации показателей таксономического разнообразия на примере лотических систем свидетельствует о существенном расширении возможностей комплексного анализа биоценотической структуры с привлечением дополнительной информации о дифференциации видов. Отработка методик расчета и изучения статистических свойств этих показателей является актуальной задачей биоэкологических исследований. Проведенный анализ динамики индексов таксономического и функционального разнообразия для р. Сок в целом подтверждается выводами, полученными при комплексном исследовании экологического статуса водотока (Особенности пресноводных…, 2011). Это позволяет вполне обоснованно рекомендовать их к использованию в прикладных целях или для принятия природоохранных решений.
Файлы с исходными данными и скрипты для их обработки в статистической среде R, полностью воспроизводящие все представленные расчеты, могут быть свободно скачаны читателями с ресурса http://www.ievbras.ru/ecostat/Kiril/Download/Hill_Div.zip (дата обращения: 20.12.2013).
Библиография
Особенности пресноводных экосистем малых рек Волжского бассейна / Под редакцией Розенберга Г.С., Зинченко Т.Д. Тольятти: Кассандра, 2011. 322 с.
Розенберг Г. С. Информационный индекс и разнообразие: Больцман, Котельников, Шеннон, Уивер… // Самарская Лука: проблемы региональной и глобальной экологии. 2010. Т. 19, № 2. С. 4–25.
Шитиков В. К., Зинченко Т. Д. Изменение индексов таксономического разнообразия сообществ макрозообентоса по продольному градиенту рек // Принципы экологии. 2013. № 2. С. 46–56.
Шитиков В. К., Розенберг Г. С. Рандомизация и бутстреп: статистический анализ в биологии и экологии с использованием R. Тольятти: Кассандра, 2013. 314 с. URL: http://www.ievbras.ru/ecostat/Kiril (дата обращения: 20.12.2013).
Chao A., Chiu C.-H., Jost L. Phylogenetic diversity measures based on Hill numbers // Philos. Trans. R. Soc. Lond. Ser. B – Biol Sci. 2010. N 365. Р. 3599–3609.
Crozier R.H. Preserving the information content of species: genetic diversity, phylogeny, and conservation worth // Annu. Rev. Ecol. Syst. 1997. V. 28. P. 243–268.
De'ath G. The multinomial diversity model: linking Shannon diversity to multiple predictors // Ecology. 2012. V. 93, N 10. P. 2286–2296.
Hill M. O. Diversity and evenness: A unifying notation and its consequences // Ecology. 1973. V. 54. P. 427–431.
Hurlbert S. The Nonconcept of species diversity: A critique and alternative parameters // Ecology. 1971. V. 52. P. 577–586.
Jost L. Entropy and diversity // Oikos. 2006. V. 113. P. 363–375.
Jost L. Partitioning diversity into independent alpha and beta components // Ecology. 2007. V. 88, N 10. P. 2427–2439.
MacArthur R. H. Patterns of species diversity // Biol. Rev. 1965. V. 40. P. 510–533.
Magurran A.E. Measuring Biological Diversity. 2nd ed. Oxford: Blackwell Publ., 2004. 260 p.
Pallmann P., Schaarschmidt F., Hothorn L. et al. Assessing group differences in biodiversity by simultaneously testing a user-defined selection of diversity indices // Mol. Ecol. Resour. 2012. V. 12, N 6. P. 1068–1078.
R Development Core Team. R: A language and environment for statistical computing. R Foundation for Statistical Computing. Vienna, Austria, 2012. URL: http://www.R-project.org (accessed 5/28/2013).
Renyi A. On measures of entropy and information / Proc. 4th Symp. Math. Statist. Probabil. Berkeley: Univ. of California Press, 1961. P. 547–561.
Ricotta C., Avena G. C. An information-theoretical measure of taxonomic diversity // Acta Biotheor. 2003. V. 51. P. 35–41.
Ricotta C., Szeidl L. Towards a unifying approach to diversity measures: bridging the gap between the Shannon entropy and Rao's quadratic index // Theor. Popul. Biol. 2006. V. 70. Р. 237–243.
Vane-Wright R. I., Humphries C. J., Williams P.M. What to protect: systematics and the agony of choice // Biol. Conserv. 1991. V. 55. P. 235–254.
Shannon C. E., Weaver W. The Mathematical Theory of Communication. Urbana: Univ. Illinois Press, 1949. 117 p.
Tuomisto H. A diversity of beta diversities: straightening up a concept gone awry. P. 1. Defining beta diversity as a function of alpha and gamma diversity // Ecography. 2010a. V. 33. P. 2–22.
Tuomisto H. A diversity of beta diversities: straightening up a concept gone awry. P. 2. Quantifying beta diversity and related phenomena // Ecography. 2010b. V. 33. P. 23–45.
Tuomisto H. Commentary: Do we have a consistent terminology for species diversity? Yes, if we choose to use it // Oecologia. 2011. V. 167. P. 903–911.
Благодарности
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 07-04-96610) и в рамках программы Президиума РАН «Биологическое разнообразие» (раздел «Динамика биоразнообразия и механизмы обеспечения устойчивости биосистем»).







 © 2011 - 2026
© 2011 - 2026