Зорина А. А. Оценка флуктуирующей асимметрии на основе нормированного отклонения // Принципы экологии. 2013. № 1. С. 69–72. DOI: 10.15393/j1.art.2013.2361

Выпуск № 1

Письма в редакцию

pdf-версия статьи

574

Оценка флуктуирующей асимметрии на основе нормированного отклонения

 

Интерес к проблеме выбора подходящего способа оценки флуктуирующей асимметрии не ослабевает. Возможно, совместная дискуссия и активный обмен мнениями поможет точнее наметить пути решении данного вопроса.

Предлагая в свое время «нормированный показатель асимметрии» (Зорина, Коросов, 2007; Зорина, Коросов, 2009), мы указывали на его положительные стороны, видимо, недостаточно ясно. Прозвучавшая в печати критика данного показателя (Трубянов, 2010) позволяет вернуться к этой теме и более детально остановиться на его свойствах, вытекающих из техники расчета: «… в  работах  А. А.  Зориной  (2009)  и  А. А.  Зориной  и  А. В. Коросова (2009) предложена еще одна метрика. Остановимся на ней подробнее. Для  случая  одного  признака  показатель  выглядит  следующим  образом: fa_ij = (t(L_ij) ─ t(R_ij)), где t(L_ij) = (L_ij ─ M)/S, t(R_ij) = (R_ij ─ M)/S...  Что  такое  M  и  что  такое  S,  автор  этого показателя  не  оговаривает.  Остается  лишь  догадываться… утверждение  автора  о  том,  что распределение  данного  показателя  имеет  нормированное  нормальное распределение  неверно…» (Трубянов, 2010).

 Методику расчетов рассмотрим в среде Excel, где наглядно можно проследить последовательность вычислений показателя хотя бы для одной выборки (рис. 1).

 

 

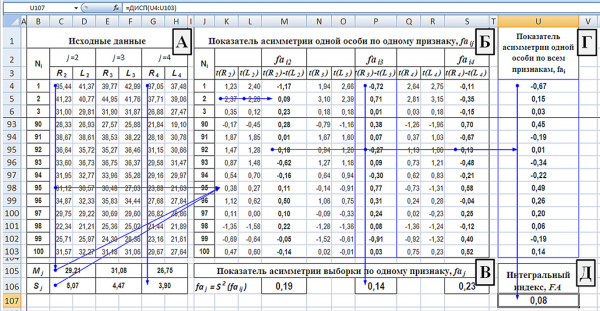
Рис. 1. Механизм расчета показателя и индекса флуктуирующей асимметрии, основанных на нормированном отклонении: в качестве исходных данных взяты промеры признаков на левой (R) и правой (L) сторонах листовой пластинки (i) березы повислой; j = 2, 3, 4 – длина второй, третьей и четвертой жилок второго порядка (Зорина, Коросов, 2009)

Fig. 1. Calculation mechanism of indicator and index of fluctuating asymmetry, based on standard deviation: measurements of signs on the left (R) and right (L) sides of the blade (i) of silver birch are taken as input data; j = 2, 3, 4 – the length of the second, third and fourth veins of the second order (Zorina, Korosov, 2009)

 

Для расчета оценок асимметрии предлагается использовать базовый способ унификации статистических данных с помощью нормированного отклонения t = (x – M) / S (Hoel, 1947). При нормировании промеров листьев используются одни и те же значения средней величины конкретного признака (M_j) и стандартного отклонения (S_j), рассчитанные по данным промеров обеих сторон. Так, значение в ячейке «K98» = (31,12 – 29,21) / 5,07 = 0,38, при этом ячейка «С105» = СРЗНАЧ(C4:D103), а «С106» = СТАНДОТКЛОН(C4:D103) (рис. 1, А). Прием, основанный на использовании постоянных значений M и S при нормировании промеров, позволяет сохранить исходную градацию величины признаков в сравниваемых группах. Вместо значений общих (рассчитанных по нескольким сравниваемым выборкам) средней и стандартного отклонения можно брать значения, рассчитанные только для одного дерева или даже для отдельной части его кроны.

После нормирования лево- и правосторонних промеров для каждой i-й особи по каждому j-му признаку вычисляется показатель асимметрии fa_ij = (t(L_ij) ─ t(R_ij)) (рис. 1, Б). Вычисляя дисперсию fa_ij для всех объектов выборки (в столбце данные по 100 листовым пластинкам) по каждому признаку получаем значения показателей асимметрии выборки по трем (в данном случае) отдельным признакам fa_j = S²(fa_ij) (рис. 1, В). Безразмерным показателем асимметрии выборки объектов выступает дисперсия разности нормированных отклонений билатеральных промеров. В данном случае процедура нормирования позволяет нивелировать значимость величины самого признака, ведь как точно заметил А. Б. Трубянов (2010): «флуктуирующей  асимметрией  …то  есть  независимым и ненаправленным и  случайными  отклонениями». Иными словами, среднее значение разности сторон достоверно от нуля не отличается, и использование нормированного отклонения оказывается более чем оправданным. Предложенная унификация  сохраняет различия в проявлении признака на левой и правой сторонах: для «симметричных» объектов (листьев) разница нормированных промеров будет близка к нулю, для «асимметричных» отличия нормированных промеров останутся большими. Поскольку обобщенная характеристика различия между сторонами определяется как дисперсия, для выборки «более асимметричных» особей (с широким размахом варьирования) получим большее значение дисперсии, нежели для выборки «более симметричных» объектов. Поэтому утверждение: «…непонятен смысл этого показателя, ведь, как было показано выше, дисперсия этого показателя есть константа» (Трубянов, 2010), скорее всего, обусловлено сложностью практического применения показателя асимметрии.

Для вычисления fa_i, усредняем отдельные значения асимметрии нормированных признаков, и для каждой листовой пластинки (если нет онтогенетически эквивалентных органов или метамеров, то данная оценка будет характеризовать целую особь) получаем интегральную оценку асимметрии по всем трем признакам: fa_i = 1/m · ∑_(j=1→m)( fa_ij) (рис. 1, Г). Процедура усреднения может вызывать сомнения: «… но ведь  у  одного  объекта  по  каким-то  признакам  может преобладать  левая  сторона,  а  по  каким-то  признакам  –  правая,  так  как  мы имеем  дело  с  флуктуирующей  асимметрией  …  вследствие  этого, отклонения  с  разными  знаками  будут  «гасить»  друг  друга  и  становится непонятен смысл данного показателя…» (Трубянов, 2010).

Однако процедура «гашения» на практике не реализуется. Чем больше признаков объекта исследования «показывают» повышение уровня асимметрии (то есть чем шире основания распределения fa_ij для каждого исследуемого признака), тем больше будет размах колебаний интегрального показателя fa_i. Иными словами, показатель, основанный на нормированном отклонении, учитывает массовые проявления флуктуирующей асимметрии у объекта изучения по нескольким признакам. Более того, процедура нормирования приводит все признаки к одинаковому диапазону изменчивости (примерно ±3) и позволяет выполнять их суммирование с признанием равной информационной значимости.

Интегральный индекс асимметрии FA получается за счет вычисления дисперсии индивидуальных показателей fa_i по всей выборке (по столбцу): FA = S²(fa_i) (рис. 1, Д). Завершающее утверждение оппонента также не соответствует действительности: «С учетом введенной автором нормировки … это значение зависит от количества  выбранных  признаков  и  не  имеет  отношения  к  оценке флуктуирующей асимметрии» (Трубянов, 2010). Итоговая величина асимметрии FA, рассчитанная по введенному показателю, не зависит от количества признаков, а характеризует качество целой выборки.

Благодарим Алексея Борисовича Трубянова  за проявленный интерес к нашей работе и высказанные замечания, которые позволили объяснить последовательность применения предложенного нами показателя и индекса флуктуирующей асимметрии.

 

Библиография