Зорина А. А. Методы статистического анализа флуктуирующей асимметрии // Принципы экологии. 2012. № 3. С. 24–47. DOI: 10.15393/j1.art.2012.1461

Выпуск № 3

Аналитический обзор

pdf-версия статьи

574

Методы статистического анализа флуктуирующей асимметрии

Введение

Определение флуктуирующей асимметрии (незначительные ненаправленные отличия в проявлении признаков на симметричных сторонах биологического объекта), также как и ее статистическая характеристика (распределение отличия сторон имеет нулевое среднее значение и подчиняется нормальному закону), говорит о стохастичном характере этого явления. Показатели асимметрии характеризуют случайную изменчивость развития в пределах нормы реакции особи и используются для характеристики «стабильности развития» и «онтогенетического шума» (Thoday, 1956; Soule, 1967; Рalmer, Strobeck, 1986, 1992; Захаров, 1987, 2000; Mitton, 1993; Рalmer, 1994). Считается, что данная форма асимметрии показывает относительную неэффективность организменных систем контроля процессов развития (Palmer, 1996; Leung, Forbes, 1997). Уровень асимметрии используют не только для описания процессов развития отдельных особей, но и их групп. Показатели асимметрии применяют при оценке состояния природных популяций в популяционной биологии (Захаров, 1987), для изучения микроэволюционных преобразований (Soule, 1967; Захаров, 2001), для определения качества среды в целях биомониторинга (Palmer, Strobeck, 1986; Методические…, 2003) и т. д. Однако результаты, получаемые при изучении закономерностей в изменении величины флуктуирующей асимметрии, нередко противоречат друг другу. Например, показатели асимметрии рекомендуется использовать в качестве индикаторов отклонения условий среды от оптимальных значений (Методические…, 2003). Считается, что чем сильнее негативное (стрессовое) воздействие, тем больше величина флуктуирующей асимметрии как в природных популяциях, так и в контролируемых лабораторных группах особей (Захаров, 1987, 2001;  Parsons, 1992; Clarke, 1993; Naugler, Leech, 1994; Kozlov et al., 1996). Однако данная закономерность не всегда подтверждается эмпирическими данными (Clarke, McKenzie, 1992; Graham, Freeman, Emlen, 1993; Manning, Chamberlain, 1993; Zvereva et al., 1997; Kellner, Alford, 2003; Гилева и др., 2007). Поэтому результаты, получаемые при анализе изменения величины асимметрии, рекомендуется подтверждать традиционными методами мониторинга состояния природных популяций и среды (Leary, Allendorf, 1989; Graham et al., 1993 ). Одна из актуальных проблем практического использования уровня флуктуирующей асимметрии — выбор нужного метода ее оценки с последующей интерпретацией получаемых на ее основе результатов (Palmer, Strobeck, 1986). В данной статье приводится краткий обзор наиболее распространенных и используемых в настоящее время показателей и индексов асимметрии, описывается их многообразие, характеризуются статистические и индикационные свойства некоторых оценок асимметрии, включая их нормальную изменчивость. 

Аналитический обзор

«Удостоверение» флуктуирующей асимметрии

Статистическая характеристика флуктуирующей асимметрии проявляется как нормальное для метрических, и биномиальное для меристических признаков распределение отличия сторон (L_ij – R_ij) с нулевым средним значением (M_{(Lij – Rij)}= 0) (рис. 1, А).  Данный тип асимметрии установлен для многих билатеральных характеристик особей, включая размеры и строение частей скелета и черепа млекопитающих (Leamy, 1992; Захаров, 2001; Гилева и др., 2007) и птиц, признаки ящериц (Гелашвили и др.,  2004) и рыб (Методические…, 2003), характеристики крыльев насекомых (Van Valen, 1962; Mason et al.,  1967), антенн диптер, губных щупальцев и сифонных сосочков пресноводных моллюсков (Palmer, Strobeck, 1986), признаки вегетативных и генеративных органов сосудистых растений (Sakai, Shimamoto, 1965; Kozlov et al.,  1996, 2002) и т. д.

 

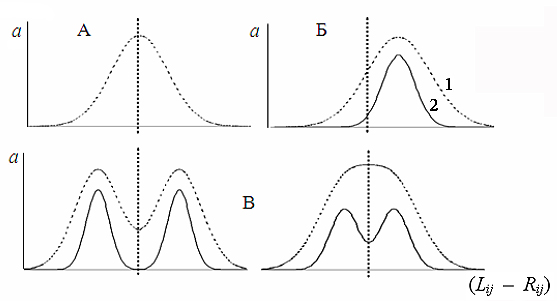
Рис. 1. Формы билатеральной асимметрии пластических признаков (Palmer, Strobeck, 1992): “A” – флуктуирующая асимметрия, “Б” – направленная асимметрия, “В” – антисимметрия; 1 – проявление фенотипа, 2 – изменчивость генотипа; a – частота. (L_ij – R_ij)  – отличие в величине j‑го признака (j = 1, 2… m) на левой (L_ij) и на правой (R_ij) сторонах тела i­-й особи (i = 1, 2… n)

Fig. 1. Forms of bilateral asymmetry of plastic signs (Palmer, Strobeck, 1992): “A” – fluctuating asymmetry, “Б” – directed asymmetry, “В” – anti-symmetry; 1 – phenotype manifestation, 2 – genotype variability; a – frequency. (L_ij – R_ij) – difference in j-sign value  (j = 1, 2… m) on the left (L_ij) and on the right (R_ij) body sides of i-individual (i = 1, 2… n)

 

В отличие от флуктуирующей, направленная асимметрия и антисимметрия имеют адаптивное значение и наследственно детерминированы. При направленной асимметрии (преобладание выраженности признака на одной из сторон тела особей в выборке) средняя арифметическая нормального (биномиального) распределения разности сторон (L_ij – R_ij) не равна нулю (M_{(Lij – Rij)} ≠ 0; рис. 1, Б). В качестве образца направленной асимметрии приводят асимметрию расположения сердца млекопитающих, лево- и правостороннюю асимметрию в строении тела камбалообразных, закрученность раковины у брюхоногих моллюсков и т. д. (Van Valen, 1962; Soule, 1967).  Антисимметрии присуще бимодальное распределение разности сторон или распределение с эксцессом меньше нормального при нулевом среднем значении M_{(Lij – Rij)} = 0 (рис. 1, В). Экстремальные формы антисимметрии можно наблюдать на примере сигнальных клешней крабов Uca sp. (Захаров, 1987; Palmer, Strobeck, 1992), когда одна клешня намного больше, чем другая, но «правши» и «левши» попадаются примерно с одинаковой частотой у всех видов.

Объединение нескольких форм асимметрий или нескольких выборок с одной и той же формой асимметрии, но разной степенью ее проявления, приводят к формированию сложных видов распределения показателя (L_ij – R_ij) (рис. 2).

 

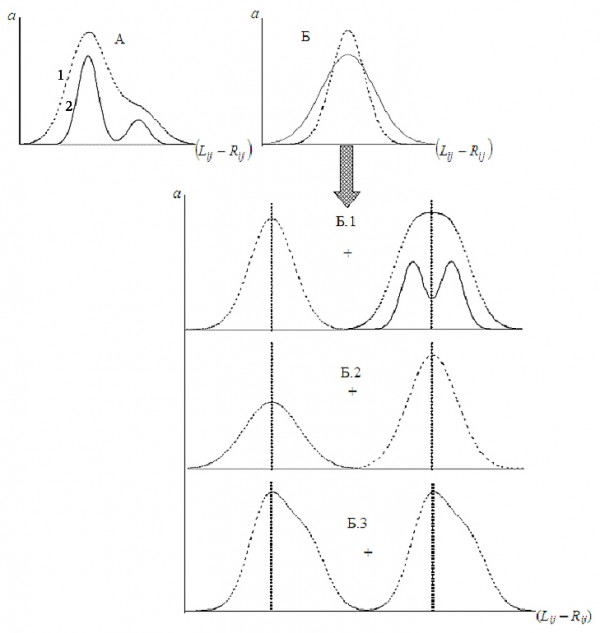
Рис. 2. Сложные виды распределения показателя отличия сторон (Palmer, Strobeck, 1992): “А” – асимметрия и “Б” –  эксцесс распределения и причины его возникновения; 1 – проявление фенотипа, 2 – изменчивость генотипа; a – частота

Fig. 2. Complicated types of distribution of side difference indicator (Palmer, Strobeck, 1992): “A” – asymmetry and “Б” – an excess of distribution and the causes of its emergence; 1 – phenotype manifestation, 2 – genotype variability; a – frequency

 

Асимметричное распределение отличия сторон может возникать, если в выборке особей с флуктуирующей асимметрией присутствует незначительная доля вариант с направленной асимметрией (рис. 2, А). Протяженность и направление скоса сложных распределений будет зависеть от величины направленной асимметрии и антисимметрии, направления асимметрий, относительной доли разных форм асимметрий в смешанной выборке.

Если признаки, распределение отличия сторон которых асимметрично или с отрицательным эксцессом, обычно исключаются из анализа, то с положительным эксцессом активно используются (Polak, 1993;  Leung, Forbes, 1997) без рассмотрения его происхождения. Тем не менее распределение показателя (L_ij – R_ij) с эксцессом больше нормального (рис. 2, Б) может проявляться как минимум в результате четырех различных причин (Palmer, Strobeck, 1992; Leung, Forbes, 1997):

1. Выборка включает две группы вариант: для первой (большинство) характерна только флуктуирующая асимметрия, для второй дополнительно отмечается наличие антисимметрии (рис. 2, Б.1).
2. Выборка включает две группы вариант: для первой характерен высокий уровень флуктуирующей асимметрии, для второй – низкий (рис. 2, Б.2).
3. Статистические особенности распределения самого признака как на левой, так и на правой сторонах тела организма (рис. 2, Б.3).
4. Высокая доля в выборке симметричных особей ((L_ij – R_ij) ≈ 0), т. е. в случае «оптимального» фенотипа.

Флуктуирующая асимметрия составляет около 1% (Palmer, 1996) от величины признака и 2—25 % (Mason et al., 1967; Зорина, 2009) от общей фенотипической его изменчивости, что затрудняет ее выявление. Более того, в общую величину изменчивости асимметрии могут вносить существенный вклад не только наличие генетически детерминированной асимметрии, но и ошибки измерения. По некоторым данным, на долю ошибки измерения метрических и меристических признаков рыб приходится 10—22 % от общей изменчивости показателей асимметрии (Ames et al., 1979), для признаков вегетативных органов березы повислой и пушистой доля составляет от 4 до 12 % (Зорина, 2009), у дентальных признаков мелких млекопитающих – до 11—25 % (Bader, 1965) и до 33—76 % у признаков пятнистости и длины крыльев бабочек нимфалид (Mason et al., 1967). Ошибки измерений сказываются на показателях асимметрии и могут служить причиной появления достоверных отличий между выборками.

 

Методические проблемы

Величина флуктуирующей асимметрии обычно очень мала по сравнению с общей фенотипической изменчивостью признаков и любая стохастичность, дополнительно привнесенная в процессе получения и обработки данных, будет оказывать значительное влияние на биологические выводы. Все разнообразие методических проблем, связанных с применением флуктуирующей асимметрии, можно свести к следующим:

1. Выбор биообъектов, их признаков и комплексов признаков.
2. Доказательство флуктуирующего характера асимметрии с последующей отбраковкой признаков.
3. Выбор показателей и индексов асимметрии.
4. Выбор параметрических или непараметрических критериев, проведение статистического анализа и интерпретация получаемых на его основе результатов.
5. Выявление закономерностей в изменении величины асимметрии. 

Выбор биообъектов, их признаков и комплексов признаков определяются в основном целями и задачами конкретного исследования. Широко используются билатеральные признаки: метрические (расстояние между фиксированными точками, длина, ширина, угол и пр.), их индексы (отношение ширины к длине и пр.), меристические (многие краниологические признаки; особенности жилкования крыльев насекомых и т.д.), качественные (наличие или отсутствие асимметричного проявления признака). Для более надежной характеристики процессов развития целого объекта используют данные по асимметрии нескольких его признаков (Van Valen, 1978; Mitton, 1993; Захаров, 2000;  Гелашвили и др., 2004; Трубянов, 2010).

При доказательстве флуктуирующего характера асимметрии признака проводят проверку на наличие других форм асимметрии, оценивают долю ошибки измерения в общей морфологической изменчивости, устанавливают зависимость величины асимметрии от размера признака. При наличии направленной асимметрии, антисимметрии или значительной доли ошибки измерения, признаки предлагается удалять из анализа флуктуирующей асимметрии. С увеличением размера объекта может увеличиваться и величина асимметрии. Сильная «размер-зависимость» оказывает влияние как на форму распределения значений асимметрии, так и на статистические характеристики выборки (Гелашвили и др., 2004), поэтому для ее учета в формулы показателей асимметрии вводят разные способы нормирования. 

Особое место занимает проблема разнообразия показателей и индексов асимметрии (способов количественной оценки величины асимметрии биообъекта). Еще в 1986 году A. R. Palmer и C. Strobeck (1986) обобщили информацию по 22 показателям асимметрии, которые свели к 9 основным. В дальнейшем число показателей асимметрии отдельных признаков и интегральных индексов асимметрии комплекса признаков значительно возросло. Нередко в одной работе применяют сразу несколько способов оценки (Pankakoski, 1985; Kimball, 1997; Kellner, Alford, 2003), результаты статистического сравнения по которым не всегда совпадают. Публикуются также специализированные обзоры существующих и предлагаемых показателей и индексов (Кожара, 1985; Zhivotovsky, 1992; Palmer, Strobeck, 2003; Гелашвили и др.,  2004).

Для установления различий между выборками и выявления закономерностей в изменении величины асимметрии часто используют сравнительный, регрессионный и корреляционный анализы. Выбор параметрических или непараметрических критериев должен определяться типом распределения используемых показателей. Иногда применяют различные дополнительные преобразования для перевода ненормально распределенных показателей в форму нормального распределения (например, логарифмические трансформации). Распределения многих показателей и индексов асимметрии, как правило, не подчиняются нормальному закону, поэтому для их сравнения приходится использовать непараметрические методы статистики (Гелашвили и др., 2004), имеющие меньшую мощность, чем параметрические (Урбах, 1964).

 

Модель изменчивости билатерального признака

 A. R. Palmer и C. Strobeck (1986, 1992) предложили простую алгебраическую модель (без учета ошибки измерения) для иллюстрации того, за какую долю фенотипической изменчивости билатерального признака отвечает флуктуирующая асимметрия:

R_ij = M_j + s_ij + D_j / 2 · A_ij + α_ij / 2 + r_ij и L_ij = M_j + s_ij – D_j / 2 · A_ij – α_ij/2 + l_ij,

где M_j = (∑R_ij + ∑L_ij) / 2n – популяционная средняя величина признака, –S_j / 2 < s_ijS_j / 2 – нормальная изменчивость размера признака (генетическая или средовая), D_j = (∑_(i=1→n)(L_ij – R_ij)) / n – популяционная оценка направленной асимметрии и ее изменчивости α_ij, A_ij – уровень антисимметрии, который имеет значение от +1 до –1 с вероятностью p (может изменяться от 0 до 1) и q = 1 – p.

Когда антисимметрия отсутствует, p = 1, когда антисимметрия присутствует и соотношение особей с преобладанием L и R примерно одинаково, тогда p = q = 0.5 и т. д. Отсюда среднее значение M(A_ij) = 2p – 1 с бимодальной генетической или средовой изменчивостью S(A_ij) = 4pq. Индексы r_ij и l_ij характеризуют процессы развития правой и левой сторон.

При наличии зависимости между величиной флуктуирующей асимметрии и размером признака, модель будет выглядеть следующим образом:

R_ij = M_j + s_ij + D_j / 2 · A_ij + α_ij / 2 + (K(M_j + s_ij)(r_ij)) и L_ij = M_j + s_ij – D_j / 2 · A_ij – α_ij / 2 + (K(M_j + s_ij)(l_ij)),

где К – константа пропорциональности.

Формула дает возможность наглядно представить компоненты изменчивости, которые будут входить в величину разности сторон (R_ij – L_ij) = D_jA_ij + α_ij + r_ij – l_ij. Следует отметить, что при введении поправки на направленность асимметрии сохраняется соответствующая ей компонента α_ij. При отсутствии генетически детерминированных форм асимметрий, показатель отличия сторон будет характеризовать только флуктуирующую асимметрию. При наличии «масштабного эффекта» показатель разности сторон будет включать зависимость уровня асимметрии от величины признака (R_ij – L_ij) = [K(M_j + s_ij)( r_ij – l_ij)].

В моделях представлены все основные компоненты фенотипической изменчивости, которые могут оказывать влияние на распределение показателя отличия сторон, кроме ошибки измерения. Флуктуирующая асимметрия пластических признаков обнаруживается в форме нормального распределения разности между промерами сторон признака (R_ij– L_ij), при этом показатели асимметрии, эксцесса и среднее значение равны нулю (Van Valen, 1962). Для проверки распределения на нормальность предлагается использовать несколько критериев, например, Колмогорова – Смирнова или χ² Пирсона, а при проверке на значимость эксцесса и антисимметрии – t-Стьюдента. Для выявления направленной асимметрии можно провести сравнение величины признака на левой и правой сторонах.  В случае нормального распределения признака используют, например, критерий t-Стьюдента. Если распределение признаков не подчиняется нормальному закону, то сравнение проводят с помощью непараметрических критериев (Уилкоксона – Манна – Уитни, Уайта и т. д.). Также возможно сравнение левой и правой сторон по частотному распределению признака, например с применением критерия χ². Индикатором антисимметрии служит отрицательный эксцесс или бимодальность (Palmer, Strobeck, 1992; Developmental…, 2003; Гелашвили и др., 2004).

Другой способ верификации флуктуирующего характера асимметрии основан на анализе морфологической изменчивости билатерального признака и заключается в декомпозиции ее дисперсии с помощью дисперсионного анализа или теста ANOVA. A. R. Palmer и C. Strobeck (1986) подробно рассмотрели процесс декомпозиции для случаев, когда есть возможность оценить все компоненты изменчивости, то есть когда стабильность развития одного и того же генотипа может быть оценена по нескольким онтогенетически эквивалентным особям или частям (несколько оценок отличия сторон для одного и того же генотипа). Такое возможно в двух случаях: 1) когда несколько особей имеют идентичный генотип, что происходит при образовании клонов у партеногенетических особей (редкое явление); 2) когда у особи присутствуют два или более гомологичных органов (колониальные беспозвоночные или растения).

Модель общей изменчивости морфологического признака растений с несколькими онтогенетически эквивалентными органами – метамерами (например, листья, иголки и т. д.) имеет следующие компоненты:

MS_общ.= MS_г + MS_с + MS_внутри,

где MS – это соответствующая компонента дисперсии (средний квадрат) или S².

Достоверное влияние фактора «сторона» (MS_с) свидетельствует о направленной асимметрии. Значимость фактора «генотип» (MS_г) говорит о влиянии размера признака (особи) на величину отличия сторон, что указывает на необходимость учитывать масштабный эффект. Достоверное взаимодействие между факторами (MS_гс) указывает на наличие антисимметрии. Случайная компонента дисперсии MS_внутри и представляет собой флуктуирующую асимметрию. Получается, что в рамках теста ANOVA проводится анализ компонентов морфологической изменчивости, характеристика их соотношения и значимости, а также оценка самой флуктуирующей асимметрии MS_внутри = fa_j. Сравнение выборок по данному показателю асимметрии группы особей по одному признаку, проводится с помощью параметрического критерия Фишера. A. R. Palmer и C. Strobeck (1986) отмечают высокую точность и надежность данного показателя (наиболее высокую из 22 рассмотренных ими способов оценки асимметрии) при выявлении отличий между выборками.

Однако у большинства организмов (особенно животных) нет идентичных органов, на основе которых можно было бы получить несколько оценок показателя отличия сторон признака (R_ij– L_ij) для характеристики одного и того же генотипа. В случае когда один генотип соответствует одной особи и одной оценке разности между промерами сторон признака, для характеристики компонентов морфологической изменчивости признака используется двухфакторный дисперсионный анализ без повторностей:

MS_общ.= MS_г + MS_с + MS_{погрешн}. Изменчивость, обусловленная взаимодействием факторов, будет объединена со случайной компонентой дисперсии, и для выявления антисимметрии потребуются дополнительный анализ распределения показателя отличия сторон (в частности, проверка на значимость эксцесса или бимодальности). Если антисимметрия не будет доказана, показателем флуктуирующей асимметрии выступит компонента дисперсии «погрешность» MS_{погрешн} = fa_j.

Если есть повторные промеры признака на каждой стороне, то с помощью дисперсионного анализа также можно оценить долю изменчивости, которая приходится на ошибку измерения. При этом формируется таблица двухфакторного равномерного дисперсионного комплекса с двукратной повторностью (повторные промеры признака на каждой стороне). Таблица включает две градации по фактору «сторона» (левая и правая стороны) и n (количество особей в выборке) градаций по фактору «генотип». Тогда декомпозиция общей морфологической изменчивости признака примет следующий вид:  MS_общ.= MS_г + MS_с + MS_взаим + MS_внутри. При этом показателем флуктуирующей асимметрии выступает дисперсия, обусловленная взаимодействием факторов MS_взаим = fa_j (если нет антисимметрии), а ошибка измерения представляет собой корень квадратный из случайной компоненты дисперсии √(MS_внутри) = ОИ_j (Гилева и др.,  2007).

Для того чтобы понять, какая доля в изменчивости показателя асимметрии имеет методическую природу, а какая действительно обусловлена биологически, ошибки измерения рекомендуется оценивать в каждом исследовании. О значимости ошибки измерения обычно судят по отношению показателей асимметрии fa_j и ошибки ОИ_j. Согласно A. R. Palmer и C. Strobeck (2003) необходимо, чтобы средняя абсолютная разность между промерами сторон признака превышала ошибку измерения хотя бы двукратно. Ошибку предлагается отнимать от оценок асимметрии (Palmer, Strobeck, 1986). Другие исследователи считают, что величина ошибки измерения «укладывается в рамки допустимого», если между двумя выборками показателей асимметрии, полученными на основе повторных промеров, нет достоверных отличий (Swaddle, Witter, 1997). Иногда для оценки значимости ошибки измерения вычисляют коэффициент корреляции между выборками повторных промеров, высокая величина которого (r > 0.95) считается удовлетворительной для обычной (нормы) ошибки (Mason et al., 1967).

 

Многообразие показателей асимметрии

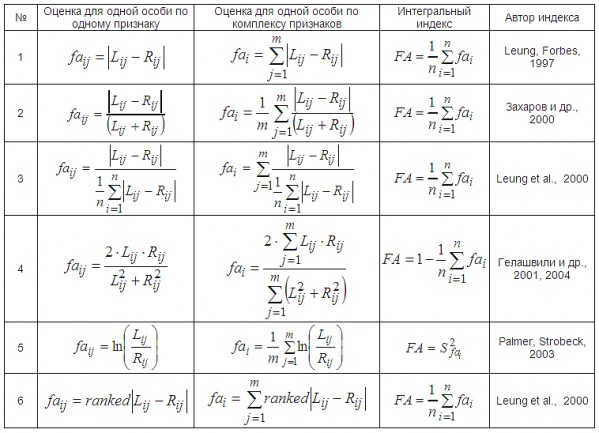
 Рассмотренный выше способ оценки асимметрии с помощью дисперсионного анализа характеризует уровень асимметрии группы особей по одному признаку. В целом представленные в литературе показатели условно можно разбить для наглядности и простоты понимания на четыре иерархических уровня: 1 – оценки флуктуирующей асимметрии у отдельной особи (варианты) по одному  признаку, 2 – оценки асимметрии для группы (выборки) особей по одному  признаку, 3 – оценки асимметрии у отдельной особи по комплексу признаков (комплексные показатели асимметрии) и 4 – оценки асимметрии для группы (выборки) особей по комплексу  признаков (интегральные индексы). Все они характеризуют изменчивость, т. к. средняя величина для значений разности между билатеральными промерами равна нулю. При расчете показателей и индексов используется большое количество способов преобразования исходных данных (значений признаков на левой и правой сторонах тела особей), включая модуль, возведение в квадрат, логарифмирование и т. д. (табл. 1). 

 

Таблица 1. Показатели флуктуирующей асимметрии отдельной особи по одному  признаку

Table 1. The indicators of fluctuating asymmetry of an individual based on one sign

(Palmer, Strobeck, 1986; Zhivotovsky, 1992; Leung et al.,  2000; Developmental …, 2003)

 

Структура формулы оценки асимметрии одного признака у отдельной особи определяется  выбором показателя отличия сторон d_ij= L_ij – R_ij (просто разница между сторонами, абсолютное отличие сторон или деление величины признака одной стороны на другую) и способом нормирования (деление на величину признака, логарифмирование и пр.). Когда сам показатель отличия сторон выступает оценкой асимметрии (табл. 1: 1), нормирование не используется: fa_ij = d_ij.

При изучении флуктуирующей асимметрии особо отмечается проблема «масштабного эффекта». Корреляцию между размером признака и величиной асимметрии пытаются учесть с помощью различных способов нормирования, среди которых используют деление показателя асимметрии особи на величину промера или логарифмирование значений: fa_ij = d_ij / x_ij, где процедура деления на x_ij характеризует нормирование на размер признака отдельной особи, например деление на x_ij = (L_ij + R_ij) / 2 или на x_ij = (L_ij + R_ij) (табл. 1: 2).

Отличия выборок по величине и изменчивости признаков может оказывать влияние на изменчивость показателей асимметрии. Нормирование на среднюю величину размера признака в выборке компенсирует «масштабный эффект» выборок: fa_ij = d_ij / M. Величина M в знаменателе характеризует нормирование на среднюю величину размера признака в выборке (учет отличий между группами особей по величине признака), например M = M_j или M = M_Rj, где M_j = 1 / (2n)∙ ∑_{(i=1 → n)}(L_ij + R_ij) = 1 / n ∙ ∑_{(i=1 → n)}(x_ij) и M(R_j) = 1 / n ∙ ∑_{(i=1 → n)}(R_ij) (табл. 1: 3).

Величина флуктуирующей асимметрии одного признака в той или иной мере отличается от величины показателя для другого признака.  Для компенсации отличий между показателями асимметрии разных признаков нормирование проводят путем деления величины асимметрии отдельной особи по одному признаку на общую характеристику признака или его асимметрии в выборке: fa_ij = d_ij / S или fa_ij = d_ij / M(fa_j), где S используется для нормирования на общую изменчивость признака в выборке (или стандартное отклонение, или дисперсия), а M_fa характеризует нормирование на средний уровень асимметрии признака, рассчитанный по всем выборкам, участвующим в сравнении M(fa_j) = 1 / N ∙ ∑_{(i=1 → N)}(fa_ij) (табл. 1: 4).

Структура формулы показателя асимметрии одного признака у группы (выборки) особей (групповые показатели fa_j) определяется формой показателя асимметрии для отдельной особи (fa_ij) и представляет собой сумму, среднюю величину значений fa_ij для всех особей выборки или характеристику изменчивости распределения индивидуальных показателей (дисперсия, стандартное отклонение). Если оценка асимметрии отдельной особи по одному признаку основана на модуле отличия сторон (d_ij = |L_ij – R_ij|), то групповой показатель асимметрии представляет собой суммирование индивидуальных оценок асимметрии всех особей выборки fa_j = ∑_{(i=1 → n)}(fa_ij) или усреднение fa_j = 1 / n ∙ ∑_{(i=1 → n)}(fa_ij). Для случая обычной разности между сторонами (с сохранением знака – d_ij = (L_ij – R_ij)) форма групповой оценки определяется типом распределения индивидуального показателя. В случае нормального распределения показателя fa_ij, оценивается его изменчивость для выборки особей в виде стандартного отклонения fa_j = S(fa_ij) или дисперсии fa_j = S²(fa_ij) или fa_j = 1 / 2 ∙ S²(fa_ij) (иногда оценка изменчивости умножается на 100 %). Иногда групповой показатель усложняют, вводя в формулу процедуру деление дисперсии асимметрии на среднюю характеристику величины признака в выборке

fa_j = S²(fa_ij) / M²(j) или fa_j = S²(fa_ij) / M(j) (Developmental…, 2003). Когда показатель fa_ij не подчиняется нормальному закону, оценки асимметрии по выборке особей просто усредняются fa_j = 1 / n ∙ ∑_{(i=1 → n)}(fa_ij), например fa_j = 1 / n ∙ ∑_{(i=1 → n)}(L_ij – R_ij)² или fa_j = 1 / n ∙ ∑_{(i=1 → n)}((L_ij – R_ij) / M(R_j)) ∙ 100 %. Если для расчета индивидуальной оценки асимметрии используют показатель отличия сторон в виде их отношения друг к другу (L_ij / R_ij) или логарифмирования, то групповой оценкой асимметрии признака выступает дисперсия fa_j = S²(fa_ij).

Непосредственная оценка группового показателя асимметрии признака без предварительного расчета величины асимметрии отдельно для каждой особи была рассмотрена нами в предыдущем разделе при декомпозиции общей изменчивости морфологического признака с помощью дисперсионного анализа. Еще один подобный пример – коэффициент корреляции между величиной признака на левой и правой сторонах тела особей fa_j = r и различные его модификации, например, fa_j = 1 – r или fa_j = 1 – r². Если показатель асимметрии, вычисляемый как компонента дисперсии, используется достаточно часто, то групповой показатель асимметрии в виде коэффициента корреляции в последнее время практически не используется (Palmer, Strobeck, 1986).

Групповые оценки асимметрии отдельных признаков (fa_j) редко сами участвуют при проведении сравнения. Обычно различия между выборками устанавливаются при сопоставлении двух распределений fa_ij с помощью непараметрических критериев (Developmental…, 2003; Гелашвили и др., 2004) или с использованием критерия t‑Стьюдента (Захаров и др.,  2000). Исключения составляют показатели fa_j в виде дисперсии или стандартного отклонения, которые могут непосредственно использоваться при сравнении выборок с помощью критерия Фишера. Основное применение оценки асимметрии для группы особей по одному признаку (fa_j) находят при исследовании согласованности в изменении асимметрий признаков по разным группам, при разработке балльных шкал, определении условной нормы, критических порогов, выявлении трендов и установлении моделей изменчивости показателей асимметрии.

Для характеристики согласованной изменчивости групповых оценок асимметрии разных признаков применяется коэффициент W конкордации Кендала (Soule, 1967; Mason, 1967), для вычисления которого показатели асимметрии ранжируют (fa_j = R_kj, где k – количество выборок, участвующих в анализе, для каждой из которых рассчитана оценка fa_j). Пример ранжированных групповых оценок асимметрий представлен в таблице 2.

 

Таблица 2. Ранги групповых показателей асимметрий для расчета коэффициента конкордации

Table 2. The ranks of group indicators of asymmetry for the calculation of a concordance index

 

Коэффициент конкордации Кендала рассчитывается по формуле

W = (12 ∙ ∑d²) / (m² ∙ (N³ – N)),  где d_k = ∑_(j=1→m)(R_k) – 1 / N ∙ ∑_(k=1→N)(∑_(j=1→m)R_k).

 Значения коэффициента варьирует в пределах от 0 (нет согласованности между показателями асимметрии разных признаков) до 1. Обычно о сильной согласованности в изменчивости показателей асимметрии признаков говорят, когда коэффициент не ниже 0.6, однако в силу малого количества групповых оценок, используемых в анализе (редко больше десяти групп особей или популяций), о статистической значимости коэффициента судят по критерию χ² = m ∙ (N – 1) ∙ W (Mason, 1967). Если эмпирическая величина критерия больше теоретического значения χ²_(0.05,N-2), то говорят о согласованной изменчивости показателей асимметрии признаков по группам особей. Достоверность коэффициента W может означать, что оценки асимметрии разных признаков биообъектов отражают один определенный феномен, лежащий в основе изменчивости процессов развития разных выборок (популяций). Таким феноменом может выступать всеобщая коадаптация генетических элементов (Soule, 1967), отличия в генотипической структуре популяций (Palmer, Strobeck, 1986), изменчивость метаболической эффективности (Захаров, 1987), разная степень онтогенетического шума (Palmer, Strobeck, 1986).

Иногда коэффициент конкордации Кендала используется для установления согласованности в изменчивости оценок асимметрии разных признаков в пределах группы особей; в этом случае ранжируются индивидуальные показатели асимметрии fa_ij = R_ij. С помощью этого теста было доказано отсутствие «общеорганизменного свойства асимметрии» (Van Valen, 1962; Mason et al., 1967; Leamy, 1992).

 

Интегральные индексы

 Разработка и использование интегральных индексов асимметрии выборки особей по комплексу признаков ведутся с 80-х гг. XX в. Предполагается, что подобные комплексные показатели точнее и надежнее характеризуют процессы развития целого объекта (отдельную особь или популяцию), повышают вероятность выявления закономерностей в изменчивости асимметрии биообъектов, позволяют детальнее изучить влияние факторов на реализацию процессов развития (Zhivotovsky, 1992; Leung et al.,  2000; Гелашвили и др.,  2004).

Структура формулы интегрального индекса зависит от формы показателя асимметрии для отдельной особи по одному признаку (табл. 1), а также от способа объединения показателей асимметрии отдельных признаков в новый (сложный) признак, который будет характеризовать одну особь по комплексу свойств. Оценки асимметрии всех m признаков у одной особи (fa_i) усредняются или просто суммируются. Для расчета интегрального индекса FA асимметрии комплекса признаков для группы (выборки) особей используются усреднение, суммирование, вычисление дисперсии или стандартного отклонения распределения показателей fa_i (табл. 3). Д. Б. Гелашвили (Гелашвили и др., 2004) при вычислении индекса асимметрии предлагает проводить одновременно и суммирование, и нормирование отличий между сторонами по всем признакам (табл. 3: 4). B. Leung (2000) акцентирует внимание на отличии признаков друг от друга по процессам стабильности развития. Для того чтобы признаки оказывали равноценный вклад в интегральную оценку, при расчете индивидуальных показателей автор вводит нормирование на среднюю величину асимметрии признака в выборке (табл. 3: 3). B. Leung (2000) также считает, что одним из наиболее надежных способов учета отличий между асимметриями разных признаков выступает ранжирование оценок асимметрий по каждому признаку с последующим суммированием рангов (табл. 3: 6).

 

Таблица 3. Оценки флуктуирующей асимметрии по комплексу признаков

Table 3. The estimates of fluctuating asymmetry based on a signs complex

 

Представленные формулы позволяют рассчитывать комплексные показатели асимметрии у отдельных особей по нескольким признакам. Сравнение выборок обычно проводится с помощью непараметрических критериев, когда сопоставляются распределения  показателей fa_i двух выборок (Гелашвили и др., 2004), реже предлагается использовать критерий t‑Стьюдента и тест-ANOVA (Leung et al., 2000).

Принципиально иной способ оценки интегральных индексов основан на применении разных методов многомерного анализа. Например, L. A. Zhivotovsky (1992) предлагает алгоритм вычисления «обобщенной изменчивости асимметрии» комплекса признаков FA = G ∙ (detS)^1/k. При расчете детерминант (detS) для каждой выборки создается матрица «изменчивость – ковариация», включающая показатели асимметрии всех признаков. L. A. Zhivotovsky приводит формулы поправочного коэффициента G и краткую таблицу уровней G при определенном числе степеней свободы. Сравнение выборок проводится с помощью F-теста. Однако, A. R. Palmer (1994) отмечает сложность предыдущего показателя и предлагает обычный двухфакторный дисперсионный анализ в качестве альтернативы.

Среди новых работ следует отметить недавно предложенный подход, определяющий степень  псевдосимметричности (приблизительной симметрии) биообъектов на основе теории групп (Гелашвили и др., 2010; Нижегородцев, 2010). Метод учитывает не только разные типы асимметрии билатеральных признаков, но и включает другие возможные преобразования (повороты,  инверсии,  трансляции  и  др.).  Авторы разработали комплекс программных продуктов BioPs для автоматической оценки степени псевдосимметрии биообъектов на  основе  алгоритма  свертки. В расчетах используются числа, задающие яркости пикселов цифрового изображения объектов. Выражение  интегральной  свертки,  предложенной  Гелашвили  и  др.  (2004)  для  оценки псевдосимметрии  приобретает вид конечной суммы:

η = ∑_(i,j)(A_i,j ∙ B_i,j) / ∑_(i,j)(A²_i,j), где η – степень  симметричности,  A  –  матрица  яркостей  исходного  изображения,  В  – матрица  яркостей,  полученная  в  результате отражения  матрицы  A  относительно выбранной плоскости.

 

Показатели асимметрии неметрических  признаков

 В соответствии с распространенной классификацией признаков (Животовский, 1991), к качественным относят те свойства (вариации, морфы, фенотипы и т. д.), при использовании которых совокупность особей можно однозначно разделить на четко различимые группы. Количественными называются признаки, степень выраженности которых можно охарактеризовать числом. Выделяют три типа количественных признаков. Дискретные признаки (счетные или меристические) определяются путем подсчета (число позвонков у рыб, щетинок у мух, пульс и т. д.). Непрерывные признаки (метрические, пластические) определяются путем измерений (размеры и вес особей, активность ферментов и т. д.). Для меристического признака величина асимметрии определяется по различию числа структур слева и справа, а для качественного свойства просто учитывается симметрично или асимметрично проявление признака. Обзор литературы показал, что те показатели, которые применяются для характеристики флуктуирующей асимметрии пластических признаков, также используются и для неметрических признаков организмов.

Один из немногих примеров разграничения оценок асимметрии по типу признака можно найти в работах A. R. Palmer и C. Strobeck (2003). В частности, они особо отмечают показатели, основанные на «дискретизированном» значении асимметрии (b_ij = 0, если L_ij = R_ij, b_ij = 1, если L_ij ≠ R_ij), и предлагают их использовать только при оценке асимметрии неметрических признаков. Групповым показателем в данном случае выступает усредненная величина асимметричного проявления признака в выборке fa_j = 1 / n ∙ ∑_(i=1→n)(b_ij) (Захаров, 2000). В качестве комплексного показателя асимметрии особи по нескольким признакам рассчитывается средняя величина асимметрично проявившихся признаков у одной особи fa_i = 1 / m ∙ ∑_(j=1→m)(b_ij), а формула интегрального индекса будет включать двойное усреднение:

FA = (1 / (n ∙ m)) ∙ ∑_(i=1→n)(∑_(j=1→m)(b_ij)) = 1 / n ∙ ∑_(i=1→n)(fa_i) (Захаров, 2000; Гелашвили и др.,  2004). A. R. Palmer и C. Strobeck (2003) предлагают вместо процедуры усреднения использовать простое суммирование при расчете показателя асимметрии особи по комплексу признаков.

Другая оценка асимметрии предложена А. Г. Васильевым (2007) на основе формул R. R. Sokal и P. H. A. Sneath (1973). Формулы позволяют вычислить дисперсию общей асимметричности, которую А. Г. Васильев обозначил ТА², и двух ее компонент: DA² – направленную и FA² – флуктуирующую асимметрии (Васильев и др., 2007). Дисперсию общей асимметричности комплекса признаков для отдельной особи предложено вычислять по формуле ТА² = 1 / m ∙ ∑_(j=1→m)(L_ij – R_ij)². Дисперсия направленной асимметрии будет равна:

DА² = 1 / m²∙[∑_(j=1→m)(L_ij – R_ij)]², тогда вторая компонента – флуктуирующая асимметрия вычисляется так: FА² = TА² – DА². Однако, несмотря на то, что данные показатели апробированы только на  дискретных признаках, предлагается их более широкое применение (Васильев и др.,  2007).

 

Анализ работоспособности показателей и индексов

 Многообразие показателей асимметрии создает проблему выбора способа оценки для конкретного исследования. Какому показателю следует отдать предпочтение и каковы преимущества той или иной оценки? В ряде работ проводятся сравнения показателей друг с другом, анализируются их свойства и работоспособность, которые позволяют провести ранжирование в порядке убывания их «качества».

В основном исследования направлены на анализ чувствительности показателей, т. е. их способности улавливать реальные отличия по величине асимметрии между выборками (анализ индикационных способностей). Оценка работоспособности показателей проведена в рамках имитационных моделей на искусственно созданных данных. Например, A. R. Palmer и C. Strobeck (1986) при характеристике относительной чувствительности девяти индексов наблюдали изменение точности показателей асимметрии при изменении таких факторов, как фенотипическая изменчивость признака, направленная асимметрия, антисимметрия, степень зависимости величины флуктуирующей асимметрии от размера признака. Способность каждого показателя выявлять отличия между выборками они оценивали с помощью дисперсионного анализа логарифмированных переменных.

A. R. Palmer и C. Strobeck (1986) установили, что индексы, основанные на коэффициенте корреляции, проявляют высокую чувствительность к изменению величины признака и поэтому неэффективны. При отсутствии «масштабного эффекта», наилучшей работоспособностью обладают оценки, основанные на обычном показателе отличия сторон (L_ij – R_ij) и его дисперсии. При увеличении зависимости уровня асимметрии от размера признака, более надежными становятся оценки, которые также основаны на показателе (L_ij – R_ij), только с учетом масштабного эффекта, например вида fa_ij = 2 ∙ (L_ij – R_ij) / (L_ij + R_ij).  A. R. Palmer и C. Strobeck (1986) подчеркивают большую эффективность оценок на основе разности между сторонами (L_ij – R_ij) по сравнению с абсолютными отличиями |L_ij – R_ij|.

B. Leung (2000) на основе имитационного моделирования сделал попытку оценить свойства интегральных индексов. Работоспособность индексов он проверяет по двум критериям: 1 – достоверность отличий между выборками, которые взяты из одной генеральной совокупности (правомерность применения индекса за счет учета ошибки первого рода); 2 – значимость отличий между выборками, которые взяты из разных генеральных совокупностей (оценка силы или чувствительности индекса). Было показано, что интегральные индексы, учитывающие несколько признаков, обладают большей чувствительностью по сравнению с выборочными показателями, оценивающими асимметрию отдельного признака. «Сила» индексов зависит от количества признаков, входящих в состав индекса, от размера выборки особей, от степени отклонения распределений показателей асимметрии отдельных признаков от нормального закона, от ошибки измерения. При увеличении согласованности в изменении показателей асимметрии признаков в пределах выборки чувствительность индексов уменьшается. На повышение вероятности появления ошибки первого рода могут оказывать влияние положительный эксцесс распределения показателей асимметрии отдельных признаков, наличие корреляции между показателями асимметрии разных признаков. Из всего разнообразия интегральных индексов B. Leung (2000) отдает предпочтение тем, при расчете которых индивидуальные оценки включают нормирование на средний уровень асимметрии признака в выборке или ранжирование показателей асимметрии по каждому признаку.

Рассмотренные работы по анализу работоспособности показателей и индексов асимметрии проводятся на основе модельных выборок с заранее заданными распределениями и известными параметрами. Появляются работы по оценке чувствительности показателей и анализу их статистических свойств с использованием значительного объема эмпирического материала (Зорина, Коросов 2009; Зорина, 2009; Трубянов, 2010; Трубянов, Глотов, 2010). В таблице 4 представлены наиболее отличающиеся друг от друга показатели и индексы флуктуирующей асимметрии, которые часто используются в работах по исследованию качества среды в целях биомониторинга или введены в последнее время.

 

Таблица 4. Формулы расчета оценок флуктуирующей асимметрии, используемых в сравнении

Table 4. The formulas for the calculation of the estimates of fluctuating asymmetrybsed in comparison

*Примечание к таблице 4: M_j и S_j – средняя арифметическая и стандартное отклонение j-го билатерального признака по всем выборкам, участвующим в сравнении, N – суммарный объем выборок (N=n₁+…+n_x).

 

Простейшая оценка флуктуирующей асимметрии отдельного билатерального признака представляет собой дисперсию разности сторон fa_j(1) = S²(L_ij – R_ij) (Кожара, 1985; Palmer, Strobeck, 1992). Формулы показателей fa_ij(3), fa_ij(4), fa_ij(5), fa_ij(6), fa_ij(7), fa_ij(8), fa_ij(9) и соответствующих индексов, представленные в литературе (Palmer, Strobeck, 1986, 2003; Zhivotovsky, 1992; Leung et al, 2000; Захаров, 2001; Гелашвили и др., 2004; Зорина, Коросов, 2009), используют различные преобразования для перевода промеров признаков или их билатеральной разности в относительные величины.

С технической точки зрения расчеты всех показателей и индексов выполняются в несколько этапов. Сначала для каждой i-й особи по каждому j-му признаку вычисляют  отличие сторон fa_ij. Усредняя значения fa_ij (или вычисляя дисперсию) для всех особей выборки (в столбце) по каждому признаку, получают свой показатель асимметрии fa_j. Усредняя значения fa_ij для всех признаков данной особи (в строке), получают интегральную оценку асимметрии fa_i для каждой особи. Усредняя индивидуальные оценки fa_i (или вычисляя дисперсию) по всей выборке особей (в столбце), получают интегральный индекс асимметрии FA для всех особей по всем признакам.

Итоги сравнения работоспособности оценок асимметрии показали, что на основании одних и тех же данных разные показатели асимметрии могут давать разные результаты (Зорина, Коросов, 2009; Зорина, 2009). Одна из возможных причин – отличие форм распределения оценок асимметрии, что наблюдается при изучении нормальной изменчивости показателей или индексов. На этой основе строится весь последующий статистический анализ — выбор  непараметрических или параметрических критериев и выявление закономерностей. Изучение статистических свойств и закономерностей нормальной изменчивости показателей и индексов флуктуирующей асимметрии признаков биообъектов проводилось на основе использования «чистых» выборок растений и животных, характеризующихся значительными объемами и относительной однородностью материала.

Изначально нормальное распределение разности сторон (L_ij – R_ij) признаков сохраняется для показателей fa_ij(4), fa_ij(5), fa_ij(7), fa_ij(9); распределение остальных оценок (fa_ij(2), fa_ij(3), fa_ij(6), fa_ij(8)) не подчиняется нормальному закону. Модуль разности |L_ij – R_ij|, использованный в формулах 2, 3 и 6 (табл. 4) превращает все отклонения билатеральных промеров в положительные и приводит их распределение к правосторонней асимметрии (рис. 3: 2, 3, 6). Для преобразования абсолютной разности |L_ij – R_ij| в разряд относительных показателей, выражающих пропорции (fa_ij(6)), применяется деление на сумму промеров |L_ij – R_ij| / (L_ij + R_ij). Распределению подобных относительных индексов присуще нарушение симметрии (Шварц и др., 1968) и приближение к форме логнормального (Дэвис, 1977) (рис. 3: 6). К похожему эффекту ведет возведение в квадрат (Тьюки, 1981): большие значения случайной величины возрастают сильнее небольших и обеспечивают положительную асимметрию распределению. Если же квадрат стоит в знаменателе показателя (fa_ij(8)), получим обратный результат – левостороннюю асимметрию (рис. 3: 8).

 

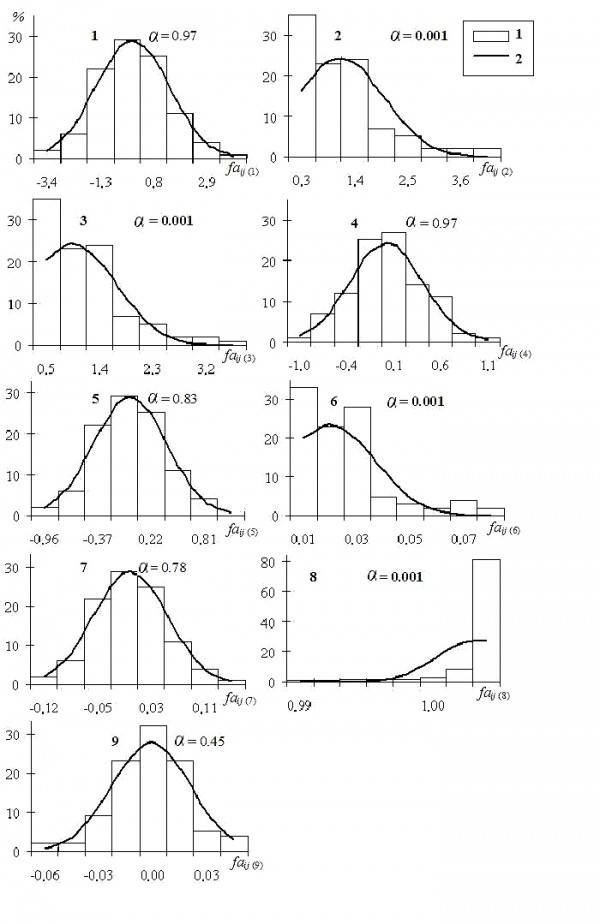
Рис. 3. Эмпирические частоты распределения показателей асимметрии (fa_ij) метрического признака листовой пластинки березы повислой (1) и кривые нормального распределения с теми же параметрами (2) (указан уровень значимости соответствия нормальному закону по критерию W Шапиро – Уилкса)

Fig. 3. The mpirical frequencies of asymmetry indicator distributions (fa_ij) of metric sign of Bétula péndula leave plate (1) and the curves of normal distribution with the same parameters (2) (the significance value of compliance with the normal law according to the  W  Shapiro – Wilks criterion  is specified)

 

Одно из последствий нарушения исходного нормального распределения билатеральной разности (L_ij – R_ij) показателями fa_ij(2), fa_ij(3), fa_ij(6), fa_ij(8) – это запрет на сравнение выборочных значений с помощью точных параметрических критериев. Более того, показатели с ненормальным распределением переносят незначительные отличия между выборками на одну сторону гистограммы и усиливают их (Зорина, Коросов, 2009). Они повышают значимость редких случайных отклонений и выдают их за существенные (включая методические огрехи).

Наконец, сам способ нормирования может привнести дополнительную компоненту изменчивости в уровень асимметрии, и отличия между выборками будут иметь совершенно иную природу происхождения (не связанную с нарушением онтогенеза особей). Один из примеров – это когда разность промеров делится на их сумму, т. е. характеристика изменчивости относится к характеристике величины признака (некий аналог коэффициента вариации) в показателях fa_ij(6), fa_ij(7), fa_ij(8), fa_ij(9). Поскольку между дисперсией и средней величиной морфологических признаков нет однозначной зависимости (Яблоков, 1966), то появляется еще одна компонента, закономерности изменчивости которой отдельно не обсуждаются, но которая вводится в оценку уровня асимметрии признака. То же самое касается нормирования на характеристику изменчивости признака (в частности, на стандартное отклонение распределения билатерального признака в показателе fa_ij(5)). Зависимость между фенотипической изменчивостью признака и показателем отличия сторон (L_ij – R_ij) носит сложный неоднозначных характер (Кожара, 1985; Palmer, Strobeck, 2003). Нормирование может приводить к отличиям между выборками, которые сложно интерпретировать.

Считается, что флуктуирующую асимметрию целого объекта полнее характеризуют интегральные индексы, и их сравнение позволяет делать более надежные выводы, чем при анализе отдельных признаков (Developmental …, 2003). Однако в большинстве случаев индексы рассчитываются путем простого объединения показателей асимметрии отдельных признаков и сохраняют их недостатки, например нарушение нормального распределения. Есть вопросы и к способу расчета индексов FA, которым рекомендуется простое усреднение значений fa_ij (табл. 4), тогда как при объединении асимметричных распределений наиболее представительной и устойчивой характеристикой выступает медиана (Животовский, 1991).

Индексы никак не учитывают различие статистических характеристик показателей асимметрии отдельных промеров – значения частных показателей просто усредняются для каждой особи. Разные признаки имеют разную форму распределений и разные уровни статистических параметров. Их объединение означает, что наибольшую роль в общей средней особи будут играть только те показатели асимметрии, которые имеют самые большие значения.

Вопрос о правомочности процедуры усреднения относительных показателей асимметрии для m разных исходных признаков актуален и для оценок fa_i(5), fa_i(7), fa_i(9) (табл. 4). Для расчета величин данных показателей используются нормированные значения fa_ij, которые в силу безразмерности усредняются. При этом неявно и неоправданно предполагается, что между величиной всех изучаемых промеров и уровнем их билатеральной асимметрии сохраняется примерно одинаковая пропорция, которую и выражают нормированные показатели. Однако асимметрия мелко- и крупноразмерных билатеральных органов (признаков), как правило, имеет не только разный порядок различий, но и несходные механизмы возникновения и разную стоимость их проявления. Нередки ситуации, когда варьирование крупного органа на разных сторонах тела (наибольшее по абсолютной величине) при нормировании приобретает невысокие относительные оценки, которые вносят неоправданно малый вклад в интегральный индекс FA. В свою очередь, оценки изменчивости малозначимых мелкоразмерных структур могут обеспечить существенный вклад в относительный индекс. Поэтому при расчетах интегральных показателей следует в большей степени ориентироваться на оценки различий в абсолютном масштабе.

Отдельно стоит рассмотреть вопрос о количественном и качественном составе показателей асимметрии отдельных признаков, объединяемых в интегральные индексы. Обычно в состав индексов входят показатели асимметрии одной категории признаков: или только качественные, или меристические, или пластические (Методические…, 2003, Гелашвили и др., 2004). Однако и в пределах этих групп асимметрия одних признаков может оказывать более существенное влияние на интегральную оценку, чем других. Например, предполагается (Leung, 2000), что при увеличении согласованной изменчивости асимметрий признаков в пределах выборки чувствительность индексов уменьшается. Наличие корреляции между показателями асимметрии разных признаков также может оказывать влияние на повышение вероятности появления ошибок первого рода.

Базовый способ нормировки статистических данных, нормированное отклонение (x – M) / S (используется в показателе fa_ij(4), табл. 4: 4), выступает альтернативой рассмотренных показателей и индексов асимметрии. Эта универсальная величина независимо от исследуемого признака показывает, на каком расстоянии (в единицах стандартного отклонения) находится его конкретное значение от центра распределения. С ее помощью можно сравнивать объекты разного качества (организмы разных видов, пород, возрастов и т. д.) по нескольким свойствам (Ивантер, Коросов, 2003). Процедура сохраняет исходно нормальное распределение признаков (в нашем случае – разницы между лево- и правосторонними промерами, показатель fa_ij(4) на рис. 3: 4), приводит все признаки к одинаковому диапазону изменчивости (примерно ±3) и позволяет выполнять их суммирование с признанием равной информационной значимости. Это дает возможность проводить сравнение выборок с использованием точных параметрических критериев (Зорина, Коросов, 2009; Зорина, 2009).

Процедура нормирования сохраняет нормальное распределение разницы сторон и для индекса FA₄. Чем больше признаков объекта исследования имеет массовые проявления ненаправленной асимметрии, то есть чем шире основания распределения fa_ij(4) для каждого признака, тем больше будет размах колебаний интегрального показателя fa_i(4) и выше значение его дисперсии FA₄ = S²(fa_i(4)). Таким образом, показатель, основанный на нормированном отклонении, учитывает массовые проявления флуктуирующей асимметрии и в меньшей мере зависит от случайностей при формировании выборок.

Иногда при определении величины флуктуирующей асимметрии используют оценки, которые по своей структуре и особенностям расчета существенно отличаются от рассмотренных выше показателей и индексов асимметрии. Например, Трубянов (Трубянов, Глотов, 2010) вводит новый  показатель флуктуирующей асимметрии − показатель «ковариации - корреляции» (CVR), который в явном виде  и в равной степени включает коэффициент  вариации признака  слева  (или  справа)  (CV)  и  коэффициент  корреляции  между значениями признака слева и справа (ρ) (Трубянов, 2010): CVR = CV ∙ (1 - ρ²). Интегральный индекс на основе данного показателя асимметрии имеет следующий вид: CVR_(FA) = CV_(ср) ∙ (1 - r²_(ср)). Средний  коэффициент  вариации (CV_(ср)) оценивается при помощи  медианы  средних  Уолша,  а  средний  коэффициент  корреляции  (r_(ср)) при помощи z-преобразования.  Распределение  данного  показателя  близко  к нормальному.

Автор считает, что информативность показателя CVR  заключается  не  только  в количественном  значении  самого  показателя, но и его компонент. Коэффициент корреляции  показывает  степень  структурной  взаимосвязи  и  целостности организма,  а  коэффициент  вариации  показывает  степень  изменчивости признака, обусловленную  внутренними  или  внешними  по  отношению  к  организму причинами (Трубянов, 2010). 

Следует отметить, что автор не принял во внимание логические основы создания и статистические характеристики тех коэффициентов, которые он использует при построении нового показателя асимметрии. Если новый показатель и учитывает корреляцию, связанную с фактической изменчивостью флуктуирующей асимметрии, то никак не вычленяет ее из общей корреляционной изменчивости признаков. Например, высокая корреляция признаков слева и справа возникает в том случае, когда анализируется выборка объектов разного размера (при высокой точности промеров даже небольшие отличия объектов по размеру будут существенны), что не имеет никакого отношения к флуктуирующей асимметрии. «Загрязнение» нового показателя возможно и другими видами корреляции, связанными с неравномерностью роста частей самого листа (аллометрией), методическими ошибками и т. д. Во-вторых, следует отметить, что коэффициент вариации признаков, используемый в новом показателе асимметрии, зависит, кроме собственно варьирования, еще и от величины признака, что также не учитывается при проведении расчетов. Поэтому, чтобы ввести в широкое использование данный показатель асимметрии, следует изначально пересмотреть теоретические и статистические основы его построения и провести дополнительные исследования на основе большого объема фактического материала.

 

Заключение

Выбор неадекватного метода оценки флуктуирующей асимметрии может привести к неточному установлению закономерностей в изменении величины асимметрии биологических систем. На основании одних и тех же данных разные показатели асимметрии могут давать разные результаты. Арифметические и статистические преобразования исходных данных (включая разные способы их нормирования) определяют чувствительность и работоспособность показателей асимметрии.

Нарушение изначально нормального распределения разности сторон признаков приводит к необходимости использования грубых непараметрических критериев. Показатели с ненормальным распределением повышают значимость редких случайных отклонений и выдают их за существенные (включая методические огрехи). Сам способ нормирования может приводить к отличиям между выборками, которые сложно интерпретировать.

Индексы рассчитываются путем простого объединения показателей асимметрии отдельных признаков и не учитывают различие их статистических характеристик. Как одно из последствий – нарушение нормального распределения (индексы сохраняют недостатки показателей). Объединение признаков с разным уровнем статистических параметров означает, что наибольшую роль в общей средней особи будут играть только те показатели асимметрии, которые имеют наибольшие значения. Рассматриваются и обычные статистические ошибки, например, когда при объединении показателей с асимметричным распределением применяется процедура усреднения вместо вычисления медианы.  

Как альтернатива рассмотренным оценкам асимметрии отмечается показатель и индекс, основанные на нормированном отклонении. Процедура нормирования сохраняет нормальное распределение разницы сторон, и с ее помощью можно сравнивать объекты разного качества.

Библиография

Благодарности

Автор благодарен А. В. Коросову за разностороннюю помощь в работе.