Введение
Перламутровка Clossiana freija (Thünberg 1791) – постгляциальный реликт лесной зоны, внесенный в Красные книги ряда территориальных образований в Европе и за ее пределами (European Red List…, 2010; Кулак, Яковлев, 2018; ООПТ РФ, 2018 и др.). На западе средней тайги вид приурочен к кустарничково-сфагновым болотам, которые выявляются как местообитания островного типа. Поэтому население на ландшафтном уровне, как правило, организовано по типу метапопуляции, состоящей из пространственно разобщенных биотопических группировок особей (локальных популяций, или субпопуляций). Важнейшими чертами такого образования являются отсутствие больших группировок, выявляющихся как полноценные популяции, наличие потоков расселяющихся особей, связывающих группировки в единую сеть, и асинхронность их динамики на разных участках населенной территории (Хански, 2010). Подобная пространственная организованность делает вид чувствительным к изменению структуры ландшафта, – исчезновение и деградация местообитаний, не только тех, которые заняты стабильными группировками, но и субоптимальных с их эфемерным населением, и транзитных, канализирующих расселение, может приводить к локальному вымиранию. Жизнеспособность метапопуляции во многом зависит от величины и колебаний численности в период размножения, поскольку она во многом определяет успех воспроизводства группировок в отдельных местообитаниях и регулирует их взаимодействие посредством изменения интенсивности расселения.
Пространственную организованность населения перламутровки C. freija изучали в заповеднике «Кивач». По результатам анализа размещения и локальных перемещений имаго на исследуемой территории было выделено три локальные популяции (Горбач, Нечепаренко, 2022). Настоящее исследование посвящено оценке их абсолютной численности и изменчивости демографических показателей в течение репродуктивного периода.
Материалы
Материал для настоящего исследования получен в ходе полевых экспериментов с мечеными особями в заповеднике «Кивач» (Республика Карелия, Кондопожский р-н) в 1996 и 2016 гг. Применяли схему Джолли – Себера с многократно повторяющимися отловами бабочек. Особей метили индивидуальными номерами и сразу же освобождали. Метки наносили нетоксичным перманентным маркером (Pilot-SCA) на нижнюю поверхность заднего правого крыла (Горбач, 2013). В 1996 г. группировки вида исследовали на болотах Близкое и Осоковое (рис. 1); в течение лета имаго – с 29 мая по 23 июня провели 21 отлов. В 2016 г. в эксперимент включили все 11 болот, на которых когда-либо встречали вид в 1995–2015 гг; в период с 23 мая по 3 июня каждое из них удалось посетить от 9 до 11 раз. Изучение разброса точек отловов и локальных перемещений имаго показало, что ключевыми элементами исследуемой системы являются три субпопуляции, две из них приурочены к отдельным болотным массивам – Близкому и № 10, а одна занимает два соседних биотопа – болота Касандровое и Чудесное (Горбач, Нечепаренко, 2022). Перекрывание смоделированных областей оседлости (см. рис. 1) указывает на общность населения этих местообитаний и других выделов, где когда-либо встречали бабочек.
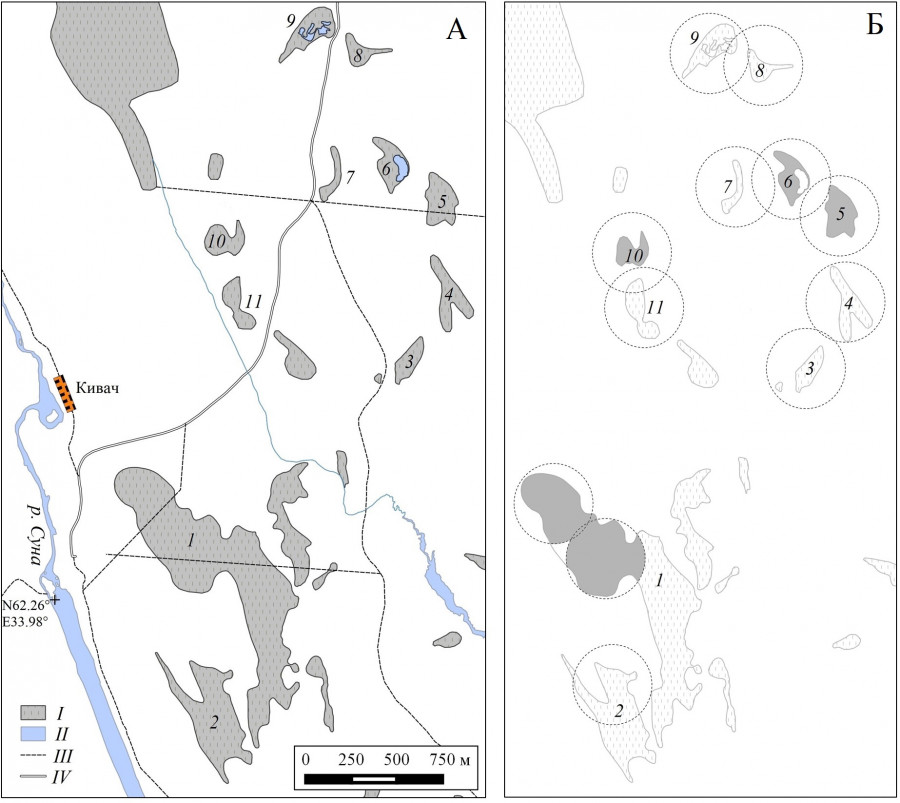
Рис. 1. Территория исследования (А) и пространственная структура популяции Clossiana freija (Б). I – болота, II – водоемы, III – грунтовые дороги, тропы, квартальные просеки и линии ЛЭП, IV – шоссейная дорога Водопад Кивач – Сопоха. Болота, на которых найдены имаго вида: 1 – Близкое (77 га), 2 – Осоковое (22 га), 3 – № 3 (без названия, 3 га), 4 – Голубичное (6 га), 5 – Касандровое (6 га), 6 – Чудесное (4 га), 7 – Придорожное (2 га), 8 – Пограничное (3 га), 9 – Сухая ламба (6 га), 10 – № 10 (4 га), 11 – № 11 (5 га). Окружностями указаны пределы локальных перемещений бабочек на основе оценок их разлета по экспоненциальной модели (по: Горбач, Нечепаренко, 2022), серым цветом выделены местообитания ключевых группировок вида
Fig. 1. The study area (А) and the spatial structure of the Clossiana freija population (Б). I – bogs; II – water bodies; III – dirt roads, trails, quartery grades and power lines; IV – highway from Kivach Waterfall to Sopokha. Sphagnum bogs where butterflies are found: 1 –Blizkoe (77 ha); 2 – Osokovoe (22 ha); 3 – № 3 (3 ha); 4 – Golubichnoe (6 ha); 5 – Kasandrovoe (6 ha); 6 – Chudesnoe (4 ha); 7 – Pridorozhnoe (2 ha); 8 – Pogranichnoe (3 ha); 9 – Sukhaya Lamba (6 ha); 10 – № 10 (4 ha); 11 – № 11 (5 ha). The circles indicate the limits of local movements of butterflies based on the exponential model estimates (according to Gorbach, Necheparenko, 2022), the habitats of local populations of the species are highlighted in gray
Методы
Динамику лета имаго перламутровки C. freija изучали с помощью стохастической модели Джолли – Себера, полагая, что в ходе эксперимента численность локальных популяций увеличивалась за счет бабочек, вышедших из куколок, и иммигрировавших из других мест и уменьшалась вследствие гибели и эмиграции. По частоте повторных отловов получены серии оценок численности и показателей скорости пополнения и элиминации. Полученные значения оптимизировали средствами компьютерной итерации, подгоняя модельные параметры под значение коэффициента ежедневного убывания численности Ø ≤ 1 (Горбач, 2013). Согласованность хода кривых численности проверяли методом Колмогорова – Смирнова (критерий D). Среднюю продолжительность присутствия особи на исследуемой территории определяли согласно выражению Tø = ˗1/lnØ, где Ø – средние и медианные значения коэффициента ежедневного убывания численности в модели Джолли – Себера.
Абсолютную численность локальных популяций и населения всей исследуемой территории оценивали по частоте отловов особей, используя в качестве модели распределение Пуассона. Общая задача состояла в том, чтобы, зная частоты отловов, найти значение нулевого класса, т. е. определить число особей, которые в ходе эксперимента не попались ни разу (Горбач, 2018). Соответствие эмпирических частот теоретической модели устанавливали с помощью критерия Пирсона χ2.
Диапазон варьирования переменных определяли простым непараметрическим бутстрепом (Шитиков, 2012). Доверительные интервалы рассчитывали методом процентилей с числом итераций B = 1000, достаточным для уровня вероятности P = 0.95. Показатели сравнивали с помощью рандомизационного теста (MCR – Monte Carlo Randomization) с тем же числом испытаний B. Значимость отличий p при таком подходе представляет собой скорректированную долю нуль-модельных комбинаций (эмпирическая разность не больше рандомизированной, |Dobs| ≤ |Dran|) от общего числа испытаний B. Критической величиной для p принято стандартное значение α = 0.05. Значимость отклонений от пропорции 1:1 в соотношении полов проверяли критерием Пирсона χ2.
Данные обрабатывали в среде MS Excel и R 4.1.0 (R Core Team, 2020) с использованием базовых функций и функций пакета boot (Canty, Ripley, 2022; Davison, Hinkley, 1997).
Результаты
Период размножения перламутровки C. freija в 1996 г. длился около трех недель. Фаза активного лета пришлась на первую половину июня (рис. 2). Динамика имаго отличалась по половому признаку: самцы начали появляться за 5 дней до первых самок, их численность достигла наибольших значений к моменту массового вылета последних. Во второй половине рассматриваемого периода преобладали самки, они попадались еще около недели после исчезновения самцов. Результаты сравнения временных рядов указывают на значимую дифференциацию хода кривых (критерий Колмогорова – Смирнова: D = 6.18, p < 0.001). Между тем в период массового лета скорость ежедневного убывания численности Ni, измеряемая коэффициентом Ø, и рассчитанное время присутствия особи на исследуемой территории Tø не отличались у особей разных полов ни по одной из статистик (табл. 1, MCR-тест: p > 0.538). Около 65 % имаго не погибали и не эмигрировали по крайней мере в течение суток. Обобщенные показатели скорости пополнения исследованной локальной популяции, выраженной коэффициентом пропорциональности от численности Ni+1, приняли следующие значения: средняя M = 0.35 (0.22 ÷ 0.47), стандартное отклонение S = 0.19 (0.11 ÷ 0.25) и медиана Me = 0.33 (0.13 ÷ 0.62). Время между первым и последним отловом особи варьировало от 1 до 8 дней. Широкие перекрывания доверительных интервалов средних и медианных оценок времени Tø и T указывают на случайность отличий модельных аппроксимаций и экспериментальных данных. Если исходить из максимального биологически адекватного значения коэффициента Øi = 0.92 неоптимизированной модели Джолли – Себера, то особь могла оставаться на исследуемой территории до 12 дней.
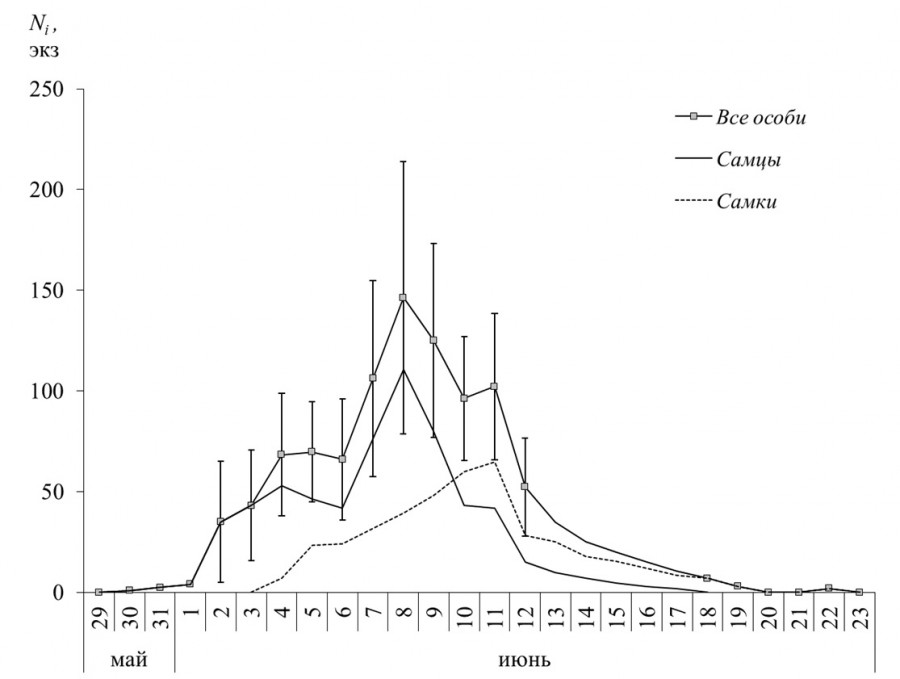
Рис. 2. Динамика лета имаго перламутровки Clossiana freija на болотах Близкое и Осоковое в 1996 г. Ni – численность особей по модели Джолли – Себера, «усами» указана величина стандартной ошибки
Fig. 2. Dynamics of adults flight of Clossiana freija in the Blizkoe and Osokovoe bogs in 1996. Ni is the number of individuals according to the Jolly – Seber model, the value of the standard error is indicated by the “whiskers”
Таблица 1. Коэффициент ежедневного убывания численности и время присутствия имаго Clossiana freija на болотах Близкое и Осоковое в 1996 г.
| Показатель | Самцы | Самки | Все особи | |
| Ø | n | 8 | 6 | 9 |
| xmin | 0.44 | 0.33 | 0.34 | |
| xmax | 0.92 | 1.00 | 1.00 | |
| M | 0.65 (0.54 ÷ 0.77) | 0.70 (0.54 ÷ 0.86) | 0.66 (0.54 ÷ 0.78) | |
| S | 0.18 (0.08 ÷ 0.22) | 0.22 (0.05 ÷ 0.30) | 0.20 (0.09 ÷ 0.26) | |
| Me | 0.64 (0.46 ÷ 0.88) | 0.72 (0.48 ÷ 0.90) | 0.64 (0.46 ÷ 0.84) | |
| Tø | M | 2.3 (1.6 ÷ 3.8) | 2.8 (1.6 ÷ 6.6) | 2.4 (1.6 ÷ 4.0) |
| Me | 2.2 (1.3 ÷ 7.8) | 3.0 (1.4 ÷ 9.5) | 2.2 (1.3 ÷ 5.7) | |
| T | n | 60 | 35 | 95 |
| xmax | 7 | 8 | 8 | |
| M | 2.8 (2.3 ÷ 3.2) | 2.9 (2.2 ÷ 3.6) | 2.8 (2.4 ÷ 3.2) | |
| Me | 2 (2 ÷ 3) | 2 (2 ÷ 3) | 2 (2 ÷ 3) | |
Примечание. Ø – коэффициент ежедневного убывания численности, Tø – время присутствия особи на исследованной территории, рассчитанное по Ø (дни); T – число дней между первым и последним отловом особи, n – объем выборки, xmin и xmax – минимальное и максимальное значения, M – средняя арифметическая, S – стандартное отклонение, Me – медиана, интервалы оценок получены методом бутстрепа с числом итераций B = 1000.
В 2016 г. репродуктивный период начался раньше, прекратился в начале июня из-за ухудшения погоды и больше не возобновлялся (рис. 3). Фаза массового лета длилась около недели, самцы появились на четыре дня раньше самок. Регулярность отловов меченых бабочек оказалась недостаточной для того, чтобы получить адекватные описания хода кривых численности для особей разных полов. Динамику лета всех имаго на исследуемой территории определили флуктуации численности населения болота Близкое (критерий Колмогорова – Смирнова: D = 0.73, p = 0.661). Ход кривых в субпопуляции болота № 10 и субпопуляции болот Касандровое и Чудесное был сходен (D = 1.17, p = 0.129) и значимо отличался от общей динамики (D < 1.99, p < 0.001). Сравнение модельных показателей не выявило ни половых, ни межпопуляционных отличий (табл. 2, MCR-тест: p > 0.149). Интервалы обобщенных оценок, полученные для болота Близкое, перекрываются с таковыми 1996 г., указывая на отсутствие значимой сезонной дифференциации (MCR-тест: p > 0.566). Коэффициент пополнения населения для всей территории в среднем составил 0.31 (0.18 ÷ 0.45) при S = 0.20 (0.09 ÷ 0.25) и Me = 0.29 (0.13 ÷ 0.51). Более выраженная стохастичность модельных параметров, особенно сильно отразившаяся в медианных оценках времени Tø (табл. 3), есть следствие слабой детерминированности встреч особей разного статуса в небольших по объему выборках, – флуктуации доли меченых особей увеличили разброс значений коэффициентов Ø и привели к смещению целого ряда из них в сторону единицы, что интерпретируется как нулевая ежедневная элиминация. Предсказанное время присутствия особи на исследуемой территории в таких случаях равняется 99 дням, значению в несколько раз превышающему максимально возможную продолжительность фазы имаго у данного вида. Вместе с тем модельные аппроксимации на основе средних показателей достаточно хорошо согласуются с результатами наблюдений. Интервал между первым и последним отловом особи достигал 6 дней и в среднем был меньше, чем в 1996 г. (MCR-тест: p < 0.001).
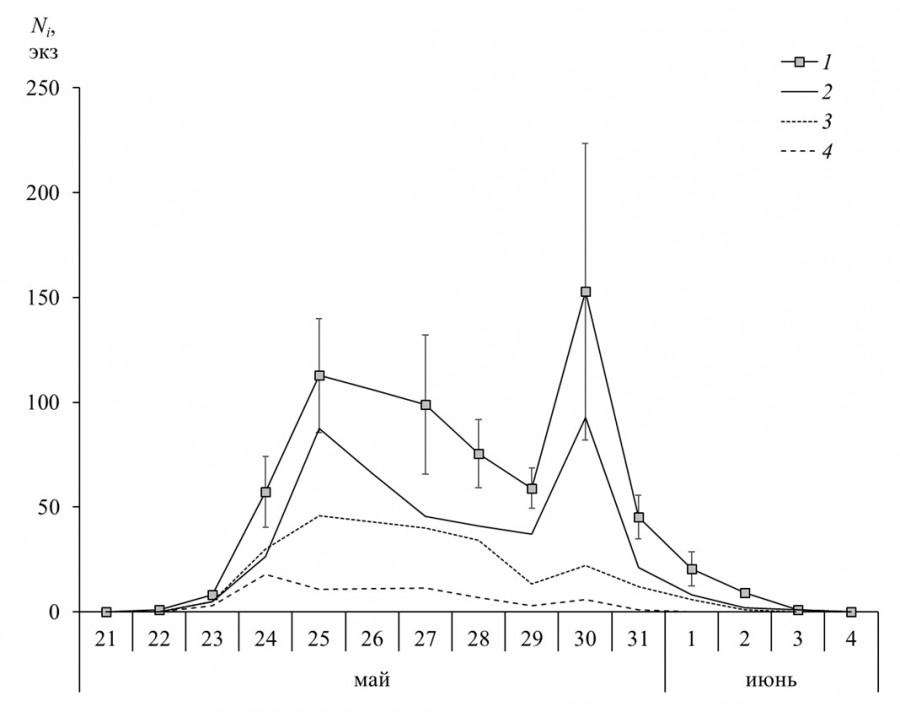
Рис. 3. Динамика лета имаго перламутровки Clossiana freija в 2016 г. Ni – численность особей по модели Джолли – Себера, «усами» указана величина стандартной ошибки, 1 – все группировки на исследуемой территории, 2 – болото Близкое, 3 – болота Касандровое и Чудесное, 4 – болото № 10
Fig. 3. Dynamics of adults flight of Clossiana freija in 2016. 1 – all groups in the study area, 2 – Blizkoye bog, 3 – Kasandrovoe and Chudesnoe bogs, 4 – bog № 10. Ni is the number of individuals according to the Jolly – Seber model, the value of the standard error is indicated by the “whisker”
Таблица 2. Коэффициент ежедневного убывания численности и время присутствия имаго перламутровки Clossiana freija на исследуемой территории в 2016 г.
| Показатель | Локальные популяции | Вся территория | |||
| Близкое | Касандровое и Чудесное | Болото № 10 | |||
| Ø | n | 7 | 6 | 4 | 7 |
| xmin | 0.08 | 0.33 | 0.20 | 0.21 | |
| xmax | 1.00 | 1.00 | 1.00 | 1.00 | |
| M | 0.52 (0.31 ÷ 0.76) | 0.64 (0.44 ÷ 0.85) | 0.69 (0.39 ÷ 0.92) | 0.63 (0.42 ÷ 0.83) | |
| S | 0.34 (0.12 ÷ 0.43) | 0.28 (0.10 ÷ 0.33) | 0.38 (0.01 ÷ 0.46) | 0.30 (0.15 ÷ 0.37) | |
| Me | 0.41 (0.35 ÷ 1.00) | 0.57 (0.38 ÷ 0.97) | 0.78 (0.20 ÷ 1.00) | 0.58 (0.35 ÷ 0.96) | |
| Tø | M | 1.5 (0.9 ÷ 3.6) | 2.2 (1.2 ÷ 6.2) | 2.7 (1.1 ÷ 12) | 2.2 (1.2 ÷ 5.4) |
| Me | 1.1 (1.0 ÷ >15) | 1.8 (1.0 ÷ >15) | 4.0 (0.6 ÷ >15) | 1.8 (1.0 ÷ >15) | |
| T | n | 57 | 30 | 14 | 112 |
| xmax | 5 | 4 | 6 | 6 | |
| M | 1.8 (1.6 ÷ 2.1) | 1.5 (1.2 ÷ 1.8) | 1.9 (1.4 ÷ 2.6) | 1.8 (1.6 ÷ 2.0) | |
| Me | 1 (1 ÷ 2) | 1 (1 ÷ 2) | 2 (1 ÷ 2) | 1 (1 ÷ 2) | |
Примечание. Обозначения даны в табл. 1.
Анализ частот отловов показал соответствие эмпирических распределений закону Пуассона (см. табл. 3). Лишь в 1996 г. отличия были существенными. Выявленные отклонения есть следствие роста доли меченых особей в отловах, что указывает на уменьшение элиминации и, следовательно, не противоречит теоретическим обоснованиям использования распределения Пуассона для оценки абсолютной численности (Горбач, 2018). Численность бабочек на болотах Близкое и Осоковое в 1996 г. была выше, чем на всей исследуемой территории в 2016 г., в обоих случаях преобладали самцы в соотношении 1:1.4 и 1:1.5 (критерий Пирсона: χ2 > 6.61, p < 0.011). Самыми крупными группировками в 2016 г., примерно равными по численности, были локальные популяции на болоте Близкое и болотах Касандровое и Чудесное, но по половому составу они существенно различались. В первом случае соотношение полов 1:1.2 (1 ÷ 1.3) не отличалось от равномерного распределения (χ2 < 1.25, p > 0.264), во втором – самцов было в 3.2 (2.6 ÷ 4) раза больше, чем самок (χ2 > 16.49, p < 0.001). Преобладание самцов в малочисленной субпопуляции болота № 10, в среднем 1:1.6, незначимо (χ2 = 1.19, p = 0.275) из-за чувствительности используемого критерия к величине абсолютных отличий сравниваемых частот.
Таблица 3. Абсолютная численность перламутровки Clossiana freija
| Пол | Частота отлова особи | Nабс., экз. | lim, экз. | χ2 | p | ||||
| 1 | 2 | 3 | 4 | 5 | |||||
| Близкое и Осоковое, 1996 г. (Горбач, 2018) | |||||||||
| Самцы | 61 | 37 | 10 | 1 | 0 | 178 | 159 ÷ 206 | 2.638 | 0.450 |
| Самки | 42 | 29 | 3 | 0 | 0 | 131 | 114 ÷ 157 | 7.123 | 0.028 |
| Все особи | 103 | 66 | 13 | 1 | 0 | 307 | 276 ÷ 338 | 8.445 | 0.037 |
| Близкое, 2016 г. (Горбач, 2018) | |||||||||
| Самцы | 19 | 17 | 7 | 1 | 1 | 60 | 54 ÷ 70 | 1.424 | 0.840 |
| Самки | 18 | 11 | 3 | 1 | 0 | 51 | 43 ÷ 69 | 0.244 | 0.970 |
| Все особи | 37 | 28 | 10 | 2 | 1 | 110 | 100 ÷ 125 | 1.081 | 0.897 |
| Касандровое и Чудесное, 2016 г. | |||||||||
| Самцы | 27 | 8 | 0 | 1 | 0 | 84 | 60 ÷ 136 | 0.270 | 0.874 |
| Самки | 8 | 7 | 4 | 0 | 0 | 26 | 23 ÷ 34 | 0.342 | 0.843 |
| Все особи | 35 | 15 | 4 | 1 | 0 | 97 | 82 ÷ 127 | 0.011 | 0.999 |
| № 10, 2016 г. | |||||||||
| Самцы | 4 | 4 | 1 | 0 | 0 | 13 | 11 ÷ 26 | 0.847 | 0.655 |
| Самки | 2 | 3 | 1 | 1 | 0 | 8 | 8 ÷ 13 | 0.457 | 0.928 |
| Все особи | 6 | 7 | 2 | 1 | 0 | 21 | 19 ÷ 27 | 0.988 | 0.804 |
| Вся исследуемая территория, 2016 г. | |||||||||
| Самцы | 53 | 29 | 8 | 2 | 1 | 146 | 129 ÷ 174 | 0.661 | 0.956 |
| Самки | 34 | 21 | 8 | 2 | 0 | 96 | 86 ÷ 115 | 0.330 | 0.954 |
| Все особи | 87 | 50 | 16 | 4 | 1 | 242 | 221 ÷ 273 | 0.296 | 0.990 |
Примечание. Nабс. – оценка абсолютной численности, lim – интервал оценки, полученный методом бутстрепа с числом итераций B = 1000, χ2 и p – критерий соответствия распределению Пуассона и его значимость.
Обсуждение
Лет имаго перламутровки C. freija на западе европейской тайги обычно начинается в последней декаде мая и длится три-четыре недели (Marttila et al., 2000). Задержка в 1996 г. связана c холодной погодой: майская среднесуточная температура колебалась в диапазоне от 1 до 18 °С, опускаясь ниже 5 °С 18 раз. В 2016 г. этот показатель превышал 6 °С и лишь четверо суток был ниже 10 °С. С наступлением благоприятных условий имаго появлялись синхронно в разных местах и их численность в течение нескольких суток быстро нарастала, достигая максимальных значений. При неустойчивой погоде вылет новых бабочек растягивается во времени и период размножения обычно проходит без ярко выраженных экстремумов. При долговременном ухудшении погодных условий лет имаго прерывается и обычно не возобновляется, как это было в 2016 г. Однако в другие сезоны отдельные бабочки встречались и после подобных кризисов, – здесь многое зависит от глубины и продолжительности похолоданий.
Биологический смысл более раннего вылета самцов заключается в повышении эффективности воспроизводства популяции: к моменту появления самок их концентрация достигает максимальных значений, тем самым обеспечивается конкуренция и возрастает частота спариваний. Результаты моделирования (Zonneveld, 1991) предсказывают рост числа оплодотворенных самок при увеличении доли самцов. Самки перламутровок спариваются один раз (Baguette, Nève, 1994). Поскольку обычно оплодотворение происходит вскоре после выхода самки из куколки, число неоплодотворенных особей большую часть репродуктивного периода сохраняется на относительно низком уровне, считают, что их дефицит способствует расселению самцов, вынуждая их покидать нативные местообитания (Baguette et al., 1998; Petit et al., 2001). Отсутствие существенной половой дифференциации модельных параметров (см. табл. 1) оставляет временной сдвиг единственной значимой причиной отличия динамики лета самцов и самок. Медленный рост численности самок в первой половине репродуктивного периода (см. рис. 2) объясняется их относительно низкой индивидуальной активностью. По выходе из куколок самки реже, чем самцы, обнаруживают себя, только отложив большую часть яиц, они становятся более подвижными, и значит, более заметными и доступными для отлова. К концу репродуктивного периода они начинают активно расселяться, именно в это время меченые особи наиболее часто попадались вдали от местообитаний, где были отловлены впервые.
Сильную стохастичность модельных параметров, такую как показана для локальных популяций в 2016 г., можно уменьшать, ограничив значения коэффициента элиминации при оптимизации модели Джолли – Себера не максимально возможным с биологической точки зрения значением коэффициента ежедневного убывания численности Ø = 1 (Горбач, 2013), а Ø = exp(˗1/Tmax), где Tmax – наибольший диапазон между первым и последним отловом особи в днях. В любом случае, аппроксимации, выполненные на основе малых выборок, вряд ли будут вполне надежными (Горбач, 2018).
Асинхронность хода кривых численности в выделенных локальных популяциях (см. рис. 3) указывает на их автономность. Аналогичные явления обычны в пространственно разобщенных популяциях бабочек (Thomas, Harrison, 1992; Sutcliffe et al., 1996), в том числе и у болотных перламутровок (Schtickzelle et al., 2002; Baguette, Schtickzelle, 2003). Всплеск численности во второй половине репродуктивного периода 2016 г. связан с кумулятивным эффектом роста доли впервые отловленных в исследуемых выделах особей. Среди них преобладали новые, но были и меченые в других местах бабочки. Принимая во внимание тот факт, что почти все они были одинаково облетаны, можно предположить, что значительную часть прироста обеспечили именно расселяющиеся особи, известные и неизвестные по своему происхождению. Сходное явление неоднократно наблюдали и в одной из заонежских популяций мнемозины (Горбач, Кабанен, 2009). Такие возмущения бывают заметны при небольшой численности группировок, когда добавление каждой новой варианты заметно влияет на структуру эмпирических данных. Кроме того, известно, что при росте населения вероятность миграции уменьшается (Konvicka et al., 2012). Выявленные сезонные различия частот повторных отловов и интервалов между первым и последним отловом особи на болоте Близкое поддерживают этот вывод, указывая на то, что бабочки дольше оставались в местообитании при высокой численности. В таких условиях расселение, по-видимому, происходит латентно, без явных демографических всплесков.
Приоритет болота Близкое в обеспечении жизнеспособности рассматриваемой метапопуляции перламутровки C. freija определили наибольшая абсолютная численность населения и вклад в общую динамику лета имаго на исследованной территории. По числу бабочек локальная популяция с болот Касандровое и Чудесное номинально не уступает ей, но выявленная половая диспропорция снижает репродуктивный потенциал последней. Одно из объяснений нарушения полового баланса базируется на рассмотренном выше явлении более раннего вылета самцов (Tabashnik, 1980): при условии равной ежедневной смертности на преимагинальных стадиях преимущество получают те особи, которые быстрее заканчивают развитие, поэтому половозрелых самцов в популяциях всегда больше, чем самок. Развивая эту мысль, мы выдвинули гипотезу, что посредством изменения в соотношении полов возможна регуляция численности (Горбач, 1998). В условиях высокой преимагинальной смертности доля самцов возрастает, это увеличивает число оплодотворенных самок и, следовательно, численность потомства. Низкая смертность ведет к паритету, число неоплодотворенных самок увеличивается, замедляя рост популяции. Такая точка зрения поддерживается моделированием систем спаривания (Zonneveld, 1991), результаты которого предсказывают низкую вероятность оплодотворения всех самок при равном соотношении полов, но разница в скорости развития, составляющая несколько дней, не может объяснить наблюдаемых диспропорций. С интерпретацией результатов полевых экспериментов также возникают проблемы, поскольку исходное состояние исследуемых локальных популяций, как правило, неизвестно. Рост численности должен уменьшать половой дисбаланс, но если, например, репродуктивный период оказывается неудачным и отложено небольшое число оплодотворенных яиц, то и численность имаго на следующий год будет невысокой даже при низкой преимагинальной смертности особей, и наоборот. Еще больше усложняет ситуацию расселение: миграционные потоки между пространственно разобщенными группировками способны непредсказуемым образом изменять соотношение полов. Полностью контролировать его динамику не представляется возможным, поскольку нет способов идентификации иммигрантов среди впервые отловленных особей.
Численность и динамика лета имаго играют важную роль в формировании потоков расселяющихся особей, которые обеспечивают взаимодействие пространственно обособленных группировок и колонизацию новых и освободившихся местообитаний. Локальные популяции на пике численности дают больше мигрантов, вероятность проникновения в другие местообитания при этом возрастает. Уменьшение населения на оптимальных для вида участках ведет к исчезновению небольших группировок и общему сокращению встречаемости на ландшафтном уровне. По результатам двух экспериментов сложно судить о направленности демографических процессов в исследуемой популяции. Перламутровка C. freija в заповеднике «Кивач» не бывает многочисленной, в 1996 г. наблюдали один из локальных максимумов за последние двадцать лет. Бабочки, помимо изученного выдела, регулярно и в достаточно большом числе попадались на болотах Касандровое, Чудесное и № 10 и спорадически на всех других болотах исследуемой территории. В 2016 г. встречаемость можно определить как обычную.
Негативное изменение в состоянии популяций вида наиболее выражено на южной периферии ареала (Кулак, Яковлев, 2018), но и на Европейском Севере имеет место сходная тенденция: результаты мониторинга показывают, что число встреч вида в Финляндии в нынешнем столетии существенно сократилось (Saarinen, Jantunen, 2013). Это явление, охватившее в той или иной мере всех северных по происхождению бабочек, объясняют изменением климатических условий и связывают с глобальным потеплением (Hekkinen et al., 2010). Увеличение инсоляции в летний период ведет к разогреву поверхности мохового покрова, делая условия менее благоприятными для развития. Виды, в том числе и перламутровка C. freija, ранние личиночные стадии которых приходятся на середину лета, по-видимому, наиболее сильно страдают от флуктуаций микроклиматического режима, – маленькие гусеницы в силу ограниченной подвижности не способны быстро перемещаться в затененные места при неблагоприятном развитии ситуации.
Заключение
Таким образом, пространственную организованность популяции перламутровки B. freija можно определить как устойчивую: за прошедшее между исследованиями десятилетие ее конфигурация существенно не изменилась. Численность представляется приемлемой для поддержания воспроизводства и обеспечения связности локальных популяций. Ландшафт с транзитными коридорами и субоптимальными местообитаниями способствует активному расселению, а подвижность бабочек позволяет повторно колонизировать любое из местообитаний на исследуемой территории в случае локального вымирания вида. Интенсивность потоков особей между тем не велика, что, по-видимому, способствует автономности локальных популяций. В условиях заповедного режима причиной деградации сложившейся популяционной системы может стать устойчивое падение качества местообитаний из-за связанных с глобальным потеплением изменений погоды.
Библиография
Горбач В. В. Сезонная динамика численности и половой состав популяции перламутровки Boloria aquilonaris (Lepidoptera, Nymphalidae) // Зоологический журнал. 1998. Т. 77, № 5. С. 576–581.
Горбач В. В. Изучение динамики численности методом Джолли – Себера на примере имаго булавоусых чешуекрылых (Insecta, Lepidoptera: Hesprioidea et Papilionoidea) // Принципы экологии. 2013.№2. С. 14–28. DOI: 10.15393/j1.art.2013.2601
Горбач В. В. Опыт оценки абсолютной численности популяции по распределению числа отловов в эксперименте с мечением на примере имаго перламутровок рода Boloria (Insecta, Lepidoptera, Nymphalidae) // Принципы экологии. 2018. № 3. С. 24–33. DOI: 10.15393/j1.art.2018.7763
Горбач В. В., Нечепаренко Н. А. Размещение и расселение имаго в популяции перламутровки Clossiana freija (Insecta, Lepidoptera, Nymphalidae) в среднетаежном ландшафте // Энтомологическое обозрение. 2022. Т. 101, № 3. С. 515–532. DOI: 10.31857/S0367144522030030
Горбач В. В., Кабанен Д. Н. Пространственная организованность популяции черного аполлона (Parnassius mnemosyne) в условиях Заонежья // Зоологический журнал. 2009. Т. 88, № 12. С. 1493–1505.
Кулак А. В., Яковлев Р. В. Созологический анализ дневных чешуекрылых (Lepidoptera, Papilionoidea) верховых болот Беларуси // Ukrainian Journal of Ecology. 2018. Vol. 8, № 1. P. 174–193. DOI: 10.15421/2017_203
ООПТ РФ. Информационно-аналитическая система «Особо охраняемые природные территории России»: Boloria freija (Becklin in Thunberg, 1791) . URL: http://oopt.aari.ru/bio/57419/ (дата обращения: 28.01.2023).
Хански И. Ускользающий мир: экологические последствия утраты местообитаний . М.: Товарищество научных изданий КМК, 2010. 340 с.
Шитиков В. К. Использование рандомизации и бутстрепа при обработке результатов экологических наблюдений // Принципы экологии. 2012. № 1. С. 4–24.
Baguette M., Schtickzelle N. Local population dynamics are important to the conservation of metapopulations in highly fragmented landscapes // Journal of Animal Ecology. 2003. Vol. 40, № 2. P. 404–412. DOI: 10.1046/j.1365-2664.2003.00791.x
Baguette M., Nève G. Adult movements between populations in the specialist butterfly Proclossiana eunomia (Lepidoptera, Nymphalidae) // Ecological Entomology. 1994. Vol. 19, № 1. P. 1–15.
Baguette M., Vansteenwegen C., Convie I., Nève G. Sex-biased density-dependent migration in a metapopulation of the butterfly Proclossiana eunomia // Acta Oecologica. 1998. Vol. 19, № 1. P. 17–24.
Canty A., Ripley B. D. Package 'boot': Bootstrap Functions (Originally by Angelo Canty for S). R package version 1.3-28.1 URL: https://cran.r-project.org/web/packages/boot/boot.pdf (дата обращения: 23.02.2022).
Davison A. C., Hinkley D. V. Bootstrap Methods and Their Applications. Cambridge: Cambridge University Press, 1997. 582 p. URL: http://statwww.epfl.ch/davison/BMA/ (дата обращения: 23.08.2021).
European Red List of Butterflies. Luxemburg: Publication Office of the European Union, 2010. 48 p. URL: https://ec.europa.eu/environment/nature/conservation/species/redlist/downloads/European_butterflies.pdf (дата обращения: 28.01.2023).
Heikkinen R. K., Luoto M., Leikola N., Pöyry J., Settele J., Kudrna O., Marmion M., Fronzek S., Thuiller W. Assessing the vulnerability of European butterflies to climate change using multiple criteria // Biodiversity and Conservation. 2010. Vol. 19, № 3. P. 695–723. DOI: 10.1007/s10531-009-9728-x
Konvicka M., Zimmermann K., Klimova M., Hula V., Fric Z. Inverse link between density and dispersal distance in butterflies: field evidence from six co-occurring species // Population Ecology. 2012. Vol. 54, № 1. P. 91–101. DOI: 10.1007/s10144-011-0277-2
Marttila O., Saarinen K., Aarnio H., Haahtela T., Ojalainen P. Päiväperhosopas. Suomi ja lähialueet. Helsinki: Tammi, 2000. 231 s.
Petit S., Moilanen A., Hanski I., Baguette M. Metapopulation dynamics of the bog fritillary butterfly: movements between habitat patches // Oikos. 2001. Vol. 92, № 3. P. 491–500.
R Core Team. R: a language and environment for statistical computing. R version 4.0.1. Vienna: R Foundation for Statistical Computing, 2020. URL: http://www.r-project.org/ (дата обращения: 2020-06-06).
Saarinen K., Jantunen J. Paivaperhoset matkalla pohjoiseen. Tuloksia paivaperhosseuranta 1991–2012 ja ennustuksia tulevasta. Helsinki: Tibiale, 2013. 248 p.
Schtickzelle N., Le Boulenge E., Baguette M. Metapopulation dynamics of the bog fritillary butterfly: demographic processes in a patchy population // Oikos. 2002. Vol. 97, № 3. P. 349–360. DOI: 10.1034/j.1600-0706.2002.970305.x
Sutcliffe O. L., Thomas C. D., Moss D. Spatial synchrony and asynchrony in butterfly population dynamics // Journal of Animal Ecology. 1996. Vol. 65, № 1. P. 85–95.
Tabashnik B. Population structure of pierid butterflies. III. Pest populations of Colias philodice eriphyle // Oecologia. 1980. Vol. 47, № 2. P. 175–183.
Thomas C. D., Harrison S. Spatial dynamics of patchily distributed butterfly species // Journal of Animal Ecology. 1992. Vol. 61, № 2. P. 437–446.
Zonneveld C. Models on butterfly protandry: virgin females are at risk to die // Theoretical Population Biology. 1991. Vol. 40, № 3. P. 308–321.
Благодарности
Мы признательны О. В. Фоминой и Н. Н. Кутенковой за гостеприимство и помощь в организации исследований в заповеднике «Кивач».






 © 2011 - 2026
© 2011 - 2026