Введение
Для описания динамики численности животных широко используются усредненные по годам показатели (численности популяции, доли разновозрастных животных и др.). При этом значения популяционных показателей, полученные в разные годы, выступают в роли выборки независимых вариант. Фактически же разные состояния популяции в смежные годы (выраженные демографическими показателями), связаны причинно-следственными связями, информация о которых, однако, при простом статистическом обобщении остается невыясненной. Статистические оценки популяционных свойств могут создать противоречивый образ популяции, не способной к существованию с такими параметрами. Исследование преемственности изменений состояния популяции доступно практи-чески только динамическому моделированию ‒ даже в простой форме имитационной мо-дели (Коросов, 2002). В отличие от статистических параметров модельные (динамические) параметры характеризуют не видимую данность, но структуру взаимоотношений пере-менных. Параметры адекватной динамической модели «по условию» согласованы друг с другом и могут непротиворечиво описывать феномен популяционной динамики. Положим целью дальнейшего изложения построение динамической имитационной модели, которая должна реализовать усредненное описание динамики популяции.Традиционные методы исследований
В качестве объекта моделирования возьмем популяцию темной полевки, детально изученную в Карелии (Ивантер, 1975; Ивантер Э. В., Ивантер Т. В., 1986). Все характеристики получены путем непосредственного подсчета числа животных того или иного статуса среди отловленных в ловушки с последующим расчетом их соотношений в общем объеме выборки.
Темная полевка – вид-эфемер. Перезимовавшие особи весной созревают и приступают к размножению, новорожденные быстро растут и наряду с зимовавшими принимают участие в размножении. К осени зимовавшие успевают дать по 3–5 выводков, а сеголетки — по 1–3 выводка. Плодовитость в среднем по всем группам составляет 5.69 экз./самку. Особи, рожденные в конце лета и осенью, не растут, не созревают и остаются зимовать до следующей весны (Ивантер, 1975, с. 172-189). В течение сезона численность популяции (N) в среднем возрастает с 0.05 до 0.35 экз./100 давилко-суток (наблюдения за 36 лет; Ивантер, 1975, с. 189, рис. 57). От весны к осени доля зимовавших (Pad) постепенно падает (от 1 до 0.01), доля созревающих сеголетков (Aj) и общая доля половозрелых животных всех возрастов (Pa) сначала растут, потом падают (наблюдения за 26 лет; Ивантер Э. В., Ивантер Т. В., 1986, с. 72, 74, табл. 6, 9). Все значения получены пересчетом таблицы 5 первоисточника (табл. 1).
Таблица 1. Средние значения параметров динамики популяции темной полевки
| N | Рad | Рa | Aj | |
| май | 0.05 | 1 | 1 | 0 |
| июнь | 0.09 | 0.33 | 0.66 | 0.46 |
| июль | 0.25 | 0.18 | 0.73 | 0.68 |
| август | 0.3 | 0.08 | 0.55 | 0.48 |
| сентябрь | 0.35 | 0.01 | 0.12 | 0.35 |
Оригинальные методы исследований
Модель имитирует цикл воспроизводства популяции с весны до осени. Взрослые самки могут повторно рожать уже через 22 дня, у прибылых самок с момента их зачатия до первых родов проходит минимум 40 дней. В среднем репродуктивный цикл особи приближается к одному месяцу (Ивантер, 1975), поэтому временной шаг модели принят за 1 месяц. В состав модели входит большое число переменных, между которыми установлены следующие взаимоотношения (табл. 2). На каждом шаге модели зимовавшие особи (численностью Nad) входят в состав половозрелых (Na), доля выживших в течение этого месяца составляет Sa. Новорожденные (Nn) выживают лишь частично (Sn), оставшиеся (Nns) пополняют группу сеголетков (Nji). Кроме них в эту группу входят все молодые особи, выжившие на предыдущем шаге (Nji–1). Какая-то доля особей из этой смешанной ювенальной группы выживает (Njs, Sj). Среди прибылых есть половозрелые (Njai), их число рассчитывается как доля (Aj) от выживших прибылых (Njs). Вместе с зимовавшими взрослые прибылые особи образуют группу взрослых (Na). Все половозрелые животные размножаются (плодовитость E). Зимовавшие и прибылые в сумме и образуют популяцию (численностью N'). В модели рассчитаны и относительные объемы групп: доля в популяции зимовавших особей (Pad') и доля в популяции половозрелых особей (зимовавших и сеголетков совместно) (Pa').
Таблица 2. Уравнения динамической модели (на примере июля, строка 7 в табл. 3)
| Описание процесса | Алгебраическое уравнение | Формула Excel |
| Выживание части зимовавших | Nadi = Nadi-1 · Sa | F7=F6*F$2 |
| Появление новорожденных | Nni = Nai-1 · E | G7=L6*E$2 |
| Выживание части новорожденных | Nnsi = Nni · Sn | H7=G7*G$2 |
| Новорожденные пополняют группу прибылых | Nji = Nnsi + Njsi–1 | I7=H7+J6 |
| Выживание части прибылых | Njsi = Nji · Sj | J7=I7*H$2 |
| Созревание прибылых | Njai = Njsi · Aji | K7=J7*E7 |
| Расчет числа всех взрослых | Nai = Nadi + Njai | L7=F7+K7 |
| Расчет общей численности | Ni = Nadi + Nji | M7=F7+I7 |
| Расчет доли зимовавших | Padi = Nadi / Ni | N7 = F7/M7 |
| Расчет доли взрослых | Pai = Nai / Ni | O7 = L7/M7 |
В число модельных переменных входят оценки численности 8 групп (Nad, Nn, Nns, Nj, Njs, Nja, Na, N') и относительные объемы двух групп (Pad', Pa'). Среди них только три явных переменных – N', Pad', Pa', которые сравниваются со своими аналогами в блоке эмпирических данных. Все остальные переменные (Nad, Nn, Nns, Nj, Njs, Nja, Na) – скрытые. Большая дробность представления модели введена для большей прозрачности расчетов. Общая архитектура модели отображена в табл. 2 (настройка модели уже проведена).
В число параметров модели входят следующие величины:
– доля созревающих особей для каждого месяца (Aji);
– плодовитость (E); поскольку в модели учтены особи обоих полов, в расчетах использовали значение Е = 5.69 / 2 = 2.85 (число молодых на пару родителей);
– выживаемость для 3 групп (Sa, Sn, Sj), три этих значения подбирались в процессе настройки модели.
Основой для настройки модели послужили эмпирические данные по сезонной динамике трех популяционных характеристик (N, Pad, Pa), усредненные за много лет (табл. 1, блок B4:E9 в табл. 3). Комплиментарные им значения модельных переменных N', Рad', Рa' вычисляются в модели в блоке M4:O9. Для оценки различий между моделью и реальностью (в качестве функции невязки) выступали суммы квадратов разности между исходными (N, Рad, Рa) и модельными (N', Рad', Рa') переменными (блок P4:R10). Поскольку настройка модели идет по трем переменным одновременно, в качестве весов для каждого из трех отдельных значений функции невязки были взяты обратные значения средних арифметических (блок B10:D10). Общая функция невязки есть сумма произведений частных функций невязки на свои весовые коэффициенты (ячейка S11). Настройка модели выполнялась с помощью встроенного в Excel макроса «Поиск решения» (см.: Коросов, 2002).
Таблица 3. Имитационная система динамической модели воспроизводства популяции темной полевки
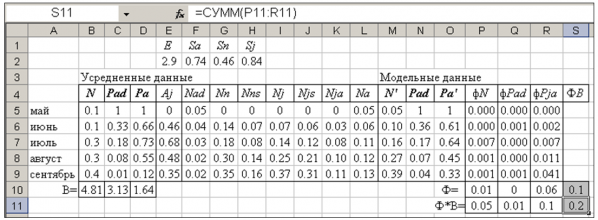
Настройка модели дает однозначное решение при любых стартовых значениях параметров (от 0.01 до 1, хотя иногда требует двукратный запуск макроса): коэффициенты выживаемости составляют для взрослых Sa = 0.74, для новорожденных Sn = 0.46, для сеголетков в целом Sj = 0.84.
При этих параметрах динамика модельных переменных в общих чертах соответствует эмпирическим усредненным данным (табл. 3). Например, снижение доли зимовавших (Pad) модель описывает практически идентично с реальностью (1, 0.36, 0.17, 0.07, 0.04 и 1, 0.33, 0.18, 0.08, 0.01). Модель статистически адекватна исходным данным, тем не менее полного совпадения статистических и модельных описаний нет! Как видно на иллюстрациях, динамика усредненной численности (N) и доли половозрелых особей (Pa) существенно отличается от модельных значений (табл. 2, рис. 1, 2).
При анализе отличий динамики численности полевок, прежде всего, бросается в глаза «горб» значений, приходящийся на июль натурные оценки (N = 0.25) существенно превышают модельные (N' = 0.16 экз./100 ловушко- суток). То же можно сказать и для доли взрослых особей: в июле и августе их в среднем больше (Pa), чем выходит по модели (Pa').
Модель не может воспроизвести средние многолетние характеристики популяции.
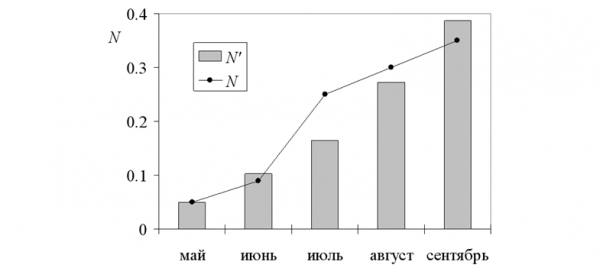
Рис. 1. Динамика численности темной полевки (N, экз./100 ловушко- суток)(%)
Fig. 1. The population dynamics of dark voles (N, ind./100 trap-nights)
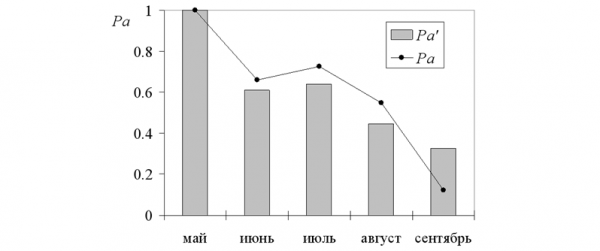
Рис. 2. Доля половозрелых прибылых
Fig. 2. The shares of mature individuals among young
Обсуждение
Почему модель, даже опираясь на эмпирические основания (переменные N, Aj, E), не может воспроизвести средние показатели динамики? Модельные переменные связаны однозначными зависимостями, взаимно детерминированы и не могут быть иными. Жесткость модельных конструкций заставляет искать существо указанных различий в свойствах усредненных демографических характеристик.
Как обобщение многолетних данных, эти значения в высшей степени устойчивы, и добавление новых материалов практически не смещает средние. С другой стороны, усреднялись данные, характеризующие разные уровни численности, фазы динамики и темпы воспроизводства популяции (Ивантер, 1975). В годы пика численности (7 из 36 лет наблюдений) размножение животных начиналось раньше, и максимум численности приходился на июль – август (N, рис. 1). В годы с низким обилием зверьков (29 из 36) максимум достигался лишь к октябрю (рост численности был близок к экспоненте). Взвешенная усредненная кривая столь разных динамических рядов летом образуется сглаженный «горб» (не так ярко выраженный, как при пике). При этом средний уровень численности оказывается существенно ниже, чем на пике, но много более высоким, чем во время депрессии. То же можно сказать и о доле половозрелых особей (Pa, рис. 2). В годы пика численности она велика весной и в начале лета, а во второй его половине и осенью резко снижается (за счет вымирания зимовавших и прохолостания сеголетков). В годы с низкой численностью, напротив, доля взрослых приближается к 100% даже осенью, когда размножение еще не закончилось. Усреднение сглаживает отличия между кривыми динамики и к отчетливому «горбу» в середине лета добавляет лишь очень слабо выраженный «хвост» в сентябре.
Усредненные статистические характеристики, с одной стороны, навязывают модели довольно большой объем размножающихся животных (через Aj и Pa), а с другой – довольно низкие (и неравномерные!) темпы нарастания численности (через N). Однако оказалось, что модельная популяция со средней многолетней динамикой возрастного состава не может поддерживать среднюю многолетнюю динамику численности. Моделирование выявляет внутреннее противоречие усредненных характеристик популяционной динамики: репрезентативное усредненное описание динамики популяции оказывается не вполне адекватным; популяция не живет «в среднем».
Модель можно критиковать как грубое построение, не учитывающее все генерации прибылых. Однако при увеличении дробности ситуация не поменялась бы: какие бы из генераций ни доминировали, но при данном (среднем) уровне численности мы все равно имеет данный (средний) объем половозрелых животных, которые не могут воспроизвести данный (средний) уровень численности, а могут только – иной (более низкий летом и более высокий осенью).
Можно критиковать модель и за то, что она основывается на неких расчетных (умозрительных) величинах выживаемости животных (Sa, Sn, Sj), которые практически невозможно верифицировать, оценить в природе: «что вложишь в модель, то и получишь на выходе».
На наш взгляд, напротив, в возможности оценивать «невидимые» популяционные параметры заключается главная сила моделирования. При поверхностном статистическом описании исследователь может высказывать любые гипотезы о причинах, определяющих тот или иной характер динамики численности. Например, можно предполагать, что выживаемость животных разного возраста одинакова, или не одинакова, или может меняться в течение изучаемого сезона. Эти умозаключения в равной мере проникновенны и безответственны, поскольку простая статистическая обработка не позволяет их проверить.
Моделирование же вводит эти величины в круг предметно обсуждаемых параметров популяции, которые выражают закономерные соотношения наблюдаемых феноменологических характеристик и предопределяют ход популяционной динамики. В частности, модель показала, что выживаемость ниже всего у новорожденных, высока у взрослых сеголетков, а у зимовавших имеет промежуточное значение (Sa = 45%, Sj = 84%, Sa = 74%; табл. 3, блок F1:H2). Полученные цифры пока недостаточны для каких либо существенных заключений (учитывая их безусловное отличие на разных фазах популяционной динамики). Тем не менее модель указала на конкретные противоречия статистической информации о популяции.
Наиболее же существенно, что только опыт моделирования позволил поставить вопрос, о том, сколько фаз динамики численности необходимо описать (пусть и статистически), чтобы составить общее, полное, но непротиворечивое описание динамики популяции? Достаточно ли для темной полевки (учитывая ее в целом невысокую численность) описать динамику только для двух качественно различных состояний – «в годы высокой численности» и «в годы низкой», или же динамика сложной популяционной системы вообще не поддается усреднению без потери адекватности?
Заключение или выводы
Усредненные характеристики хода популяционной динамики содержат большой объем невыявленной информации о функционировании биосистемы. Моделирование позволяет извлечь дополнительную информацию из популяционных статистических характеристик в форме коэффициентов пропорциональности между ними.
Усредненные популяционные характеристики могут противоречить друг другу, создавая ложный образ популяции, которая фактически не способна к существованию с такими параметрами. Популяция не живет «в среднем».
Имитационные динамические модели даже в простой алгебраической форме позволяют выяснить причинно-следственные отношения между ключевыми показателями популяционной динамики и наметить направления дальнейших исследований популяционной динамики.
Библиография
Ивантер Э. В. Популяционная экология мелких млекопитающих таежного Северо-Запада СССР. Л.: Наука, 1975. 246 с.
Ивантер Э. В., Ивантер Т. В. К экологии темной полевки (Microtus agrestis L.) // Экология наземных позвоночных Северо-Запада СССР. Петрозаводск, 1986. С. 64–91.
Коросов А. В. Имитационное моделирование в среде MS Excel (на примерах из экологии). Петрозаводск, 2002. 212 с.
Коросов А. В. Экология обыкновенной гадюк (Vipera berus L.) на Севере (факты и моде-ли). Петрозаводк: Изд-во ПетрГУ, 2010. 264 с.
Благодарности
Работа выполнена при финансовой поддержке Института “Открытое общество. Фонд содействия” (Фонд Сороса – Россия).






 © 2011 - 2026
© 2011 - 2026