Горбач В. В., Сааринен К. Оценка встречаемости и относительного обилия видов в фаунистических исследованиях на примере дневных бабочек Финляндии (Lepidoptera: Hesperioidea, Papilionoidea) // Принципы экологии. 2012. № 2. С. 45–53. DOI: 10.15393/j1.art.2012.1087

Выпуск № 2

Методы экологических исследований

pdf-версия статьи

595.789:574.1:57.087.1

Оценка встречаемости и относительного обилия видов в фаунистических исследованиях на примере дневных бабочек Финляндии (Lepidoptera: Hesperioidea, Papilionoidea)

Введение

Под встречаемостью обычно понимают долю проб от их общего числа, в которых присутствует вид, под относительным обилием – долю особей вида в выборке. Эти показатели призваны дифференцировать виды по их распространенности и численности. В фаунистических работах используют относительное обилие в форме балльных оценок, основанных на субъективных представлениях о статусе того или иного вида – очень редкий, редкий, обычный вид и т. д. Встречаемость описывают, например, как спорадично, локально или широко распространенный вид. Поскольку изучаемые выделы обычно не сопоставимы по величине и интенсивности обследования, а имеющиеся коллекции не отвечают требованию пропорциональности сборов, то структурировать их с использованием количественных мер некорректно. Для данных, собранных по унифицированным методикам, количественные шкалы применимы (Палий, 1965; Зайцев, 1974; Песенко, 1982 и др.), но такие выборки, как правило, невелики: исследования проводят на относительно небольших территориях в течение одного или нескольких сезонов. Реализация национальных программ мониторинга отдельных групп организмов, в частности дневных бабочек (IBMS; NAFI; UKBMS и др.), во многом снимает ограничения подобного рода. Целю данной работы является поиск оптимального способа оценки распространенности и численности организмов.

Традиционные методы исследований

Основу предлагаемого метода составляют два апробированных подхода.

1). Использование 10-балльных шкал для описания встречаемости и обилия видов,  в том числе и дневных бабочек (Marttila et al., 1991). Материалом служат коллекции и наблюдения. Принадлежность объектов к классам определяют с помощью словесных характеристик. Положительными сторонами данного подхода является двурядная система оценки статуса видов (встречаемость / обилие) и число градаций, оптимальное для структурирования многовидового населения обширных территориальных выделов. Основной недостаток кроется в отсутствии ясных критериев для определения ширины большинства классовых интервалов.

 2). Оценка относительного обилия видов по 5-балльной, ограниченной сверху логарифмической шкале (Песенко, 1982). В этом случае используют количественные показатели, полученные в результате учетов, отбора проб и т. д. Величина классового интервала такой шкалы имеет последовательно увеличивающуюся длину шага, рассчитываемую по правилу геометрической прогрессии со знаменателем d = N ^{1 / k}, где N – объем выборки, k – число классов. Значение верхней границы a-го класса определяется как N ^{a / k}, где a = 1, 2 …, k. Величина a-го классового интервала вычисляется по формуле b_a = N ^{a / k} – N ^{(a - 1) / k}. Балл, характеризующий объект с n числом наблюдений в выборке объемом N, является целым числом и заключен в промежутке k log_N n ≤ a ≥ (k log_N n + 1). Преимущество данного подхода заключается в наличии формальных критериев для дифференциации видов. Основным ограничением является невозможность получить выборки, адекватно описывающие население обширных территорий.

Оригинальные методы исследований

Реализуемые в ряде стран программы мониторинга позволяют получать необходимую количественную информацию из множества географических точек. Соответственно, появляется возможность изучать структуру населения животных обширной территории, используя логарифмические шкалы (Песенко, 1982). Мы предлагаем применять 10-балльные шкалы и оценивать с их помощью не только обилие, но и встречаемость видов. При этом следует иметь в виду, что имеющиеся базы данных содержат разного рода погрешности. В программах мониторинга участвует множество сменяющих друг друга коллекторов, которые имеют разную  квалификацию и не всегда строго придерживаются стандартной методики. Сюда же добавляется неравномерность в размещении учетных площадок и различная периодичность их использования. 

По этим причинам смещения оценок встречаемости неизбежны. Например, информации по густонаселенным районам относительно больше, чем по малонаселенным, крупные бабочки относительно чаще попадают в выборку, чем малозаметные, редкие виды привлекают больше внимания, чем обычные и т. д. Увеличение объемов выборок снижает величину ошибок репрезентативности, но не снимает проблемы полностью. Однако стохастичность в балльных оценках встречаемости и обилия вида может проявляться даже при небольших изменениях объема выборок. Уменьшить изменчивость можно, подгоняя  размер полученных после шкалирования частотных классов под некие заданные распределения частот. Такие распределения должны иметь более стабильную структуру по сравнению с наблюдаемыми частотами и в идеале представлять одну из известных теоретических моделей (например, равномерное или нормальное). Основной критерий отбора – отсутствие значимых отличий эмпирического распределения от теоретического.

Алгоритм подгонки эмпирического распределения под теоретическое состоял в следующем. По результатам натурного исследования совокупность видов дифференцировали по встречаемости и обилию, используя 10-бальную шкалу. Далее состав групп видов корректировали за счет изменения групповой принадлежности видов, имеющих оценки обилия, близкие к границам классовых интервалов. Например, если первый класс  эмпирического распределения (группа видов) включал большее число вариант (видов), чем должно быть исходя из подобранного распределения, то лишние варианты (виды, имеющие максимальные для данной группы значения исходных показателей) добавляли во второй класс. Если в итоге во втором классе оказывалось меньше видов, чем следует из теоретической модели, то сюда перемещали виды с самой низкой встречаемостью (или обилием) из третьего класса и т. д. Манипуляции проводили до тех пор, пока отличия между эмпирическими и подобранными частотами не обнулялись. В результате удается получить более адекватное описание генеральной совокупности, общей структуры биоразнооразия изучаемой группы. 

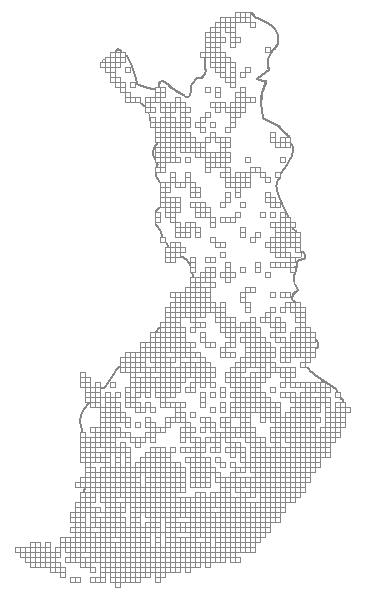
В качестве примера взяли результаты учетов дневных бабочек в Финляндии (Marttila et al., 1999; Saarinen et al., 2003). Бабочек учитывали на маршрутах в квадратах 10×10 км в 1991–2011 годах (рис. 1). Использовали метод трансект Полларда, модифицированный для целей мониторинга (Pollard, Yates, 1993). Общее число обследованных квадратов – 2092, число зарегистрированных бабочек – 4325249 (NAFI). Варианты шкал представлены в табл. 1 и 2.

Встречаемость и относительное обилие оценено для всех бабочек, известных с территории Финляндии к настоящему времени (табл. 3).

Рис. 1. Сеть квадратов 10×10 км, в которых проводили учеты в 1991–2011 гг. по программе мониторинга бабочек Финляндии (NAFI)

Fig. 1. 10×10 km grid squares in which the butterflies were counted over 1991–2011

 

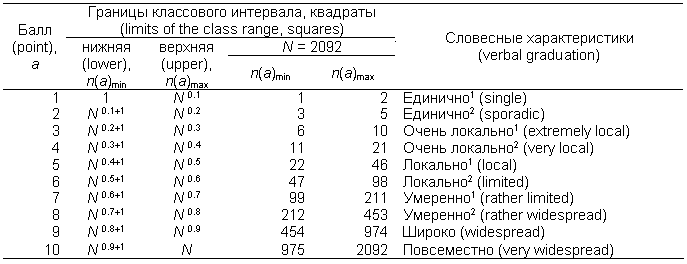
Таблица 1. 10-балльная шкала для оценки встречаемости видов

Table 1. 10-point scale for measurement of the species occurrence

* – число квадратов (10×10 км), в которых вид был встречен хотя бы один раз

 

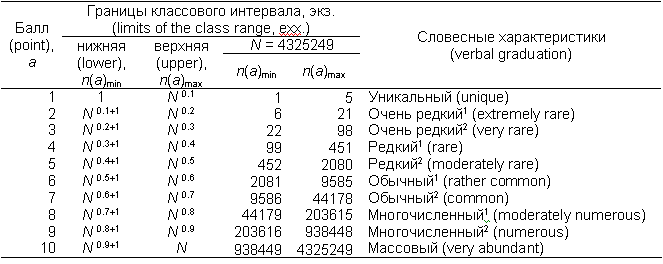
Таблица 2. 10-балльная шкала для оценки относительного обилия видов

Table 2. 10-point scale for measurement of the species relative abundance

* – общее число зарегистрированных особей вида

 

Таблица 3. Встречаемость и относительное обилие бабочек в Финляндии. 

n_sq – число квадратов 10×10 км, в которых вид был встречен хотя бы один раз в 1991–2011 гг.;   a_oc – встречаемость (балл) ; n_i  – общее число зарегистрированных на маршрутах особей; a_ab – относительное обилие (балл).   Виды расположены в порядке возрастания a_oc, внутри классовых интервалов – по возрастанию n_i; в графе a_oc/ a_ab статус ряда видов изменен в соответствии с подобранными распределениями (рис. 2 и 3) переводом в следующий или предыдущий класс по a_oc и (или) a_ab. Номенклатура дана по каталогу чешуекрылых Финляндии (Checklist…).

Table 3. Species occurrence and relative abundance of the butterflies in Finland.

n_sq – number of 10×10 km squares, where each species was recorded at least once in 1991-2011; a_oc – occurrence of a species (point) ; n_i  – total records of the specimens; a_ab – relative abundance of a species (point). The species are classified in order of increasing a_oc and inside of each class according to increasing n_i; the status of some species in column a_oc/ a_ab was changed after the fitting frequency (Figs. 2 & 3) by transfer to the next or previous class a_oc or a_ab, or both. Nomenclature follows checklist of the Finnish Lepidoptera (Checklist…).

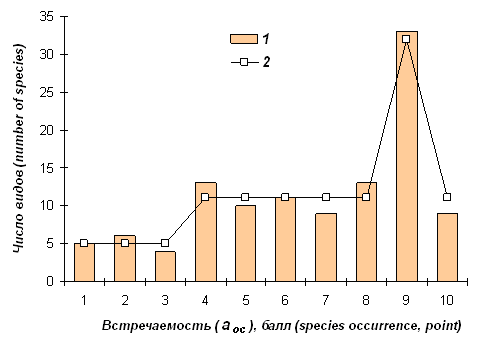
Распределение видов по встречаемости имеет относительно выровненную структуру (рис. 2). Отличия от равномерного распределения (χ² = 53.99, df = 9, p < 0.001) обусловлены, прежде всего, вкладом широко распространенных видов (a_oc = 9).  Уменьшение частоты этой варианты до теоретического уровня устраняет выявленную дифференциацию (χ² = 9.99, df = 9, p = 0.351). Вторая по значимости причина отличий – низкая доля спорадически встречающихся видов (a_oc = 1, 2, 3). Учет этих особенностей позволил подобрать модель, сводящую к минимуму исходную стохастичность, но при этом сохраняющую общую структуру данных. В результате подгонки эмпирических частот к выбранному распределению частот изменили статус 6 видов (табл. 3). Классу a_oc = 2 добавлена одна варианта, поскольку на верхней границе интервала оказались два вида с одинаковой встречаемостью (Maniola lycaon и Pyrgus andromedae).  

Рис. 2. Распределение видов по встречаемости. 1 –  эмпирические частоты;  2 – подобранная модель; отличия незначимы (χ² = 1.97, df = 4, p = 0.992)

Fig. 2. The distribution of species according to the occurrence. 1 – empirical frequency, 2 – selected model; the difference is non-significant (χ² = 1.97, df = 4, p = 0.992)

 

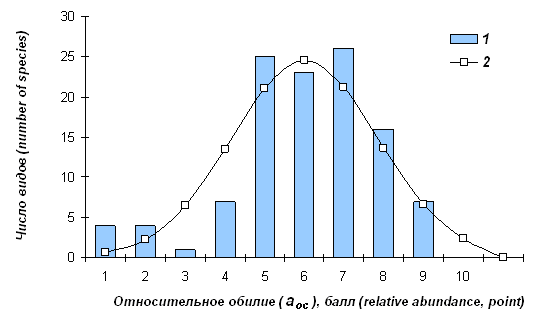
Дифференциация видов по обилию  вполне удовлетворительно описывается нормальным (логнормальным, учитывая имевшее место логарифмическое преобразование исходных значений на этапе шкалирования) распределением частот (рис. 3).  После внесения поправок 9 видов получили более высокие балльные оценки, 15 – более низкие, чем изначально было определено используемой шкалой (табл. 3).

Рис. 3. Распределение видов по относительному обилию. 1 –  эмпирические частоты;  2 – теоретические частоты (нормальное распределение); отличия незначимы (χ² = 5.89, df = 4, p = 0.208)

Fig. 2. The distribution of species according to relative abundance. 1 – empirical frequency, 2 – theoretical frequency (normal distribution); the difference is non-significant (χ² = 5.89, df = 4, p = 0.208)

Обсуждение

В рамках предложенного метода объединены преимущества двух традиционных подходов. Сохранив исходную 10-балльную двурядную систему (встречаемость / обилие), для дифференциации видов мы использовали количественные критерии. Балльные оценки на основе логарифмических шкал позволяют уменьшать диспропорции в массивах исходных данных, неизбежно возникающие вследствие отличий «качества» учетов, наличия «пробелов», ошибок наблюдений и получать обобщенные характеристики видов (табл. 3). Данный метод удобен для описания структуры населения беспозвоночных животных крупных географических объектов, начиная с уровня ландшафта, а баллы обилия могут быть использованы и для описания структуры сообществ.

Подгонка полученных распределений под выбранные модели призвана стабилизировать групповую принадлежность видов. Задача коррекции оценок обилия имеет более простое решение, поскольку закономерности распределения значимостей неплохо изучены (Коросов, 2007). Известно, что большие выборки организмов определенной таксономической группы, обитающих на территории с разнообразными биотопами, дают логнормальное распределение частот (Гиляров, 2007). Анализируемый материал не составляет исключения (рис. 2) и поэтому подгонка эмпирических частот, преследующая цель дать более адекватное описание генеральной совокупности, здесь вполне обоснована. Что касается встречаемости, то закономерности в распределении частот неясны. Вместе с тем это менее вариабельная характеристика, чем обилие. В большинстве беспозвоночные животные ведут оседлый образ жизни, встречаясь из года в год в одних и тех же местах. Процессы расселения даже у таких подвижных насекомых как бабочки,  обычно охватывают территории, по площади сопоставимые с исследованными квадратами (Горбач, Кабанен, 2009; Горбач и др., 2010). По этой причине полученные оценки вряд ли нуждаются в существенных поправках. Серьезные ошибки в определении статуса видов здесь могут возникать лишь вследствие использования бинарных значений (вид присутствует или отсутствует в списке из определенной точки). Точность оценок можно повысить введением формальных критериев, позволяющих удалять из базы данных выборки с неполными списками видов.

Рассмотренный пример показывает, что основу фауны дневных бабочек Финляндии составляют широко распространенные виды (Рис. 2), локальных видов немного.  Наиболее стабильны группы бабочек с относительным обилием a_ab > 4 (Рис. 3). Первые три класса слабо дифференцированы: добавление небольшого числа случайных величин может существенно изменять статус объектов. Сопоставление встречаемости и относительного обилия видов выявило в каждой из этих групп  две составляющие (табл. 3). Прежде всего, это виды, существенного дрейфа которых не предвидится. Для видов Boloria improba, Scolitantides vicrama, Pyrgus andromedae, Colias tyche, Plebeius glandon, Glaucopsyche arion и Boloria napaea на территории Финляндииуже давно обнаружены несколько локальных относительно многочисленных популяций. Все остальные бабочки, за исключением беляночки Leptidea reali, являются типичными мигрантами, статус которых может существенно варьировать во времени в зависимости от интенсивности потоков особей с сопредельных территорий (Pöyry et al., 2009). Это наиболее неустойчивый компонент рассматриваемых совокупностей. Например переливница Apatura ilia, принадлежащая к числу регулярно встречающихся видов, еще десять лет назад даже не числилась в списках дневных бабочек Финляндии. Беляночка L. reali, ранее не отличавшаяся от L. sinapis, не столь редка, как следует из имеющихся данных, и в дальнейшем, по-видимому, будет смещать свое расположение на обеих шкалах вправо.

Заключение или выводы

Рассмотренный метод балльных оценок представляет собой один из возможных вариантов дифференциации многовидового населения беспозвоночных животных исследуемой территории. Преимущество перед традиционными описаниями встречаемости и обилия видов в фаунистических работах состоит в формализации критериев для определения статуса видов. Основой служат объективные характеристики, полученные в результате учетов. Балльные оценки подвержены меньшей изменчивости от сезона к сезону, чем исходные количественные показатели, и поэтому больше подходят для описания структуры фауны. Их использование позволят уменьшить диспропорции исходных выборок, неизбежно возникающих при объединении материалов, поступающих в базы данных из многочисленных и не всегда равноценных источников. Как показывает рассмотренный пример с бабочками Финляндии, двурядная схема (встречаемость/обилие) устанавливает ясные критерии для различения среди редких форм локально распространенных оседлых видов и видов-мигрантов. Относительно многочисленные виды с низкой встречаемостью, как правило, наиболее уязвимы и должны рассматриваться в качестве первых кандидатов на включение в списки охраняемых животных.

Библиография